Advances in Chemical Engineering and Science
Vol.04 No.04(2014), Article ID:50864,9 pages
10.4236/aces.2014.44054
The Lattice Kinetic Monte Carlo Simulation of Boron Diffusion in SiGe
Yu-Wei Huang, Ren-Shiou Ke, Shyi-Long Lee*
Department of Chemistry and Biochemistry, University of National Chung-Cheng, Chia-Yi, Chia-Yi
Email: *chesll@ccu.edu.tw
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 July 2014; revised 26 August 2014; accepted 22 September 2014
ABSTRACT
The lattice kinetic Monte Carlo simulation (kMCS) was applied to study the boron diffusion in Si-SiGe beyond nanotechnology. Both the interstitialcy and kick-out mechanisms of boron diffusion were considered, including the effects of annealing temperatures, boron dopant concentrations, Ge compositions, and concentrations of Si self-interstitial defects (SiI). The effects on boron diffusion caused by single and double layer(s) of SiGe phase with different Ge contents and varying boron concentrations in double layers of SiGe phase were also simulated. The results show that boron diffusion in Si and between SiGe-Si both largely increase as the temperature or concentration of SiI increases, but the boron diffusion between SiGe-Si is much less than in Si. Increasing the Ge contents in SiGe alloy could retard boron diffusion heavily, while increasing the boron concentration on SiGe phase would enhance boron diffusion.
Keywords:
SiGe, Boron Diffusion, Kinetic Monte Carlo Simulation

1. Introduction
In situ heavily boron-doped Si1-xGex epitaxy that is thermally stable in source/drain regions is very essential for a p-type metal-oxide-semiconductor field effect transistor. As the Si-based device continue downscaling to sub-100 nm range, ultra shallow junctions for source/drain extension (SDE) could be required, therefore, the dopant diffusion in Si1-xGex plays an important role to form the ultra shallow pn junctions. It is known to boron atoms diffuse via self-interstitials or vacancies during epitaxy growth [1] , and could diffuse rapidly after thermal annealing arising from Si self-interstitial defects (SiI) introduction [2] -[4] , namely transient enhanced diffusion (TED), through combination of boron and self-interstitial defects (SiI). In order to reduce boron TED, lots of methods have been proposed, such as rapid thermal annealing (RTA) and impurity doping (introducing N or P into Si substrate) [5] -[7] . Hitherto, it has been proposed that boron diffusion could be retarded in compressive strained Si1-xGex alloys [8] -[12] . Boron diffusivity in strained as well as relaxed Si1-xGex alloys largely decreased at Ge content up to 40% but increased again at high Ge levels were also reported [13] -[15] . Bang et al. showed the boron diffusion reduced in Si1-xGex alloy by DFT calculation and they pointed out that the retarded B diffusion could be attributed to the following reasons: 1) the presence of Ge increases the migration energy of a Si self-interstitial defect then reduces the numbers of Si self-interstitials available for B diffusion; and 2) increases the migration energy of the B interstitial [16] .
The Boron diffusion between the source/drain and the n-well channel of p-type metal-oxide semiconductor (pMOS) which has drawn considerable attention is an important topic because owing to the electrical characteristics properties of n-type substrate could be degraded by boron diffusion., and then the efficiency of pMOS is reduced. In this study, the frameworks of two phases lattice kinetic Monte Carlo simulation (kMCS) were applied to characterize boron diffusion mechanisms between SiGe and Si. The boron atoms are put in a region of width of 54 nm in a lattice of 108 nm × 54 nm area for nano device applications. In the case of small lattice size, the concentration of SiI is very low in our lattice kMCS, and hard to be regarded as independent species to consider (i.e. it is hard to create “one” SiI in the simulation). In order to simulate the boron diffusion under this small size, hence, the “average” SiI, therefore, was applied in place of the “dot” SiI, the details were reported in Section 2. In addition to the effects of concentrations of SiI, boron concentration, Ge composition, and annealing temperature were all considered in our simulations. The simulation details were presented in Section 2. Results and discussion were reported in Section 3. Conclusions were drawn in Section 4.
2. Simulation Models
In order to simulate the boron diffusion between Si and SiGe, it is important to understand the basic diffusion mechanism. Up to now, The mechanisms of boron diffusion have been extensively studied. From the experimental or theoretical evidences, The Boron diffusion would follow two possible mechanisms, the interstitialcy and kick-out mechanisms [17] -[19] . The details of these two mechanisms are listed as
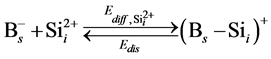 (1)
(1)
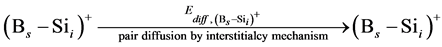 (2)
(2)
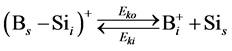 (3)
(3)
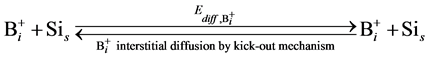 (4)
(4)
In the B-doped Si or SiGe, several different charge states of species can be found. To purify the problem, only the important charged species for boron diffusion are considered in our simulation. The pair between boron and self-interstitial Si defect plays an important role for boron diffusion. After forming the 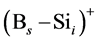 pair, the pair can diffuse through the interstitialcy mechanism or undergo kick-out to yield the interstitial boron that subsequently diffuse through the kick-out mechanism.
pair, the pair can diffuse through the interstitialcy mechanism or undergo kick-out to yield the interstitial boron that subsequently diffuse through the kick-out mechanism.
In this study, the lattice kinetic Monte Carlo simulation (kMCS) with Metropolis algorithm was performed to simulate the boron diffusion between Si and SiGe. The basic equation of Metropolis algorithm is shown as
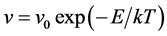 (5)
(5)
where the v is attempt frequency, v0 is collision frequency and E is reaction or diffusion activation energy. To apply the kMCS in the simulation of the boron diffusion, the collision frequency and activation energy for each reaction or diffusion path must be determined. Jung et al. had been reported the activation energies of various elementary steps for the boron diffusion [20] . In their works, the activation energies are evaluated by the statistical methods of maximum likelihood parameter estimation. By using the statistical method to average the experimental and computational results, the more confident parameter can be gained and used in our simulation. The exact collision frequencies are difficult to define, because it needs the information of heat distribution of phonon frequencies. Hence the approximate collision frequency, Debye frequency 6E12 s−1 is used in our study. For the association reaction of 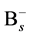 and
and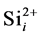 , although the activation energy barrier may exist, the opposite charges on the reactants and the negative free energy of formation for the complex give reasons to believe that the complex forms with no barrier. However the occurrence of association reaction of Bs− and Sii+2 must be through the diffusion of Si self-interstitial defect, the association activation energy can be regarded as the activation energy of Si self-interstitial defect diffusion.
, although the activation energy barrier may exist, the opposite charges on the reactants and the negative free energy of formation for the complex give reasons to believe that the complex forms with no barrier. However the occurrence of association reaction of Bs− and Sii+2 must be through the diffusion of Si self-interstitial defect, the association activation energy can be regarded as the activation energy of Si self-interstitial defect diffusion.
Some reports show that the effective range of association of 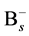 and
and 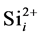 does not be limited in the nearest neighbor distance because the Columbic attraction between the species of opposite charges probably leads to increase the associative ability. The effective capture range can be extended to 1 nm comparing to the Si nearest neighbor distance 0.27 nm. Hence, the additional factor 3.7 (1 nm/0.27 nm) for the association of
does not be limited in the nearest neighbor distance because the Columbic attraction between the species of opposite charges probably leads to increase the associative ability. The effective capture range can be extended to 1 nm comparing to the Si nearest neighbor distance 0.27 nm. Hence, the additional factor 3.7 (1 nm/0.27 nm) for the association of 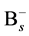 and
and  is included in the collision frequency.
is included in the collision frequency.
The effect of Si self-interstitial defect is large and cannot be ignored, because the diffusion of boron must be through the auxiliary of Si self-interstitial defect. Hence, in our simulation, the “average” Si self-interstitial defects instead of the “dot” Si self-interstitial defects. The concentration of Si self-interstitial defect for the perfect Si crystal is
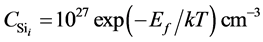 (6)
(6)
where the Ef is the formation energy of Sii.
Because the simulated lattice length is 0.27 nm, the equilibrium constant for Sii formation in the perfect Si crystal is
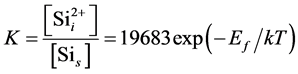 (7)
(7)
In order to include the effect of “average” Si self-interstitial defect in the simulation, the rate equation of association reaction of 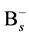 and
and 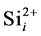 was considered and shown as
was considered and shown as
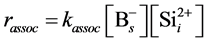
Because the activation energy of association reaction can determine by considering the diffusion of Si interstitial defect, the reaction constant kassoc can be expressed as
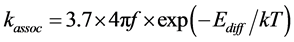
where f is the Debye frequency and Ediff is the activation energy of self-interstitial defect diffusion.
Combining the Equations (7)-(9), the rate equation can be written as
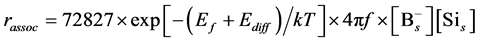
Hence the accept frequency for 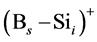
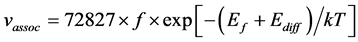
The concentration of Si self-interstitial defect is an important factor for boron diffusion. Here, the Si self-in- terstitial defect ratio, CI, with respect to the concentration of perfect Si crystal was defined and can be considered as
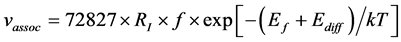
The diffusion ratio (RD) for boron is defined by Equation (13). The Nout is the number of boron atoms which diffuse out of original region (i.e. diffusion number of boron), Nboron is the number of total boron atoms.
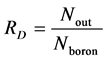
In the SiGe phase, the effect of Ge for boron diffusion was needed to consider. Many reports show that Ge atom could retard boron diffusion since Ge atom can trap Si self-interstitial defects then reducing the number of Si self-interstitial defects to form the Bs – Sii pair. [14] In the same time, the presence of Ge atom also increases the migration energy of boron interstitial to reduce boron diffusion. In our simulation for SiGe phase, the activation energies for boron diffusion in SiGe were tuned larger than in pure Si. For interstitialcy mechanism (i.e. B-I pair diffusion), the activation energy in SiGe phase is 0.77 eV larger than in Si phase by 0.10 eV. For kick-out mechanism, the activation energy is also increased from 1.05 eV (in Si phase) to 1.15 eV (in SiGe phase), then kick-in mechanism and Bi diffusion in SiGe phase are also increased about 0.05 eV than in Si phase. When the boron atom diffuses across different phases, such as from SiGe phase into Si phase, the activation energy of boron diffusion is the average activation energy of in SiGe phase and in Si phase, the equation can be shown as
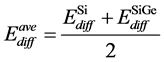
where 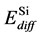
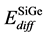
Because in the average SiGe phase cannot show the effect on different Ge contents in SiGe phase, so this effect was needed to consider in our simulation. If boron atom diffuses from or into SiGe grid, the activation energy of boron was increased as same as in the SiGe phase. The numbers of first-neighborhood of Ge were also needed to be considered, as the surrounding Ge also affected the boron diffusion [21] .
3. Results and Discussion
3.1. Boron Diffusion in Si Phase
First, the boron atoms are randomly distributed in a region of width of 54 nm in a lattice of 108 nm × 54 nm as shown in Figure 1(a), the phase I and phase II are Si phase. The boron concentration is 2E19 cm−3 in phase I and the diffusion time is 100 seconds in our simulation. In order to improve the accuracy of simulation and reduce the random error, 400 simulation runs were done for each condition to take the average. The effects of temperature and concentration of SiI on boron diffusion were considered.
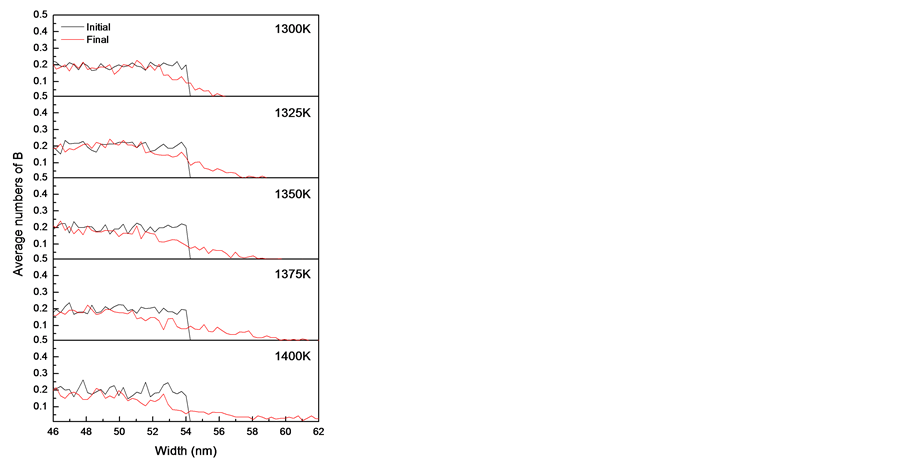
Figure 2(a) and Figure 2(b) show the boron diffusion profiles at different temperature from 1300 K to 1400 K and different concentrations of SiI from CI = 1 to CI = 5 at 1300 K, the solid line is the average of totally initial conditions and the dotted line is the average of totally final conditions. It can be found that the initial conditions are not dependent on the temperature or concentrations of SiI, but the final conditions are very different. The boron diffusion length can be to about 9 nm at 1400 K or 6 nm at high concentration of SiI as CI of 5. It also shows that the diffusion number and length of boron both increase when the temperature or concentration of SiI increases. The average diffusion ratio and length of boron in Si phase at boron concentration of 2E19 cm−3 with respect to different temperature and concentrations of SiI at 1300 K was collected in Table 1.
It can be found that the average diffusion length is strongly dependent on temperature. The concentrations of SiI was included in the simulation by controlling the accepted frequency of BI formation and listed in Equation (12), which the pre-exponential factor CI was tuned to decide the concentration of SiI. The results show that the enhancement of boron diffusion ratio is large when increasing the concentration of SiI. As the concentration of

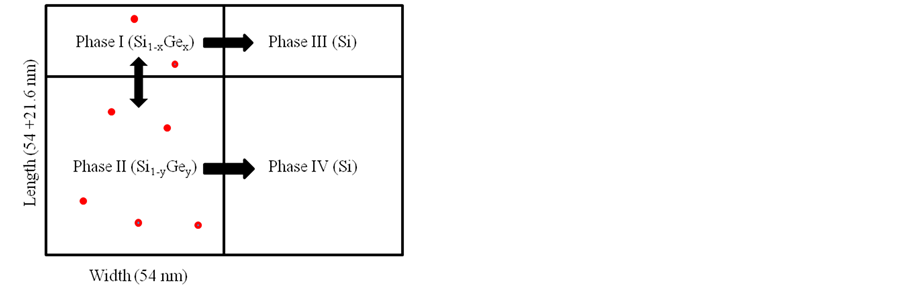
Figure 1. The simulation models for boron diffusion are drawn (a) between two phases and (b) from different configurations of SiGe to Si phase.

Figure 2. The boron diffusion profiles in pure Si phase are drawn with (a) different temperature and (b) different concentrations of Si self-interstitial defects at 1300K. (The black line is the initial condition and the red line is the final condition).
Table 1. The average diffusion ratio and length of boron under boron concentration = 2E19 cm−3 in Si and between SiGe and Si with respect to different temperature and concentrations of Si self-interstitial defects.
SiI increases, the values of average diffusion ratio are 0.94, 1.63, 1.58, 1.86 and 1.91% and the values of average diffusion length are 1.06, 1.51, 1.70, 1.98, and 2.22 nm with respect to CI = 1, 2, 3, 4 and 5 respectively. It again shows the average diffusion ratio and length both largely increase when the temperature or concentration of SiI increases. To compare the effect between the temperature and the concentration of SiI, it shows that the effect of temperature on the boron diffusion is larger than that of concentration of SiI.
3.2. Boron Diffusion between SiGe Phase and Si Phase
By changing the phase I in Figure 1(a) to SiGe phase, one can simulate the boron diffusion from SiGe phase into Si phase. The boron concentration = 2E19 cm−3 in phase I and the diffusion time is 100 seconds in our simulation. Again, the effects of temperature and concentration of SiI on boron diffusion were considered.
Figure 3(a) and Figure 3(b) show the boron diffusion profiles at different temperature from 1300 K to 1400 K.

Figure 3. The boron diffusion profiles between SiGe phase and Si phase are drawn with (a) different temperature (b) different concentration.
It can be found that the diffusion lengths of boron largely increase when the temperature increases. The average diffusion ratio and length of boron from SiGe phase into Si phase at concentration of boron = 2E19 cm3 with respect to different temperature and concentrations of SiI at 1300 K was collected in Table 1. As shown in Table 1, the average diffusion ratios increase from 0.15%, 0.94%, 1.17%, 1.83% to 2.36% and the average diffusion lengths also increase from 1.02, 1.50, 2.23, 2.68 to 3.70 nm with respect to 1300 K, 1325 K, 1350 K, 1375 K and 1400 K respectively. As the concentration of SiI increases from CI = 1 to CI = 5, and (b) different concentration of Si self-interstitial defects from 1.02 to 1.75 nm. Again, it shows that the effect of temperature on the boron diffusion is larger than that of at 1300K, the average diffusion ratio increases from 0.15% to 0.63% and the average diffusion length increases concentration of SiI.
Table 1 also summarizes the average diffusion ratio and length of boron between two phases with respect to different temperature and concentrations of SiI. The average diffusion ratio and length generally increase when the temperature or concentration of SiI increases. As can be seen from Table 1, it shows that the average diffusion ratio from SiGe phase into Si phase is the smallest. This can be rationalized as the boron atoms diffuse out from SiGe phase hardly but back to SiGe easily. To compare the boron diffusion in pure Si phase and between SiGe phase and Si phase, it shows that the average diffusion ratio from SiGe phase is smaller than that from pure Si phase, but the average diffusion length is strongly dependent on Phase II. The results show that the average diffusion lengths of boron which diffuses into Si phase or into SiGe are similar.
3.3. Boron Diffusion from SiGe Phase into Si Phase at Different Composition of Ge
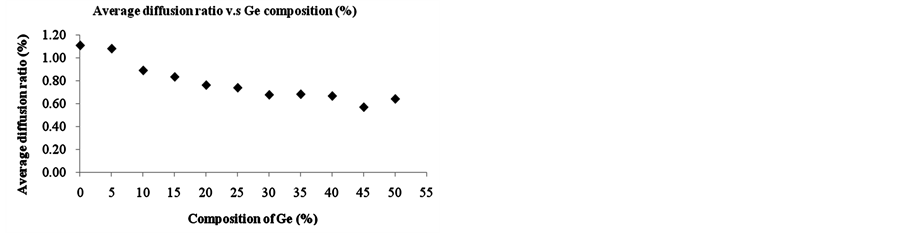
By varying the Ge content from 0% to 50% in SiGe phase of single layer in phase I as shown in Figure 1(a), one can study the effect of different SiGe configurations on boron diffusion. The diffusion time is 100 seconds and 1000 simulation runs were done for each condition to take the average. Figure 4 shows the average diffusion ratio and length of boron at different Ge composition from 0% to 50% under boron concentration of 2E19 cm−3 and 1300 K. As can be seen in Figure 4, the increase of Ge ratio is found to decrease the average diffusion ratio but do not effectively change the average diffusion length. Our simulation results show the increase of Ge content can retard the boron diffusion.
The effect on boron diffusion caused by double layers of SiGe phase with different composition of Ge as shown in Figure 1(b) was considered. As can be seen in Figure 1(b), the boron atoms could diffuse from phase I and II into phase III and IV, it also can exchange between phase I and II or phase III and IV. But the numbers
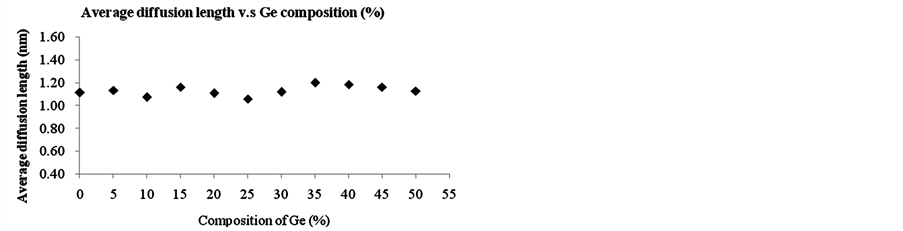
Figure 4. (a) The average diffusion ratio and (b) average diffusion length of boron at concentration of boron = 2E19 cm−3 from different composition of SiGe phase into Si phase under temperature at 1300 K.
of boron atoms which diffuse into phase III and IV were too low, so the exchange of boron atoms between phase III and IV were neglected that can be concluded the boron diffusion into phase III(IV) was all from phase I(II). 1000 simulation runs were done for each condition to take the average. Table 2 reports the average diffusion ratio and length of boron under boron concentration of 2E19 cm−3 and 1300 K at different combination of Ge composition on two layers of SiGe phase. As can be seen from Table 2, the average diffusion ratios decrease in homogenous SiGe phase when the Ge content increases. For SiGe configuration of Ge15% (top) + Ge30% (bottom), the average diffusion ratio was slightly reduced comparing with that for homogenous SiGe configuration of Ge26%. It also can be found that the exchange of boron atoms between phase I and phase II in the homogenous SiGe of Ge26% and Ge30% is nearly zero. But in nonhomogenous SiGe phase of Ge15% (top) + Ge30% (bottom), it has some boron atoms diffused from phase I into phase II since the Ge content between these two phases is different.
By changing the boron concentration, one can study the boron concentration effect on boron diffusion. Table 3 summarizes the average diffusion ratio and length for boron diffusion from SiGe phase into Si phase with different boron concentrations from 2E19, 4E19 to 8E19 cm−3 in top layer of Ge15% and from 1.5E19, 2E19 to 4E19 cm−3 in bottom layer of Ge30% on SiGe phase at 1300 K. As shown in Table 3, the increase of boron concentration is found to increase the total average diffusion number, from 0.41 to 0.89 with respect to homogenous boron concentration of 2E19 cm−3 and 4E19 cm−3, but do not effectively change the average diffusion length. It also can be found the exchange of boron atoms between phase I and phase II in homogenous boron concentration is smaller than in nonhomogeneous boron concentration. It can be concluded that the boron atoms would diffuse from high boron concentration to low boron concentration on double layers of SiGe phase.
By increasing the boron concentration from 2E19, 4E19 to 8E19 cm−3 in the top layer of SiGe phase and keeping the boron concentration at 2E19 cm−3 in the bottom layer of SiGe phase, the results show that the increase of boron concentration in top layer would increase the total average diffusion number from 0.41, 0.52 to 0.79, respectively. It can be found that the increase of total average diffusion number can be attributed to the increase of average diffusion number in phase III. Since the boron concentration in the top layer of SiGe phase increases twice from 2E19 cm−3 to 4E19 cm−3, the average diffusion numbers also increase about twice from 0.13 to 0.26 in phase III, but do not effectively change in phase IV. It also can be found the quantity of boron exchange between phase I and phase II largely increase from 0.02, 0.40 to 1.11 when the boron concentration increases in the top layer of SiGe phase.
By keeping the boron concentration at 4E19 cm−3 in the top layer of SiGe phase and changing the boron concentration from 1.5E19, 2E19 to 4E19 cm−3 in the bottom layer of SiGe phase, the results show the increase of B concentration in bottom layer would strongly increase the total average diffusion number from 0.47, 0.52 to 0.89, but the quantity of boron exchange between phase I and phase II is decreased from 0.50, 0.40 to 0.09, respectively. The decrease of boron exchange can be attributed to the boron concentration in bottom layer more and more close to the top layer. The increase of total average diffusion number can be contributed to the increase of average diffusion number in phase IV, as the boron concentration in the bottom layer of SiGe phase increases twice from 2E19 cm−3 to 4E19 cm−3, the average diffusion number also increases about twice from 0.26 to 0.62 in phase IV.
Table 4 reports the average diffusion ratio and length for boron diffusion from SiGe phase with boron con-
Table 2. The average diffusion ratio and length of boron under boron concentration = 2E19 cm−3 and 1300 K from different combination of Ge composition on SiGe phase into Si phase, the numbers in the parentheses are average diffusion number.
Table 3. The average diffusion ratio and length of boron from SiGe phase [Ge15%(top)+Ge30%(bottom)] to Si phase with different concentrations of boron at 1300 K, the numbers in the parentheses are average diffusion number.
Table 4. The average diffusion ratio and length of boron from SiGe phase [Ge16%(top)+Ge26%(bottom)] to Si phase with different temperature and different concentrations of Si self-interstitial defects at 1300 K, the numbers in the parentheses are average diffusion number.
centration = 4E19 cm−3 on top layer of Ge15% and boron concentration = 2E19 cm−3 on bottom layer of Ge30% to Si phase with respect to different temperature and concentrations of SiI at 1300 K. The diffusion time is 100 seconds and 400 simulation runs were done for each condition to take the average. When the temperature or concentrations of SiI increases, the average diffusion ratio of boron in phase III, phase IV and between phase I and phase II all increase, and the average diffusion length also increase largely.
4. Conclusion
First, the effects of temperature and concentration of SiI on boron diffusion in pure Si phase were considered. The results show the boron diffusion ratio and length both largely increase as the temperature or concentration of SiI increases. It also shows the effect of temperature on the boron diffusion is larger than that of concentration of SiI. For the boron diffusion from SiGe into Si phase, similar trends were found for the effects of temperature and concentration of SiI, but the boron diffusion largely decreases compared to that in pure Si. The results of boron diffusion from SiGe phase at different compositions of Ge into Si phase show that the increase of Ge content could effectively decrease the boron diffusion, but the diffusion length is nearly the same. The effect on boron diffusion caused by double layers of SiGe phase with different Ge contents was also simulated. The results show the boron diffusion in nonhomogenous SiGe phase is slightly smaller than in homogenous SiGe phase. By fixing the Ge content of 15% on top layer and 30% on bottom layer of SiGe phase and varying the boron concentration on top- or bottom-layer in SiGe phase, the results show that the boron diffusion increases as the total boron concentration increases, while the exchange of boron atoms between these two layers would increase as the difference of boron concentration increases.
Acknowledgments
Financial assistance from National Science Council, Taiwan is gratefully acknowledged. We are also grateful to the National Center for High-performance Computing for computer time and facilities.
References
- Fahey, P.M., Griffin, P.B. and Plummer, J.D. (1989) Point Defects and Dopant Diffusion in Silicon. Reviews of Modern Physics, 61, 289-384. http://dx.doi.org/10.1103/RevModPhys.61.289
- Michel, A.E., Rausch, W., Ronsheim, P.A. and Kastl, R.H. (1987) Rapid Annealing and the Anomalous Diffusion of Ion-Implanted Boron into Silicon. Applied Physics Letters, 50, 416-418. http://dx.doi.org/10.1063/1.98160
- Servidoli, M., Sourek, Z. and Solmi S. (1987) Some Aspects of Damage Annealing in Ion-Implanted Silicon: Discussion in Terms of Dopant Anomalous Diffusion. Journal of Applied Physics, 62, 1723-1728. http://dx.doi.org/10.1063/1.339600
- Pichler, P. and Stiebel, D. (2002) Current Status of Models for Transient Phenomena in Dopant Diffusion and Activation. Nuclear Instruments and Methods in Physics Research Section B, 186, 256-264. http://dx.doi.org/10.1016/S0168-583X(01)00947-8
- Fiory, A. (2002) T. Recent Developments in Rapid Thermal Processing. Journal of Electronic Materials, 31, 981-987. http://dx.doi.org/10.1016/S0168-583X(01)00947-8
- Solmi, S. and Bersani, M. (2000) Effects of Donor Concentration on Transient Enhanced Diffusion of Boron in Silicon. Journal of Applied Physics, 87, 3696-3700. http://dx.doi.org/10.1063/1.372402
- Tishkovskii, E.G., Obodnikov, V.I., Taskin, A.A., Feklistov, V. and Seryapin, V.G. (2000) Redistribution of Phosphorus Implanted into Silicon Doped Heavily with Boron. Semiconductors, 34, 629-633. http://dx.doi.org/10.1134/1.1188043
- Moriya, N., Feldman, L.C., Luftman, H.S., King, C.A., Bevk, J. and Freer, B. (1993) Boron Diffusion in Strained Si1−x Ge-x Epitaxial Layers. Physical Review Letters, 71, 883-886. http://dx.doi.org/10.1103/PhysRevLett.71.883
- Cowern, N.E.B., Zalm, P.C., van der Sluis, P., Gravesteijn, D.J. and de Boer, W.B. (1994) Diffusion in Strained SiGe. Physical Review Letters, 72, 2585-2588. http://dx.doi.org/10.1103/PhysRevLett.72.2585
- Kuo, P., Hoyt, J.L., Gibbons, J.F., Turner, J.E. and Lefforge, D. (1995) Effects of Strain on Boron Diffusion in Si and Si1−xGex. Applied Physics Letters, 66, 580-582. http://dx.doi.org/10.1063/1.114019
- Zangenberg, N.R., Fage-Pedersen, J., Hansen, J.L. and Larsen A.N. (2003) Boron and Phosphorus Diffusion in Strained and Relaxed Si and SiGe. Journal of Applied Physics, 94, 3883-3891. http://dx.doi.org/10.1063/1.1602564
- Wang, C.C., Sheu, Y.M., Liu, S., Duffy, R., Heringa, A., Cowern, N.E.B. and Griffin, P.B. (2005) Boron Diffusion in Strained and Strain-Relaxed SiGe. Materials Science and Engineering: B, 124-125, 39-44.
- Lever, R.F., Bonar, J.M. and Willoughby, A.F.W. (1998) Boron Diffusion across Silicon-Silicon Germanium Boundaries. Journal of Applied Physics, 83, 1988-1994. http://dx.doi.org/10.1063/1.366927
- Zangenberg, N.R., Fage-Pedersen, J., Hansen, J.L. and Larsen, A.N. (2001) Boron Diffusion in Strained and Relaxed Si1-xGex. Defect and Diffusion Forum, 194-199, 703.
- Uppal, S., Willoughby, A.F.W., Bonar, J.M., Evans, A.G.R., Cowern, N.E.B., Morris, R. and Dowsett, M.G. (2001) Ion-Implantation and Diffusion Behavior of Boron in Germanium. Physica B: Condensed Matter, 525, 308-310.
- Bang, J., Kang, J., Lee, W.J., Chang, K.J. and Kim, H. (2007) Chemical Bonding Effect of Ge Atoms on B Diffusion in Si. Physical Review B, 76, Article ID: 064118. http://dx.doi.org/10.1103/PhysRevB.76.064118
- Car, R., Kelly, R., Oshiyama, A. and Pantelides, S.T. (1985) Microscopic Theory of Impurity-Defect Reactions and Impurity Diffusion in Silicon. Physical Review Letters, 54, 360-363. http://dx.doi.org/10.1103/PhysRevLett.54.360
- Nichols, C.S., de Walle, C.G. and Pantelides, S.T. (1989) Mechanisms of Equilibrium and Non-Equilibrium Diffusion of Dopants in Silicon. Physical Review Letters, 62, 1049-1052. http://dx.doi.org/10.1103/PhysRevLett.62.1049
- Zhu, J., de la Rubia, T.D., Yang, L.H., Mailhiot, C. and Gilmer, G.H. (1996) Pseudopotential Calculations of B Diffusion and Pairing in Si. Physical Review B, 54, 4741-4747. http://dx.doi.org/10.1103/PhysRevB.54.4741
- Jung, M.Y.L., Gunawan, R., Braatz, R.D. and Seebauer, E.G. (2004) Pair Diffusion and Kick-Out: Contributions to Di- ffusion of Boron in Silicon. AIChE Journal, 50, 3248-3256. http://dx.doi.org/10.1002/aic.10220
- Bang, J., Kim, H., Kana, J., Lee, W.J. and Chang, K.J. (2007) Retardation of Boron Diffusion in SiGe Alloy. Physica B: Condensed Matter, 401-402, 196-199. http://dx.doi.org/10.1016/j.physb.2007.08.145
NOTES
*Corresponding author.