Received 15 May 2016; accepted 27 June 2016; published 30 June 2016

ABSTRACT

This paper proposes the combined Laplace-Adomian decomposition method (LADM) for solution two dimensional linear mixed integral equations of type Volterra-Fredholm with Hilbert kernel. Comparison of the obtained results with those obtained by the Toeplitz matrix method (TMM) demonstrates that the proposed technique is powerful and simple.

Keywords:

Singular Integral Equation, Linear Volterra-Fredholm Integral Equation, Adomian Decomposition Method, Hilbert Kernel

1. Introduction

The Volterra-Fredholm integral equation (V-FIE) arises from parabolic boundary value problems. The integral equations appear in many problems of physics and engineering. The Adomian decomposition method (ADM) was proposed by George Adomian in [1] [2] . A lot of examination work has been put as of late in applying this method to a wide range of ordinary differential equations, partial differential equations and integral equations, linear and nonlinear. Many authors discussed solutions of linear and nonlinear integral equations by utilizing different methods. What’s more, others interested singular integral equation.

We consider the linear (V-FIE) with singular kernel given by

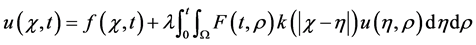(1)

There are several techniques that have been utilized to handle the integral Equation (1) in [3] - [5] ; a few techniques, for example, the projection method, time collocation method, the trapezoidal Nystrom method, and furthermore analytical or numerical techniques were utilized to treated this equation, but this techniques experienced troubles as far as computational work utilized. In [6] treated Maleknejad and Hadizadeh Equation (1) by using the Adomian decomposition method presented in [7] [8] introduced Wazwaz [9] the modified Adomian decomposition method for solving the Volterra-Fredholm integral equations.

In this work, we display numerical techniques to obtain numerical solution for linear mixed integral equation with Hilbert kernel. In Section 2, we talk about the existence and uniqueness of the solution. In Section 3, we discuss the Adomian decomposition method, as one of the well known technique and we note that the Adomian polynomials do not appear in this work because we handle linear problems. In Section 4, we present the Laplace Adomian decomposition method and apply this method to linear mixed integral equation with Hilbert kernel. In Sections 5 and 6, we display the Toeplitz matrix method.

2. The Existence and Uniqueness of the Solution [10]

Consider the integral Equation (1), the functions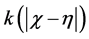, 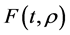and 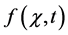are given and called the kernel of Fredholm integral term, Volterra integral term and the free term respectively and 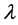is a real parameter (may be complex and has physical meaning). Also, Ω is the domain of integration with respect to position,

and the time t,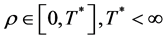. While 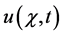is the unknown function to be determined in the space

.

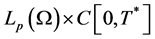In order to guarantee the existence of a unique solution of Equation (1) we assume through this work the following conditions:

(i) The kernel of position ,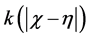

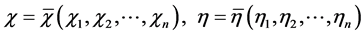
Satisfies the discontinuity condition

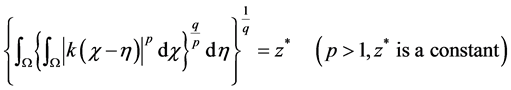
(ii) The kernel of time 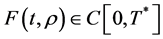satisfies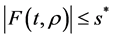, 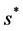is a constant,

.

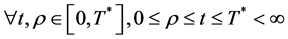(iii) The given function with its partial derivatives with respect to position and time t is conti-

nuous in the space, and its norm is defined as

(iv) The unknown function it behaves in this space, as the known function.

3. The Adomian Decomposition Method for Solving Volterra-Fredholm Integral Equation [11] [12]

Adomian decomposition method [1] [2] defines the unknown function by an infinite series

(2)

where the components will be determined recurrently and the nonlinear term decomposed into an infinite series of Adomian polynomials

The polynomials are produced for all kinds of nonlinearity so that depends just on, relies on upon and, and so on. The Adomian polynomial [1] [2] , , is given by,

(3)

Substituting Equation (2) into Equation (1) to get

(4)

The components are computed using the following recursive relations

(5)

(6)

4. The Combined Laplace-Adomian Decomposition Method Applied to Volterra-Fredholm Integral Equation with Hilbert Kernel [13] - [15]

We consider the kernel of Equation (1) take the form and applying the

Laplace transform to both sides of Equation (1) gives:

(7)

The linear term will be represented by the Adomian decomposition from Equation (2). Substituting Equation (2) into Equation (7) leads to

(8)

The Adomian decomposition method introduces the recursive relation

(9)

Applying the inverse Laplace transform to the first part of Equation (9) gives. Utilizing will empower us to evaluate, and so on. This will prompt the complete determination of the components of upon utilizing the second part of Equation (9). The series solution follows promptly after utilizing Equation (2). The obtained series solution may converge to an exact solution if such a solution exists.

5. The System of Fredholm Integral Equations (SFIEs) [16] [17]

In this part, a numerical technique is used, in the integral Equation (1) to obtain a system of linear integral equa-

tions with singular kernel, so we divide the interval, as

, where Then the formula (1) reduces to SFIEs of the second kind, in the form:

(10)

where

(11)

where is the error.

6. The Toeplitz Matrix Method (TMM) [17] - [19]

In this section, we apply (TMM) to obtain the numerical solution of the SFIEs (10) with singular kernel, each equation in this system can be written in a simplify form

(12)

The integral term in Equation (12) can be written as

(13)

We approximate the integral in the right hand side of Equation (13) by

(14)

where and are two arbitrary functions to be determined and is the estimate error which depends on and on the way that the coefficients are chosen. Putting in Equation (14) yields a set of two equations in terms of the two functions and. For choosing the values of, the error, in this case, must vanish.

We can, clearly solve the result set of two equations for and, to obtain

(15)

(16)

where

Hence, Equation (13) takes the form

(17)

where

The integral Equation (12), after putting, becomes

(18)

The formula (18) represents a linear system of algebraic equation , where u is a vector of elements, while is a matrix whose elements are given by

The matrix is a Toeplitz matrix of order, where.

The solution of the system (18) can be obtained in the form

The error term is determined from Equation (14) by letting , to get

7. Numerical Example

Example 1: Consider the linear mixed integral equation with Hilbert kernel

(19)

, the exact solution

we obtain Table 1.

8. Conclusions

In this paper, we applied (LADM) for solution two dimensional linear mixed integral equations of type Volterra- Fredholm with Hilbert kernel. Additionally, comparison was made with Toeplitz matrix method (TMM). It could be concluded that (LADM) was an effective technique and simple in finding very good solutions for these sorts of equations.

Using Maple 18, we obtain Table 1 and Figure 1 (since Figure 1 represents exact solution of u at t = 0.001, λ = 0.01, N = 20).

Acknowledgements

The authors would like to thank the King Abdulaziz city for science and technology.

Cite this paper

M. Salgueiro,P. González,T. F. Pena,J. C. Cabaleiro,Fatheah Ahmed Hendi,Manal Mohamed Al-Qarni, (2016) Comparison between Adomian’s Decomposition Method and Toeplitz Matrix Method for Solving Linear Mixed Integral Equation with Hilbert Kernel. American Journal of Computational Mathematics,06,177-183. doi: 10.4236/ajcm.2016.62019

References