Journal of Modern Physics
Vol.5 No.9(2014), Article ID:47405,8 pages
DOI:10.4236/jmp.2014.59094
A Quantum Battle of the Sexes in Noninertial Frame
Guofu Weng, Yang Yu
National Laboratory of Solid State Microstructures, School of Physics, Nanjing University, Nanjing, China
Email: physicswgf@126.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 April 2014; revised 1 May 2014; accepted 26 May 2014
ABSTRACT
We investigate the influence of the Unruh effect on the quantum Battle of the Sexes (BOF). We show that the acceleration of a noninertial frame greatly affects the payoffs of the players. In the case of Battle of the Sexes, the Nash Equilibra in the inertial frame may be equilibrium but in other games this conclusion may not be true anymore. Furthermore, we also show that the new Nash Equilibria of the game played in the noninertial frame and the probability distributions of the players in the new Nash Equilibria vary with the acceleration of moving player and the degree of entanglement in the initial state shared by the players.
Keywords:Quantum Game, Battle of the Sexes, Noninertial Frame

1. Introduction
The classical game theory emerged from the work of Von Neumann
[1] , and is applied to various fields, such as economics, social science,
medical science, biology and physics [2] -[4] . The relationship of the mathematical game theory and
the sources of quantum entanglement was first reported in 1999 by David Meyer [5] . In the same year, Eisert and his coworkers
proposed the quantization of nonzero sum games, and exploited the quantized scheme
into studying Prisoners’ Dilemma as a particular case of game
[6] . From then on the interested physicists have strenuously studied
the field that is taken to be a completely new direction in quantum correlations
and quantum computation processing. The original protocol for
 quantum games was introduced by Eisert et al. through quantum entanglement [6] [7] . In the seminal
paper of Meyer [5] and a number of subsequent
papers [8] -[13]
a particular two-parameter subset of SU(2) is introduced as the strategic space
for the players, which has mathematical simplicity and can solve some of the dilemmas
of classical game theory.
quantum games was introduced by Eisert et al. through quantum entanglement [6] [7] . In the seminal
paper of Meyer [5] and a number of subsequent
papers [8] -[13]
a particular two-parameter subset of SU(2) is introduced as the strategic space
for the players, which has mathematical simplicity and can solve some of the dilemmas
of classical game theory.
The quantum entanglement between spatially separated parties is the powerful source of processing the quantum information and the quantum computation. At present, the behavior of quantum entanglement in relativistic setup is under exploration [14] -[17] and some fascinating conclusions have been received. The undergoing studies in the noninertial frames show that entanglement between different modes of various field is degraded by the Unruh effect and the degree of entanglement asymptotically attains a non-vanishing minimum value in the infinite acceleration. Recently, the relativistic setup has been applied to the study of quantum game in noninertial frame and some interesting results have been gained in references [18] -[20] . On the quantum Prisoner’s Dilemma, for instance, S. Khan and M. K. Khan show that the payoff functions of the players are strongly affected by the acceleration of the noninertial frame and the symmetry of the game is disturbed in some extent [18] . Furthermore, quantum Stackelberg Duopoly in a Noninertial frame has been investigated and found that benefit of the initial state entanglement in the quantum form of the duopoly in the initial frame is adversely influenced by the acceleration of the non-stationary player [19] . Some theorists generalized the quantum game for three players, which one of the players stays stationary and the two others move with a uniform acceleration [21] .
Quantum game theorists have studied various specific games, such as Prisoner’s Dilemma, Battle of the Sexes, Cournot duopoly, Stackelberg Duopoly, and symmetric games like Rock-Paper-Scissors and so on [8] -[13] and [18] -[20] and [22] -[24] . Researchers intended to find solutions to those classical game in the background of quantum entanglement. Here, the word solution refers to a set of strategies that the rational players will surely play [22] .
In this Letter, we study the influence of the Unruh effect on the payoff functions of the players in the Battle of Sexes. We find that the game in noninertial frame can be transformed to classical game when the initial state is unentangled and both players remain stationary (i.e. acceleration is zero). We show that the expected payoffs of both players are relevant not only to the probability distributions of the players and the degree of entanglement of the initial state but they also vary with the acceleration of the moving player.
2. Quantum Version of Battle of the Sexes in Noninertial Frame
We exploit the concepts of quantum games in noninertial frame to study a two-person
static game of complete information, which is called the Battle of the Sexes. The
game is usually described as the following exposition: A women, Alice, and a man,
Bob, are planning to decide where to spend the Saturday night: Alice would prefer
to attend the Ballet, while Bob would like to watch the football match at the television.
They would prefer to stay together rather than far apart. We can represent the game
in a normal form by denoting by B (Ballet) and F (Football) the two pure strategies
which constitutes the common strategic space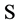 . The game is represented by the payoff matrix
in the table 1.
. The game is represented by the payoff matrix
in the table 1.
2.1. Quantization Scheme
In order to quantize the classical strategies B and F for player Alice, we assigned
two basic vectors
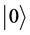 and
and
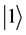 in a Hilbert space of two-level system to B and F, respectively
[6] . Similarly quantization scheme can be applied to the strategies of
player Bob and we obtain the quantum formation of the payoff table in the table 2.
in a Hilbert space of two-level system to B and F, respectively
[6] . Similarly quantization scheme can be applied to the strategies of
player Bob and we obtain the quantum formation of the payoff table in the table 2.
2.2. The Quantum Game in Noninertial Frame
We consider that Alice and Bob share an entangled initial state
![]() of the two qubits at a point in flat Minkowski spacetime. Alice and Bob possess
the first entry and the second entry in the ket, respectively. the unitary operator
of the two qubits at a point in flat Minkowski spacetime. Alice and Bob possess
the first entry and the second entry in the ket, respectively. the unitary operator
![]() is symmetric for fair games. The players perform their strategic moves as local
unitary operators
is symmetric for fair games. The players perform their strategic moves as local
unitary operators
![]() belonging to a full space of SU(2) strategies, which is a set of three-parameter
strategies:
belonging to a full space of SU(2) strategies, which is a set of three-parameter
strategies:
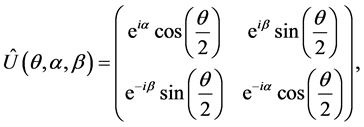 (1)
(1)
Table 1. Payoff matrix for the classical Battle of Sexes. The first entry in a pair of numbers denotes the payoff of Alice and the second entry stand for Bob’s payoff.
Table 2. The quantization scheme by the Eisert protocol:
classical pure strategies B (Ballet) and F (Football) correspond to the quantum
pure strategies
![]() and
and![]() , respectively.
, respectively.
where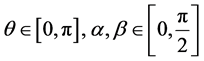 .
.
With classical strategic moves,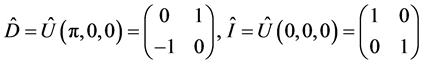 .
.
The unitary operator
![]() is an entangling operator and then is given by
is an entangling operator and then is given by
 (2)
(2)
where
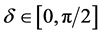 and is a measure of the degree of entanglement in the initial state. The initial
state is maximally entangled for the upper limit of
and is a measure of the degree of entanglement in the initial state. The initial
state is maximally entangled for the upper limit of
![]() and has no entanglement for the lower limit of
and has no entanglement for the lower limit of![]() .
.
The entangling operators
![]() must be known to both players for the knowledge of the degree of the entanglement
in the initial state. After the application of the entangling operator, the state
of the game evolves to
must be known to both players for the knowledge of the degree of the entanglement
in the initial state. After the application of the entangling operator, the state
of the game evolves to
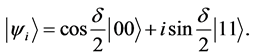 (3)
(3)
We assume that Alice stays stationary and Bob moves with a uniform acceleration. Each player possesses a device which is sensitive only to a single mode in their respective regions. From the accelerated player Bob’s frame, the Minkowski vacuum state is given by a two-mode squeezed state,
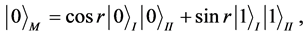 (4)
(4)
where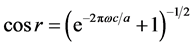 . The parameter
. The parameter
![]() is the dimensionless parameter, which
is the dimensionless parameter, which
![]() when
when
![]()
and
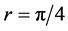 when
when![]() . The constants
. The constants![]() ,
,
![]() , and
, and![]() , in the above equation stand, respectively,
for the Dirac particle's frequency, light speed in vacuum and Bob’s acceleration.
In the Equation (4),the subscripts I and II of the kets represent the Rindler modes
in the region I and II, respectively, in the Rindler spacetime diagram Figure 1. The Equation (4) represents that the noninertial
observer that moves with a constant acceleration in region I observes a thermal
state instead of the vacuum state, which is called Unruh effect
[25] [26] .
, in the above equation stand, respectively,
for the Dirac particle's frequency, light speed in vacuum and Bob’s acceleration.
In the Equation (4),the subscripts I and II of the kets represent the Rindler modes
in the region I and II, respectively, in the Rindler spacetime diagram Figure 1. The Equation (4) represents that the noninertial
observer that moves with a constant acceleration in region I observes a thermal
state instead of the vacuum state, which is called Unruh effect
[25] [26] .
The excited state in Minkowski spacetime is relevant to Rindler modes as follows:
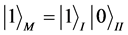 (5)
(5)
In terms of Minkowski mode for Alice and Rindler modes for Bob, the entangled initial state of Equation (3) by exploiting Equations (4) and (5) evolves
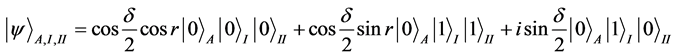 (6)
(6)
The corresponding mixed density matrix in the entangled initial state in Equation (6) is defined as
![]() (7)
(7)

Figure 1.
Rindler spacetime diagram: The uniformly accelerated observer Bob (B) moves on a
hyperbola with constant acceleration a in the region I and is causally disconnected
from the region II which a fictitious observer anti-Bob
 moves on.
moves on.
A uniformly accelerated observer (Bob) in Rindler region I is causally disconnected from the other region at the opposite side Figure 1, therefore, we must take trace over all the mode in region II. After the trace eperation, the density matrix is expressed as
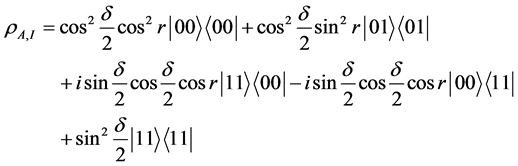 , (8)
, (8)
Note that the subscripts of the kets and bras have been dropped for simplicity. The density matrix can also be written as the following matrix:
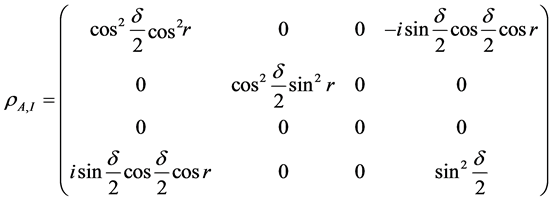 (9)
(9)
In the quantum Battle of the Sexes, each player has two possible strategies , the identity operator, and
, the identity operator, and![]() , the inversion operator or the Pauli’s bit-flip
operator. Let
, the inversion operator or the Pauli’s bit-flip
operator. Let
![]() and
and
![]() represent the probabilities of
represent the probabilities of
 and
and
![]() that Alice applies. Similarly,
that Alice applies. Similarly,
![]() and
and
![]() are the probabilities that Bob applies the identity operator and inversion operator,
respectively. After the players take their strategic moves, the final density matrix
evolves to
are the probabilities that Bob applies the identity operator and inversion operator,
respectively. After the players take their strategic moves, the final density matrix
evolves to
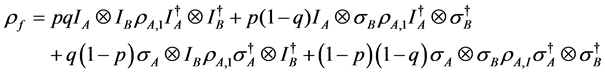 (10)
(10)
The payoff operators for Alice and Bob can be written as
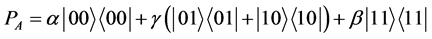 (11)
(11)
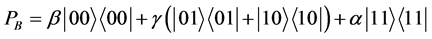 (12)
(12)
The payoff functions for Alice and Bob in the Battle of the Sexes respectively, are
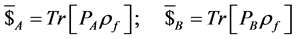 (13)
(13)
For the sake of convenience, the following variables can be defined:
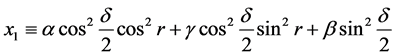 (14)
(14)
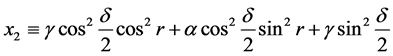 (15)
(15)
 (16)
(16)
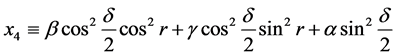 (17)
(17)
By using the above variables, the payoff functions in Equation (13) can be expressed in the following succinct way:
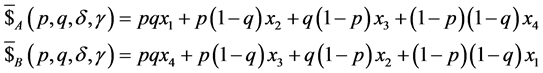 (18)
(18)
The payoff functions in Equation (18) show the expected gains of both players depend
on not only the probability distributions
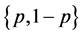 and
and
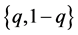 for Alice and Bob respectively, but also on the degree of entanglement
for Alice and Bob respectively, but also on the degree of entanglement
![]() and dimensionless acceleration parameter
and dimensionless acceleration parameter![]() . Furthermore, even in the case of unentangled initial
state (i.e.
. Furthermore, even in the case of unentangled initial
state (i.e.![]() ), the expected payoff functions depend on the probability
distributions of both players and as well vary with the the acceleration
), the expected payoff functions depend on the probability
distributions of both players and as well vary with the the acceleration
![]() of Bob.
of Bob.
Before we continue, let us first find some relationships about the variables defined in Equations (14)-(17):
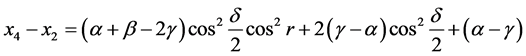 (19)
(19)
The value of
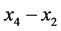 is not always positive. It could be nonnegative for some domains of
is not always positive. It could be nonnegative for some domains of
![]() and
and
![]() since
since
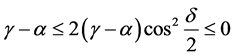 is true for the fact that
is true for the fact that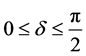 . For instance
. For instance
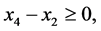 when
when
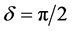 and
and
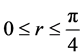 .
.
For the same sake, we can obtain the following inequalities:
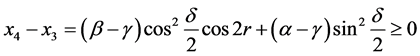 (20)
(20)
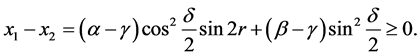 (21)
(21)
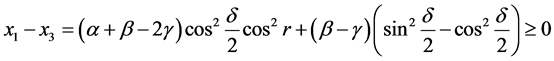 (22)
(22)
For the definite degree of entanglement
![]() and the acceleration of Bob, the expected payoff functions can be rewritten as follows:
and the acceleration of Bob, the expected payoff functions can be rewritten as follows:
![]() (23)
(23)
Nash Equilibria can be found by imposing the two coupled inequalities:
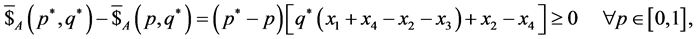 (24)
(24)
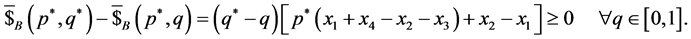 (25)
(25)
3. Results and Analysis
When two factors in both inequalities are both the same sign, we can get the Nash Equilibrium. There are three possibilities:
Case 1.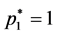 ,
,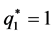 . In such a case both Alice and Bob play
the pure strategy B (Ballet). their expected payoff functions are
. In such a case both Alice and Bob play
the pure strategy B (Ballet). their expected payoff functions are
![]() and
and![]() , and by employing the in equalities (20) and (22) the following
inequalities hold:
, and by employing the in equalities (20) and (22) the following
inequalities hold:
![]() (26)
(26)
![]() (27)
(27)
The payoff functions in Nash Equilibriua are relevant to the degree of entanglement
of the initial state and the dimensionless acceleration parameter![]() . In inertial frame, the parameter
. In inertial frame, the parameter![]() , the payoffs of both players coincide when
the initial state is in maximally entangled. In this particular situation, the gains
of both players are
, the payoffs of both players coincide when
the initial state is in maximally entangled. In this particular situation, the gains
of both players are
![]() respectively. In the noninertial frame, the payoff function,
taking the gain of Alice for instance, is strongly influenced by the acceleration
parameter
respectively. In the noninertial frame, the payoff function,
taking the gain of Alice for instance, is strongly influenced by the acceleration
parameter
![]() such that the gain of Alice is given by
such that the gain of Alice is given by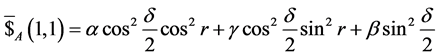 , which becomes
, which becomes
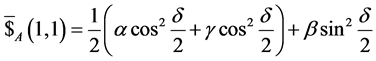 when player Bob is assumed to move in an infinite acceleration
corresponding to the parameter
when player Bob is assumed to move in an infinite acceleration
corresponding to the parameter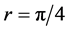 .
.
Case 2.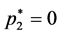 ,
,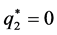 . In this case both Alice and Bob play
the another pure strategy F (Football). Their expected payoff functions are reversed
with respect to the previous case:
. In this case both Alice and Bob play
the another pure strategy F (Football). Their expected payoff functions are reversed
with respect to the previous case:
![]() and
and![]() .
.
Meanwhile, by the equation (19) we get following truth:
The payoff function of Alice
![]() (28)
(28)
is not always nonnegative for the nonpositive-definite value of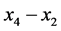 . In such a case this pure strategy is not
the Nash Equilibrium when the value of
. In such a case this pure strategy is not
the Nash Equilibrium when the value of
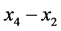 is negative. The new Nash equilibria could arise when
is negative. The new Nash equilibria could arise when
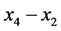 is positive by choosing the degree of entanglement in the initial state and the
acceleration of Bob.
is positive by choosing the degree of entanglement in the initial state and the
acceleration of Bob.
By inequality (21) we get the following inequality for the payoff function of Bob:
![]() (29)
(29)
In the inertial frame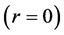 , the payoff functions are
, the payoff functions are
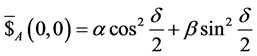 and
and
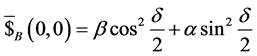 , respectively. If two players share an unentangled initial
state
, respectively. If two players share an unentangled initial
state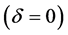 , the gains of the players in noninertial frame are
, the gains of the players in noninertial frame are
![]() and
and![]() , which are relevant to the dimensionless acceleration parameter
, which are relevant to the dimensionless acceleration parameter![]() .
.
Case 3. When the probabilities
![]() and
and
![]() are less than one but greater than zero, two of the factors in inequalities (24)
and (25) should be reasonable to be zero. Hence, we can solve the probabilities:
are less than one but greater than zero, two of the factors in inequalities (24)
and (25) should be reasonable to be zero. Hence, we can solve the probabilities:
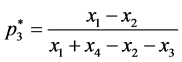 and
and
which correspond to the gains of both Alice and Bob coincide:
 (30)
(30)
The new Nash Equilibria are relevant to acceleration of Bob and degree of entanglement
in the initial state for the value of . When the value of
. When the value of
 is negative, the probability distribution of Bob is meaningless and it is so far
from the purpose that we could get new Nash Equilibrium.
is negative, the probability distribution of Bob is meaningless and it is so far
from the purpose that we could get new Nash Equilibrium.
In the case of unentangled initial state (i.e.![]() ), the equations (14)-(17) are reduced into
the following equations:
), the equations (14)-(17) are reduced into
the following equations:
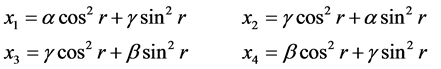 (31)
(31)
By using these equations, we can receive that
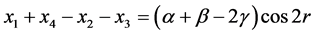 and
and
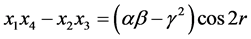 , by which the gains of players are obtained:
, by which the gains of players are obtained:
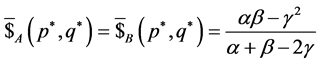 .
.
4. Discussions and Conclusions
As we can find from Eqautions (14)-(17) that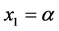 ,
,
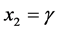 ,
,
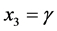 , and
, and
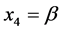 when the initial state is unentangled and both Alice and Bob are in the inertial
frame (i.e.
when the initial state is unentangled and both Alice and Bob are in the inertial
frame (i.e.![]() ). In such case, the payoff functions for players
correspond to the classical game and their expected payoffs are:
). In such case, the payoff functions for players
correspond to the classical game and their expected payoffs are:
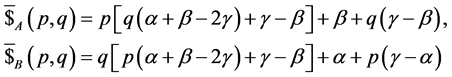 (32)
(32)
In this classical mixed strategies, three Nash Equilibria can be found [22] : 1) probability distribution (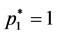 ,
,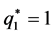 ) corresponds to pure strategy that
both Alice and Bob choose to play B. Their expected payoff functions are
) corresponds to pure strategy that
both Alice and Bob choose to play B. Their expected payoff functions are
![]() and
and![]() . 2) Strategies
. 2) Strategies
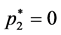 and
and
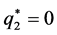 correspond to pure strategy, both Alice and Bob play F, and expected payoffs are
correspond to pure strategy, both Alice and Bob play F, and expected payoffs are
![]() and
and![]() . 3)
. 3)
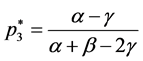 and
and
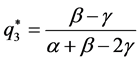 , which are correctly larger than zero and less than one,
correspond to a Nash Equilibrium for which the payoffs of both players coincide:
, which are correctly larger than zero and less than one,
correspond to a Nash Equilibrium for which the payoffs of both players coincide: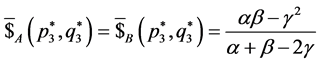 .
.
In a summary, we have shown that payoff functions are strongly influenced by the acceleration of moving player Bob in the noninertial frame. Payoff functions are affected by Unruh effect in the quantum Battle of the Sexes in noninertial frame. In the case of Battle of Sexes, the Nash Equilibria in inertial frame are still equilibria in the corresponding noninertial frame but the payoffs of both Alice and Bob are relevant to both degree of entanglement in the players’ initial state and the acceleration parameter. In the case of probability distribution
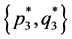 , it is a new Nash Equilibrium for the probability distributions
of both play are related to the degree of entanglement and acceleration parameter,
which can be backward induced to the inertial situation when we suppose the dimensionless
accelerating parameter
, it is a new Nash Equilibrium for the probability distributions
of both play are related to the degree of entanglement and acceleration parameter,
which can be backward induced to the inertial situation when we suppose the dimensionless
accelerating parameter![]() . In the limit of infinite acceleration, we find
that the payoff functions at the Nash Equilibria would be irrelevant to the acceleration
but only depend on the entanglement.
. In the limit of infinite acceleration, we find
that the payoff functions at the Nash Equilibria would be irrelevant to the acceleration
but only depend on the entanglement.
Acknowledgements
This work is supported by the National Key Projects for Basic Researches of China (No. 2011CB922104, 2011CBA00200), by the National Natural Science Foundation of China (No. 91021003, 11274156), the Natural Science Foundation of Jiangsu Province(No. BK2010012), and PAPD.
References
- von Neumann, J. (1951) Applied Mathematical Series, 3, 36-38.
- von Neumann, J. and Morgenstern, O. (1944) Theory of Games and Economic Behavior. Princeton University Press, Princeton.
- Piotrowski, E.W. and Sladkowski, J. (2002) Physica A: Statistical Mechanics and Its Applications, 312, 208-216.
- Baaquie, B.E. (2001) Physics Review E, 64, Article ID: 016121. http://dx.doi.org/10.1103/PhysRevE.64.016121
- Meyer, D.A. (1999) Physics Review Letter, 82, 1052-1055. http://dx.doi.org/10.1103/PhysRevLett.82.1052
- Eiset, J., Wilkens, M. and Lewenstein, M. (1999) Physics Review Letter, 83, 3077-3080. http://dx.doi.org/10.1103/PhysRevLett.83.3077
- Eisert, J. and Wilkins, M. (2000) Journal of Modern Optics, 47, 2543-2556. http://dx.doi.org/10.1080/09500340008232180
- Iqbal, A. and Toor, A.H. (2001) Physics Letter A, 280, 249-256. http://dx.doi.org/10.1016/S0375-9601(01)00082-2
- Du, J., Li, H., Xu, X., Shi, M., Wu, J. and Han, R. (2002) Physics Review Letter, 88, Article ID: 1379021. http://dx.doi.org/10.1103/PhysRevLett.88.137902
- Chen, L.K., Ang, H., Kiang, D., Kwek, L.C. and Lo, C.F. (2003) Physics Letter A, 316, 317-323. http://dx.doi.org/10.1016/S0375-9601(03)01175-7
- Ozdemir, S.K., Shimamura, J. and Imoto, N. (2004) Physics Letter A, 325, 104-111. http://dx.doi.org/10.1016/j.physleta.2004.03.042
- Ozdemir, S.K., Shimamura, J., Morikoshi, F. and Imoto, N. (2004) Physics Letter A, 333, 218-231. http://dx.doi.org/10.1016/j.physleta.2004.10.055
- Alonso-Sanz, R. (2012) Proceedings of the Royal Society A, 468, 3370-3383. http://dx.doi.org/10.1098/rspa.2012.0161
- Alsing, P.M., Fuentes-Schuller, I., Mann, R.B. and Tessier, T.E. (2006) Physics Review A, 74, Article ID: 032326. http://dx.doi.org/10.1103/PhysRevA.74.032326
- Terashima, H. and Ueda, M. (2003) International Journal of Quantum Information, 1, 93. http://dx.doi.org/10.1142/S0219749903000061
- Pan, Q. and Jing, J. (2008) Physics Review A, 77, Article ID: 024302. http://dx.doi.org/10.1103/PhysRevA.77.024302
- Fuentes-Schuller, I. and Mann, R.B. (2005) Physics Review Letter, 95, Article ID: 120404. http://dx.doi.org/10.1103/PhysRevLett.95.120404
- Khan, S. and Khan, M.K. (2011) Journal of Physics A: Mathematical and Theoretical, 44, Article ID: 355302. http://dx.doi.org/10.1088/1751-8113/44/35/355302
- Khan, S. and Khan, M.K. (2011) Chinese Physics Letters, 28, Article ID: 070202. http://dx.doi.org/10.1088/0256-307X/28/7/070202
- Khan, S. and Khan, M.K. (2013) Quantum Information Process, 12, 1351-1353.http://dx.doi.org/10.1007/s11128-012-0469-5
- Goudarzi, H. and Beyrami, S. (2012) Journal of Physics A: Mathematical and Theoretical, 45, Article ID: 225301.http://dx.doi.org/10.1088/1751-8113/45/22/225301
- Marinatto, L. and Weber, T. (2000) Physics Letter A, 272, 291-303. http://dx.doi.org/10.1016/S0375-9601(00)00441-2
- Iqbal, A. and Toor, A.H. (2004) Communications in Theoretical Physics, 42, 335-338.
- Iqbal, A. and Toor, A.H. (2002) Physics Review A, 65, Article ID: 022306. http://dx.doi.org/10.1103/PhysRevA.65.022306
- Davies, P.C.W. (1975) Journal of Physics A: Mathematical and General, 8, 609-616. http://dx.doi.org/10.1088/0305-4470/8/4/022
- Unruh, W.G. (1976) Physics Review D, 14, 870-892. http://dx.doi.org/10.1103/PhysRevD.14.870


