Applied Mathematics
Vol.07 No.03(2016), Article ID:64064,9 pages
10.4236/am.2016.73027
Cryptographic Schemes Based on Elliptic Curves over the Ring 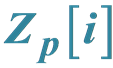
Manoj Kumar, Pratik Gupta
Department of Mathematics and Statistics, Gurukula Kangri Vishwavidyalaya, Haridwar (Uttrakhand), India
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).



Received 9 January 2016; accepted 26 February 2016; published 29 February 2016
ABSTRACT
Elliptic Curve Cryptography recently gained a lot of attention in industry. The principal attraction of ECC compared to RSA is that it offers equal security for a smaller key size. The present paper in- cludes the study of two elliptic curve  and
and 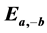 defined over the ring
defined over the ring 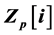 where
where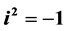 . After showing isomorphism between
. After showing isomorphism between 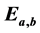 and
and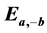 , we define a composition operation (in the form of a mapping) on their union set. Then we have discussed our proposed cryptographic schemes based on the elliptic curve
, we define a composition operation (in the form of a mapping) on their union set. Then we have discussed our proposed cryptographic schemes based on the elliptic curve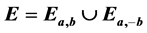 . We also illustrate the coding of points over E, secret key exchange and encryption/decryption methods based on above said elliptic curve. Since our proposed schemes are based on elliptic curve of the particular type, therefore the proposed schemes provides a highest strength-per-bit of any cryptosystem known today with smaller key size resulting in faster computations, lower power assumption and memory. Another advantage is that authentication protocols based on ECC are secure enough even if a small key size is used.
. We also illustrate the coding of points over E, secret key exchange and encryption/decryption methods based on above said elliptic curve. Since our proposed schemes are based on elliptic curve of the particular type, therefore the proposed schemes provides a highest strength-per-bit of any cryptosystem known today with smaller key size resulting in faster computations, lower power assumption and memory. Another advantage is that authentication protocols based on ECC are secure enough even if a small key size is used.
Keywords:
Elliptic Curve, Ring, Finite Field, Isomorphism, Cardinality, Encryption/Decryption

1. Introduction
Elliptic curve cryptography has been an active area of research since 1985 when Koblitz (Ref. [1] ) and Miller (Ref. [2] ) independently suggested using elliptic curves for public-key cryptography. A lot of work has been done on elliptic curve cryptography (Ref. [3] -[7] ). Because elliptic curve cryptography offers the same level of security as compared to RSA with considerably shorter keys, it has replaced traditional public key cryptosystems, especially, in environments where short keys are important. Public-key cryptosystems are computationally demanding and, hence, the fact that elliptic curve cryptography has been shown to be faster than traditional public-key cryptosystems is of great importance. Elliptic Curve Cryptographic (ECC) schemes are public-key mechanisms that provide the same functionality as RSA schemes. However, their security is based on the hardness of a different problem, namely the Elliptic Curve Discrete Logarithmic Problem (ECDLP). Most of the products and standards that use public-key cryptography for encryption and digital signatures use RSA schemes. The competing system to RSA is an elliptic curve cryptography. The principal attraction of elliptic curve cryptography compared to RSA is that it offers equal security for a smaller key-size.
2. Auxiliary Result
In this section first we discuss some essential arithmetic of elliptic curves, and then we mention some auxiliary results which are necessary to prove the main result. Although a lot of literature exist on arithmetic of elliptic curves (Ref. [8] -[11] ), a simple and easier arithmetic of elliptic curves are given by the following (Ref. [10] ):
An elliptic curve 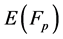 over a finite field
over a finite field 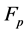 is defined by the parameters
is defined by the parameters  (a and b satisfy the relation
(a and b satisfy the relation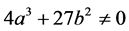 ), consists of the set of points
), consists of the set of points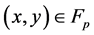 , satisfying the equation
, satisfying the equation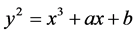 . The set of points on
. The set of points on 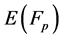 also include point O, which is the point at infinity and which is the identity element under addition. Actually elliptic curve are not ellipse. They are so called because they are described by cubic equation similar to those are used for calculating the circumference of an ellipse.
also include point O, which is the point at infinity and which is the identity element under addition. Actually elliptic curve are not ellipse. They are so called because they are described by cubic equation similar to those are used for calculating the circumference of an ellipse.
The Addition operation is defined over 


If



If 





Let

where

Now we discuss the auxiliary result of this section. For a prime number p, let 


Lemma 2.1. (Ref. [12] ) An element 


Proof. Let 



which implies 


In (1) take the conjugate

Multiply (1) and (2), we get
We deduce


Lemma 2.2. (Ref. [13] [14] ) Let p be a prime number. Then 

Proof. Assume that 



invertible. By Lemma 2.1, we have



















We deduce that 
Theorem 2.3. For two isomorphic abelian groups 



such that
where f is the isomorphism between 


identity element e and all elements in E are invertible.
Proof. It is clear that 
To show that e is the identity element with respect to binary operation
Let x in E. If 
because 

Else
because 


We have 

Let

If 
If 
If 

3. Elliptic Curve over the Field
Let 



where O is the point at infinity.
Corollary 3.1. If 

Proof. Let

This implies that

which is a contradiction.
Hence

4. Main Result
Theorem 4.1. Let f be a mapping from 


Then f is a bijection.
Proof. First we show that f is well defined.
Let 



Hence f is well defined.
f is one-one. Let 
This implies that 
So,
Hence, f is one-one.
f is onto. Let

This implies that 

Thus, f is onto.
f is homomorphism. Let 
Case I. When
As we know that addition of two different points 

where 
So we have
where 
Again
where 

It is obvious that 


Therefore

Case II. When 
where 

Again
where 

It is evident that 


Therefore,
Case III. When 
We have
and
Thus
Therefore, in either case f is an homomorphism. Hence f is a bijection.
Corollary 4.2. For two isomorphic abelian groups 



such that
where f is the isomorphism between 


Proof. Keeping in view the result of theorem-2.3, corollary-2.4, and theorem-3.1, it is evident that 
Corollary 4.3. If 


Proof. Since 

Now,
This implies that
Therefore,

5. Cryptographic Applications
In this section we shall illustrate our proposed methods for coding of points on Elliptic Curve, then exchange of secret key and finally use them for encryption/decryption.
5.1. Coding of Element on Elliptic Curve
It is described with the help of illustration 5.1 and illustration 5.2.
Illustration 5.1. For 


Since, 
Therefore

and

Coding of element 
Let


Illustration 5.2. For 


Let


The above scheme helps us to encrypt and decrypt any message of any length.
5.2. Exchange of Secret Key
1) For a publically integer p, and an elliptic curve 

2) P generates a subgroup say 
Now, key exchange between Alice and Bob can be described as follows
3) Alice chooses a random number

4) Bob chooses a random number

5) Alice computes
6) Bob computes
7) Alice and Bob are agree with a point

Remark. With the secret key 
Illustration 5.3. Let 
are two elliptic curve defined over the same field 



1) Alice chooses a random number

2) Bob chooses a random number 

3) Alice computes
4) Bob computes
5) Alice and Bob are agree with a point

5.3. ECC Key Generation Phase
Now, exchange of secret key involves the following steps:
1) Encode the message m on the point
2) Choose a random number k, compute 

3) Public key is
4) Private key is
5.4. ECC Encryption Phase
To encrypt


5.5. ECC Decryption Phase
Decryption of the message 




This operation is shown in Figure 2.
Illustration 5.4. The
Figure 1. The encryption operation.
Figure 2. The decryption operation.
are two elliptic curves defined over the same field 



Alice’s message is the point
Bob has chosen his secret random number 
and calculated
Bob publishes the point. Alice chooses the random number 
and
Alice sends (7966,6354) and (5011,2629) to Bob, who multiplies the first of these point by

Bob then subtracts the result from the last point that Alice sends him. Note that he subtracts by adding the point with the second coordinate negated:
Bob has therefore received Alice’s message.
Acknowledgements
This research work is supported by University Grant commission (UGC) New Delhi, India under the Junior Research Fellowship student scheme..
Cite this paper
ManojKumar,PratikGupta, (2016) Cryptographic Schemes Based on Elliptic Curves over the Ring Zp[i]. Applied Mathematics,07,304-312. doi: 10.4236/am.2016.73027
References
- 1. Koblitz, A.H., Koblitz, N. and Menezes, A. (2011) Elliptic Curve Cryptography: The Serpentine Course of a Paradigm Shift. Journal of Number Theory, 131, 781-814.
http://dx.doi.org/10.1016/j.jnt.2009.01.006 - 2. Miller, V. (1985) Use of Elliptic Curves in Cryptography. Advances in Cryptology-CRYPTO, 85, 417-426.
- 3. Chillali, A. (2011) Elliptic Curve over Ring. International Mathematical Forum, 6, 1501-1505.
- 4. Koblitz, N. (1987) Elliptic Curve Cryptosystem. Journal of Mathematics Computation, 48, 203-209.
http://dx.doi.org/10.1090/S0025-5718-1987-0866109-5 - 5. Kumar, S., Suneetha, C. and Chandrasekh, A. (2012) Encryption of Data Using Elliptic Curve over Finite Fields. International Journal of Distributed and Parallel Systems (IJDPS), 3, No. 1.
- 6. Schoof, R. (1985) Elliptic Curves over Finite Fields and the Computation of Square Roots Mod p. Mathematics of Computation, 44, 483-494.
- 7. Srivastava, K. and Nand, G. (2015) Elliptic Curves for Data Provenance. Procedia Computer Science, 45, 470-476.
http://dx.doi.org/10.1016/j.procs.2015.03.082 - 8. Hankerson, D., Menezes, J.A. and Vanstone, S. (2004) Guide to Elliptic Curve Cryptography. Springer-Verlag, Germany.
- 9. Silverman, J. (1986) The Arithmetic of Elliptic Curves. Springer, New York.
http://dx.doi.org/10.1007/978-1-4757-1920-8 - 10. Stinson, D.R. (2006) Cryptography Theory and Practice. Chapman and Hall/CRC, United Kingdom.
- 11. Washington, L.C. (2008) Elliptic Curves Number Theory and Cryptography. Chapman and Hall/CRC, United Kingdom.
http://dx.doi.org/10.1201/9781420071474 - 12. Gilbert, W.J. (2004) Modern Algebra with Application. Willey-Interscience, New York.
- 13. Hardy, G.H. and Wright, E.M. (1938) An Introduction to the Theory of Numbers. Oxford University Press, United Kingdom.
- 14. Gallian, J.A. (1998) Contemporary Abstract Algebra. Narosa Publishing House, New Delhi.
























































