Applied Mathematics
Vol.5 No.4(2014), Article ID:43578,6 pages DOI:10.4236/am.2014.54066
Project Scheduling Problem with Uncertain Variables
Liang Lin*, Ting Lou, Ni Zhan
College of Science, Guilin University of Technology, Guilin, China
Email: *543990117@qq.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 3 January 2014; revised 3 February 2014; accepted 10 February 2014
ABSTRACT
Project scheduling problem is mainly to determine the schedule of allocating resources in order to balance the total cost and the completion time. This paper chiefly uses chance theory to introduce project scheduling problem with uncertain variables. First, two types of single-objective programming models with uncertain variables as uncertain chance-constrained model and uncertain maximization chance-constrained model are established to meet different management requirements, then they are extended to multi-objective programming model with uncertain variables.
Keywords:Project Scheduling Problem; Uncertain Variable; Single-Objective Programming; Multi-Objective Programming

1. Introduction
Project scheduling problem is mainly to determine the schedule of allocating resources in order to balance the total cost and the completion time. A typical project scheduling problem can be described as follows: there are many activities in a project. There are tight-front relations among some projects because of the technical request. Activity can’t be processed before its all tight-front works are finished. The structure of entire project can be described by a directed acyclic network graph. The pitch point represents transformation from an activity to another activity in the graph, and the arc represents tight-front relations among activities. A feasible plan can be defined as follows: the schedule of each activity has been determined; also each activity satisfies tight-front relation and resource restraint.
Researchers have studied project scheduling problem in certain or uncertain environments since 1960s. Kelley [1] [2] initially presented function relationship between project cost and activity duration times, and established a mathematical model of deterministic project scheduling problem with objective of minimizing the total cost. In 1960, Freeman [3] [4] introduced probability theory into project scheduling problem. Charnes et al. [5] studied stochastic project scheduling problem via chance-constrained programming. Golenko-Ginzburg and Gonik [6] set up an expected cost minimization model of project scheduling problem under some deterministic resource constraint. Finally, Ke and Liu [7] built three stochastic models as expected cost model, α-cost model and probability maximization model via hybrid intelligent algorithm to relatively comprehensively solve stochastic project scheduling problem. But the uncertainty is assumed as randomness in the above work.
Nevertheless, in real world, much uncertainty may not be replaced by randomness. For instance, fuzzy set theory, which was introduced by Zadeh [8] , describes another uncertainty. Prade [9] first applied fuzzy set theory into the project scheduling problem in 1979. In 2004, Ke and Liu [10] built three fuzzy models via hybrid intelligent algorithm, and they quickly applied fuzzy set theory into the project scheduling problem successfully. Furthermore, in 2007, Ke and Liu [11] presented random fuzzy models, for example, the duration time of each activity is stochastic and stochastic parameters are fuzzy variables.
This paper chiefly introduces project scheduling problem with uncertain variables via chance theory. First, two types of single-objective programming models with uncertain variables as uncertain chance-constrained model and uncertain maximization chance-constrained model are established to meet different management requirements, and then they are extended to multi-objective programming model with uncertain variables.
2. Theoretical Preparation
2.1. Uncertain Variable
In many cases, randomness and fuzziness simultaneously appear in uncertain phenomena. In 1978, the concept of fuzzy random variable was introduced by Kwakernaak [12] [13] in order to describe these phenomena. Afterwards the concept of fuzzy random variable was developed by several researchers such as Puri and Ralescu [14] , Kruse and Meyer [15] , and Liu and Liu [16] according to different requirements of measure. Furthermore, Liu [17] first proposed the concept of random fuzzy variable. More generally, Liu [18] puts forward the concept of uncertain variables. As follows:
Definition 1 (Liu [18] ) an uncertain variable is a measurable function 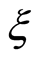 from an uncertainty space
from an uncertainty space 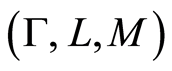 to the set of real numbers, i.e., for any Borel set B of real numbers, the set
to the set of real numbers, i.e., for any Borel set B of real numbers, the set
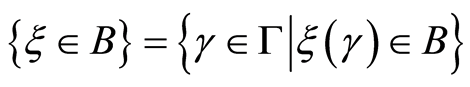 (1)
(1)
is an event.
It is very clear that uncertain variable is very different from random variable (Kolmogorov [19] ) and fuzzy variable (Zadeh [8] ). Roughly speaking, a random variable is a function from a probability space to the set of real numbers, and a fuzzy set is a function from a possibility space to the set of real numbers.
2.2. Chance Measure
In many cases, uncertainty and randomness simultaneously appear in a complex system. In order to describe this phenomenon, the concept of chance measure was proposed by Liu [20] in 2013:
Definition 2 (Liu [20] ) Let 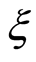 be an uncertain random variable, and let
be an uncertain random variable, and let 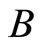 be a Borel set of real numbers. Then the chance measure of uncertain random event
be a Borel set of real numbers. Then the chance measure of uncertain random event 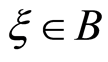 is defined by
is defined by
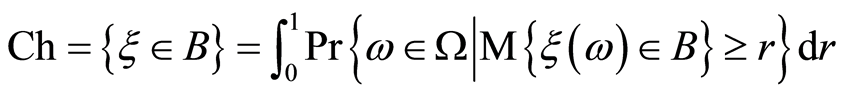 (2)
(2)
Definition 3 (Liu [11] ) Let 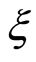 be a random fuzzy variable on the possibility space
be a random fuzzy variable on the possibility space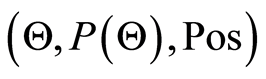 , and let
, and let 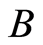 be a Borel set of real numbers. Then the chance of random fuzzy event
be a Borel set of real numbers. Then the chance of random fuzzy event 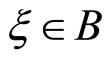 is a function from (0, 1] to [0, 1], defined as
is a function from (0, 1] to [0, 1], defined as
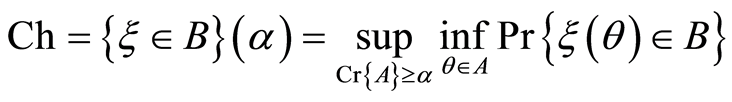 (3)
(3)
3. Problem Assumptions
In a real world application, a large engineering project is a big complex system. In order to establish the corresponding mathematical models, we must give some simplifications and assumptions to meet different management requirements.
Assumption 1): All of the costs are obtained by loans with some given interest rate;
Assumption 2): Each activity can start only if the loan needed is allocated and all the foregoing activities are finished;
Assumption 3): Duration time of each activity is assumed to a continuous and an uncertain variable;
Assumption 4): Each man-power needed for each activity is an uncertain variable; a part of duration time of each activity is inversely proportional to the number of workers;
Assumption 5): The cost needed for each activity is only considered to workers’ wages and loans with some given interest rate.
4. Models Establishment
Generally speaking, a project scheduling problem can be described by a directed acyclic graph like Figure 1.
Let 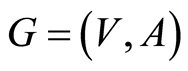 represents a project, where
represents a project, where 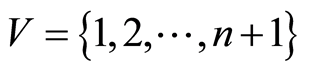 is the set of nodes standing for the milestones and
is the set of nodes standing for the milestones and  is the set of arcs representing the activities of the project.
is the set of arcs representing the activities of the project.
Let us first introduce the following mathematical signs and symbols:
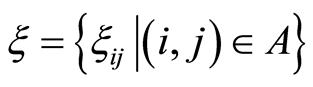 , where
, where 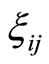 are uncertain variables and
are uncertain variables and 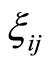 are duration times of activities represented by
are duration times of activities represented by 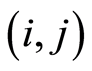 in
in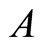 ;
;
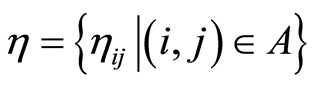 , where
, where  are uncertain variables and
are uncertain variables and 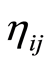 are numbers of workers for activities represented by
are numbers of workers for activities represented by 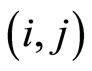 in
in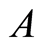 ;
;
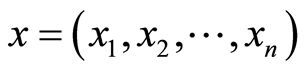 , where
, where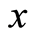 is a decision vector and
is a decision vector and  represents the allocating time of all the loans needed for activities represented by
represents the allocating time of all the loans needed for activities represented by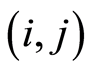 in
in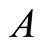 ;
;
 , where
, where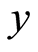 is a decision vector and
is a decision vector and 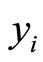 represents the allocating number of workers needed for activities represented by
represents the allocating number of workers needed for activities represented by 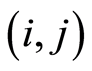 in
in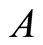 ;
;
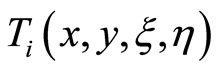 : the starting times of activity
: the starting times of activity 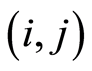 in
in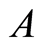 ;
;
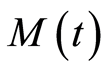 : the number of workers needed for the project at the time point denoted as
: the number of workers needed for the project at the time point denoted as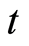 ;
;
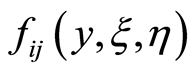 : the duration time of activity
: the duration time of activity 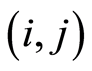 in
in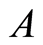 ;
;
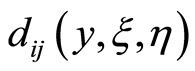 : the cost needed for activity
: the cost needed for activity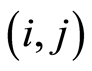 in
in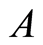 ;
;
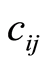 : the fixed cost needed for activity
: the fixed cost needed for activity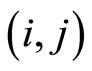 in
in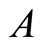 ;
;
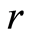 : the interest rate;
: the interest rate;
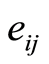 : the coefficient of wages needed for activity
: the coefficient of wages needed for activity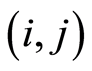 in
in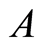 (Yuan per person in unit time);
(Yuan per person in unit time);
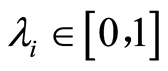 : the coefficients about the irrelevant part between the duration time and the number of workers of activity
: the coefficients about the irrelevant part between the duration time and the number of workers of activity 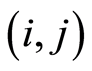 in
in ;
;
According to the assumption (4), the duration time of activity  in
in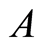 can be calculated by
can be calculated by
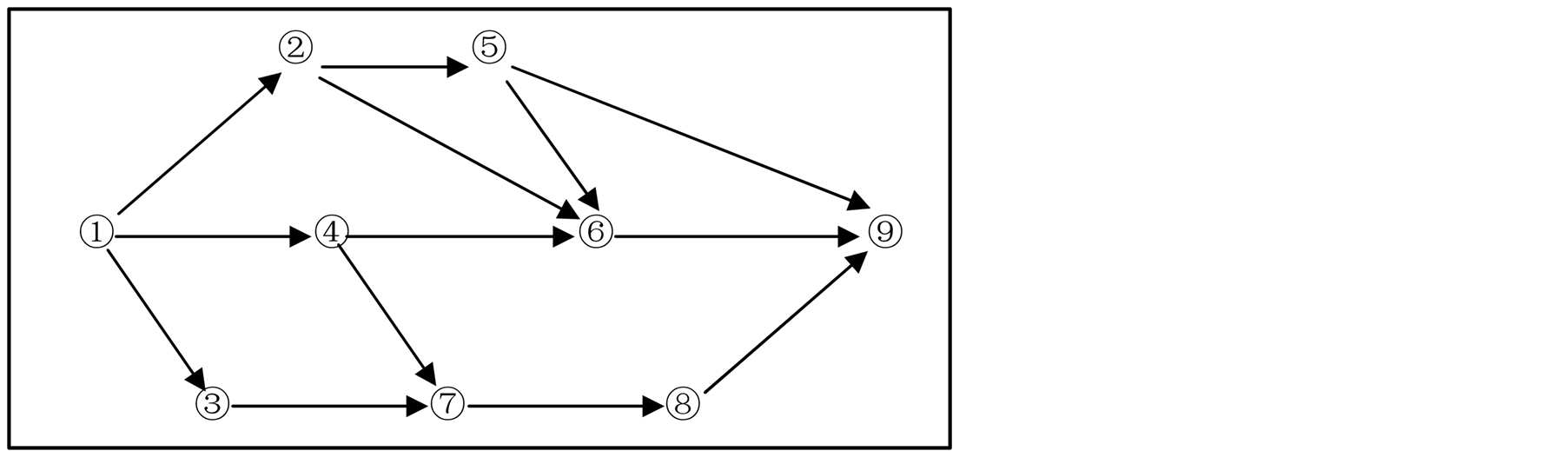
Figure 1. Engineering drawing.
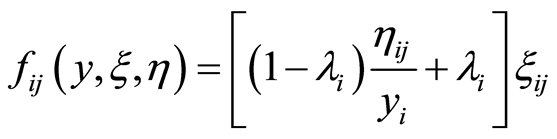 (4)
(4)
Obviously,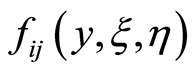 is an uncertain variable.
is an uncertain variable.
According to the assumption (5), the costs needed for activity 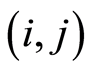 in
in 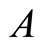 can be calculated by
can be calculated by
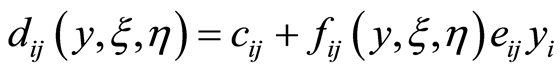 (5)
(5)
According to the assumption (2), 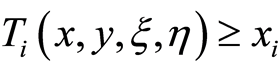 and
and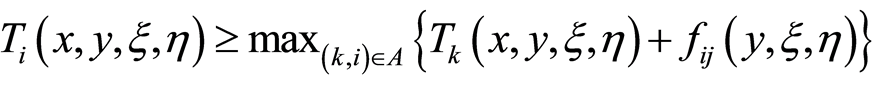 , we can get
, we can get
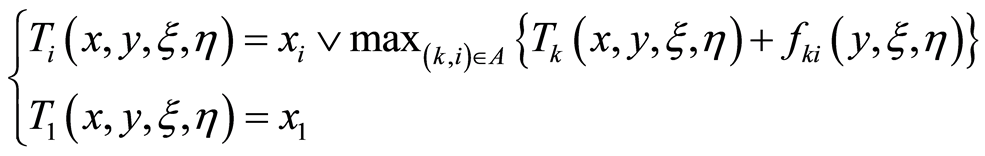 (6)
(6)
Then the completion time of the total project can be calculated by
 (7)
(7)
The total cost of the project can be calculated by
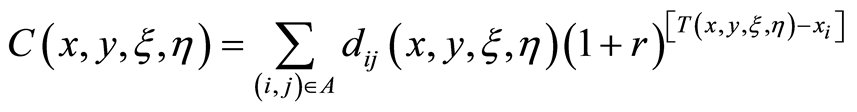 (8)
(8)
Obviously, we can get
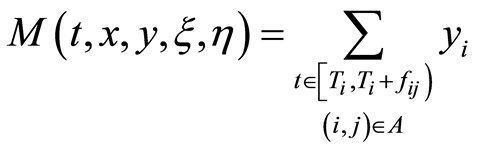 (9)
(9)
The maximal numbers of workers needed for the project can be denoted as
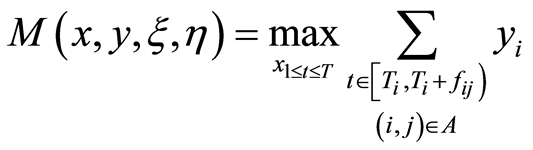 (10)
(10)
where 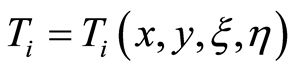 and
and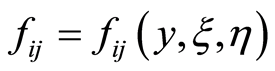 .
.
As these basic formulas have been given in the above section, we can establish different hybrid programming models to meet different management requirements.
4.1. Single-Objective Programming Models with Uncertain Variables
Model 1: uncertain chance-constrained model:
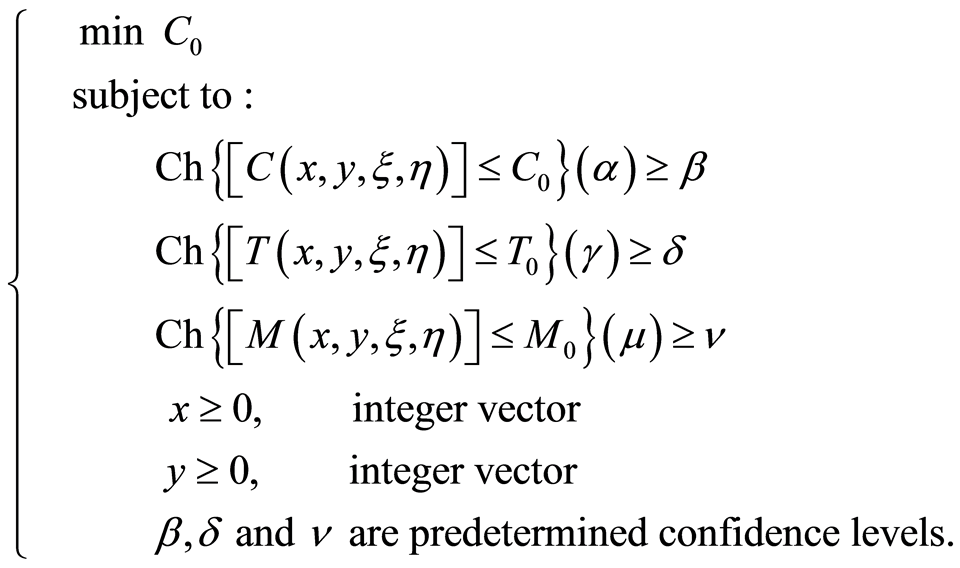
where 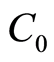 is the total cost of the project,
is the total cost of the project, 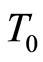 is the total times of the project and
is the total times of the project and 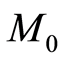 is the total numbers of workers of the total project.
is the total numbers of workers of the total project.
Model 2: uncertain maximization chance-constrained model
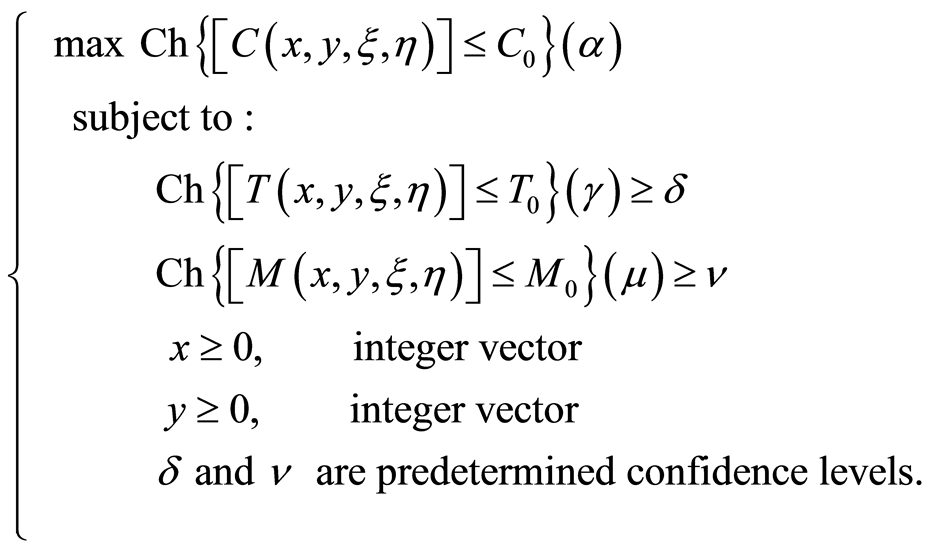
where 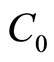 is the total cost of the project,
is the total cost of the project, 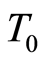 is the total times of the project and
is the total times of the project and  is the total numbers of workers of the total project.
is the total numbers of workers of the total project.
4.2. Multi-Objective Programming Models with Uncertain Variables
If we consider both minimal cost and minimal numbers of workers of the total project, we can build the corresponding multi-objective programming models with uncertain variable.
Model 1: uncertain chance-constrained model
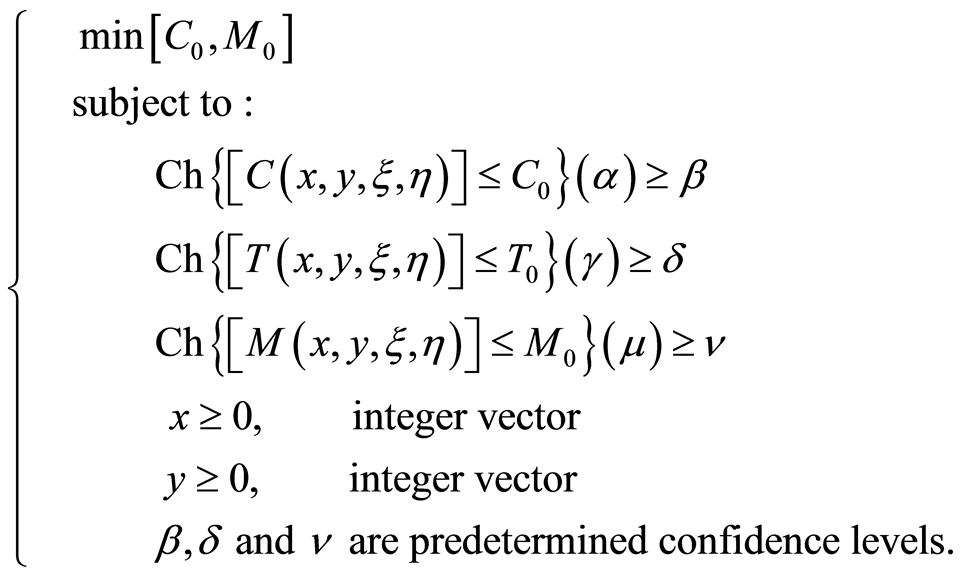
where is the total cost of the project,
is the total cost of the project, 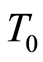 is the total times of the project and
is the total times of the project and 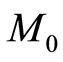 is the total numbers of workers of the total project.
is the total numbers of workers of the total project.
Model 2: uncertain maximization chance-constrained model
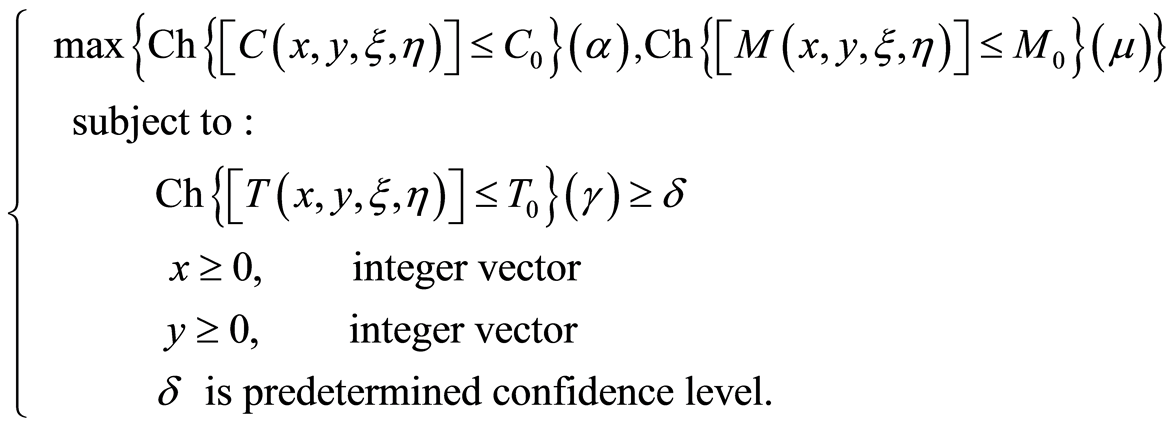
where 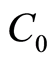 is the total cost of the project,
is the total cost of the project, 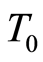 is the total times of the project and
is the total times of the project and 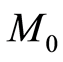 is the total numbers of workers of the total project.
is the total numbers of workers of the total project.
5. Conclusion
Considering the process of practical application, a large engineering project is a large complex system. This article embarks from the actual. On the basis of the time constraints, allocating the number of workers is also an important factor which cannot be ignored. That is also the innovation of this paper. We set up corresponding mathematical models, so as to adapt to different management needs. In the further study, we can put the above models to the practical problems to meet the needs of reality.
Funding
This research was supported by the National Natural Science Foundation of China (71361002).
References
- Kelley Jr., J.E. (1961) Critical Path Planning and Scheduling: Mathematical Basis. Operations Research, 9, 296-320. http://dx.doi.org/10.1287/opre.9.3.296
- Kelley Jr., J.E. (1963) The Critical Path Method: Resources Planning and Scheduling. Industrial Scheduling, 13, 347- 365.
- Freeman, R.J. (1960) A Generalized PERT. Operations Research, 8, 281. http://dx.doi.org/10.1287/opre.8.2.281
- Freeman, R.J. (1960) A Generalized Network Approach to Project Activity Sequencing. IRE Transactions on Engineering Management, 7, 103-107. http://dx.doi.org/10.1109/IRET-EM.1960.5007550
- Charnes, A. and Cooper, W.W. (1956) Chance-Constrained Programming. Management Science, 6, 73-79. http://dx.doi.org/10.1287/mnsc.6.1.73
- Golenko-Ginzburg, D. and Gonik, A. (1997) Stochastic Network Project Scheduling with Non-Consumable Limited Resources. International Journal of Production Economics, 48, 29-37.
- Ke, H. and Liu, B.D. (2005) Project Scheduling Problem with Stochastic Activity Duration Times. Applied Mathematics and Computation, 168, 342-353. http://dx.doi.org/10.1016/j.amc.2004.09.002
- Zadeh, L.A. (1965) Fuzzy Sets. Information and Control, 8, 338-353. http://dx.doi.org/10.1016/S0019-9958(65)90241-X
- Prade, H. (1979) Using Fuzzy Set Theory in a Scheduling Problem: A Case Study. Fuzzy Sets and Systems, 2, 153-165. http://dx.doi.org/10.1016/0165-0114(79)90022-8
- Ke, H. and B.D. Liu (2004) Project Scheduling Problem with Fuzzy Activity Duration Times. Proceedings of IEEE International Conference on Fuzzy Systems, 2, 819-823.
- Ke, H. and Liu, B.D. (2007) Project Scheduling Problem with Mixed Uncertainty of Randomness and Fuzziness. European Journal of Operational Research, 183, 135-147. http://dx.doi.org/10.1016/j.ejor.2006.09.055
- Kwakernaak, H. (1978) Fuzzy Random Variables—I: Definitions and Theorems. Information Sciences, 15, 1-29. http://dx.doi.org/10.1016/0020-0255(78)90019-1
- Kwakernaak, H. (1979) Fuzzy Random Variables—II: Algorithms and Examples for the Discrete Case. Information Sciences, 17, 253-278. http://dx.doi.org/10.1016/0020-0255(79)90020-3
- Puri, M.L. and Ralescu, D.A. (1986) Fuzzy Random Variables. Journal of Mathematical Analysis and Applications, 114, 409-422. http://dx.doi.org/10.1016/0022-247X(86)90093-4
- Kruse, R. and Meyer, K.D. (1987) Statistics with Vague Data. Springer, Berlin. http://dx.doi.org/10.1007/978-94-009-3943-1
- Liu, Y.K. and Liu, B. (2003) Fuzzy Random Variables: A Scalar Expected Value Operator. Fuzzy Optimization and Decision Making, 2, 143-160. http://dx.doi.org/10.1023/A:1023447217758
- Liu, B.D. (2002) Random Fuzzy Dependent-Chance Programming and Its Hybrid Intelligent Algorithm. Information Sciences, 141, 259-271. http://dx.doi.org/10.1016/S0020-0255(02)00176-7
- Liu, B.D. (2007) Uncertainty Theory. 2nd Edition, Springer-Verlag, Berlin.
- Kolmogorov, A.N. (1933) Grundbegriffe der Wahrscheinlichkeitsrechnung. Julius Springer, Berlin. http://dx.doi.org/10.1007/978-3-642-49888-6
NOTES

*Corresponding author.

