Smart Grid and Renewable Energy
Vol.2 No.3(2011), Article ID:6597,11 pages DOI:10.4236/sgre.2011.23032
Optimal Scheduling of Cascaded Hydrothermal Systems Using a New Improved Particle Swarm Optimization Technique
![]()
Department of Power Engineering, Jadavpur University, Kolkata, India.
Email: kkm567@yahoo.co.in
Received February 18, 2011; revised May 12, 2011; accepted May 19, 2011.
Keywords: Hydrothermal Systems, Cascaded Reservoirs, Self-Organizing Hierarchical Particle Swarm Optimization with Time-Varying Acceleration Coefficients (SOHPSO_TVAC)
ABSTRACT
Optimum scheduling of hydrothermal plants generation is of great importance to electric utilities. Many evolutionary techniques such as particle swarm optimization, differential evolution have been applied to solve these problems and found to perform in a better way in comparison with conventional optimization methods. But often these methods converge to a sub-optimal solution prematurely. This paper presents a new improved particle swarm optimization technique called self-organizing hierarchical particle swarm optimization technique with time-varying acceleration coefficients (SOHPSO_TVAC) for solving short-term economic generation scheduling of hydrothermal systems to avoid premature convergence. A multi-reservoir cascaded hydrothermal system with nonlinear relationship between water discharge rate, power generation and net head is considered here. The performance of the proposed method is demonstrated on two test systems comprising of hydro and thermal units. The results obtained by the proposed methods are compared with other methods. The results show that the proposed technique is capable of producing better results.
1. Introduction
The optimum scheduling of hydrothermal plants is one of the important planning task in power system operation. The generation scheduling problem consists of determining the optimal operation strategy for the next scheduling period, subjected to a variety of constraints. The main objective is to allocate generations of hydroelectric and thermal plants in such a way so as to minimize the total operation cost of the systems subjected to variety of constraints. With the insignificant operating cost of hydroelectric plants, the problem of minimizing the operational cost of a hydrothermal system essentially reduces to that of minimizing the fuel cost for thermal plants under the various constraints on the hydraulic and power system network. It is basically a nonlinear programming problem involving non-linear objective function and a mixture of linear and non-linear constraints.
The main constraints include the cascaded nature of the hydraulic network, the time coupling effect of the hydro sub problem where the water inflow of an earlier time interval affects the discharge capability at a later period of time, the varying hourly reservoir inflows, the physical limitations on the reservoir storage and turbine flow rate, the varying system load demand and the loading limits of both thermal and hydro plants.
The hydrothermal scheduling problem has been the subject of investigation for several decades and many methods have been applied to solve this problem. Some of these solution methods include decomposition techniques [1], dynamic programming [2], semi-definite programming [3] and concept of non-linear network flow [4]. In recent times, optimal hydrothermal scheduling problems have been solved by different heuristic techniques such as genetic algorithm [5] simulated annealing technique [6], evolutionary programming technique [7] etc. Yu, et al. used particle swarm optimization technique to solve short-term hydrothermal scheduling problem [8] with an equivalent thermal unit having smooth cost functions. A modified hybrid differentia evolution technique was applied by Lakshminarasimman, et al. [9] to solve short-term hydrothermal generation scheduling problems with promising results. A comparison of particle swarm optimization and dynamic programming for large scale hydro unit load dispatch was made by Cheng, et al. [10]. Recently, Catalao, et al [11] applied mixedinteger quadratic programming method to determine scheduling of head dependent cascaded hydro systems.
Particle swarm optimization (PSO) happens to be a comparatively new combinatorial metaheuristic technique which is based on the social metaphor of bird flocking or fish schooling [12]. This algorithm has come to existence in mid 90’s and has gained prominence from late 90’s. The PSO technique has been applied to various fields of power system optimization. Gaing used PSO to solve economic dispatch problem considering generator constraints [13]. Abido proposed a revised PSO technique for optimal design of voltage stabilizer [14]. Park, et al. presented a method for solving economic dispatch with non-smooth cost functions [15]. A hybrid method for optimal scheduling of short-term electric power generation of cascaded hydroelectric plants based on particle swarm optimization and chance-constrained programming was presented by Jiekang, et al. [16].
A novel parameter automation strategy called self-organizing hierarchical particle swarm optimization technique with time-varying acceleration coefficients (SOHPSO_TVAC) is applied in this paper for the hydrothermal scheduling to address the problem of premature convergence. In this case, the particle velocities are reinitialized whenever the population stagnates at local optima during the search. A relatively high value of the cognitive component results in excessive wandering of particles while a higher value of the social component causes premature convergence of particles. Hence, time-varying acceleration coefficients (TVAC) [17] are employed to strike a proper balance between the cognitive and social component during the search. The proposed approach was first tested on a simple test system comprising of one equivalent thermal unit and four cascaded hydro unit and then the effectiveness of the SOHPSO_TVAC was demonstrated on a more practical system comprising of six thermal units and four cascaded hydro units. The results have been compared with other evolutionary methods and found to be superior.
2. Problem Formulation
Economic generation scheduling of hydrothermal systems involves the optimization of a problem with nonlinear objective function subject to a mixture of linear, non-linear constraints. As the fuel cost of hydroelectric plants is insignificant in comparison with that of thermal power plants, the objective is to minimize the fuel cost of thermal power plants, while making use of the availability of hydro-resources as much as possible. The objective function and associated constraints are described as follows:
Minimize
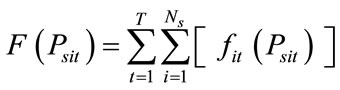 (1)
(1)
where, 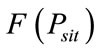 is the total fuel cost,
is the total fuel cost, ![]() is the number of time interval for scheduling horizon,
is the number of time interval for scheduling horizon, 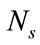 is the number of thermal plants and
is the number of thermal plants and 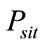 is the power generation by the i-th thermal plants at time t.
is the power generation by the i-th thermal plants at time t.
Conventionally, the fuel cost curve for any unit can be represented by segments of quadratic functions of the active power output of the generator and can be expressed as
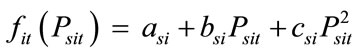 (2)
(2)
where,  ,
,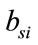 ,
, : fuel cost coefficients of the i-th thermal unit.
: fuel cost coefficients of the i-th thermal unit.
For more practical and accurate modeling of fuel cost function, the above expression needs to be modified suitably. Modern thermal power plants comprise of generating units having multi-valve steam turbines in order to incorporate flexible operational facilities. The generating units with multi-valve turbines have very different cost curve compared with that defined by (2). The effect of valve-point effect loading may be considered by adding a sinusoidal function [9] to the quadratic cost function described above. Hence, the function described by (2) is revised as follows:
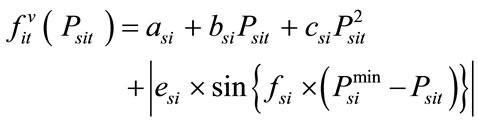 (3)
(3)
where 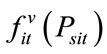 is the fuel cost function of thermal units including the valve point loading effect and
is the fuel cost function of thermal units including the valve point loading effect and  are fuel cost coefficients of the i-th thermal generating unit reflecting the valve-point effect.
are fuel cost coefficients of the i-th thermal generating unit reflecting the valve-point effect.
The above objective function described by (3) is to be minimized subject to a variety of constraints as follows:
1) Demand constraints The total power generated must balance the power demand plus losses, at each time interval over the entire scheduling period
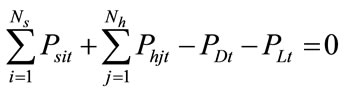 (4)
(4)
where 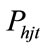 is the power generation of jth hydro generating unit at time t,
is the power generation of jth hydro generating unit at time t,  is power demand at time t and
is power demand at time t and  is total transmission loss at the corresponding time.
is total transmission loss at the corresponding time.
The hydropower generation is a function of water discharge rate and reservoir storage volume, which can be described by (5) as follow:
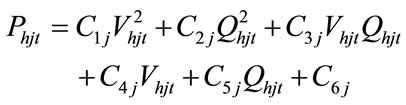 (5)
(5)
where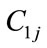 ,
,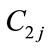 ,
,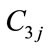 ,
,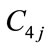 ,
,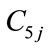 ,
,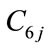 are power generation coefficients of j th hydro generating unit,
are power generation coefficients of j th hydro generating unit, 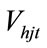 is the storage volume of j-th reservoir at time t and
is the storage volume of j-th reservoir at time t and 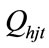 is water discharge rate of j-th reservoir at time t.
is water discharge rate of j-th reservoir at time t.
2) Power generation constraints
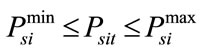 (6)
(6)
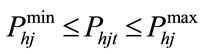 (7)
(7)
where 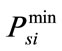 and
and 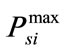 are the minimum and maximum power generation by i-th thermal generating unit,
are the minimum and maximum power generation by i-th thermal generating unit,  and
and 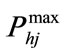 are the minimum and maximum power generation by the j-th hydro generating unit respectively.
are the minimum and maximum power generation by the j-th hydro generating unit respectively.
3) Water dynamic balance
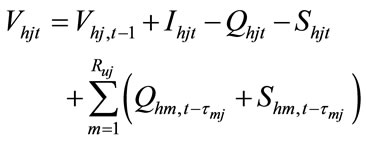 (8)
(8)
where 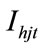 is natural inflow of j-th hydro reservoir at time t,
is natural inflow of j-th hydro reservoir at time t, 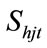 is spillage discharge rate of j-th hydro generating unit at time t,
is spillage discharge rate of j-th hydro generating unit at time t, 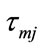 is the water transport delay from reservoir m to j and
is the water transport delay from reservoir m to j and  is the number of upstream hydro generating plants immediately above the j-th reservoir.
is the number of upstream hydro generating plants immediately above the j-th reservoir.
4) Reservoir storage volume constraints
 (9)
(9)
where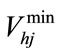 ,
,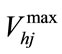 are the minimum and maximum storage volume of j th reservoir.
are the minimum and maximum storage volume of j th reservoir.
5) Water discharge rate limit
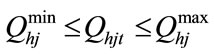 (10)
(10)
where,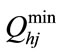 and
and 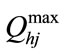 are the minimum and maximum water discharge rate of the j-th reservoir respectively.
are the minimum and maximum water discharge rate of the j-th reservoir respectively.
3. Overview of Some PSO Strategies
There are several variants of PSO. Some of the commonly used PSo are discussed in the following sections.
3.1. Classical PSO
The Particle Swarm Optimization (PSO) is one of the recent developments in the category of heuristic optimization technique. Kennedy and Eberhart [12] originally developed the PSO concept based on the behavior of individuals (i.e. particles or agents) of a swarm or group. PSO, as an optimization tool, provides a populationbased search procedure in which individuals called agents or particles change their position with time. In a PSO algorithm, the particles fly around the multidimensional search space in order to find the optimum solution. Each particle adjusts its position according to its own experience and the experience of neighboring particle.
Let in a physical d-dimensional search space, the position and velocity of the i-th particle (i.e. i-th individual in the population of particles) be represented as the vectors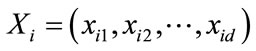 and
and 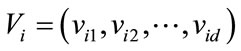 respectively. The previous best position of the i-th particle is recorded and represented as
respectively. The previous best position of the i-th particle is recorded and represented as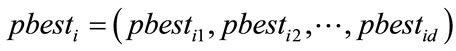 . The index of the best particle among all the particles in the group is represented by the
. The index of the best particle among all the particles in the group is represented by the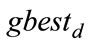 . The modified velocity and position of each particle can be calculated using the current velocity and the distance from
. The modified velocity and position of each particle can be calculated using the current velocity and the distance from 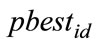 to
to 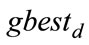 as shown below:
as shown below:
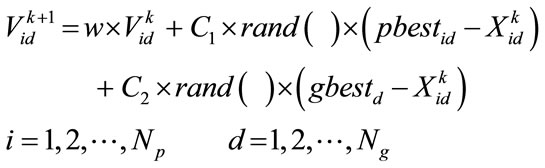 (11)
(11)
where 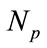 is the number of particles in a swarm or group,
is the number of particles in a swarm or group, 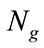 is the number of members or elements in a particle,
is the number of members or elements in a particle, 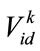 is the velocity of individual i at iteration k,
is the velocity of individual i at iteration k, ![]() is the weight parameter or swarm inertia,
is the weight parameter or swarm inertia, 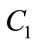 and
and  are the acceleration constants and
are the acceleration constants and 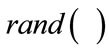 is uniform random number in the range [0 1].
is uniform random number in the range [0 1].
The updated velocity can be used to change the position of each particle in the swarm as depicted in (12) as:
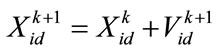 (12)
(12)
Suitable selection of inertia weight ![]() provides a balance between global and local explorations, thus requiring less iteration on average to find a sufficiently optimal solution. In general, the inertia weight
provides a balance between global and local explorations, thus requiring less iteration on average to find a sufficiently optimal solution. In general, the inertia weight ![]() is set according to the following equation:
is set according to the following equation:
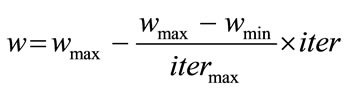 (13)
(13)
where 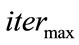 is the maximum number of iterations and
is the maximum number of iterations and 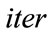 is the current number of iterations.
is the current number of iterations.
The constants  and
and 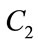 represent the weighting of the stochastic acceleration terms that pull each particle toward the
represent the weighting of the stochastic acceleration terms that pull each particle toward the 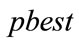 and
and 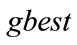 positions.
positions.
3.2. Concept of Time-Varying Acceleration Coefficients (TVAC)
It is observed from (11) that the search toward the optimum solution is heavily dependent on the two stochastic acceleration components (i.e. the cognitive component and the social component). Thus, it is very important to control these two components properly in order to get optimum solution efficiently and accurately. It has been reported [18] that in PSO, problem-based tuning of parameters is a key factor to find the optimum solution accurately and efficiently. Kennedy and Eberhart [12] reported that a relatively higher value of the cognitive component, compared with the social component, results in excessive roaming of individuals through a larger search space. On the other hand, a relatively high value of the social component may lead particles to rush toward a local optimum prematurely.
In general, for any population-based optimization method like PSO, it is always desired to encourage the individuals to wander through the entire search space, during the initial part of the search, without clustering around local optima. In contrast, during the latter stages, it is desirable to enhance convergence towards the global optima so that optimum solution can be achieved efficiently. For this, the concept of parameter automation strategy called Time Varying acceleration Coefficients (TVAC) had been introduced [17]. The main purpose of this concept is to enhance the global search capability during the early part of the optimization process and to promote the particles to converge toward the global optimum at the end of the search. For this, the cognitive component should be reduced while the social component should be increased during search procedure. In TVAC, this can be achieved by changing the acceleration coefficients with time. With a large cognitive component and small social component at the beginning, the particles are encouraged to move around the search space, instead of moving towards the population best prematurely. On the other hand, during the latter stage of optimization, a small cognitive component and a large social component encourage the particles to converge towards the global optimum. The concept of time varying acceleration coefficients (TVAC) can be introduced mathematically as follows [17].
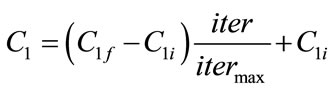 (14)
(14)
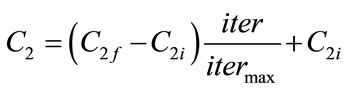 (15)
(15)
where  are constants representing initial and final values of cognitive and social acceleration factors respectively.
are constants representing initial and final values of cognitive and social acceleration factors respectively.
3.3. Self-Organizing Hierarchical PSO with TVAC (SOHPSO_TVAC)
It is seen that the classical PSO is either based on a constant inertia weight factor or a linearly varying inertia weight factor. It is reported that the particles in classical PSO may converge to a local minimum prematurely due to lack of diversity in the population, particularly for complex problems [17]. In SOHPSO_TVAC, the previous velocity term in (11) is kept at zero. It is observed that in the absence of previous velocity term the particles rapidly rush towards a local optimum solution and then stagnate due to the lack of momentum. In fact in the absence of velocity term, the optimum solution depends highly on the initial population. To overcome this difficulty, the modulus of velocity vector of a particle is reinitialized with a random velocity (called reinitialization velocity) whenever it stagnates in the search space. Stagnation of particles highly influences the performance of PSO in searching global optimum. When a particle is stagnated, it’s 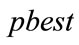 remains unchanged over a large number of iterations. When more particles are stagnated, the
remains unchanged over a large number of iterations. When more particles are stagnated, the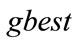 also remains unchanged and the PSO algorithm converges to a local minimum prematurely. The necessary momentum is imparted to the particles by reinitialization of velocity vector with a random velocity. The above method can be implemented as follows [17]:
also remains unchanged and the PSO algorithm converges to a local minimum prematurely. The necessary momentum is imparted to the particles by reinitialization of velocity vector with a random velocity. The above method can be implemented as follows [17]:
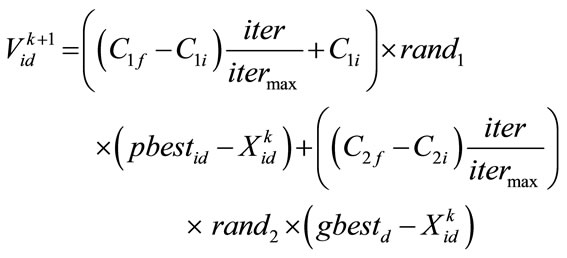 (16)
(16)
If 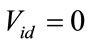 and
and 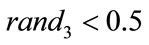 then
then
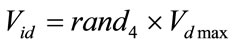 else
else 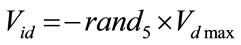 (17)
(17)
Thus a series of particle swarm optimizers are generated automatically inside the main PSO according to the behavior of the particles in the search space until the convergence criteria is satisfied. The variables 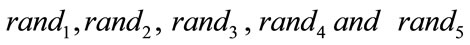 are numbers generated randomly between 0 and 1. A time varying reinitialization strategy is used to overcome the difficulties of selecting appropriate reinitialization velocities.
are numbers generated randomly between 0 and 1. A time varying reinitialization strategy is used to overcome the difficulties of selecting appropriate reinitialization velocities.
4. Development of the Proposed Algorithm
In this section, an algorithm based on SOHPSO_TVAC is described to obtain quality solutions for scheduling problems of hydrothermal systems with cascaded reservoirs. For any population based evolutionary algorithm like PSO, the representation of individuals and their elements is very important. For the present problem, the position of each particle (i.e. each individual in the population of particles) is composed of a set of elements and for the present problem it is the discharge rate of each hydro plant and the power generated by each thermal unit. The algorithm starts with the initialization process. Let 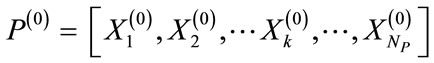 be the initial population of
be the initial population of 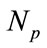 number of particles. For a system with
number of particles. For a system with 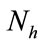 number of hydro units and
number of hydro units and 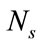 number of thermal units, position of k-th individual of a population is initialized randomly satisfying the constraints defined by (6) and (10) and can be represented by
number of thermal units, position of k-th individual of a population is initialized randomly satisfying the constraints defined by (6) and (10) and can be represented by
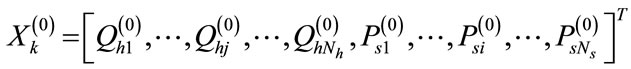 (18)
(18)
with  and
and . The elements
. The elements 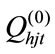 and
and 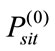 are the discharge rate of the j-th hydro plant and the power output of the i-th thermal unit at time t. The range of the elements
are the discharge rate of the j-th hydro plant and the power output of the i-th thermal unit at time t. The range of the elements  and
and  must satisfy the water discharge rate and the thermal generating capacity constraints as depicted in (6) and (10) respectively. Assuming the spillage in (8) to be zero for simplicity, the water discharge rate of the j-th hydro plant in the dependent interval is then calculated using (8) to meet exactly the restrictions on the initial and final reservoir storage. The dependent water discharge rate must satisfy the constraints in (10). At the same time, to meet exactly the power balance constraints, the thermal generation of the dependent thermal generating unit is calculated using (4). Thus, the initial generation is checked against all the constraints. If the constraints are satisfied then movement towards the next step is undertaken. Now, the algorithm can be described as follows:
must satisfy the water discharge rate and the thermal generating capacity constraints as depicted in (6) and (10) respectively. Assuming the spillage in (8) to be zero for simplicity, the water discharge rate of the j-th hydro plant in the dependent interval is then calculated using (8) to meet exactly the restrictions on the initial and final reservoir storage. The dependent water discharge rate must satisfy the constraints in (10). At the same time, to meet exactly the power balance constraints, the thermal generation of the dependent thermal generating unit is calculated using (4). Thus, the initial generation is checked against all the constraints. If the constraints are satisfied then movement towards the next step is undertaken. Now, the algorithm can be described as follows:
Step 1: Initialize randomly each particle according to the limit of each unit including individual dimensions, searching points and velocities according to (18). These initial particles must be feasible candidates for solutions that satisfy the practical operating constraints.
Step 2: For each particle, calculate fitness value according to (3).
Step3: If the fitness value is better than the best fitness value in history, set current value as the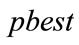 .
.
Step 4: Modify the member velocity of each particle according to (16) and reinitialize it according to (17).
Step 5: Choose the particle with the best fitness value of all the particles as the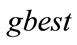 .
.
Step 6: If the number of iterations reaches the maximum, then go to Step 7 else go to Step 4.
Step 7: The individual that generates the latest 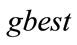 is the solution of the problem.
is the solution of the problem.
5. Simulation Results
The proposed algorithm was implemented using in house Matlab code on 3.0 MHz, 2.0 GB RAM PC. It was applied on two illustrative test systems to obtain the simulation results.
5.1. Test System-I
The proposed method has been initially applied to a test system consisting of four cascaded hydro units and an equivalent thermal plant.
This has been done to evaluate the performance of the proposed method in comparison to other population based methods [8,9], on the same test system. The scheduling period has been kept to 24 hours with one hour time interval. The water transport delay between connected reservoirs is also considered. For a direct comparison, effect of valve point loading is not considered in this case. The hydraulic network is shown in Figure 1. The load demand, hydro unit power generation coefficients, reservoir inflows, reservoir limits, the generation limits, cost coefficients of thermal unit and other data are taken from [8,9] and hence they are not shown in this paper.
The performance of PSO algorithm is quite sensitive to the various parameter settings. Tuning of parameters is essential in all PSO based methods. Based on empirical studies on a number of mathematical benchmark functions [17] it has been reported the best range of variation as 2.5 - 0.5 for 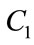 and 0.5 - 2.5 for
and 0.5 - 2.5 for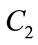 . The idea is to use a high initial value of the cognitive coefficient to make use of full range of the search space and to avoid premature convergence with a low social coefficient. We experimented with the same range and several combinations of the values of
. The idea is to use a high initial value of the cognitive coefficient to make use of full range of the search space and to avoid premature convergence with a low social coefficient. We experimented with the same range and several combinations of the values of 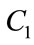 and
and 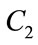 were tested. The best results were obtained for 2.5 - 1.2 for
were tested. The best results were obtained for 2.5 - 1.2 for 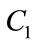 and 0.8 – 2.5 for
and 0.8 – 2.5 for 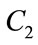 out of 50 trial runs. The optimization is done with a randomly initialized population of 30 swarms. The maximum iteration was set at 500.
out of 50 trial runs. The optimization is done with a randomly initialized population of 30 swarms. The maximum iteration was set at 500.

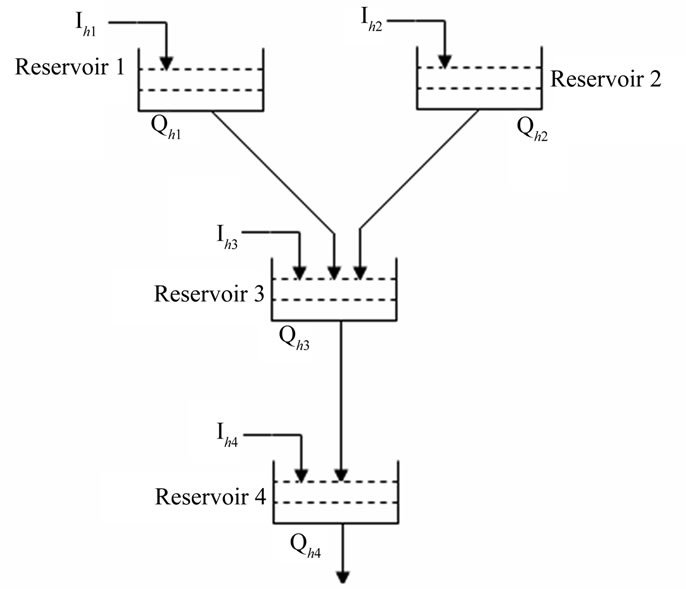
Figure 1. Hydraulic system networks.
Table 1 shows the optimal water discharge obtained by the proposed method. The optimal hydrothermal generation schedule along with demand for 24 hours is shown in Table 2. From the Table 2, it is clearly seen that total demand is met by the total power (both hydro and thermal power) generated in every scheduling interval. The proposed method converges to the optimal solution in 6.65 seconds. The optimal cost is found to be $ 922018.24. The results of the proposed method are compared with the results obtained by various versions of particle swarm optimization (PSO) techniques and genetic algorithm [8], modified hybrid differential evolution [9], improved PSO technique [19] and are shown in Table 3. It is clearly seen that the proposed method based SOHPSO_TVAC yields comparable results.
5.2. Test System-II
To evaluate the performance of the proposed method based on SOHPSO_TVAC, it was further applied to a test system that consists of a multi-chain cascade of four hydro units and six thermal units. The effect of valve point loading has been taken into account in this case to illustrate the robustness of the proposed algorithm. The scheduling period has been kept to 24 hours with one hour time interval. The water transport delay between connected reservoirs is also considered. The hydro sub-system configuration, hydro unit power generation coefficients, reservoir inflows, reservoir limits and other data related to hydro sub-system are same as that of test system-I [8,9]. The load demand, generation limits and cost coefficients of six thermal units are given in Tables 4 and 5 respectively.
In this case also, the parameters were selected separately. Out of 50 trial runs, best results were obtained for 2.5 - 1.0 for  and 1.08 - 2.5 for
and 1.08 - 2.5 for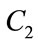 . The optimization is done with a randomly initialized population of 50 swarms. The maximum iteration for this case was set at 1000. The iteration number was increased at a step of fifty and beyond 1000 no improvement in results was obtained. Hence, maximum iteration was set at this value.
. The optimization is done with a randomly initialized population of 50 swarms. The maximum iteration for this case was set at 1000. The iteration number was increased at a step of fifty and beyond 1000 no improvement in results was obtained. Hence, maximum iteration was set at this value.
Optimal hourly water discharge rate obtained by the proposed algorithm for this system is shown in Table 6. Table 7" target="_self"> Table 7 presents the optimal hydro-generation schedule including total hydropower generation while Table 8 presents the optimal thermal-generation along with total thermal-power generation. From the Tables 7 and 8, it is clearly seen that total demand is exactly met by the total power (both hydro and thermal power) generated in
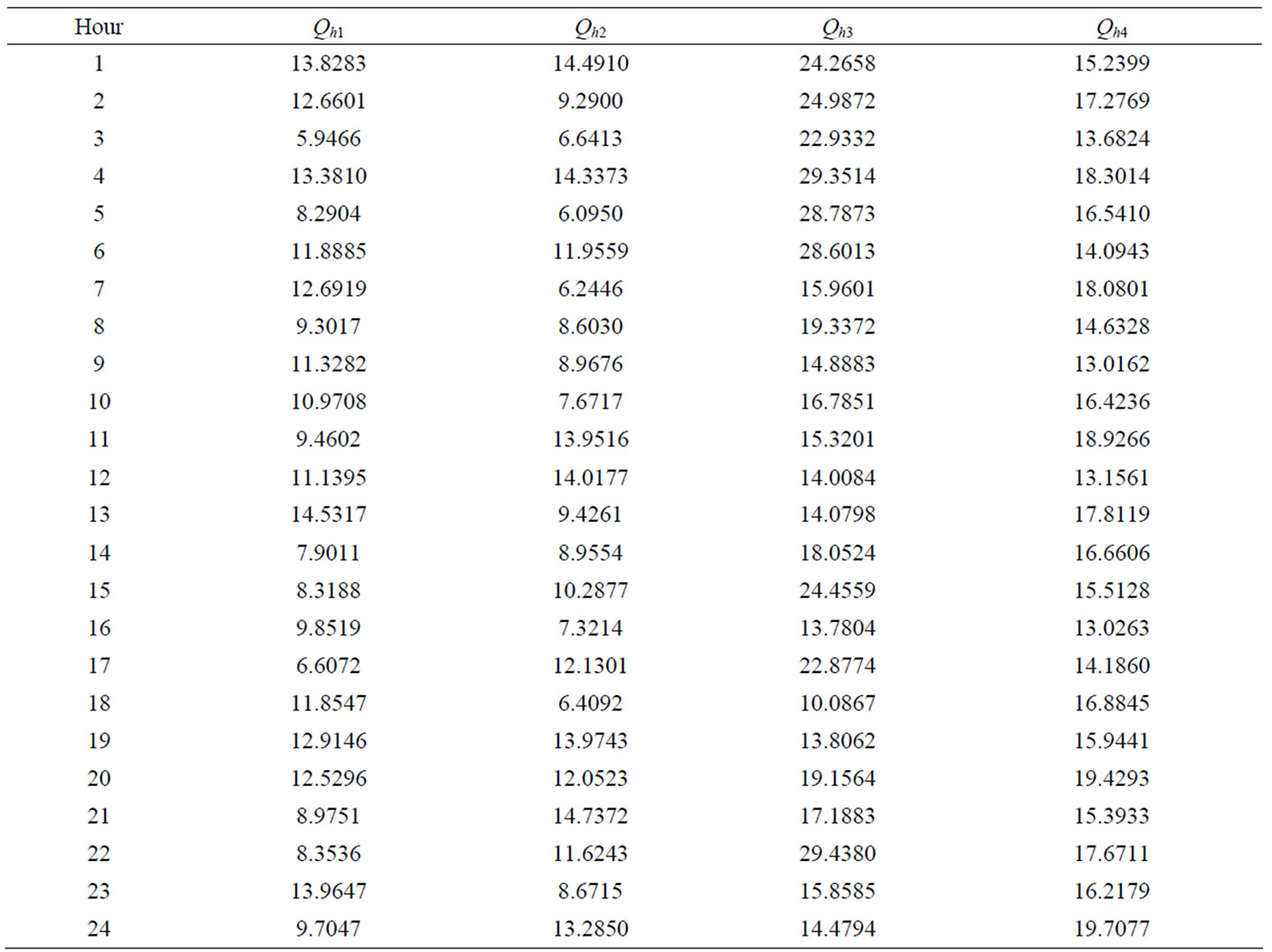
Table 1. Hourly discharge (×104 m3) for Test system-I using SOHPSO_TVAC.
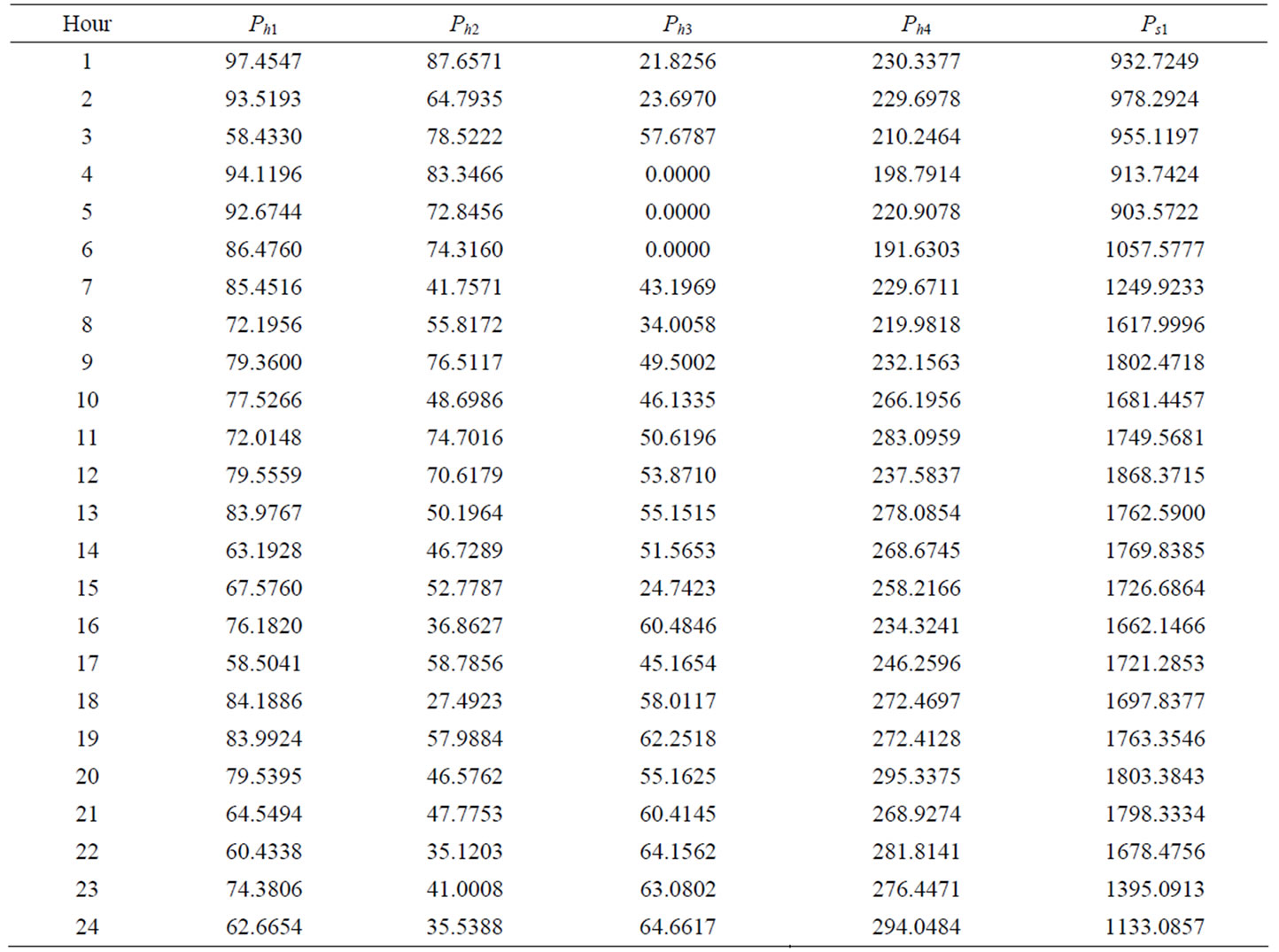
Table 2. Hydrothermal generation (MW) for Test System-I using SOHPSO_TVAC.
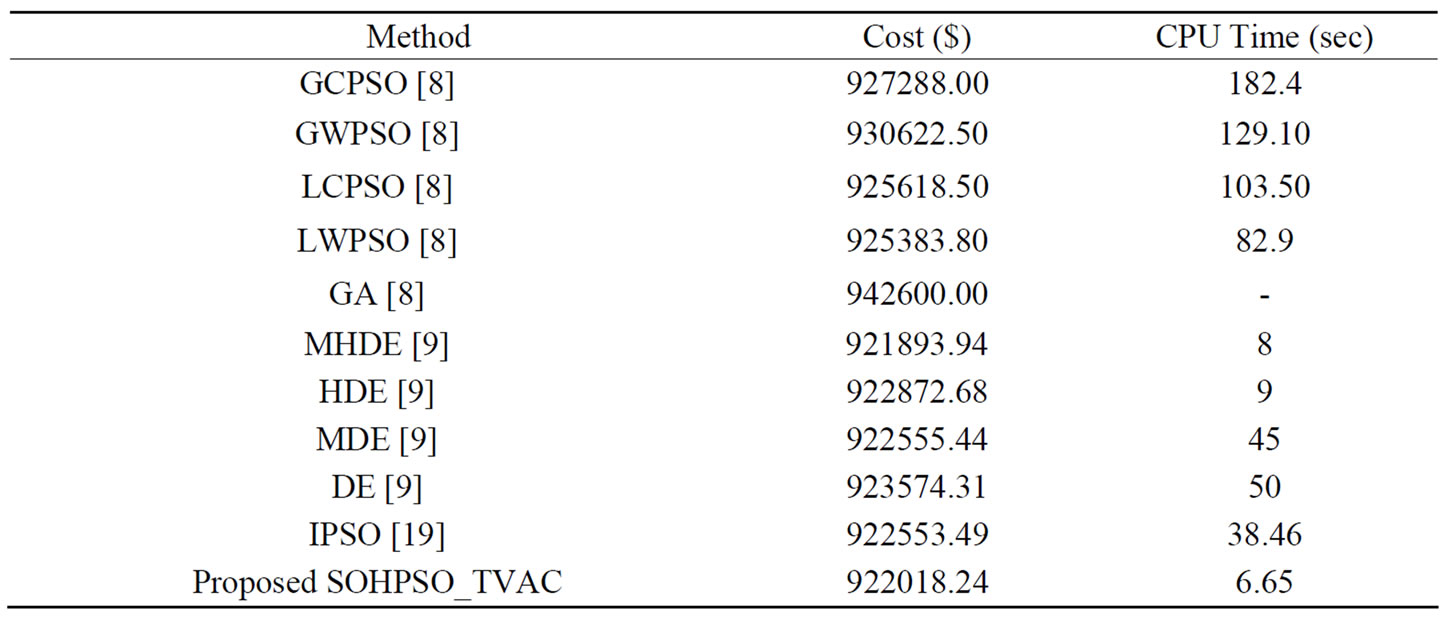
Table 3. Comparison of cost and Computation time [8,9,19] for Test System-I using SOHPSO_TVAC.
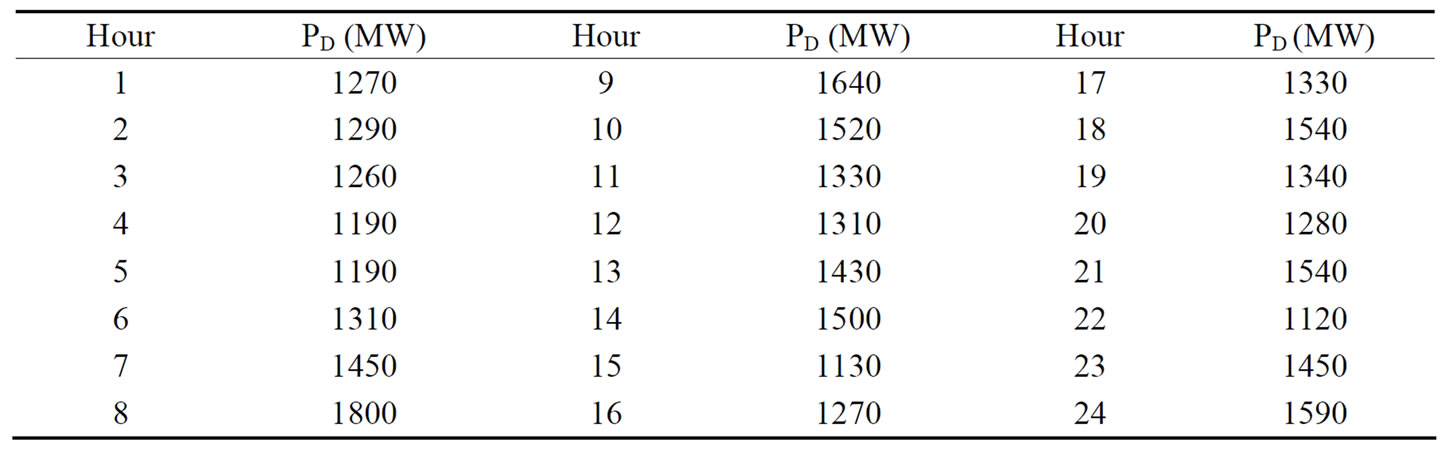
Table 4. Load demand for Test System-II.
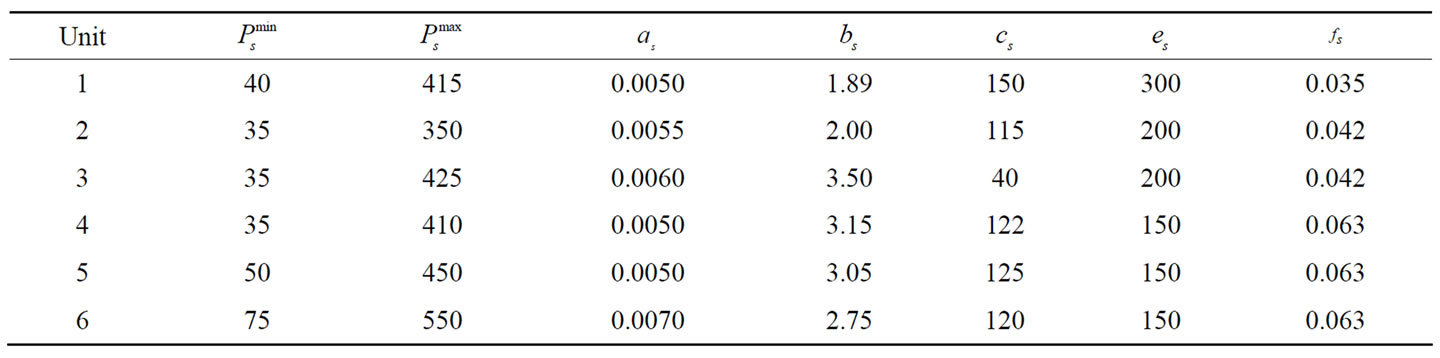
Table 5. Cost curve coefficients and operating limits of thermal generators for Test system-II.
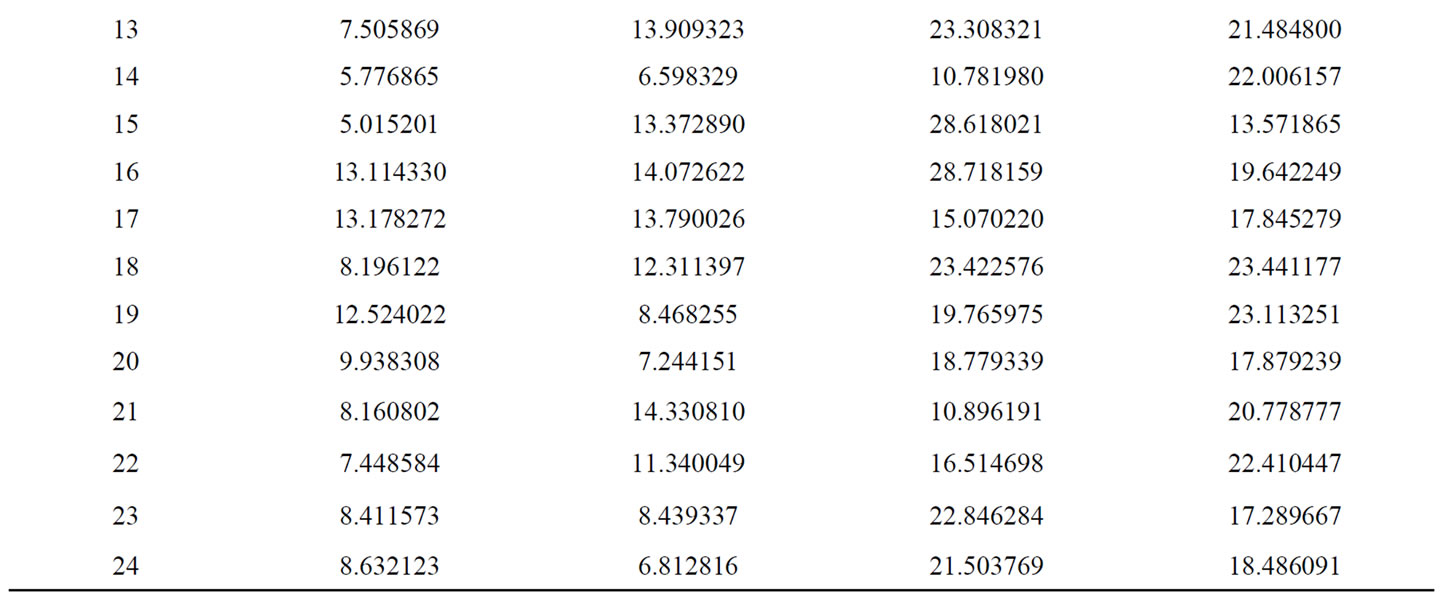
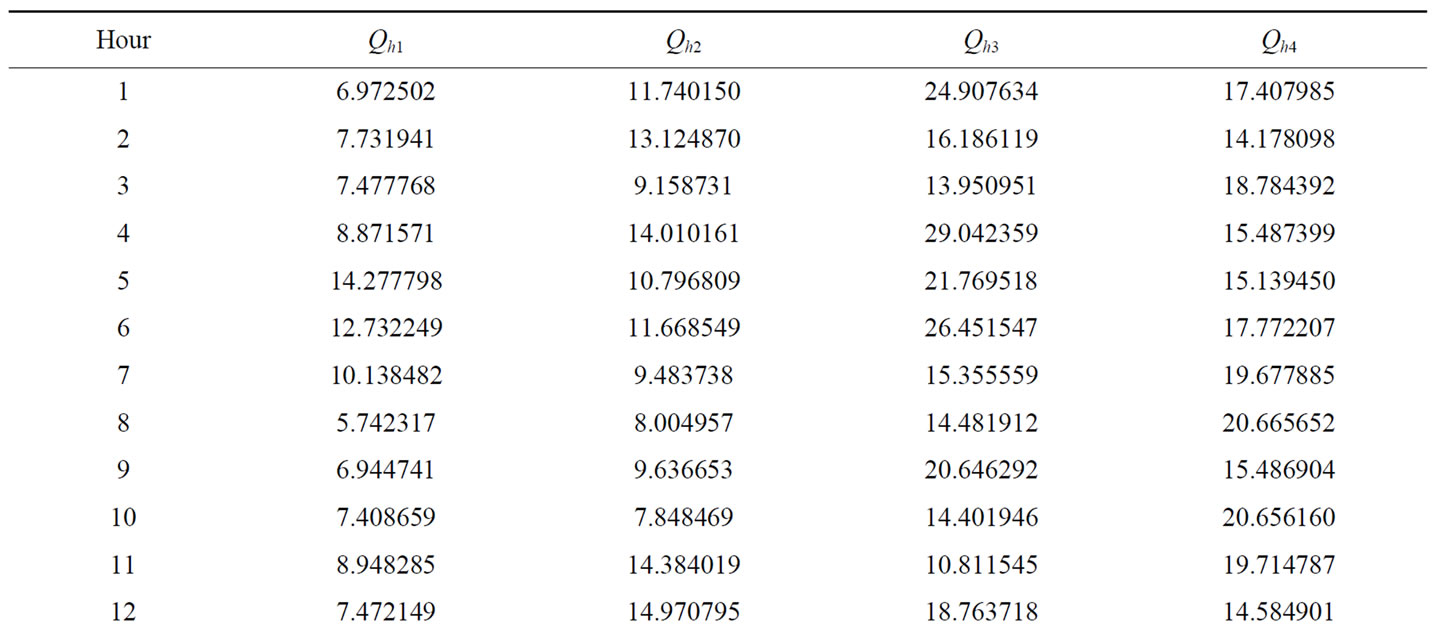
Table 6. Hourly plant discharge (×104 m3) for Test System-II for using SOHPSO_TVAC.
every scheduling interval. For example, total power (both hydro and thermal power) generated during hour 12 is 1310 MW while demand during the same interval is 1310 MW as seen in Table 4. Computation time for optimal solution for this case is found to be 76.25 seconds and optimal fuel cost is found to be $104232.48. The same problem was also solved by the so called classical PSO described in section 3.1. For this case optimal cost was found to be $106322.23. Figure 2 compares the convergence characteristic of fuel cost classical PSO and proposed SOHPSO_TVAC. It is clearly seen from the convergence characteristics that classical PSO converges to sub-optimal solution prematurely. It also seen that the proposed SOHPSO_TVAC algorithm successfully addresses the problem of premature convergence and produces better results.
6. Conclusions
Optimum scheduling of hydrothermal plants generation is of great importance to electric utilities. In this paper, a
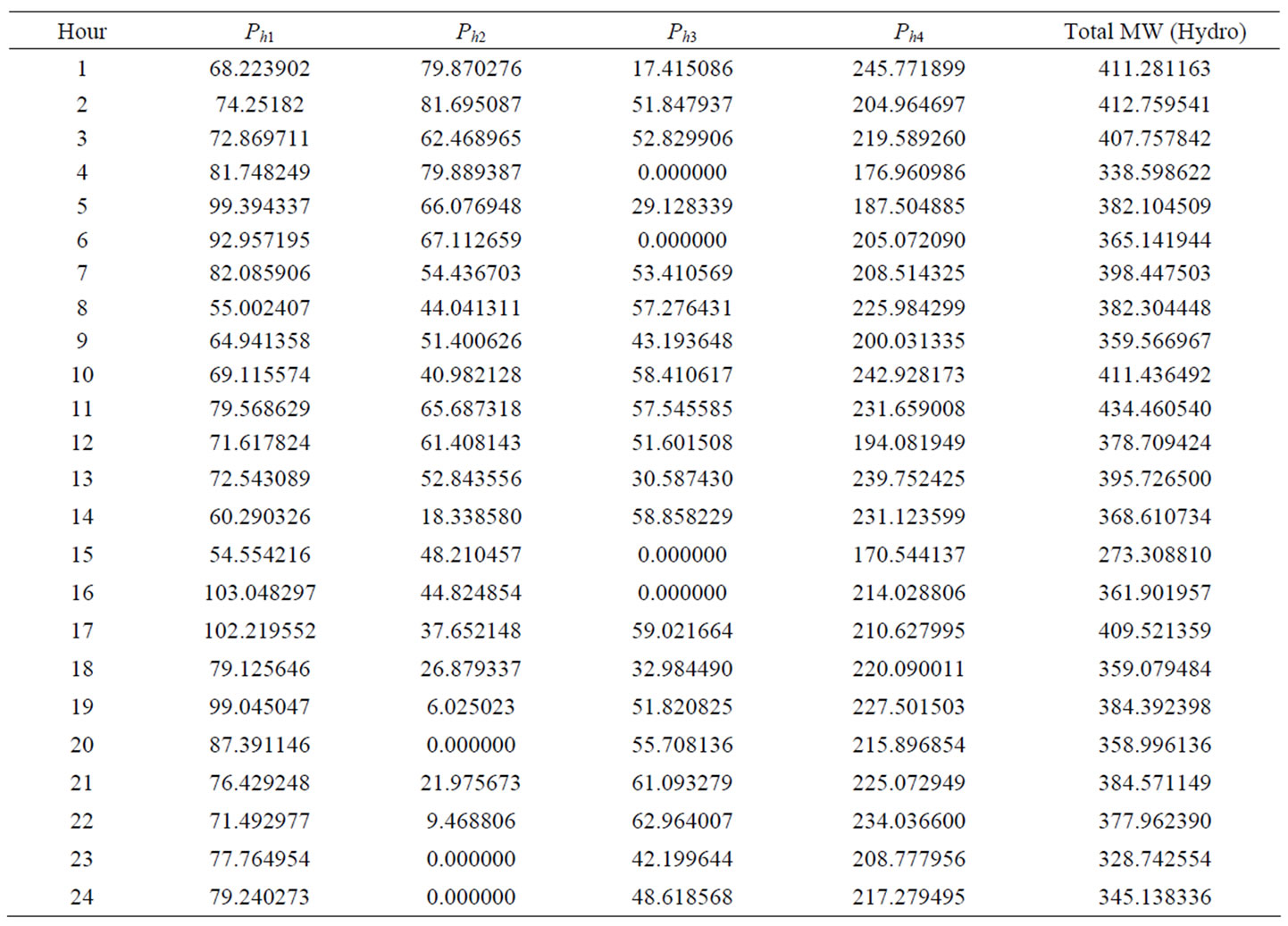
Table 7. Hydro Generation (MW) for Test System-II using SOHPSO_TVAC.

Table 8. Thermal Generation (MW) for Test System-II using SOHPSO_TVAC.
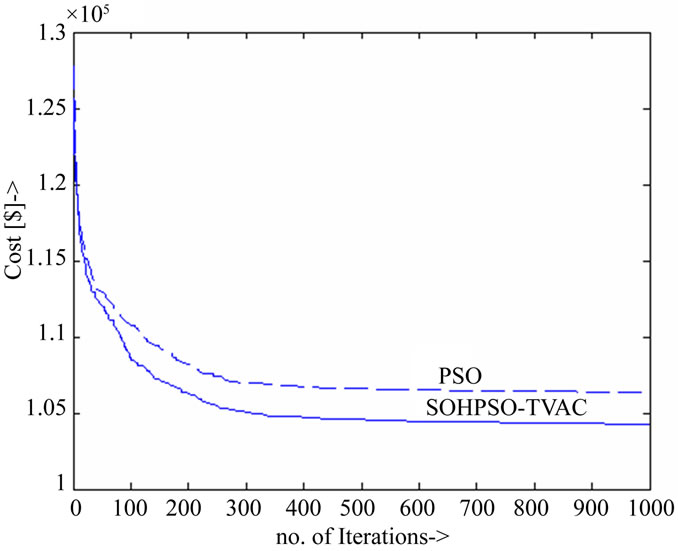
Figure 2. Convergence Characteristics for fuel cost.
novel algorithm called self-organizing hierarchical particle swarm optimization technique with time-varying acceleration coefficients (SOHPSO_TVAC) for solving short-term economic generation scheduling of hydrothermal systems to avoid premature convergence has been proposed and successfully applied to solve daily hydrothermal scheduling problem. To evaluate the performance of the proposed algorithm, it has been applied on two test systems comprising of a multi-chain cascade of hydro units and several thermal units and results are presented. The effect of valve point loading is also considered. The results obtained by the proposed method have been compared with other evolutionary algorithms like improved PSO, GA and modified hybrid differential evolution (MHDE). It is found that proposed method SOHPSO_TVAC can address the problem of premature convergence and produce better results.
7. Acknowledgments
We would like to acknowledge and thank Jadavpur University, Kolkata, India for providing all the necessary help to carry out this work.
REFERENCES
- H. Habibollahzadeh and J. A. Bubenko, “Application of Decomposition Techniques to Short Term Operation Planning of Hydro-Thermal Power System,” IEEE Transactions on Power Systems, Vol. 1, No. 1, February 1986, pp. 41-47. doi:org/10.1109/TPWRS.1986.4334842
- S. Chang, C. Chen, I. Fong and P. B. Luh, ‘Hydroelectric Generation Scheduling with an Effective Differential Dynamic Programming,” IEEE Transactions on Power Systems, Vol. 5, No. 3, 1990, pp. 737-743. doi:org/10.1109/59.65900
- R. F. Loyola and V. H. Quintana, “Medium-Term Hydrothermal Coordination by Semi Definite Programming”, IEEE Transactions on Power Systems, Vol. 18, No. 4, November 2003, pp. 1515-1522. doi:org/10.1109/TPWRS.2003.811006
- H. Brannud, J. A. Bubenko and D. Sjelvgren, “Optimal Short Term Operation Planning of a Large Hydrothermal Power System Based on a Non Linear Network Flow Concept,” IEEE Transactions on Power Systems, Vol. 1, No. 4, November 1986, pp. 75-82. http://dx.doi.org/10.1109/TPWRS.1986.4335019
- E. Gil, J. Bustos and H. Rudnick, “Short-Term Hydrothermal Generation Scheduling Model Using a Genetic Algorithm,” IEEE Transaction on Power Systems, Vol. 18, No. 4, November 2003, pp. 1256-1264. doi:org/10.1109/TPWRS.2003.819877
- K. P. Wong and Y. W. Wong, “Short-Term Hydrothermal Scheduling Part 1: Simulated Annealing Approach,” IEE Proceedings Generation, Transmission and Distribution, Vol. 141, No. 5, 1994, pp. 497-501. http://dx.doi.org/10.1049/ip-gtd:19941350
- P. C. Yang, H. T. Yang and C. L. Huang, “Scheduling Short-Term Hydrothermal Generation Using Evolutionary Programming Techniques,” IEE Proceedings Generation Transmission and Distribution, Vol. 143, No. 4, July 1996, pp. 371-376. doi:org/10.1049/ip-gtd:19960463
- B. H. Yu, X. H. Yuan and J. W. Wang, “Short-Term Hydro-Thermal Scheduling Using Particle Swarm Optimization Method,” Energy Conversion & Management, Vol. 48, No. 7, 2007, pp. 1902-1908. doi:org/10.1016/j.enconman.2007.01.034
- L. Lakshminarasimman and S. Subramanian, “A Modified Hybrid Differential Evolution for Short-Term Scheduling of Hydrothermal Power Systems with Cascaded Reservoirs,” Energy Conversion & Management, Vol. 49, No. 10, 2008, pp. 2513-2521. doi:org/10.1016/j.enconman.2008.05.021
- C.-T. Cheng, S.-L. Liao, Z.-T. Tang and M.-Y. Zhao, “Comparison of Particle Swarm Optimization and Dynamic Programming for Large Scale Hydro Unit Load Dispatch,” Energy Conversion & Management, Vol. 50, 2009, pp. 3007-3014. doi:org/10.1016/j.enconman.2009.07.020
- J. P. S. Catalão, H. M. I. Pousinho and V. M. F. Mendes, “Scheduling of Head-Dependent Cascaded Hydro Systems: Mixed-Integer Quadratic Programming Approach,” Energy Conversion & Management, Vol. 51, No. 3, 2010, pp. 524-530.
- J. Kennedy and R. Eberhart, “Particle Swarm Optimization,” Proceedings of IEEE International Conference on Neural Networks (ICNN’95), Perth, Australia, 27 November-1 December 1995, Vol. 5, pp. 2753-2756.
- Z.-L. Gaing, “Particle Swarm Optimization to Solving the Economic Dispatch Considering the Generator Constraints,” IEEE Transaction on Power Systems, Vol. 18, No. 3, August 2003, pp. 1187-1195. doi:org/10.1109/TPWRS.2003.814889
- M. A. Abido, “Optimal Design of Power-System Stabilizers Using Particle Swarm Optimization,” IEEE Transactions on Energy Conversion, Vol. 17, No. 3, September 2002, pp. 406-413. doi:org/10.1109/TEC.2002.801992
- J. B. Park, K.S. Lee, J. R. Shin and K.Y. Lee, “A Particle Swarm Optimization for Solving the Economic Dispatch With Non-smooth Cost Functions,” IEEE Transaction on Power Systems, Vol. 20, No.1, February 2005, pp. 34-42. doi:org/10.1109/TPWRS.2004.831275
- J. K. Wu, J. Q. Zhu, G. T. Chen and H. L. Zhang, “A Hybrid Method for Optimal Scheduling of Short-Term Electric Power Generation of Cascaded Hydroelectric Plants Based on Particle Swarm Optimization and Chance-Constrained Programming,” IEEE Transaction on Power Systems, Vol. 23, No. 4, November 2008, pp. 1570-1579. doi:org/10.1109/TPWRS.2008.2004822
- A. Ratnaweera, S. K. Halgamuge and H. C. Watson, “Self-Organizing Hierarchical Particle Swarm Optimizer with Time-Varying Acceleration Coefficients,” IEEE Transactions on Evolutionary Computation, Vol. 8, No. 3, June 2004, pp. 240-255. doi:org/10.1109/TEVC.2004.826071
- Y. Shi and R. C. Eberhart, “Parameter Selection in Particle Swarm Optimization, Lecture Notes in Computer Science—Evolutionary Programming,” Proceedings of the 7th International Conference on Evolutionary Programming, San Diego, 25-27 March 1998, Vol. 1447, pp. 591-600.
- P. K. Hota, A. K. Barisal and R. Chakrabarti, “An improved PSO Technique for Short-Term Optimal Hydrothermal Scheduling,” Electric Power Systems Research, Vol. 79, No. 7, 2009, pp. 1047-1053. doi:org/10.1016/j.epsr.2009.01.001
Appendix A: List of Symbols
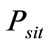 : output power of
: output power of 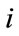 th thermal unit at time
th thermal unit at time 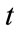
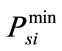 ,
,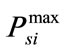 : lower and upper generation limits for
: lower and upper generation limits for 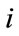 th thermal unit
th thermal unit
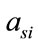 ,
, 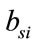 ,
, 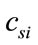 ,
, 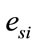 ,
, : cost curve coefficients of
: cost curve coefficients of 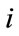 th thermal unit
th thermal unit
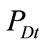 : load demand at time
: load demand at time 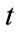
 : output power of j-th hydro unit at time
: output power of j-th hydro unit at time 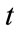
 ,
,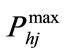 : lower and upper generation limits for
: lower and upper generation limits for 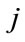 th hydro unit
th hydro unit
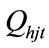 : water discharge rate of j-th reservoir at time
: water discharge rate of j-th reservoir at time 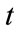
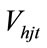 : storage volume of j-th reservoir at time
: storage volume of j-th reservoir at time 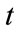
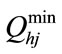 ,
,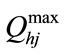 : minimum and maximum water discharge rate of j-th reservoir
: minimum and maximum water discharge rate of j-th reservoir
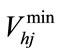 ,
,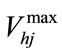 : minimum and maximum storage volume of
: minimum and maximum storage volume of 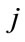 th reservoir
th reservoir
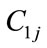 ,
, 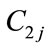 ,
,  ,
, 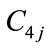 ,
, 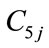 ,
,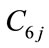 : power generation coefficients of j-th hydro unit
: power generation coefficients of j-th hydro unit
 : inflow rate of
: inflow rate of 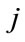 th reservoir at time
th reservoir at time 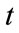
 : number of upstream units directly above
: number of upstream units directly above 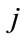 th hydro plant
th hydro plant
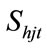 : spillage of
: spillage of 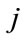 th reservoir at time
th reservoir at time 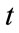
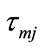 : water transport delay from reservoir
: water transport delay from reservoir ![]() to j
to j
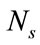 : number of thermal generating units
: number of thermal generating units
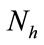 : number of hydro generating units
: number of hydro generating units

