Journal of Modern Physics
Vol.4 No.1(2013), Article ID:27018,4 pages DOI:10.4236/jmp.2013.41011
Mysteries of Granular Planet
Komsomolsk-on-Amur State Technical University, Komsomolsk-on-Amur, Russia
Email: m_skachkov@list.ru
Received July 24, 2012; revised October 26, 2012; accepted November 9, 2012
Keywords: Granular Media; Gravitating Ball; Self-Organization; Mesoscopic State; Phase Transition; Stresses Radial Distribution
ABSTRACT
The behavior of self-organizing granular medium in its own gravitational field is considered. The study is led within an approach proposing the existence of only three types of mesoscopic states in the material: so named hydrostatic, columnar and arched mesoscopic states. The results of this study are not obvious. Indeed, in the center of granular gravitating ball, as it turns out, pressure may be absent, though it is well-known that the pressure in either non-compressible liquid or solid linear-elastic medium is maximal. Such an uncommon stress state takes place at the arched mesoscopic state. Using the Mohr-Coulomb condition has given that the arched state can embody when sinus of internal friction’s angle increases up to the threshold value 1/3. At the hydrostatic mesoscopic state granular medium is like a liquid. The study also has shown the transition between hydrostatic and non-hydrostatic stress states being sharp in granular gravitating ball that opposes the known results of the linear theory of elasticity. At the columnar mesoscopic state any gravitating granular ball cannot be.
1. Introduction
If a certain planet was composed of non-cohesive granular material, it should behave in unexpected ways.
Granular medium possesses a series of remarkable properties. A part of them makes it similar to other basic classes of substance: solids, liquids and gases. And the other part, including various self-organization phenomena, is unique. Today much of the latter is reflected in the concept of granular chains [1,2].
Previously a continuum model of non-cohesive granular media taking into account their ability to compressing and self-organizing was suggested [3-7]. The model works well in wide range of materials and loads. It describes adequately both natural porous materials with hydrostatic stress state in the Earth’s gravitational field [3], and nanopowders with non-hydrostatic stress state in cylindrical tubes under superficial radial load [4]. The model results have agreed well with the in situ measurements on carbonate rocks down to 5500 m and on snow banks to 10 m thick, and the laboratory measurements on nano-sized powders in capsules of 0.015 m under the GPa order pressure. These arguments allow hoping that the predictions about self-organizing granular body in its own gravitational field will be confirmed too.
A theme of finding stress state for gravitating ball is sufficiently traditional for various branches of mechanics and physics. So, it has solved within the classical elastic theory in displacements [8,9]. It has solved for a perfect Pascal fluid in 4D space-time [10]. And also it has already solved within the suggested model for weak-compressible granular medium at hydrostatic stress state [6].
One of the initial model’s hypotheses is the assumption of existence possibility in granular medium only three types of mesoscopic state, called hydrostatic, columnar and arched ones. At the hydrostatic mesoscopic state there is no an order. Two types of order are embodied by the columnar and arched states. These ordered states may be discussed using the terms of granular chains by the following way: At the columnar state the most chains act as columns bearing the longitudinal compressing load; at the arched state the most chains act as arches bearing the lateral straightening load. It is obvious that the granular chains acting by such a way can be stable only at presence of friction between the granules composing them. The choice of a mesoscopic state’s type seems to be embodied by self-organization process whose attractors are still not fully understood.
One of the most important constitutive relations deduced from the hypotheses is linear coupling of the stress tensor principal components’ values, which possesses at spherical symmetry the form
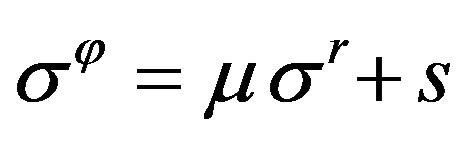 . (1)
. (1)
Here 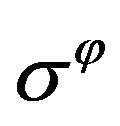 and
and  are the circumferential and radial stresses, taken positive in compression;
are the circumferential and radial stresses, taken positive in compression; 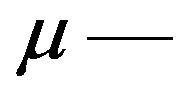 a constant of given mesoscopic state’s type, called mesoscopic factor, independent on given material and load’s intensity; and
a constant of given mesoscopic state’s type, called mesoscopic factor, independent on given material and load’s intensity; and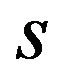 —a constant of given loaded body.
—a constant of given loaded body.
For the mesoscopic factor the spectrum of values has been deduced [7]. The following values characterize in 3D space columnar, hydrostatic and arched mesoscopic states, respectively:
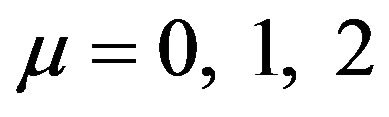 ; (2)
; (2)
besides, of course, at the hydrostatic state .
.
In 2D space the spectrum, analogical to spectrum (2), is
 .
.
2. The Problem Statement
Within the model represented we find the stress state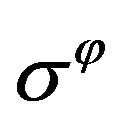 ,
, 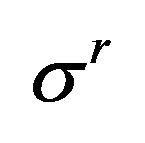 for granular gravitating ball of external radius
for granular gravitating ball of external radius 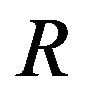 without superficial loading. Let
without superficial loading. Let 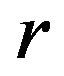 denote the current polar radius, then
denote the current polar radius, then ,
,  , and
, and
 . (3)
. (3)
We take the assumptions being usual for granular media’s continual mechanics at similar problems statement:
1) The medium is non-compressible;
2) The Mohr-Coulomb limiting yield condition is valid: Alpha
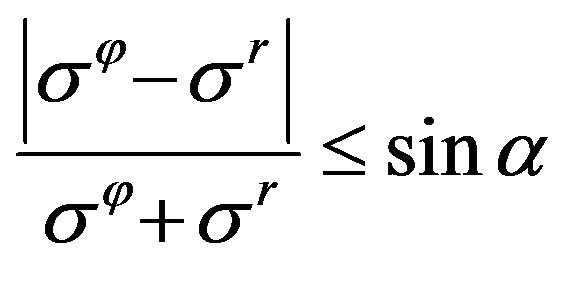 where
where 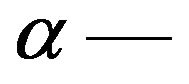 the angle of internal friction,
the angle of internal friction,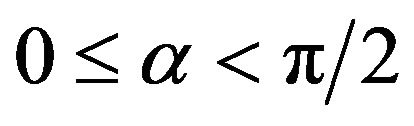 ;
;
3) The stresses as functions of the radius have no breaks.
It is true the following differential equilibrium equation written in stresses for gravitating ball of non-compressible material, or of material with heterogenic density distribution, according to the Newtonian potential theory [8,9]:
 , (4)
, (4)
where 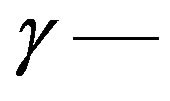 the universal gravitational constant,
the universal gravitational constant,  is the density.
is the density.
So, the problem is to find the functions ,
, 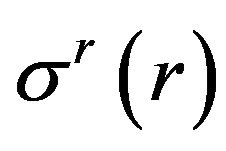 satisfying both the system (1), (4) with boundary condition (3) and the Mohr-Coulomb condition. Moreover, in such a way we must iterate through all types of mesoscopic state.
satisfying both the system (1), (4) with boundary condition (3) and the Mohr-Coulomb condition. Moreover, in such a way we must iterate through all types of mesoscopic state.
The Mohr-Coulomb condition and the boundary condition for radial stress (3) determine also the boundary condition for circumferential stress:
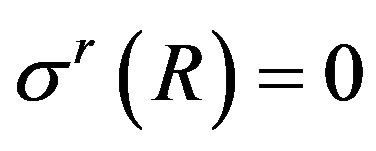 .
.
From here the value of additive parameter of Formula (1) follows:
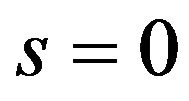 .
.
Hence Formula (1) takes the form
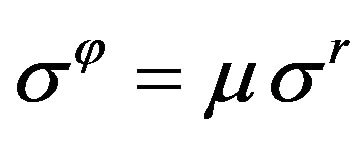 . (5)
. (5)
3. Columnar State
In accordance with Formula (2), at columnar type of mesoscopic state
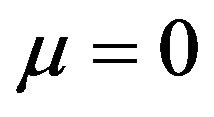 then because of formula (5) the Mohr-Coulomb condition becomes unattainable. Indeed, the obvious require ment
then because of formula (5) the Mohr-Coulomb condition becomes unattainable. Indeed, the obvious require ment 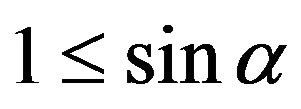 can be satisfied only at limit case of
can be satisfied only at limit case of 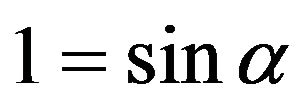 which would imply the presence of cohesion in the material contrary to the model’s initial principles. Morefore the solution of the system (1), (4) would imply the presence of non-removable singularity in the origin.
which would imply the presence of cohesion in the material contrary to the model’s initial principles. Morefore the solution of the system (1), (4) would imply the presence of non-removable singularity in the origin.
It points to the impossibility of implementing columnar state at gravitating granular ball.
4. Hydrostatic State
At the case of hydrostatic mesoscopic state in which 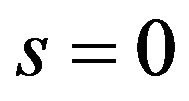 and according to Formula (2)
and according to Formula (2)
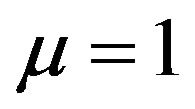 our study turns into the classical problem on the pressure of rigid or liquid gravitating ball having the well-known solution for pressure
our study turns into the classical problem on the pressure of rigid or liquid gravitating ball having the well-known solution for pressure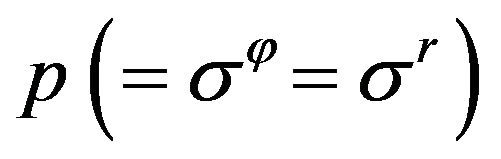 , obtained from Equation (4):
, obtained from Equation (4):
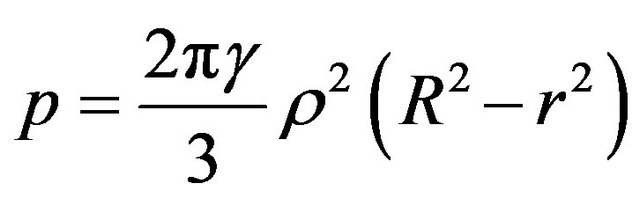 . (6)
. (6)
The found function 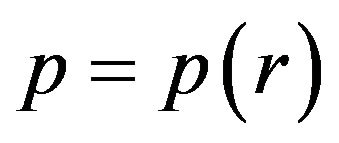 is shown by Figure 1. It is obvious, that
is shown by Figure 1. It is obvious, that
 . (7)
. (7)
The Mohr-Coulomb condition 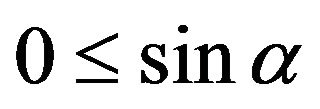 introduces no restrictions on implementing hydrostatic state.
introduces no restrictions on implementing hydrostatic state.
5. Arched State
It is the arched state where granular medium behaves in unexpected ways. At this type of mesoscopic state in accordance with formula (2)
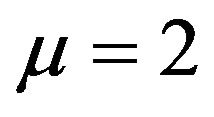 and formula (5) is written as
and formula (5) is written as
 . (8)
. (8)
Competition of this ratio and the requirement of symmetry or the equality of directions at the origin

gives rise to a property which can be named as the 1st mystery of granular planet: in the arched mesoscopic state pressure in the center does not exist, i.e.
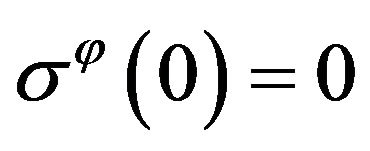 ,
,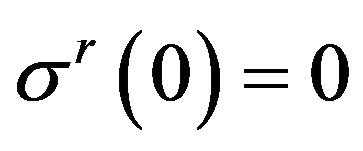 .
.
This particularity is demonstrated by Figure 1. It is impotent to emphasize that the suggested model has already predicated a similar effect of reducing the stresses toward the center for arched granular ball under only superficial radial load [5].
Now we consider the stress distribution over the thickness of granular planet. Substituting coupling (8) into Equation (4) we have:
 .
.
The integral of the obtained equation, satisfying the boundary condition (3), is expressed through elementary functions:
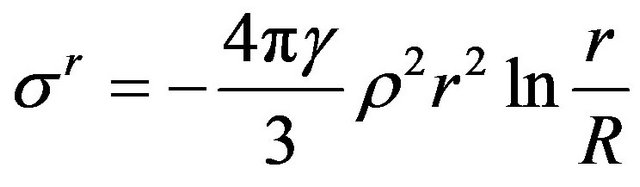 . (9)
. (9)
And, owing to coupling (8),
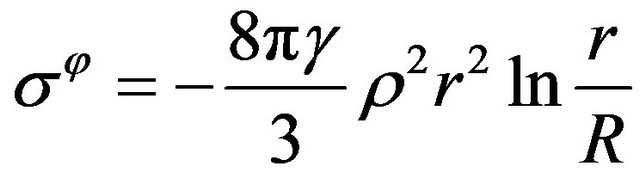 . (10)
. (10)
The found functions ,
, 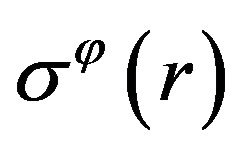 have removable singularities in the origin. Indeed, from results (9) and (10) we can see:
have removable singularities in the origin. Indeed, from results (9) and (10) we can see:
 .
.
The obtained stresses distribution is shown by Figure 1. From analysis of the found solution we can see, that
 ,
,
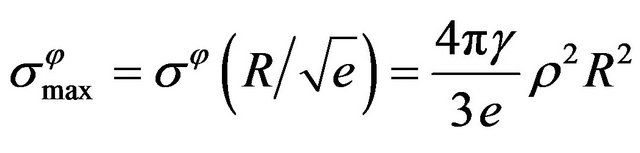 .
.
Hence, taking into account result (7),
 ,
,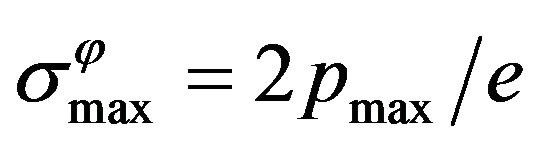 .
.
The curves  and
and  have inflection points at
have inflection points at
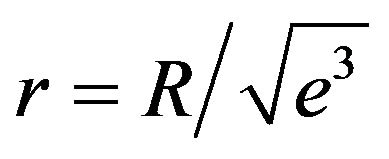 .
.
According to the Mohr-Coulomb condition, arched state can embody only at sufficiently high internal friction: , or
, or
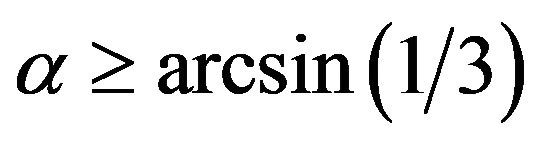 . (11)
. (11)
6. Transition between Hydrostatic and Arched States
We can see from result (11) that at 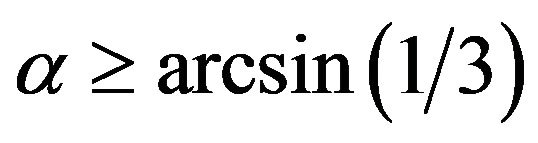 the both mesoscopic states, hydrostatic and arched, are allowed. So the question arises: to what type of mesoscopic state the self-organization process is to direct? A similar question has been just studied within the suggested model when considering compressible granular ball under superficial load [5]. And the proposition has been done that the attractor of self-organizing is minimization of the external forces mechanical work. Calculation of the work at two the mesoscopic states has given that its value at arched state is less than at hydrostatic.
the both mesoscopic states, hydrostatic and arched, are allowed. So the question arises: to what type of mesoscopic state the self-organization process is to direct? A similar question has been just studied within the suggested model when considering compressible granular ball under superficial load [5]. And the proposition has been done that the attractor of self-organizing is minimization of the external forces mechanical work. Calculation of the work at two the mesoscopic states has given that its value at arched state is less than at hydrostatic.
As mentioned above, today the self-organization attractors in granular medium are not still fully understood. But in any case, if arched type of mesoscopic state was more profitable than hydrostatic one for gravitating granular ball, then at achieving the internal friction’s
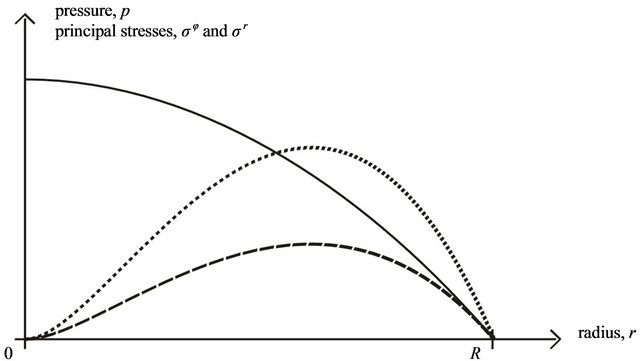
Figure 1. Qualitative diagram of stresses distribution over the radius for two types of mesoscopic state in granular gravitating ball with external radius R. Pressure p (solid line) describes the stress state corresponding to hydrostatic mesoscopic state, valid at low internal friction; circumferential stress σφ (dots) and radial stress σr (dashes) describe the stress state corresponding to arched mesoscopic state, valid at high internal friction.
angle up to the value of 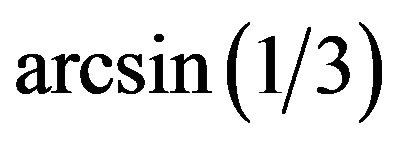 the pressure expressed with Equation (6) must be replaced by the stresses expressed with Equations (9) and (10).
the pressure expressed with Equation (6) must be replaced by the stresses expressed with Equations (9) and (10).
For quantitative analyzing parameters changed at the transition let us use the average stress  and maximum shear stress
and maximum shear stress 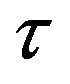 [9]:
[9]:
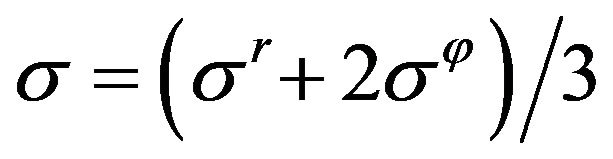 ,
,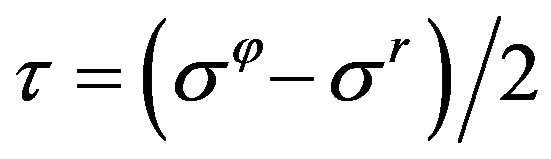 .
.
It is obvious that at hydrostatic state ,
,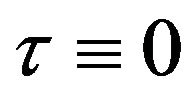 . The greatest drop of the average stress takes place in the ball’s center: from the maximal pressure’s value
. The greatest drop of the average stress takes place in the ball’s center: from the maximal pressure’s value 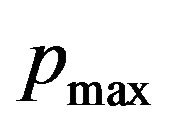 down to zero. The greatest jump of the maximum shear stress takes place at
down to zero. The greatest jump of the maximum shear stress takes place at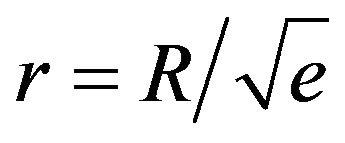 : from zero up to the value
: from zero up to the value
 .
.
So the threshold value 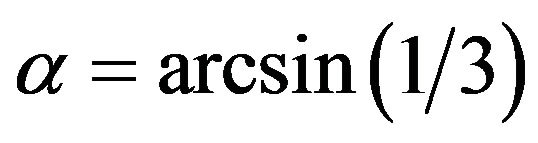 may be discussed as a point of bifurcation. Such a sharp transition between stress states opposes gravitating ball of granular material at one hand and of linear-elastic material at another. Because according to the linear theory of elasticity, such a transition in gravitating ball goes smoothly with changing the Poisson coefficient [8,9]. Going in granular ball sharply, such a transition between two mesoscopic states and two stress states, being undoubtedly a phase one, can be named as the 2nd mystery of granular planet.
may be discussed as a point of bifurcation. Such a sharp transition between stress states opposes gravitating ball of granular material at one hand and of linear-elastic material at another. Because according to the linear theory of elasticity, such a transition in gravitating ball goes smoothly with changing the Poisson coefficient [8,9]. Going in granular ball sharply, such a transition between two mesoscopic states and two stress states, being undoubtedly a phase one, can be named as the 2nd mystery of granular planet.
Presence of this sharp inter-state transition is caused with the accepted assumption of stresses as functions of the radius having no breaks. Due to this assumption granular planet’s stresses change at  by a jump and do not depend on internal friction at other values of
by a jump and do not depend on internal friction at other values of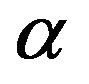 . If we refused the assumption, we might propose existence possibility of a complex stress state with two domains of two different mesoscopic and stress states; and the size of a spherical board between these domains would smoothly change during changing
. If we refused the assumption, we might propose existence possibility of a complex stress state with two domains of two different mesoscopic and stress states; and the size of a spherical board between these domains would smoothly change during changing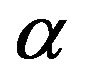 .
.
7. Conclusions
We have considered granular gravitating ball within a new continual model of compressible self-organizing granular medium at its limit case of incompressibility and using the Mohr-Coulomb limiting yield condition.
We have found exact expressions in the elementary functions for the body’s stresses in all considered cases. Our study has given a non-evident result. In-first, the pressure in the center of the ball can absent. In-second, the stresses are able to change at the threshold value of internal friction’s angle 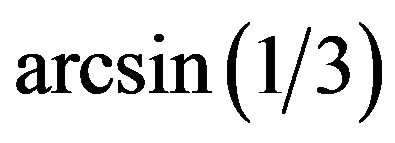 by a jump and not to depend on it at other values.
by a jump and not to depend on it at other values.
It seems that taking into account the effect of compressibility cannot involve qualitative changes into the results reported.
Now we are in waiting for empirical data being to verify our attempt of theoretical predicting.
REFERENCES
- R. Behringer, H. Jaeger and S. Nagel, “Introduction to the Focus Issue on Granular Materials,” Chaos, Vol. 9, No. 3, 1999, pp. 509-510. doi:10.1063/1.166426
- M. E. Cates, J. P. Wittmer, J.-P. Bouchaud and P. Claudin, “Jamming and Static Stress Transmission in Granular Materials,” Chaos, Vol. 9, No. 3, 1999, pp. 511-522. doi:10.1063/1.166456
- M. N. Skachkov, “Density and Pressure in Granular Media in the Gravity Field,” Journal of Mining Science, Vol. 47, No. 1, 2011, pp. 30-36. doi:10.1134/S1062739147010047
- M. N. Skachkov, “Compression of Plane Ring or Cylindrical Granular Layer with Fixed Inner Boundary,” Transactions of Symposium on Science, Education and Technologies, Komsomolsk-on-Amur, 26-28 October 2010, pp. 180-183.
- M. N. Skachkov, “Nontrivial Solution to the Equilibrium Problem of a Granular Globe with Low Friction,” Proceedings TulSU. Natural Scienses, No. 2, 2010, pp. 109- 115.
- M. N. Skachkov, “The Equilibrium of Granular Gravitating Ball,” Bulletin KnASTU, No. 13, 2009, pp. 235- 237.
- M. N. Skachkov, “The Conformational States of Granular Materials,” Bulletin KnASTU, No. 13, 2009, pp. 238-240.
- L. D. Landau and E. M. Lifshitz, “Theory of Elasticity,” 5th Edition, Butterworth-Heinemann, Oxford, 1986.
- A. I. Lurie, “Theory of Elasticity,” Springer, Berlin, 2005. doi:10.1007/978-3-540-26455-2
- A. M. Baranov and R. V. Bikmurzin, “Exact Static Solutions for Fluid Gravitating Balls in Homogeneous Coordinates,” Gravitating and Cosmology, Vol. 12, No. 2-3, 2006, pp. 103-105.

