ABSTRACT

A Walker n-manifold is a semi-Riemannian n-manifold, which admits a field of parallel null r-planes, with r ≤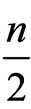. It is well-known that semi-Riemannian geometry has an important tool to describe spacetime events. Therefore, solutions of some structures about 4-Walker manifold can be used to explain spacetime singularities. Then, here we present complex and paracomplex analogues of Lagrangian and Hamiltonian mechanical systems on 4-Walker manifold. Finally, the geometrical-physical results related to complex (paracomplex) mechanical systems are also discussed.

1. Introduction

As is well known, modern differential geometry plays an important role to explain the dynamics of Lagrangians. So, if Q is an m-dimensional configuration manifold and 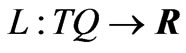is a regular Lagrangian function, then it is well-known that there is a unique vector field X on TQ such that dynamics equation is given by

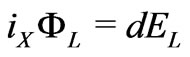(1)

where 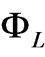indicates the symplectic form. The triple (TQ, 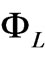, X) is called a Lagrangian system on the tangent bundle TQ.

Also, modern differential geometry provides a good framework in which develop the dynamics of Hamiltonians. Therefore, if Q is an m-dimensional configuration manifold and is a regular Hamiltonian energy function, then there is a unique vector field X on T^*Q such that dynamics equation is given by

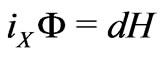(2)

where Φ indicates the symplectic form. The triple (T^*Q, Φ, X) is called a Hamiltonian system on the cotangent bundle T^*Q.

Nowadays, there are many studies about Lagrangian and Hamiltonian dynamics, mechanics, formalisms, systems and equations [1-5] and there in. There are real, complex, paracomplex and other analogues. As we know it is possible to produce different analogues in different spaces.

Let be a Riemannian manifold with a neutral metric, i.e. with a semi-Riemannian metric g of signature (n, n). By a Walker n-manifold, we mean a semi-Riemannian manifold which admits a field of parallel null r-planes, with 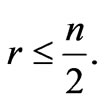The canonical forms of the metrics were investigated by Walker [6]. Special interest manifolds are Walker manifolds of even dimensions (n = 2m) admitting a field of null planes of maximum dimensionality (r = m). An application of such a 4-dimensional Walker metric is given in [7]. Since the observation of the existence of almost complex structure on Walker 4-manifolds in [8], the Walker 4-manifolds and the almost Hermitian structures on the four-manifolds have been intensively studied, e.g., [9-14], etc. In this study, we present complex (paracomplex) analogues of Lagrangian and Hamiltonian mechanical systems on 4-Walker manifold. In the end, some geometrical-physical results about the obtained complex (paracomplex) mechanical systems are also given.

Throughout this paper, all mathematical objects and mappings are assumed to be smooth, i.e. infinitely differentiable and Einstein convention of summarizing is adopted. Denote by 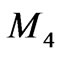a Walker manifold. Then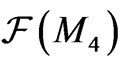, and 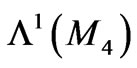are the set of functions on M₄, the set of vector fields on M₄ and the set of 1-forms on M₄, respectively.

2. Walker Manifold M₄

2.1. Walker Metric

A neutral metric g on a 4-manifold M₄ is said to be Walker metric if there exists a 2-dimensional null distribution D on M₄, which is parallel with respect to g. From Walker theorem [6], there is a system of coordinates with respect to which g takes the local canonical form

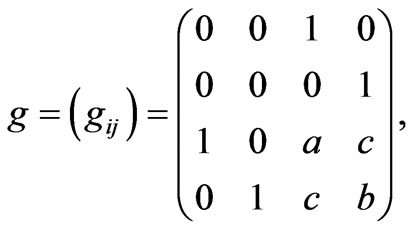(3)

where a, b, c are smooth functions of the coordinates (x₁, x₂, x₃, x₄). The parallel null 2-plane D is spanned locally by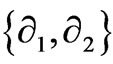, where 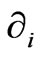are the abbreviated forms of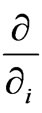i = x₁, x₂, x₃, x₄.

2.2. Proper Almost Complex Structure φ

Let φ be a proper almost complex structure on a Walker manifold M₄, which satisfies

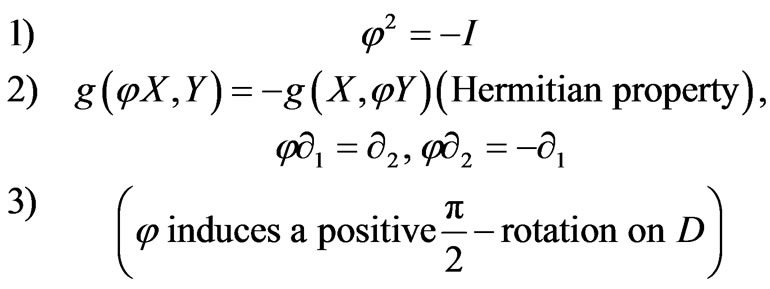
We easily see that the above three properties defines φ uniquely, i.e.

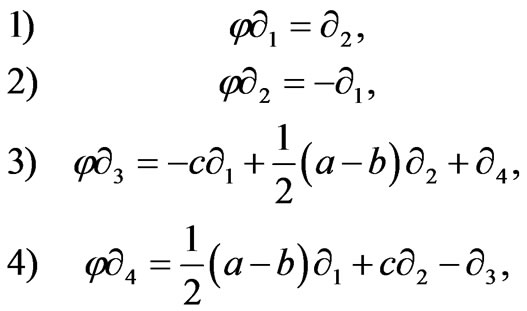(4)

If we write as 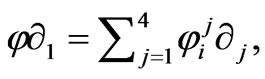then from (4) we can read off the nonzero components 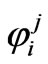as follows:

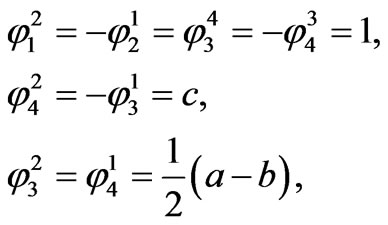
i.e., has the local components

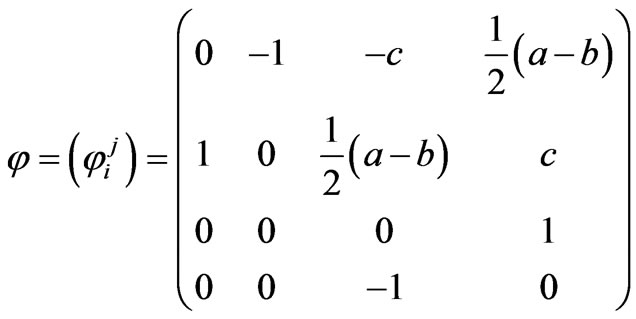
with respect to the natural frame [14].

Similarly, we define a unique proper almost complex structure 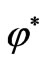as follows:

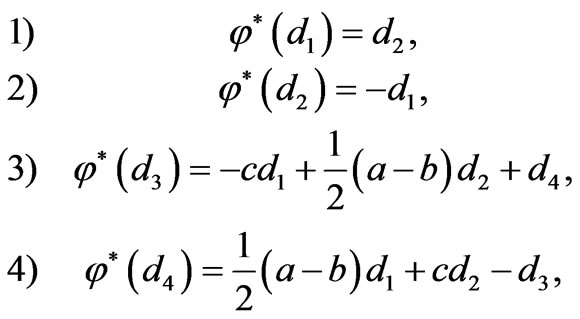(5)

where d_i are the abbreviated forms of dx_i, i = x₁, x₂, x₃, x₄.

3. Lagrangian Mechanical Systems

Now, our purpose is to obtain complex Euler-Lagrange equations for relativistic, quantum and classical mechanics on 4-dimensional Walker manifold M₄.

Let M₄ be a Walker manifold and {x₁, x₂, x₃, x₄} be its coordinate functions. Let the semispray be the vector field X determined by

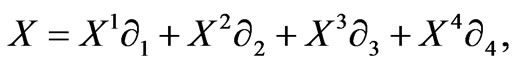(6)

where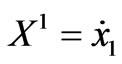, , 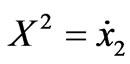, 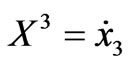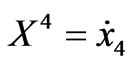and the dot indicates the derivative with respect to time t. By means of the proper almost complex structure φ given by (4), the vector field is defined by

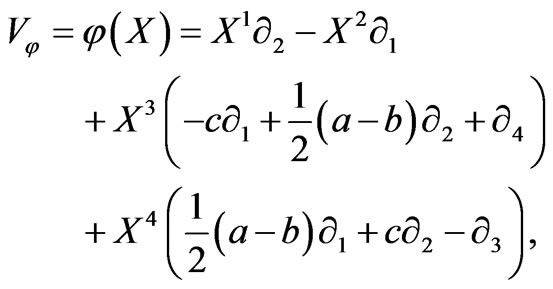
which is named Liouville vector field on the Walker manifold M₄. The maps given by 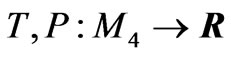such that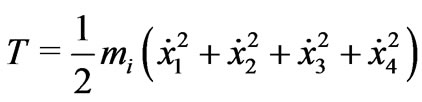, 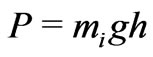are said to be the kinetic energy and the potential energy of the system, respectively. Here m_i, g and h stand for mass of a mechanical system having m particles, the gravity acceleration and distance to the origin of a mechanical system on Walker manifold M₄, respectively. Then 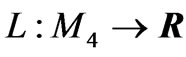is a map that satisfies the conditions; 1) 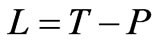is a Lagrangian function, 2) the function determined by 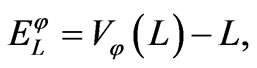is energy function.

The function induced by and denoted by

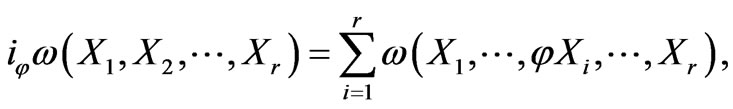
is called vertical derivation, where 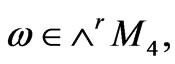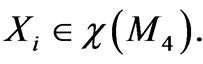The vertical differentiation is given by

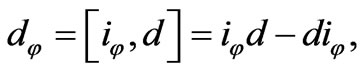
where d is the usual exterior derivation. For the almost complex structure given by (4), the form on Walker manifold M₄ is the closed 2-form determined by 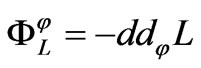such that

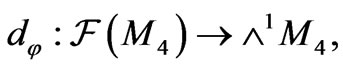
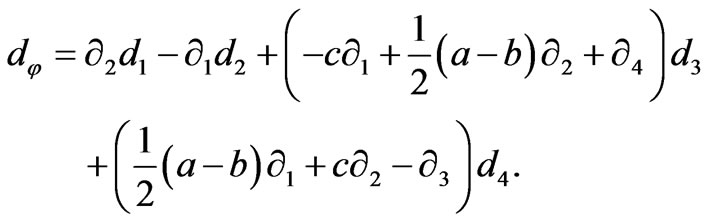(7)

Through a direct computation using (7), the closed 2- form is seen to be as follows:

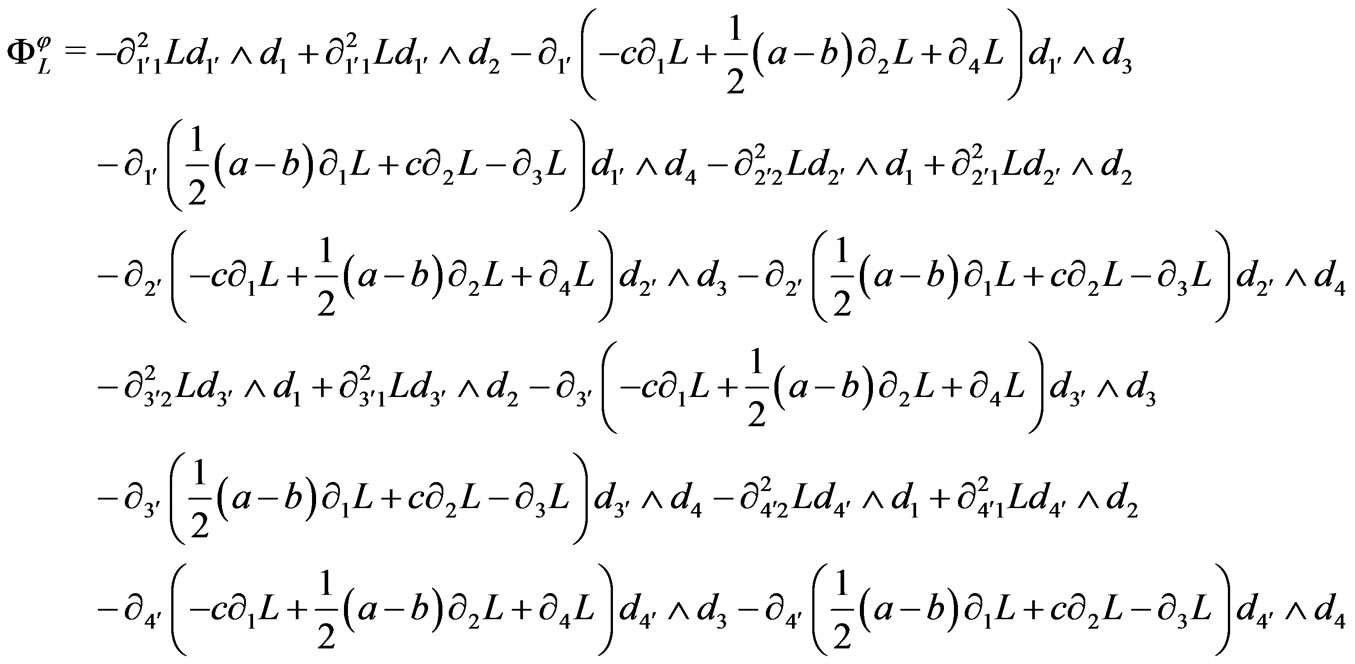(8)

Then the energy function 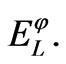is found as follows:

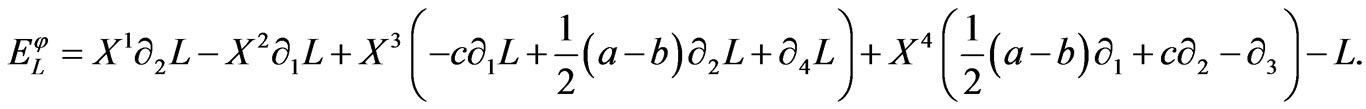(9)

Suppose that a curve

be an integral curve of semispray X. According to (1), using (7) and (9) then we find the following equations:

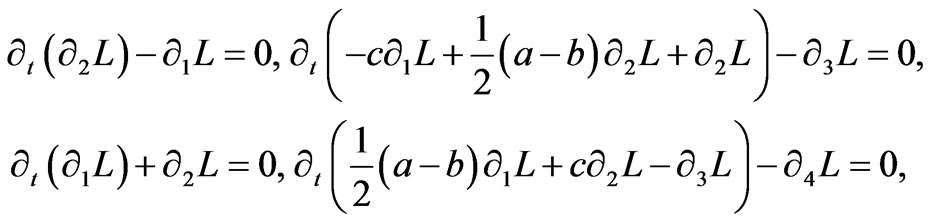(10)

such that the equations calculated in (10) are named complex Euler-Lagrange equations constructed on Walker manifold M₄ if 2-form 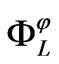is symplectic structure. Thus the triple 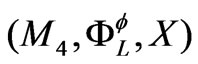is named a complex mechanical system on Walker manifold M₄.

Now we obtain some corollaries about the equations raised in (10) thinking Remark (p. 387) in [14] and Proposition 4 in [8] and Corollary 4 in [15]:

Corollary 1: In (10), if c = 0 and a = b we find the equations as follows:

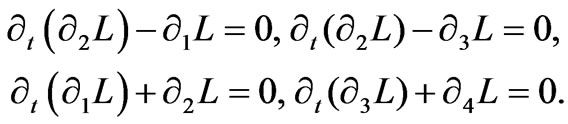(11)

By means of Theorem 2 and Theorem 3 (p. 387 and p. 388) in [14], we can derive the following corollaries:

Corollary 2: If a and b satisfy the following PDEs:

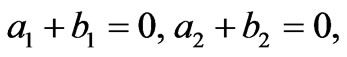
then the equations in (10) are

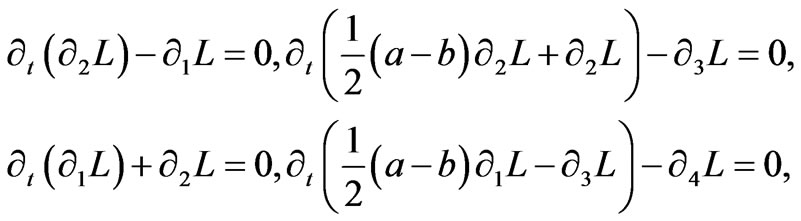(12)

and have a solution.

Corollary 3: If the following PDEs hold:

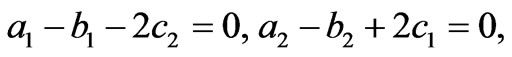
then the equations in (10) have a solution.

4. Hamiltonian Mechanical Systems

This section is devoted to present complex Hamiltonian equations and Hamiltonian mechanical systems for relativistic, quantum and classical mechanics constructed on Walker manifold M₄.

Assume that a Liouville form and a 1-form on Walker manifold M₄ are shown and, respectively

Let us consider

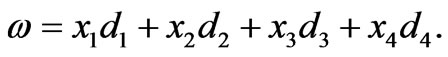(13)

Using (5), we have

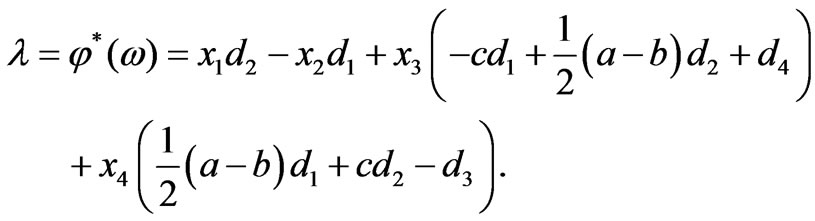(14)

Assume that the vector field X determined by (6) is Hamiltonian vector field associated with Hamiltonian energy function H. Then we find

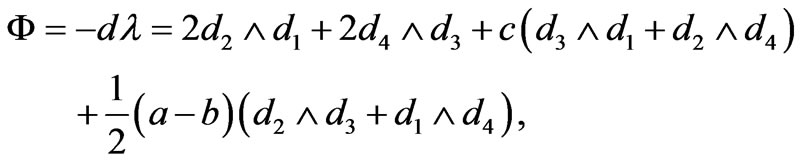(15)

and

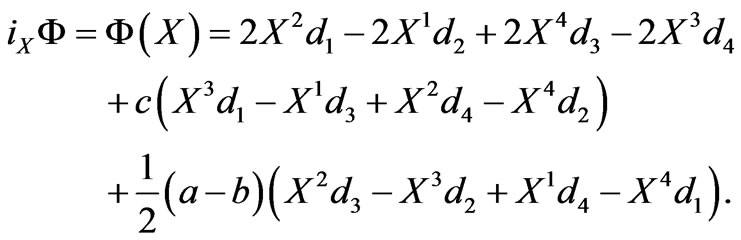(16)

Furthermore, the differential of Hamiltonian energy function is obtained by

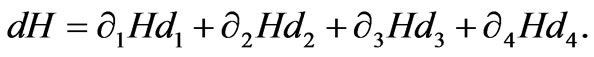(17)

With respect to (2), if (16) and (17) are equaled, the Hamiltonian vector field is found as follows:

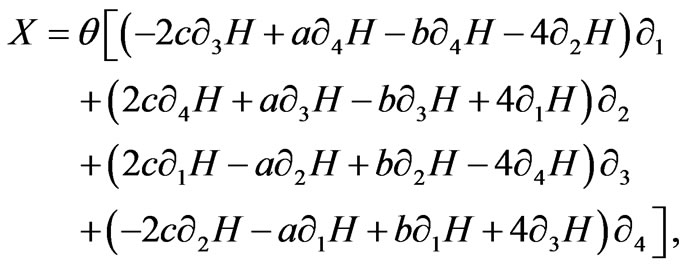(18)

where

Suppose that a curve

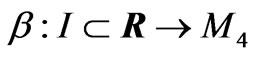
be an integral curve of the Hamiltonian vector field X, i.e.,

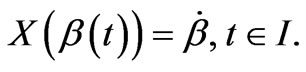(19)

In the local coordinates, taking

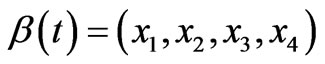
we find

(20)

Using (19), (18), (20), it holds

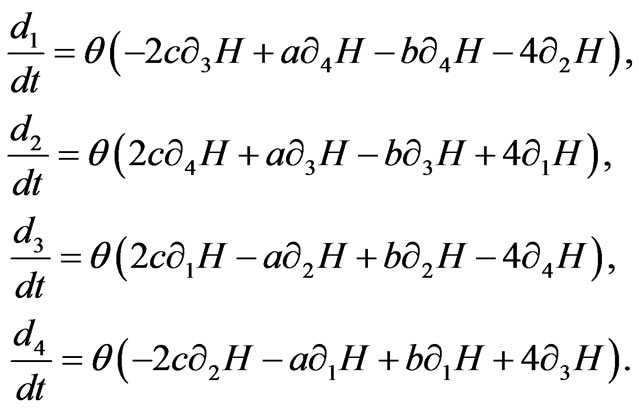(21)

As is known that if Φ is a closed form on Walker manifold M₄, then Φ is also a symplectic structure on Walker manifold M₄ [14]. Hence, the equations introduced in (21) are named complex Hamiltonian equations on Walker manifold M₄ if Φ is a symplectic structure.

Then the triple 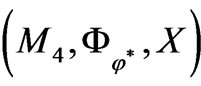is named a complex Hamiltonian mechanical system on Walker manifold M₄.

We obtain the following corollary considering the equations found in (21) using Remark (p. 387) in [14] and Proposition 4 in [8] and Corollary 4 in [15].

Corollary 4: In (21), if c = 0 and a = b we find the equations as follows:

(22)

Taking Theorem 2 and Theorem 3 (p. 387 and p. 388) in [14], we can derive some corollaries as follows:

Corollary 5: If a and b satisfy the following PDEs:

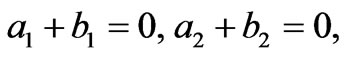
then the equations in (21) are

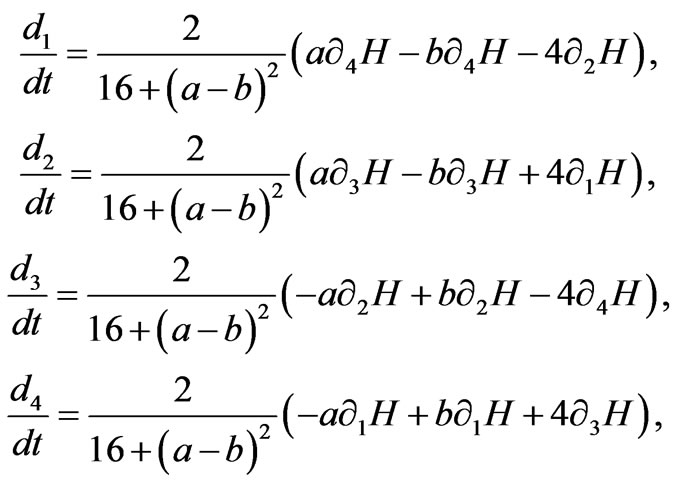(23)

and have a solution.

Corollary 6: If the following PDEs hold:

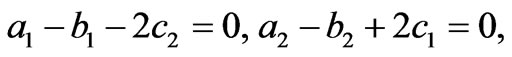
then the equations in (21) have a solution.

5. Paracomplex Lagrangian and Hamiltonian Mechanical Systems

In this section, we produce a paracomplex analogues of Lagrangian and Hamiltonian mechanical systems on a Walker manifold M₄.

Let be a proper almost paracomplex structure on a Walker manifold M₄, which satisfies

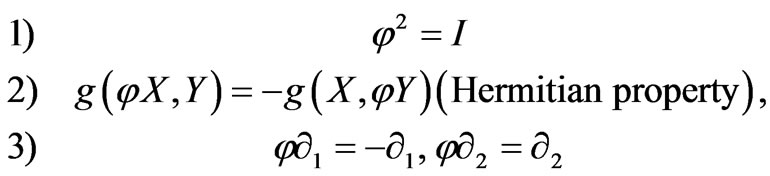
Associated to any Walker metric (3) we consider a proper almost para-Hermitian structure defined by

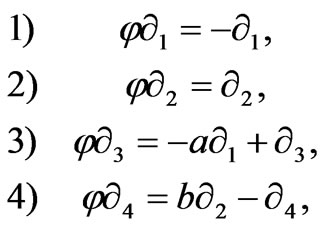(24)

where, i = x₁, x₂, x₃, x₄. denotes the coordinate bases [9].

If we write as 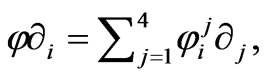then from (24) we can read off the nonzero components 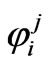as follows:

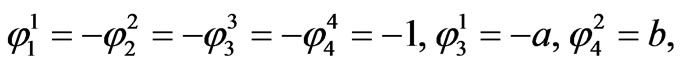
i.e., 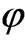has the local components

with respect to the natural frame.

According to the proper almost paracomplex structure, the 2-form 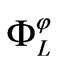is given by as follows:

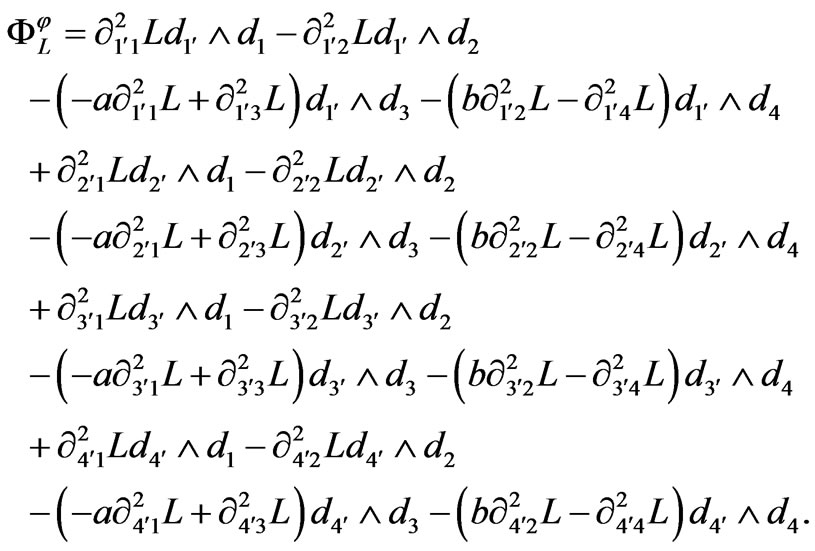
By means of, using similar method in Section 3, we get

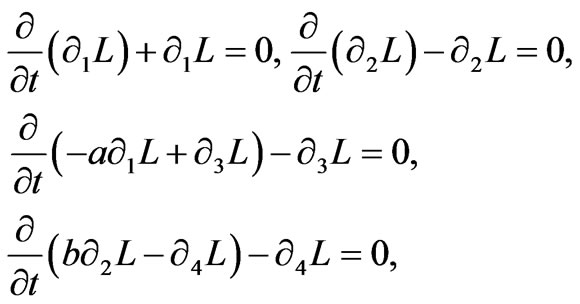(25)

such that the equations calculated in (25) are named a paracomplex Euler-Lagrange equations constructed on the Walker manifold M₄ if the 2-form is symplectic structure. Hence the triple 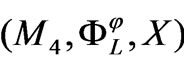is named a paracomplex mechanical system on the Walker manifold M₄.

Now, let us consider the proper almost paracomplex structure: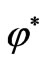

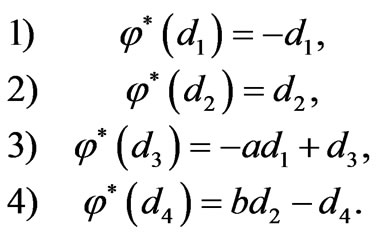
For the proper almost paracomplex structure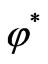, the 2-form 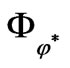is given by

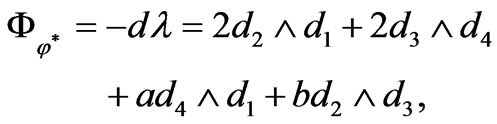(26)

By using similar method in Section 4, by means of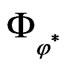, we have

(27)

Hence, the equations introduced in (27) are named a paracomplex Hamiltonian equations on the Walker manifold M₄ if the 2-form is symplectic structure.

Then the triple is named a paracomplex Hamiltonian mechanical system on the Walker manifold M₄.

6. Discussions

From above, complex and paracomplex Lagrangian mechanical systems have intrinsically been described on a Walker manifold M₄: The paths of semispray X on Walker manifold M₄ are the solutions of complex and paracomplex Euler-Lagrange equations raised in (10) and (25).

Also, complex and paracomplex Hamiltonian mechanical systems have intrinsically been described on a Walker manifold M₄. The paths of Hamilton vector field X on the Walker manifold M₄ are the solutions of complex and paracomplex Hamiltonian equations raised in (21) and (27).

One easily see that the complex (paracomplex) EulerLagrange and Hamilton equations introduced in [4,5] are equivalent those in (10) and (21) ((25) and (27)) if a = b = 0.

One can be proved that the here obtained equations are very important to explain the space-time mechanicalphysical problems. Therefore, the found equations are only considered to be a first step to realize how complex (paracomplex) structures on a Walker manifold has been used in solving problems in different physical areas.

For further research, the complex (paracomplex) Lagrangian and Hamiltonian mechanical equations derived here are suggested to deal with problems in electrical, magnetical and gravitational fields of relativistic, quantum and classical mechanics of physics.

REFERENCES