Applied Mathematics
Vol.4 No.7(2013), Article ID:34318,9 pages DOI:10.4236/am.2013.47143
Numerical Solution of Model of Cancer Invasion with Tissue
Department of Mathematics, Iran University of Science and Technology, Tehran, Iran
Email: *farhad_hatami@mathdep.iust.ac.ir
Received May 10, 2013; revised June 10, 2013; accepted June 17, 2013
Keywords: Chemotaxis; Haptotaxis; Model of Cancer Invasion; New Homotopy Perturbation Method
ABSTRACT
Chemotaxis-haptotaxis model of cancer invasion with tissue remodeling is one of the important PDE’s systems in medicine, mathematics and biomathematics. In this paper we find the solution of chemotaxis-haptotaxis model of cancer invasion using the new homotopy perturbation method (NHPM). Then by comparing some estimated numerical result with simulation laboratory result, it shows that NHPM is an efficient and exact way for solving cancer PDE’s system.
Keywords: Chemotaxis; Haptotaxis; Model of Cancer Invasion; New Homotopy Perturbation Method
1. Introduction
Cancer invasion model is a so complex process which includes many biological procedures. Actually, different models in Mathematics were improved for many kind of cancer disease and also so many scientists tried to give more proper and applicable models (see [1], as an instance).
Cancer is connected with degradation of the extracellular matrix (ECM) that is degraded with the matrix degradation enzymes (MDEs) which are concealed by colony of tumor cells. The degradation produces spatial gradients which aim movement of invasive cells through a procedure named chemotaxis (cellular locomotion aimed to response to a concentration gradient of the diffusible MDE) or through a procedure which is called haptotaxis (cellular locomotion aimed to response to an association gradient of the non-diffusible adhesive molecules within extracellular matrix). Chaplain et al. [2,3] introduced a system of partial differential equations of cancer invasion with tissue. As long as this introduction, other researchers proved uniqueness and existence of solutions associated to this PDE model [4-8].
Chemotaxis-haptotaxis model of cancer invasion with tissue remodeling [6] like other systems of PDEs are often too complicated to be solved exactly and even if an exact solution is obtained, the required calculations may be too complicated. Very recently, many methods have been presented, such as the Adomian decomposition method [9,10], the variational iteration method [11,12] and the differential transform method [13,14].
The homotopy perturbation method (HPM) was proposed by Ji-Huan He [15]. Convergence of the HPM for PDEs is given in [16]. In this method, the solution is considered as the summation of an infinite series, which usually converges rapidly to the exact solution. New homotopy perturbation method (NHPM) is a new modification of HPM which have been used for solving system of PDEs, Efficiency and exactness of this method are more in comparison with HPM (see [17]).
This paper is arranged as follows. Section 2 describes the chemotaxis-haptotaxis model of cancer invasion of tissue. In Section 3, the new modification of HPM which called NHPM is presented. In Section 4 model is solved by NHPM. In Section 5 computed solution by NHPM is compared with simulations results.
2. Mathematical Model of Cancer Invasion
In this section, we recall the setting of [3,18,19]. Cancer invasion model consists of the 3 variables; the matrix degrading enzyme concentration (MDE concentration)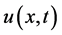 , the extracellular matrix density (ECM density)
, the extracellular matrix density (ECM density) , and the cancer cell density
, and the cancer cell density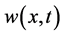 . In this paper, we will investigate the results in case that these 2 characteristic migrating procedures operate synchronously.
. In this paper, we will investigate the results in case that these 2 characteristic migrating procedures operate synchronously.
We assume following boundary conditions presented by the equations from [3]
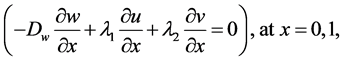 and
and 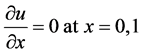
and we consider following the initial conditions
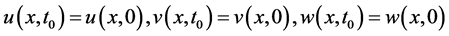 .
.
The equations describing the dynamics of each variable as follows (according to [3]):
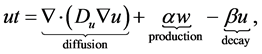 (1.1)
(1.1)
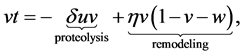 (1.2)
(1.2)
 (1.3)
(1.3)
where 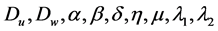 are assumed to be positive constants.
are assumed to be positive constants.
Diffusion-Production-Decay: Now we suppose dispersal cell density is altered. Then let 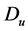 as the cell random motility coefficient, which classify how cells scatter from high-density cells to the low-density ones. In (1.1), the concentration of MDE is affected by diffusion parameter, decay and production.
as the cell random motility coefficient, which classify how cells scatter from high-density cells to the low-density ones. In (1.1), the concentration of MDE is affected by diffusion parameter, decay and production.
Proteolysis: Spread of a cancer disease relay on occupies and metastasizes (for detailed information see [20- 22]).
Chemotaxis: Chemotaxis is movement of microorganisms and cells in response and to a chemical sign and in the enclosing location in tissue [23]. Chemotaxis appears as a key step in a number of biological procedures in body, from fertilization to fight against infectious diseases by immune system. The main studies on the chemotaxis deals with these inquiries that how microorganisms move, when they respond to the chemical signs, and also what can cut off these procedures. During the chemotaxis process, single cells, unicellular organisms, and little multicellular organisms respond to chemicals signals by moving further away from them or closer to them. Single cells, unicellular organisms and multicellular organisms have receptors which are sensitive to specific chemicals of interest so they can respond and react to them, using a variety of approaches for movement.
Chemoattractants are chemicals that prefer to increase the desire to move towards a given chemical origin, while chemorepellants encourage organisms and microorganisms or cells to move in the converse and opposite direction.
Now we give an example to obtain application of chemotaxis process. This process could be both beneficial (in life phenomenon) and destructive (cause of diseases) for body. During the fertilization, chemotaxis is the main step that sexual reproduction depends on, to permit migration of sperms toward an egg, following chemoattractants which produced through the egg. Therefore chemotaxis can complete fertilization.
Chemotaxis could be interrupted by the chemical signals. Confusion and disorientation of cells is the reasons to make mistakes. Another factor to interrupt this movement is limitation by environmental factors which can lead to the errors in navigation; moving organisms toward the toxins and away from sources of nutrition. In a nerve injury moving the new growing cells (during the replacement procedure with the damaged cells) toward a wrong direction may be lead to create a cancer tissue. Also there is a considerable motivation for the researchers in all over the world to learn more about the chemotaxis and correspondence procedures, as this process is very important both in treating injuries and harsh diseases as well as addressing barrenness [see 23].
Haptotaxis: Cell haptotaxis describes cell migration toward or along a gradient of chemoattractants or adhesion sites in the extracellular matrix [24,25].
Proliferation: This rate depends on the kind of cancer disease, age and other biological parameters in patients (see complete details about proliferation in [26,27]).
3. The Basic Idea of NHPM
The general form of a system of PDEs can be considered as the following:
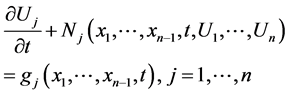 (1.4)
(1.4)
Coresspondence with the following initial conditions:
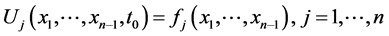
where Uj is the solution of the jth equation, 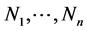 are non-linear operators, which usually depend on the functions Uj and their partial derivatives, and
are non-linear operators, which usually depend on the functions Uj and their partial derivatives, and 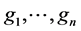 are inhomogeneous terms.
are inhomogeneous terms.
For solving system (1.4) we follow the steps which are quoted from [17], by using NHPM, we construct the following homotopies:

or
 (1.5)
(1.5)
where 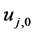 is the initial condition of the jth equation in PDEs system and p is a real number (usually called “embedding parameter”) in the close interval
is the initial condition of the jth equation in PDEs system and p is a real number (usually called “embedding parameter”) in the close interval .
.
By applying the inverse operator,  on the both sides of Equation (1.5), we obtain
on the both sides of Equation (1.5), we obtain
 (1.6)
(1.6)
such that
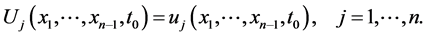
Let us present the solution of the system (1.6) as the following:
 (1.7)
(1.7)
where 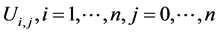 are functions which should be determined. Suppose that the initial approximations of the solutions of (1.4) are in the following form:
are functions which should be determined. Suppose that the initial approximations of the solutions of (1.4) are in the following form:
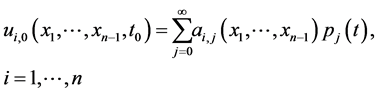 (1.8)
(1.8)
where 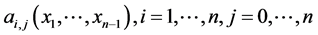 are unknown coefficients and
are unknown coefficients and  are specific functions.
are specific functions.
Substituting (1.7) and (1.8) into (1.6) and equating the coefficients of p with the same powers leads to
 (1.9)
(1.9)
Now if we solve these equations in such a way that , then Equations (1.9) yield
, then Equations (1.9) yield
 .
.
Therefore the exact solution may be obtained as the following:

It is worth mentioning that if , and
, and  , are analytic around
, are analytic around  , then their Taylor series can be defined as
, then their Taylor series can be defined as


which can be used in (1.9), 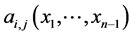 ,
, 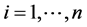 ,
, 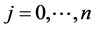 , are unknown coefficients which must be computed, and
, are unknown coefficients which must be computed, and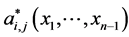 ,
,  ,
,  , are known ones.
, are known ones.
4. Solving System by Using NHPM
In this section we are going to solve this complicated PDEs model numerically and by using the so-called modification of the Homotopy Perturbation Method that named New Homotopy perturbation Method. We just calculate two order of the He’s polynomials but you will see how is the exactness of this way and be motivate and interested to use this numerical way in your models and systems.
By definitions of gradient  and laplacian
and laplacian 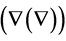 Equations (1.1)-(1.3) can be rewritten as follows:
Equations (1.1)-(1.3) can be rewritten as follows:

For solving this system by using NHPM, we consider the following homotopy (under this assumption which 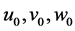 are solutions):
are solutions):
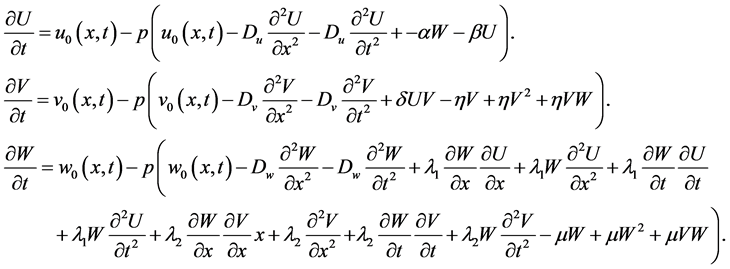 (1.10)
(1.10)
Applying the inverse operator,  , on the both sides of the system (1.10) and assuming solutions of system like presented form in (1.7) leads to
, on the both sides of the system (1.10) and assuming solutions of system like presented form in (1.7) leads to
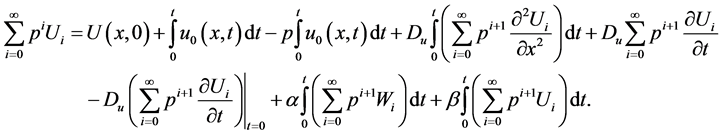

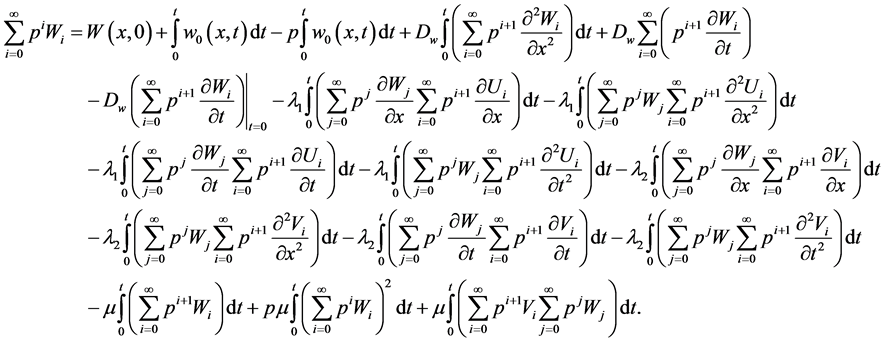
Substituting Equation (1.7) into the above equations, collecting the terms with the same powers of  and equating each coefficient of
and equating each coefficient of  to zero, we obtain
to zero, we obtain
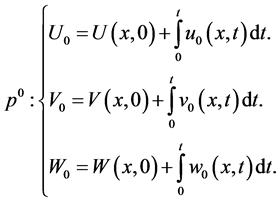 (1.11)
(1.11)

According to the previous section, assume
 (1.12)
(1.12)
By substituting (1.12) into (1.11), 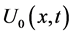 ,
, 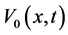 ,
,  ,
,  ,
, 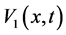 ,
,  ,
, 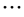 can be calculated easily. Now if we set the Taylor series of
can be calculated easily. Now if we set the Taylor series of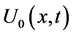 ,
, 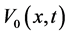 ,
,  ,
,  ,
, 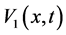 ,
,  at t = 0 equal to zero, then the coefficients
at t = 0 equal to zero, then the coefficients ,
, 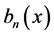 ,
, 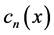 ,
,  are determined as follows (at the first step for
are determined as follows (at the first step for 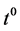 we have
we have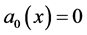 ,
, ).
).
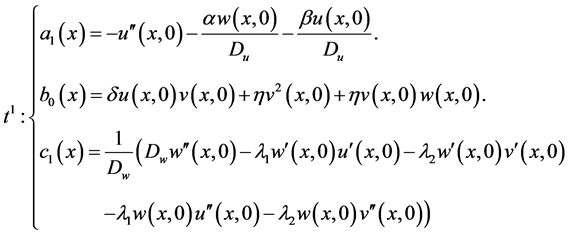

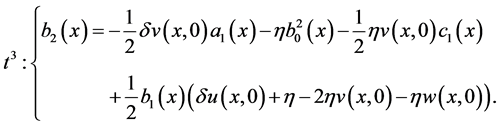
Finally it is done and we reached to the finall solutions. Solutions preferably are written in their completed form and without any simplification for using and examinig of readers. Note that you can replace your constant parameters and initial conditions without any restrictions, because you can use you can use initial conditions, v, u, w in their function forms depending on x and their derivations to x.
Now
 ,
,
 ,
,

and therefore solutions can be expressed as follows:

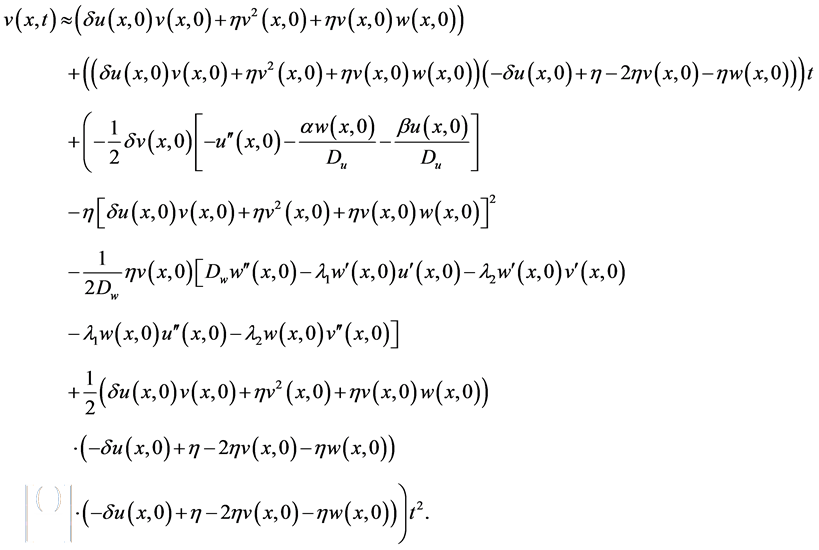
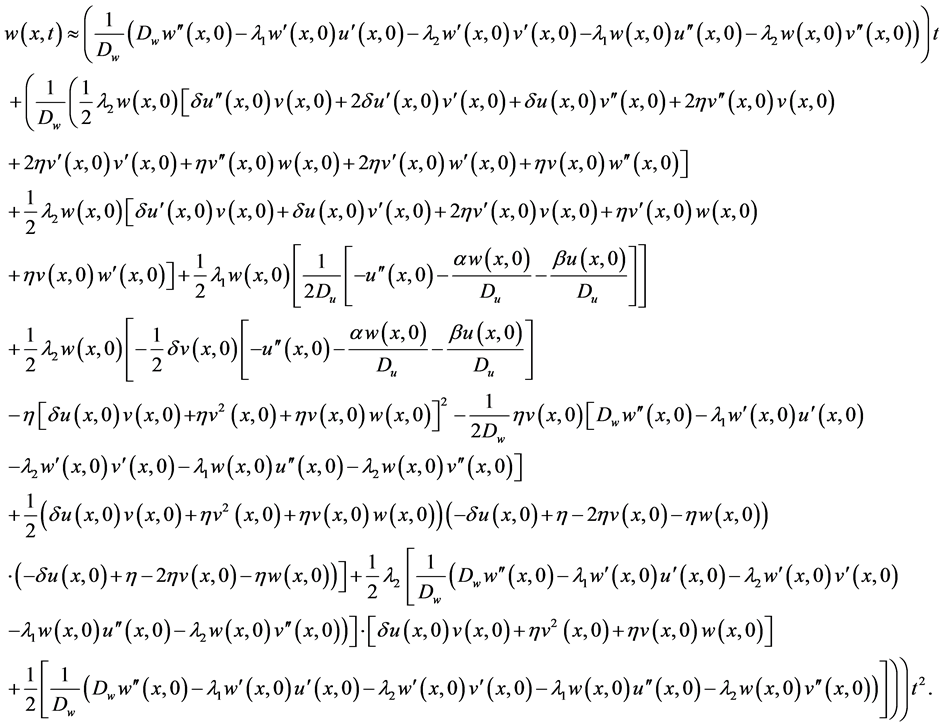
5. Comparing with Simulation’s Results
In this section ,
,  ,
,  which are obtained by new homotopy perturbation method (NHPM), are compared with reality numerical simulation. Aim of this section is to show the exactness of the presented “New Homotopy Perturbation Method (NHPM)” by comparing with computer results and laboratories results.
which are obtained by new homotopy perturbation method (NHPM), are compared with reality numerical simulation. Aim of this section is to show the exactness of the presented “New Homotopy Perturbation Method (NHPM)” by comparing with computer results and laboratories results.
All of our requiremetns for reaching to this purpose is initial conditions and positive constants. Now consider the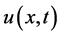 ,
, 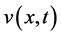 ,
, 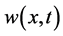 which was calculated in the past section with the following initial conditions according to Lolas and Chaplain’s results (see [3])
which was calculated in the past section with the following initial conditions according to Lolas and Chaplain’s results (see [3])
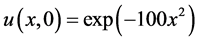
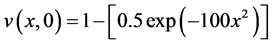
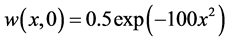
additionally, consider every t equal to 3 hours and numerical result of positive parameters according to [3] as follows
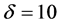
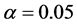
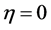
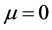


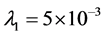

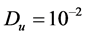
At this stage, by using the Maple software (version 15) and plotting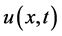 ,
, 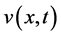 ,
,  which are computed by NHPM we obtain
which are computed by NHPM we obtain
Figure 1 shows difference between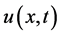 ,
, 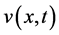 ,
, 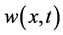 which are estimated and computed by NHPM and
which are estimated and computed by NHPM and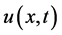 ,
,  ,
,  which are obtained by laboratory’s results from [3], is very close. Graph of the NHPM results is almost adjacent to laboratory’s results and this can demonstrate the exactness of the NHPM.
which are obtained by laboratory’s results from [3], is very close. Graph of the NHPM results is almost adjacent to laboratory’s results and this can demonstrate the exactness of the NHPM.
As you saw in past section, we calculated and estimated our solutions just by by two steps and orders (with very long term and complicated calculations) in the NHPM, but the figures show it is sufficient for our estimation. While by the Homotopy Perturbation Method (HPM) and Adomian Decomposition Method (ADM) we had to collapse finall series to a well known or calculate another orthers and steps for a exact solution, the New Homotopy Perturbation Method (NHPM) reached to the exact solution just by two steps of our calculating.
In Figure 2, 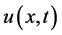 ,
,  ,
, 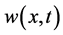 (which are computed by NHPM) are plotted in 3D scheme using the Maple software. By observing Figure 1 and comparing with Figure 2 (that is a real capture from a cancer cell) it is seen NHPM results approach to the laboratory and
(which are computed by NHPM) are plotted in 3D scheme using the Maple software. By observing Figure 1 and comparing with Figure 2 (that is a real capture from a cancer cell) it is seen NHPM results approach to the laboratory and

Figure 1. 2D figures in above: (Horizonal axis: x (cm)) Comparing laboratory and simulation’s results ([3]) (doted line) with results were obtained by NHPM (solid line). It shows MDE concentration u(x, t) (Orange line, (a)), ECM density v(x, t) (red line, (b)) and cancer cell density w(x, t) (blue line, (c)) in t = 100 (300 hours or about 12 days). The difference between simulation results and NHPM results are very small.
u(x, t) v(x, t) w(x, t)
(a) (b) (c)


Figure 2. 3D graphics of results were obtained by NHPM. MDE concentration u(x, t) (orange shape, (a)) and ECM density v(x, t) (red shape, (b)) in t = 100 (300 hours or about 12 days). More about process of the u and v in Figure 2: Plots of the spatiotemporal evolution of the degraded matrix density. A wave of chemoattractants and growth factors arises from the degraded extracellular matrix. This leads cells to proliferate and migrate which, in turn, continues the stimulation of enzyme production and the corresponding degradation of the ECM. As a result, a migration feedback loop is established.
u(x, t) v(x, t)
(a) (b)
simulation’s results at  (12 days).
(12 days).
6. Conclusion
New homotopy perturbation method (NHPM) is applied to the numerical solution for solving chemotaxis-haptotaxis model of cancer invasion of tissue (a complicated nonlinear PDEs system). As it was seen, differences between simulation results and NHPM results are very small. Thus the present method is very effective and convenient. Our suggestion is to use this numerical way to solve other PDEs system for example in biology.
REFERENCES
- N. Bellomo, N. K. Li and P. K. Maini, “On the Foundations of Cancer Modelling: Selected Topics, Speculations, and Perspectives,” Mathematical Models and Methods in Applied Sciences, Vol. 18, No. 4, 2008, pp. 593-646. doi:10.1142/S0218202508002796
- M. A. J. Chaplain and A. R. A. Anderson, “Mathematical modelling of Tissue Invasion, Cancer Modelling and Simulation,” Chapman and Hall/CRT, 2003, pp. 267-297.
- M. A. J. Chaplain and G. Lolas, “Mathematical Modelling of Cancer Invasion of Tissue: Dynamic Heterogeneity,” Networks and Heterogeneous Media, Vol. 1, 2006, pp. 399-439. doi:10.3934/nhm.2006.1.399
- Y. Tao, “Global Existence of Classical Solutions to a Combined Chemotaxis Haptotaxis Model with Logistic Source,” Journal of Mathematical Analysis and Applications, Vol. 354, No. 1, 2009, pp. 60-69. doi:10.1016/j.jmaa.2008.12.039
- C. Walker and G. F. Webb, “Global Existence of Classical Solutions for a Haptotaxis Model,” SIAM Journal on Mathematical Analysis, Vol. 38, No. 5, 2007, pp. 1694- 1713. doi:10.1137/060655122
- Y. Tao, “Global Existence for a Haptotaxis Model of Cancer Invasion with Tissue Remodeling,” Nonlinear Analysis: Real World Applications, Vol. 12, No. 1, 2011, pp. 418-435. doi:10.1016/j.nonrwa.2010.06.027
- Y. Tao and M. Wang, “Global Solution for a Chemotactic-Haptotactic Model of Cancer Invasion,” Nonlinearity, Vol. 21, No. 10, 2008, pp. 2221-2238. doi:10.1088/0951-7715/21/10/002
- Y. Tao and M. Wang, “A Combined Chemotaxis-Haptotaxis System: The Role of Logistic Source,” SIAM Journal on Mathematical Analysis, Vol. 41, No. 4, 2009, pp. 1533-1558. doi:10.1137/090751542
- Y. Cherruault and G. Adomian, “Decomposition Methods: A New Proof of Convergence,” Mathematical and Computer Modelling, Vol. 18, No. 12, 1993, pp. 103-106. doi:10.1016/0895-7177(93)90233-O
- A. M. Wazwaz, “The Decomposition Method Applied to Systems of Partial Differential Equations and to the Reaction Diffusion Brusselator Model,” Applied Mathematics and Computation, Vol. 110, No. 2-3, 2000, pp. 251-264. doi:10.1016/S0096-3003(99)00131-9
- J. H. He, “Variational Iteration Method a Kind of NonLinear Analytical Technique: Some Examples,” International Journal of Non-Linear Mechanics, Vol. 34, No. 4, 1999, pp. 699-708. doi:10.1016/S0020-7462(98)00048-1
- S. Momani and S. Abuasad, “Application of He Variational Iteration Method to Helmholtz Equation,” Chaos, Solitons and Fractals, Vol. 27, No. 5, 2005, pp. 1119- 1123. doi:10.1016/j.chaos.2005.04.113
- C. K. Chen, “Solving Partial Differential Equations by Two Dimensional Differential Transform,” Applied Mathematics and Computation, Vol. 106, No. 2-3, 1999, pp. 171-179. doi:10.1016/S0096-3003(98)10115-7
- F. Ayaz, “On the Two-Dimensional Differential Transform Method,” Applied Mathematics and Computation, Vol. 143, No. 2-3, 2003, pp. 361-374. doi:10.1016/S0096-3003(02)00368-5
- J. H. He, “Homotopy Perturbation Technique,” Computer Methods in Applied Mechanics and Engineering, Vol. 178, No. 3-4, 1999, pp. 257-262. doi:10.1016/S0045-7825(99)00018-3
- J. Biazar and H. Ghazvini, “Convergence of the Homotopy Perturbation Method for Partial Differential Equations,” Nonlinear Analysis: Real World Applications, Vol. 10, No. 5, 2009, pp. 2633-2640. doi:10.1016/j.nonrwa.2008.07.002
- J. Biazar and M. Eslami, “A New Homotopy Perturbation Method for Solving Systems of Partial Differential Equations,” Computers and Mathematics with Applications, Vol. 62, No. 1, 2011, pp. 225-234. doi:10.1016/j.camwa.2011.04.070
- K. Baghaei, M. B. Ghaemi and M. Hesaaraki, “Global Existence of Classical Solutions to a Cancer Invasion Model,” Applied Mathematics, Vol. 3, No. 4, 2012, pp. 382-388. doi:10.4236/am.2012.34059
- Y. Tao and G. Zhu, “Global Solution to a Model of Tumor Invasion,” Applied Mathematical Sciences, Vol. 1, No. 48, 2007, pp. 2385-2398.
- P. A. Andreasen, L. Kjoller, L. Christensen and M. J. Duffy, “The Urokinase-Type Plasminogen Activator System in Cancer Metastasis: A Review,” International Journal of Cancer, Vol. 72, No. 1, 1997, pp. 1-22. doi:10.1002/(SICI)1097-0215(19970703)72:1<1::AID-IJC1>3.0.CO;2-Z
- P. A. Andreasen, R. Egelund and H. H. Petersen, “The Plasminogen Activation System in Tumor Growth, Invasion, and Metastasis,” Cellular and Molecular Life Sciences, Vol. 57, No. 1, 2000, pp. 25-40. doi:10.1007/s000180050497
- F. Blasi, J.-D. Vassalli and K. Dan, “Urokinase-Type Plasminogen Activator: Proenzyme, Receptor, and Inhibitors,” Journal of Cell Biology, Vol. 104, No. 4, 1987, pp. 801-804. doi:10.1083/jcb.104.4.801
- J. M. Lackie and P. C. Wilkinson, Eds., “Biology of the Chemotactic Response,” Cambridge University Press, Cambridge, 1981.
- S. B. Carter, “Haptotaxis and the Mechanism of Cell Motility,” Nature, Vol. 213, No. 5073, 1967, pp. 256-260. doi:10.1038/213256a0
- A. S. G. Curtis, “The Measurement of Cell Adhesiveness by an Absolute Method,” Journal of Embryology and Experimental Morphology, Vol. 22, 1969, pp. 305-325.
- A. R. A. Anderson, M. A. J. Chaplain, E. L. Newman, R. J. C. Steele and A. M. Thompson, “Mathematical Modelling of Tumour Invasion and Metastasis,” Journal of Theoretical Medicine, Vol. 2, No. 2, 2000, pp. 129-154. doi:10.1080/10273660008833042
- H. M. Byrne, M. A. J. Chaplain, G. J. Pettet and D. L. S. McElwain, “A Mathematical Model of Trophoblast Invasion,” Journal of Theoretical Medicine, Vol. 1, No. 4, 1998, pp. 275-286. doi:10.1080/10273669908833026
NOTES
*Corresponding author.

