Journal of Applied Mathematics and Physics
Vol.07 No.01(2019), Article ID:89944,15 pages
10.4236/jamp.2019.71011
On the Equivalence of Implicit Kirk-Type Fixed Point Iteration Schemes for a General Class of Maps
Alfred Olufemi Bosede1, Hudson Akewe2, Omolara Fatimah Bakre3, Ashiribo Senapon Wusu1
1Department of Mathematics, Lagos State University, Ojo, Nigeria
2Department of Mathematics, University of Lagos, Akoka, Nigeria
3Department of Mathematics & Statistics, Federal College of Education (Technical), Akoka, Nigeria
Copyright © 2019 by author(s) and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: December 16, 2018; Accepted: January 14, 2019; Published: January 17, 2019
ABSTRACT
In this paper, a modified implicit Kirk-multistep iteration scheme and a strong convergence result for a general class of maps in a normed linear space was established. It was also shown that the convergence of this iteration scheme is equivalent to the convergency of some other implicit Kirk-type iteration (implicit Kirk-Noor, implicit Kirk-Ishikawa and implicit Kirk-Mann iterations) for the same class of maps. Some numerical examples were considered to show that the equivalence of convergence results to the fixed point is true. The results unify most equivalence results in literature.
Keywords:
Implicit Kirk-Multistep, Implicit Kirk-Mann Iterations, Strong Convergence, Equivalence, General Class of Maps

1. Introduction
In 1971, Kirk introduced the Kirk iterative scheme as follows: Let be a normed linear space and D a non-empty, convex, closed subset of E and be a selfmap of D, let , the sequence is defined by
(1)
Various authors have written inspiring papers on Kirk-type iterative schemes. Worthy to mention are the following: the explicit Kirk-Mann, Olatinwo [1] , explicit Kirk-Ishikawa, Olatinwo [1] , Kirk-Noor, Chugh and Kumar [2] and Kirk-multistep, Akewe, Okeke and Olayiwola [3] iterative schemes.
In 2014, Akewe, Okeke and Olayiwola [3] proposed an explicit Kirk-multistep iterative schemes and proved strong convergence and stability results for contractive-like operators in a normed linear space, the researchers also gave useful numerical examples to back up their schemes. The authors in Chugh, Malik and Kumar [4] made the following statements in their introduction: “Implicit iterations have an advantage over explicit iterations for nonlinear problems as they provide better approximation of fixed points and are widely used in many applications when explicit iterations are inefficient. Approximation of fixed points in computer oriented programs by using implicit iterations can reduce the computational cost of the fixed point problems”. They considered a new implicit iteration and study its strong convergence, stability, and data dependence and also proved through numerical examples that newly introduced iteration has better convergence rate than well known implicit Mann iteration as well as implicit Ishikawa iteration and that implicit iterations converge faster as compared to corresponding explicit iterations. However, it was observed that little work has been done on equivalence of implicit scheme.
The main aim of this work is in three folds: firstly, to develop a modified implicit Kirk-multistep scheme and prove strong convergence results for a general class of mapping introduced by Bosede and Rhoades [5] . Secondly, to show that the convergence of the implicit Kirk-multistep iteration scheme is equivalent to the convergency of implicit Kirk-Noor, implicit Kirk-Ishikawa and implicit Kirk-Mann iterations for the same class of mapping under consideration.
Let be a normed linear space and D a non-empty, convex, closed subset of E and be a selfmap of D, let . Then, the sequence defined by
(2)
where , for each j, , , , , for each j, for each j and , are fixed integers (for each j). (2) is called implicit Kirk-multistep iterations.
Equation (2) serves as a general formula for obtaining other implicit Kirk-type iterations. Infact, if in (2), we obtain a three step (implicit Kirk-Noor) iteration as follows:
(3)
where , , , , , , , and and are fixed integers.
If in (2), we obtain a two step (implicit Kirk-Ishikawa) iteration as follows:
(4)
where , , , , , and and are fixed integers.
Finally, if and in (2), we obtain a one step (implicit Kirk-Mann) iteration as follows:
(5)
where , , and is a fixed integer.
Equations (3)-(5) will be rewritten in the following forms to help us prove our equivalence result:
Let be a normed linear space and D a non-empty, convex, closed subset of E and be a selfmap of D, let . Then, the implicit Kirk-Noor scheme is a sequence defined by
(6)
where , , , , , , , and and are fixed integers.
Also, for , the two step (implicit Kirk-Ishikawa) iteration scheme is a sequence defined as follows:
(7)
where , , , , , and and are fixed integers.
Finally, for , the implicit Kirk-Mann iteration scheme is a sequence defined by:
(8)
where , , and is a fixed integer. We shall now consider some of the contractive mappings useful in proving our main results.
Let E be a normed linear space and D a non-empty, convex, closed subset of E and be a selfmap of D. There exists a real number and all such that
(9)
Zamfirescu [6] , discussed mappings T satisfying the following contractive condition:
(10)
where . Inequality (10) becomes (9) if x is a fixed point of T.
Osilike [7] proved several stability results which are generalizations and extensions of most of the results of Rhoades [8] using the following contractive definition: for each , there exist and such that
(11)
In 2003, Imoru and Olatinwo [9] proved some stability results using the following general contractive definition: for each , there exists and a monotone increasing function with such that
(12)
In 2010, Bosede and Rhoades [5] , made an assumption implied by (9) and one which attempted to put an end to all generalizations of the form (12). That is if (is a fixed point) then (12) becomes inequality (9).
In 2014, Chidume and Olaleru [10] gave several examples to show that the class of mappings satisfying (9) is more general than that of (10), (11) and (12) provided the fixed point exists.
We shall need the following lemma in proving our result.
Lemma 1.2 [11] : Let be a real number satisfying and a sequence of positive numbers such that , then for any sequence of positive numbers satisfying
(13)
we have .
Lemma 1.3 [12] : Let and be nonnegative real sequences satisfying the following inequality , where , for all , and . Then
2. Main Result
Theorem 2.1. Let be a normed linear space, D a non-empty, convex, closed subset of E and , a self map satisfying the inequality:
(14)
where and . For , let be the implicit Kirk-multistep iteration scheme defined by (2) with . Then
i) the fixed point p of T defined by (14) is unique;
ii) the implicit Kirk-multistep iteration scheme converges strongly to the unique fixed point p of T.
Proof:
i) The first thing is to establish that the mapping T satisfying the contractive condition (14) has a unique fixed point.
Suppose there exist , and that , with , then,
(15)
Since , then and . Since norm is nonnegative we have that . That is, (say). Thus, T has a unique fixed point p.
ii) Next, we prove that (2) converges strongly to p. In veiw of (2) and (14),
(16)
Also, using (2) and (14), we have:
(17)
Again, using (2) and (14), we have:
(18)
Continuing the process using (2) and (14), we have
(19)
Finally, using (2) and (14) for , we have:
(20)
Substituting (20) in (19), (19) in (18), (18) in (17) and (17) in (16), we obtain:
(21)
Note that
(22)
hence
Let , then
(23)
That is,
(24)
Therefore,
(25)
Hence, using Lemma 1.2 in (25), then This ends the proof.
Theorem 2.1 leads to the following corollary:
Corollary 2.2. Let be a normed linear space, D a non-empty, convex, closed subset of E and , with , such that:
(26)
where . For , let be the implicit Kirk-Noor, implicit Kirk-Ishikawa and implicit Kirk-Mann iteration scheme respectively defined by (6), (7) and (8) with , , . Then
i) T defined by (26) has a unique fixed point p;
ii) (6) converges strongly to the unique fixed point p of T;
iii) (7) converges strongly to the unique fixed point p of T;
iv) (8) converges strongly to the unique fixed point p of T.
Theorem 2.3. Let be a normed linear space, D a non-empty, convex, closed subset of E and an operator satisfying
(27)
where and . If , then the following are equivalent: the
i) implicit Kirk-Mann iterative scheme (8) converges strongly to p;
ii) implicit Kirk-multistep iterative scheme (2) converges strongly to p.
Proof:
We prove that (i) Þ (ii).
Assume , then using (8), (2) and (27), we have
(28)
Using condition (27) in (28), we have
(29)
From (29),
(30)
From (30),
(31)
But from (31),
(32)
Applying condition (27) on (31), we get
(33)
Using (33) in (31), we have
(34)
Similarly,
(35)
Also
(36)
Continuing (k − 2) times, we have
(37)
Moving a step more, we have
(38)
Substituting (35) into (34), (34) into (33), (33) into (32) and (32) into (31) respectively, we obtain
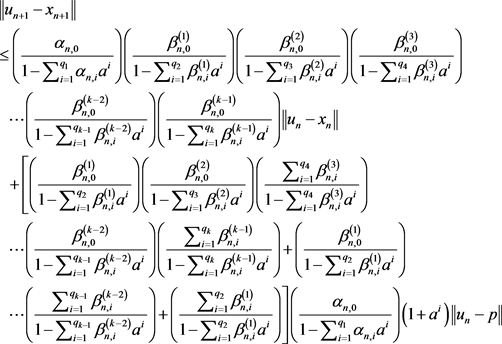 (39)
(39)
Recall that
(40)
Let , then
(41)
Using (36), (37) in (38), we have
(42)
Let and
(43)
Replacing (40) in (39), we have
(44)
By Lemma 1.3 in (41), it follows that
(45)
Since by the assumption, ,
then as
Hence .
Next is to show that (ii) implies (i).
Assume, , then using (2), (8) and (27), we have
(46)
(47)
By simplifying (42), we obtain
(48)
But,
(49)
Substituting (44) in (43), we have
(50)
Similarly,
(51)
Also,
(52)
Continuing the process upto (k − 2), we have
(53)
For (k − 1), we get
(54)
Substituting accordingly from (41) to (48), we get
(55)
(50) can be written as:
(56)
Let
Therefore,
(57)
It follows from Lemma 1.3 that:
Since by assumption, Then, .
This implies that .
Since (i) → (ii) and (ii) → (i), it shows that the convergence of implicit Kirk-Mann iterative scheme (8) is equivalent to the convergence of implicit Kirk-multistep iterative scheme (2) when applied to the general class of map (14). This ends the proof.
Theorem 2.3 leads to the following Corollaries:
Corollary 2.4. Let be a normed linear space, D a non-empty, convex, closed subset of E and , with , satisfying
(58)
where . If , then the following are equivalent: the
a) (i) implicit Kirk-Mann iterative scheme (8) converges strongly to p;
(ii) implicit Kirk-Ishikawa iterative scheme (7) converges strongly to p.
b) (i) implicit Kirk-Mann iterative scheme (8) converges strongly to p;
(ii) implicit Kirk-Noor iterative scheme (6) converges strongly to p.
Proof. The proof of Corollary 2.4 is similar to that of Theorem 2.3.This ends the proof.
Corollary 2.5. Let
be a normed linear space, D a non-empty, convex, closed subset of E and 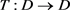 an operator satisfying
an operator satisfying
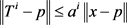 (59)
(59)
where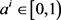 . If
. If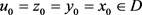 , then the following are equivalent:
, then the following are equivalent:
i) implicit Kirk-Mann iterative scheme 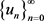 (8) converges strongly to p;
(8) converges strongly to p;
ii) implicit Kirk-Ishikawa iterative scheme 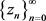 (7) converges strongly to p;
(7) converges strongly to p;
iii) implicit Kirk-Noor iterative scheme 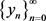 (6) converges strongly to p;
(6) converges strongly to p;
iv) implicit Kirk-multistep iterative scheme 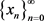 (2) converges strongly to p.
(2) converges strongly to p.
3. Numerical Examples
In this section, we use some examples to demonstrate the equivalence of convergence between implicit Kirk-multistep (IKMST) iterative scheme (2) and other implicit Kirk-type [implicit Kirk-Noor (IKN)(6), implicit Kirk-Ishikawa (IKI)(7) and implicit Kirk-Mann (IKM)(8)] iterative schemes with the help of computer programs in PYTHON 2.5.4. We shall consider our results for increasing and decreasing functions. The results are shown in Table 1 and Table 2.
3.1. Example of Increasing Function (See 5.12 of [4] )
Let 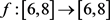 be defined by
be defined by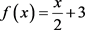 . Then f is an increasing function with fixed point
. Then f is an increasing function with fixed point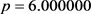 . By taking initial approximation as
. By taking initial approximation as 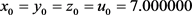 (mid point of x and y) and
(mid point of x and y) and 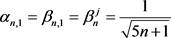 , (for
, (for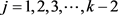 ),
), 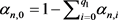 ,
, 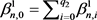 ,
,  ,
, 

3.2. Example of Decreasing Function (See 5.11 of [4] )
Let 










Table 1. Numerical example for increasing function:
Table 2. Numerical example for decreasing function:
4. Remark
i) From Table 1, it is observed that for increasing function
convergence of implicit Kirk-multistep iterative scheme (2) to the fixed point 6.000000 is equivalent to the convergence of other implicit Kirk-type [implicit Kirk-Noor (IKN) (6), implicit Kirk-Ishikawa (IKI) (7) and implicit Kirk-Mann (IKM) (8)] iterative schemes to the same fixed point 6.000000;
ii) from Table 2, it is observed that for decreasing function
5. Conclusion
The numerical examples considered in this paper justified our claim on the equivalence results obtained. These results show that our implicit Kirk-type hybrid iterative schemes have good potentials for further applications.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Bosede, A.O., Akewe, H., Bakre, O.F. and Wusu, A.S. (2019) On the Equivalence of Implicit Kirk-Type Fixed Point Iteration Schemes for a General Class of Maps. Journal of Applied Mathematics and Physics, 7, 123-137. https://doi.org/10.4236/jamp.2019.71011
References
- 1. Olatinwo, M.O. (2008) Some Stability Results for Two Hybrid Fixed Point Iterative Algorithms of Kirk-Ishikawa and Kirk-Mann Type. Journal of Advanced Mathematical Studies, 1, 87-96.
- 2. Chugh, R. and Kumar, V. (2012) Stability of Hybrid Fixed Point Iterative Algorithms of Kirk-Noor Type in Normed Linear Space for Self and Nonself Operators. International Journal of Contemporary Mathematical Sciences, 7, 1165-1184.
- 3. Akewe, H., Okeke, G.A. and Olayiwola, A. (2014) Strong Convergence and Stability of Kirk-Multistep-Type Iterative Schemes for Contractive-Type Operators. Fixed Point Theory Appications, 45, 24 p.
- 4. Chugh, R., Malik, P. and Kumar, V. (2015) On a New Faster Implicit Fixed Point Iterative Scheme in Convex Metric Space. Journal of Function Spaces, Article ID: 905834.
- 5. Bosede, A.O. and Rhoades, B.E. (2010) Stability of Picard and Mann Iteration for a General Class of Functions. Journal of Advanced Mathematical Studies, 3, 1-3.
- 6. Zamfirescu, T. (1972) Fixed Point Theorems in Metric Spaces. Archiv der Mathematik (Basel), 23, 292-298. https://doi.org/10.1007/BF01304884
- 7. Osilike, M.O. (1995) Stability Results for Ishikawa Fixed Point Iteration Procedure. Indian Journal of Pure and Applied Mathematics, 26, 937-941.
- 8. Rhoades, B.E. (1990) Fixed Point Theorems and Stability Results for Fixed Point Iteration Procedures. Indian Journal of Pure and Applied Mathematics, 21, 1-9.
- 9. Imoru, C.O. and Olatinwo, M.O. (2003) On the Stability of Picard and Mann Iteration. Carpathian Journal of Mathematics, 19, 155-160.
- 10. Chidume, C.E. and Olaleru, J.O. (2014) Picard Iteration Process for a General Class of Contractive Mappings. Journal of Nigerian Mathematical Society, 33, 19-23.
- 11. Berinde, V. (2004) On the Convergence of Ishikawa Iteration in the Class of Quasi Contractive Operators. Acta Mathematica Universitatis Comenianae, 73, 119-126.
- 12. Soltuz, S.M. (2005) The Equivalence of Picard, Mann and Ishikawa Iterations Dealing with Quasi-Contractive Operators. Mathematical Communications, 10, 81-88.


