Received 6 April 2015; accepted 24 May 2015; published 27 May 2015

ABSTRACT

In this paper, the kinetic energy formula was expressed during one-parameter closed planar homothetic inverse motions in complex plane. Then the relation between the kinetic energy formula and the Steiner formula was given. As an example the sagittal motion of a telescopic crane was considered. This motion was described by a double hinge consisting of the fixed control panel of telescopic crane and the moving arm of telescopic crane. The results were applied to experimentally measured motion.

Keywords:

Steiner Formula, Kinetic Energy, Inverse Motions, Planar Kinematics, Homothetic Motions

1. Introduction

For a geometrical object rolling on a line and making a complete turn, some properties of the area of a path of a point were given by [1] . The Steiner area formula and the Holditch theorem during one parameter closed planar homothetic motions were expressed by [2] . If the points of the moving planes which enclose the same area lie on a circle, then the centre of this circle is called the Steiner point (h = 1) [3] [4] . Dathe H. and Gezzi R. expressed the formula of kinetic energy for the closed planar kinematics [5] . The formula of kinetic energy for the closed planar homothetic inverse motion was expressed by [6] . In our previous paper, the Steiner formula and the polar moment of inertia for the closed planar homothetic inverse motions were given in complex plane [7] . In this paper, we calculated the expression of the kinetic energy formula under one parameter closed planar homothetic inverse motions in complex plane. Furthermore, we expressed the relation between the area enclosed by a path and the kinetic energy. In the case of the homothetic scale the results given by [5] were obtained as a special case. As an example, Dathe H. and Gezzi R. have chosen the sagittal part of the movement of the human leg during walking for planar kinematics [8] . We considered the sagittal motion of a telescopic crane which was described by a double hinge being fixed and moving as an example. The kinetic energy formula was calculated for this motion. Moreover, the relation between the kinetic energy and the Steiner formula was expressed.

2. The Kinetic Energy in Planar Homothetic Inverse Motion

We consider one parameter closed planar homothetic motion between two reference systems: the fixed 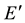and the moving E, with their origins 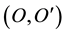and orientations. Then, we take into account motion relative to the moving coordinate system (inverse motion). We know the motion defined by the transformation

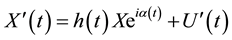
is called one-parameter closed planar homothetic direct motion in complex plane.

By taking displacement vector and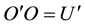, the total angle of rotation, the motion defined by the transformation

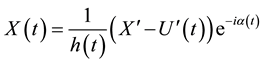(1)

is called one-parameter closed planar homothetic inverse motion in complex plane and denoted by, where h is a homothetic scale of the motion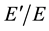, X and 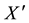are the position vectors with respect to the moving and fixed rectangular coordinate systems of a point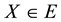, respectively. The homothetic scale h and the vector X and are continuously differentiable functions of a real parameter t.

In Equation (1), is the trajectory with the respect to the moving system of a point belonging to the fixed system.

If we consider the below coordinates of Equation (1)

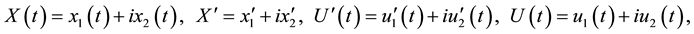
we can write

(2)

From Equation (2), the components of may be given as

(3)

If we show the coordinates of the Equation (1)

(4)

and the rotation matrice

(5)

we can obtain

(6)

From Equation (3), by differentiation with respect to t, we have

(7)

A moment with a first order in the time derivatives can be introduced by

(8)

which is the integral over the kinetic energy of a point with mass.

Using Equation (7) we can calculate the equation

(9)

If Equation (9) is replaced in Equation (8),

(10)

is obtained.

If is taken, then for the formula of kinetic energy of the origin point we have

(11)

If Equation (11) is replaced in Equation (10),

(12)

can be written.

For, we have

[8] (14)

If Equation (14) of [8] is respectively replaced at coefficients of and in Equation (10) and by calculating necessary operations,

(13)

is obtained.

Now we consider the case in which the motion is closed and naturally parametrized. Then, it follows

, and. With those assumptions, we obtain

(14)

If we consider the equations

[8] (9)

[8] (11)

and

[8] (12)

and Equations (9), (11) and (12) of [8] are replaced in Equation (14),

(15)

is arrived at the relation between the formula of kinetic energy and the formula for the area.

3. Application: The Inverse Motion of Telescopic Crane

The motion of telescopic crane has a double hinge and “a double hinge” means that it has two systems a fixed arm and a moving arm of telescopic crane (Figure 1). There is a control panel of telescopic crane at the origin of fixed system. “L” arm can extend or retract by h parameter. Also we consider (Equation (12) of [8] ). Now we use it for this section.

If we calculate the time derivative of the equation

[8] (37)

we obtain

(16)

(17)

We must calculate for the formula of kinetic energy in Equation (8). So then, in Section 3.1 of [8] , we integrate the previous equation using periodic boundary conditions while assuming that the integrands are

periodic functions. The periodicity of f implies that integrals of the following types vanish.

If we calculate the time derivative of the equation

[8] (36)

we have

(18)

Then if Equation (36) of [8] and Equation (18) are replaced in calculating data and in Section 2, by using the parameters;

(19)

is obtained.

If we consider the equations

[8] (41)

and

[8] (42)

and Equations (41) and (42) of [8] are replaced in Equation (19), then

(20)

is arrived at the relation between the formula of kinetic energy and the area formula for application.

References