American Journal of Computational Mathematics
Vol.05 No.03(2015), Article ID:59492,6 pages
10.4236/ajcm.2015.53030
Adomian Decomposition Approach to the Solution of the Burger’s Equation
Iyakino P. Akpan
Department of Basic Science, College of Agriculture, Lafia, Nigeria
Email: akpanip@yahoo.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 July 2015; accepted 6 September 2015; published 9 September 2015
ABSTRACT
Adomian decomposition method is presented as a method for the solution of the Burger’s equation, a popular PDE model in the fluid mechanics. The method is computationally simple in application. The approximate solution is obtained by considering only the first two terms of the decomposition in this paper. Numerical experimentation shows accuracy of a minimum error of order five for various space steps and coefficient of kinematic viscosity. The method is considered high in accuracy.
Keywords:
Adomian Decomposition, Burger’s Equation, Kinematic Viscosity, Nonlinear Operators

1. Introduction
Burger’s equation is a fundamental partial differential equation in fluid mechanics. It is also a very important model encountered in several areas of applied mathematics such as heat conduction, acoustic waves, gas dynamics and traffic flow [1] . Analytical solutions of the partial differential equations modeling physical phenomena exist only in few of the cases. Therefore the need for the construction of efficient numerical methods for the approximate solution of these models always exists. Many of the analytical solutions to the Burger’s equation involve Fourier series. According to [2] , the convergence of such Fourier-series based solutions is very slow. Several researchers have proposed various numerical methods for the solution of the Burger’s equation. [3] and [4] used the finite element method for the solution of the Burger’s equation. [5] and [6] used the finite difference method. [7] used the direct variational method while [8] used the projection method by B-spline.
A decomposition method which provides convergent solutions to nonlinear stochastic operator equations was developed in [9] . [10] gave proof of convergence of Adomian decomposition method when applied to differential equations. [11] constructed an algorithm for solving nonlinear equations based on Newton-Raphson method using Adomian decomposition approach. In an effort to extend the usefulness of Adomian’s decomposition method into other areas of mathematics, [12] developed a technique for calculating Adomian’s polynomials for nonlinear operators. [13] presented a method for the solution of homogeneous differential equations using Adomian’s decomposition without noisy terms. [14] extended the application of the Adomian decomposition method for the calculations of non-differential functions.
In this paper, presentation of a numerical method for the solution of the nonlinear reaction-diffusion Burger’s equation using Adomian decomposition is made. The organization of this paper is as follows: in Section 2 the theoretical approach is presented. In Section 3 the Adomian’s polynomials for the Burger’s equation are determined. In Section 4 computational results for the Burger’s equation using Adomian’s decomposition are presented while conclusion is presented in Section 5.
2. Theoretical Approach
Consider the Burger’s equation
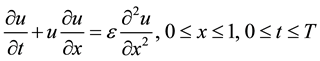 (1)
(1)
Subject to initial condition
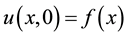 (2)
(2)
And boundary conditions:
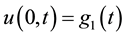 (3)
(3)
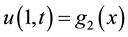 (4)
(4)
Defining the operators:
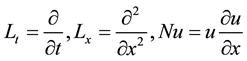 (5)
(5)
Equation (1) can be written as:
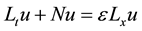 (6)
(6)
Solving Equation (6) for 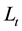 and
and 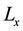 respectively gives
respectively gives
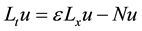 (7)
(7)
and
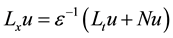 (8)
(8)
where 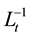 and
and 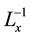 are the inverse operators of
are the inverse operators of 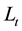 and
and 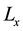 given respectively as:
given respectively as:
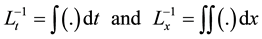 (9)
(9)
Operating both sides of Equations (7) and (8) with the inverse operators (9) we obtain:
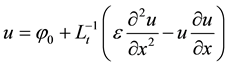 (10)
(10)

where

and

Adding Equations (10) and (11) and dividing by 2, gives the canonical form:

The parameterized form of (14) is

where

According to [15] the parameterized decomposition forms of and Nu are:


An are the Adomian’s polynomials which can be generated for all types of nonlinearities [16] .
Substituting Equations (17) and (18) into Equation (15) gives

Expanding both sides of Equation (19) gives

By comparing coefficients of both hand sides of Equation (20), it is obtained that:
From which we establish the recursive relation

3. Determination of Adomian’s Polynomials
The Adomian’s polynomials, 

Substituting Equation (17) into Equation (18) and expanding the RHS gives

From Equation (22), we establish that the Adomian’s polynomials have the following forms:
The Adomian’s polynomials for Equation (1) are obtained from the recurrent relation

4. Numerical Experiment
We present numerical results to illustrate the effectiveness of the proposed method. Consider Burger’s Equation (1) with the following initial and boundary conditions.
The exact solution of Equation (1) with the above conditions was given in [1] as
Computations of Absolute and Relative Errors
Absolute errors of the method were computed by use of the formula:
where the numerical solution at the grid point 


Relative errors were computed by use of the formula:
where the numerical solution at the grid point 


Figure 1 is a 3 dimensional plot of the surface 
5. Conclusion
In this paper, Adomian decomposition method is used to solve the burger’s equation numerically. From Table 1 and Table 2, this method is considered to give accurate results for specified values of the parameter, ε. We considered the first two terms of the decomposition to make the approximate solution. Accuracy of the method
Figure 1. A 3 dimensional plot of the surface
Figure 2. A 3 dimensional plot of the surface
Table 1. Approximate solutions by Adomian’s decomposition, errors and relative errors for t = 0.2, e = 0.001, a = 2.
Table 2. Approximate solutions by Adomian’s decomposition, errors and relative errors for t = 0.05, e = 0.01, a = 2.
can be improved by considering more terms in the solution approximation. All computations were carried out using Maple 15.
Cite this paper
Iyakino P.Akpan, (2015) Adomian Decomposition Approach to the Solution of the Burger’s Equation. American Journal of Computational Mathematics,05,329-335. doi: 10.4236/ajcm.2015.53030
References
- 1. Maleknejad, K., Babolian, E., Shaerlar, A.J. and Jahnagir, M. (2011) Operational Matrices for Solving Burgers Equation by Using Block-Pulse Functions with Error Analysis. Australian Journal of Basic and Applied Sciences, 5, 602-609.
- 2. Aksan, E.N., Ozdes, A. and Ozia, T. (2006) A Numerical Solution of Burger’s Based Squares Approximation. Applied Mathematics and Computation, 176, 270-279.
http://dx.doi.org/10.1016/j.amc.2005.09.045 - 3. Varoglu, E. and Finn, W.D.L. (1980) Space-Time Finite Elements Incorporating Characteristics for Burger’s Equation. International Journal for Numerical Methods in Engineering, 16, 171-184.
http://dx.doi.org/10.1002/nme.1620160112 - 4. Caldwell, J., Wanless, P. and Cook, A.E. (1981) A Finite Element Approach to Burger’s Equation. Applied Mathematical Modelling, 5, 189-193.
http://dx.doi.org/10.1016/0307-904X(81)90043-3 - 5. Smith, G.D. (1989) Numerical Solution of Partial Differential Equations. Oxford Press, Oxford.
- 6. Ames, W.F. (1992) Numerical Methods for Partial Differential Equations. Academic Press, New York.
- 7. Ozas, T. and Ozdes, A. (1996) A Direct Variational Method Applied to Burgers Equation. Journal of Computational and Applied Mathematics, 71, 163-175.
http://dx.doi.org/10.1016/0377-0427(95)00221-9 - 8. Dag, J., Saka, B. and Boz, A. (2005) B-Splin Galekin Method for Numerical Solutions of the Burgers Equation. Applied Mathematics and Computation, 166, 506-522.
http://dx.doi.org/10.1016/j.amc.2004.06.078 - 9. Adomian, G. (1986) Nonlinear Stochastic Operator Equations. Academic Press, New York.
- 10. Abbaoui, K. and Cherruault, Y. (1994) Convergence of Adomian’s Method Applied to Differential Equations. Computers & Mathematics with Applications, 28, 103-109.
http://dx.doi.org/10.1016/0898-1221(94)00144-8 - 11. Abbasbandy, S. (2003) Improving Newton-Raphson Method for Nonlinear Equations by Modified Adomian Decomposition Method. Applied Mathematics and Computation, 145, 887-893.
http://dx.doi.org/10.1016/S0096-3003(03)00282-0 - 12. Chen, W. and Lu, Z. (2004) An Algorithm for Adomian Decomposition Method. Applied Mathematics and Computation, 170, 570-583.
http://dx.doi.org/10.1016/j.amc.2003.10.037 - 13. Gharsseldien, Z.M. and Hemida, K. (2009) New Technique to Avoid Noise Terms on the Solution of Inhomogeneous Differential Equations by Using Adomian Decomposition Method. Communication in Nonlinear Science and Numerical Simulation, 14, 685-696.
http://dx.doi.org/10.1016/j.cnsns.2007.11.018 - 14. Wu, G.C. (2011) Adomian Decomposition Method for Non-Smooth Initial Value Problems. Mathematical and Computer Modeling, 54, 2104-2108.
http://dx.doi.org/10.1016/j.mcm.2011.05.018 - 15. Mamaloukas, C. (2000) An Approximate Solution of Burgers Equation Using Adomian’s Decomposition Method. Proceedings of the Conference of Applied Differential Geometry—General Relativity and the Workshop on Global Analysis, Differential Geometry and Lie Algebra, Balkan Press, 88-98.
- 16. Adomian, G. (1989) Nonlinear Stochastic Systems Theory and Application to Physics. Kluwer Academic Publishers, Netherlands.
http://dx.doi.org/10.1007/978-94-009-2569-4 - 17. Bhadauria, R., Singh, A.K. and Singh, D.P. (2012) Solution of Reaction-Diffusion Equation by Adomian Decomposition Method. International Journal of Engineering Science and Technology, 4, 2626-2630.
















