J. Software Engineering & Applications, 2009, 2: 375-382
doi:10.4236/jsea.2009.25050 Published Online December 2009 (http://www.SciRP.org/journal/jsea)
375
Endurance Analysis of Automotive Vehicle’s Door
W/H System Using Finite Element Analysis
Byeong-Sam Kim1, Kyoungwoo Park2, Young-Woo Kim1
1Department of Automotive Eng., Hoseo University, Asan, Korea; 2Department of Mechanical Eng., Hoseo University, Asan, Korea.
Received June 4th, 2009; revised July 15th, 2009; accepted August 26th, 2009.
ABSTRACT
In the automotive electronics industry, demand for low-cost, high strength-to in-service performance for electronic
components continues to drive the development of vehicles’ door Wiring Harness (W/H) system for new applications.
The problem of the fatigue strength estimation of materials or components containing natural defects, inclusions or in
homogeneities is of great importance from both a scientific and industrial point of view. This article gives some insight
into the dimensioning process, with special focusing on fatigue analysis of W/H in a vehicle’s door structures. An en-
durance life prediction of door W/H was calculated using finite element analyses. Endurance test data for slim test
specimens were compared with the predicted fatigue life for verification. The final life expectancy of the component
combines the effects of these microstructural features with the complex stress state arising from the combined service
loading and residual stresses.
Keywords: Endurance, Wiring Harness System, Finite Element Analysis
1. Introduction
An automotive electronic system must be able to antici-
pate the need for reliable and cost effective connection
systems. A vehicle’s Wiring Harness (W/H) system
keeps everything else going, powering every component,
every switch, and every device. It’s the vehicle’s central
nervous system. It must work every time and all the time.
Without the connection system, no system will work; it
will play a vital role in any industry, not only the auto-
motive. The main function of the door connection system
is to distribute the power supply from one system to an-
other system. In automotive cars, it requires a lot of wir-
ing harness systems to distribute the power from one
system to another. Any wiring harness should have suffi-
cient strength to withstand any abrupt situations without
affecting the performance of the total system. Figure 1
shows the typical wiring harness system of the front por-
tion of the car.
In a vehicle’s door Wiring Harness (W/H) system, it is
more preferred to arranging a passenger compartment
than a hinge and a weatherstrip. An opening/closing
member is attached to a vehicle by a hinge enabling easy
opening and closing of the different moving member.
Such members include doors, such as side-doors and rear
doors, and other opening/closing members, such as trunk
lids. A guide member made of an elastic material has an
accurate portion which can extend and contract while
twisting. The problem of the fatigue strength estimation
of materials or components containing natural defects,
inclusions or inhomogeneities is of great importance
from both scientific and industrial point of view in Figure
1. Automotive Wiring Harness (W/H) system is arranged
between a door and a body of the vehicle after being
mounted on the guide members, and the opposite ends of
the guide members are fixed to both the door and the
body, so that the movements of the guide member and
the wiring harness can follow the opening and closing
1. ENG JB-ENG
2. RLY BOX-ENG
3. Front Door Grommet
4. Rear Door Grommet
5.Under Steering Column
6. Trunk Read
7. Under Seat
Figure 1. Automotive Wiring Harness (W/H) system

Endurance Analysis of Automotive Vehicle’s Door W/H System Using Finite Element Analysis 376
Endurance Analysis
Endurance (Life prediction)
① Slam Test Spec. &
Specification
② Tester
③ Prototype
④ Slam Test
Endurance Bending Analysis
Procedure
Failure Mode
Endurance Analysis
Endurance (Life prediction)
Analysis/test results
comparison/verification
Selection
Endurance Test
Failure Type
Mode Analysis
Data Select by Verification
and Identification of the
decision criteria
Design Change
CAD Type
Return
Report/End
Bending Test
(Temp. change)
① Mesh Generation
② Contact
③ Material Property
④ B.C. and Load
⑤ Parameter Set
① Select of Part
② 3D Modeling
③ IGES/STEP Change
④ CAD Compatibility
Figure 2. Diagram for analysis procedure
movements of the door. The wiring harness system must
not only conform to such mechanical performance re-
quirements; like strength, engage force, mating force,
durability, but also to electrical performance require-
ments like low level termination resistance, voltage drop,
isolation resistance, and temperature rise. Further, com-
pliance is also required in environmental performance
requirements, like voltage and temperature range, ther-
mal cycling, temperature /humidity cycling, mechanical
shock, vibration, salt fog immersion, and fatigue com-
patibility.
However, when following the above-noted open-
ing/closing operation, W/H system was a problem of the
fatigue, where a tube, grommet, copper etc after 1 or 5
x105 cycle. This paper gives some insight into the di-
mensioning process, with special focusing on fatigue
analysis of W/H in vehicle’s door structures [3]. An en-
durance life prediction of door W/H used finite element
analyses and slim tester (Figure 2).
2. Endurance Analysis of Flexible Bending
2.1 Definition of Model
The large deflection problem considered in this study is
the behaviour of front door due to the physical JIG de-
sign for test results performance, reliability data for
analysis. Figure 1 shows extracted from the body and
door structure of the wire line as a reference guide to use
sweep capabilities to create a solid model. The scope of
this work into develops a slam tester method. The slam
tester is designed by Packard Korea in collaboration with
GM-Daewoo. An endurance life prediction of door W/H
is used finite element analyses and slim tester [4]. In
automotive industry a long development period is neces-
sary to secure the safety and the reliability of the vehicle
within acceptable fatigue and durability parameters.
2.2 FEM Modeling for W/H
Each of the finite element models created for the differ-
ent test configurations in this work was developed with a
computer-aided design pre-processor. The W/H front
door finite element models had the same cable bundle
configuration as the samples used in the experimental
tests. Some geometrical assumptions were used to repre-
sent the W/H and to simplify the 3D model. We estimate
that the stiffeners of the outside tape are negligible. Fig-
ure 3(a) shows the 3D model of the bundle composed of
19 wires of 0.19 mm diameter. The deformed configura-
tion of the cables is presented in Figure 3(b). Each time
the door is opened or closed the W/H is subjected to
combined tension/bending loading. Hence a nonlinear
large deflection analysis needs to be performed to find
out the resulting plastic deformation after the towing
loads are removed.
(a) Number of cable 19 with 0.19 mm (b) Wire twist with contact
Figure 3. FE 3D Model for wire harness and cable with boundary condition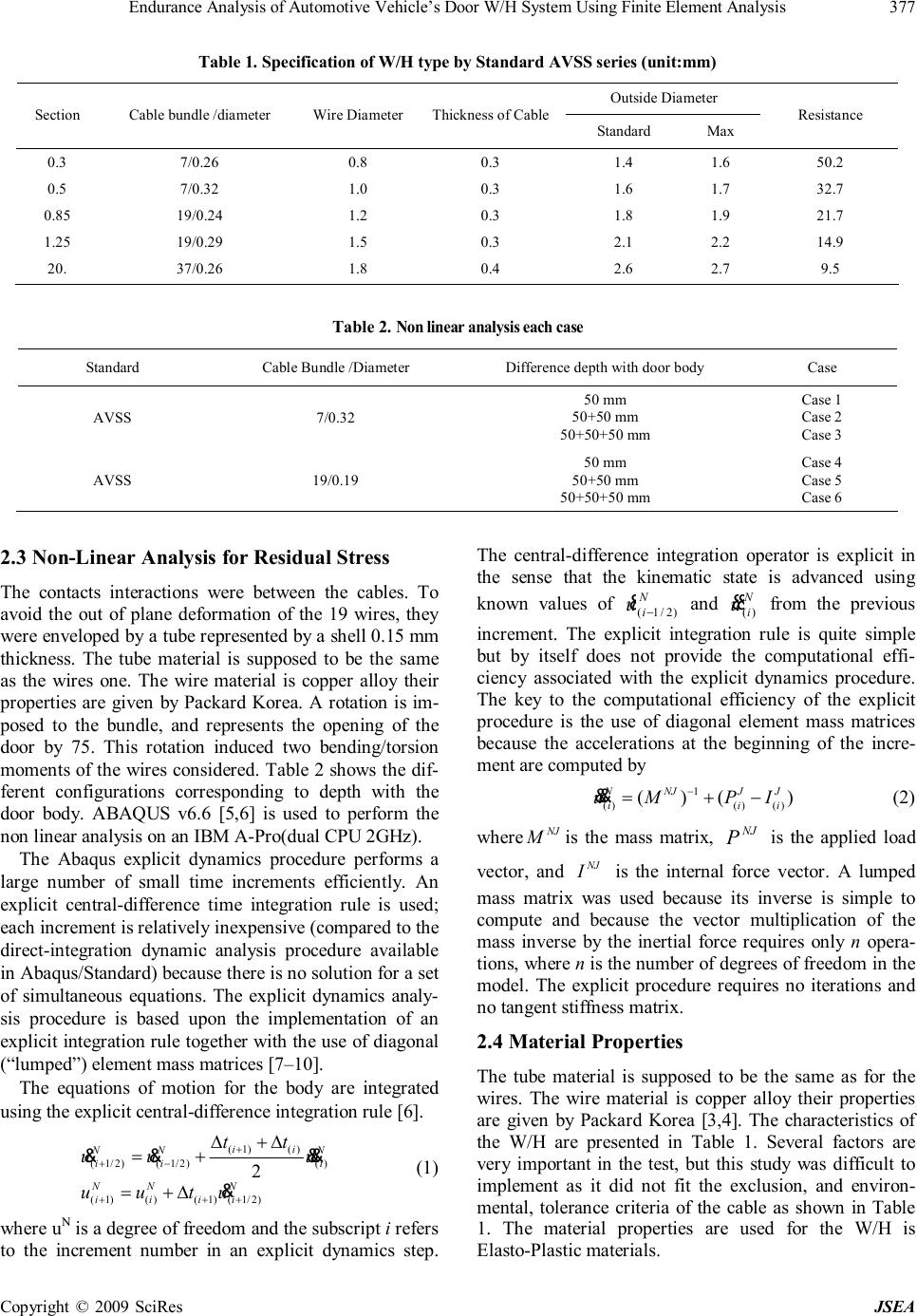

Endurance Analysis of Automotive Vehicle’s Door W/H System Using Finite Element Analysis 377
Table 1. Specification of W/H type by Standard AVSS series (unit:mm)
Outside Diameter
Section Cable bundle /diameter Wire Diameter Thickness of Cable Standard Max Resistance
0.3 7/0.26 0.8 0.3 1.4 1.6 50.2
0.5 7/0.32 1.0 0.3 1.6 1.7 32.7
0.85 19/0.24 1.2 0.3 1.8 1.9 21.7
1.25 19/0.29 1.5 0.3 2.1 2.2 14.9
20. 37/0.26 1.8 0.4 2.6 2.7 9.5
Table 2.
Non linear analysis each case
Standard Cable Bundle /Diameter Difference depth with door body Case
AVSS 7/0.32 50 mm
50+50 mm
50+50+50 mm
Case 1
Case 2
Case 3
AVSS 19/0.19 50 mm 50+50 mm
50+50+50 mm
Case 4
Case 5
Case 6
2.3 Non-Linear Analysis for Residual Stress
The contacts interactions were between the cables. To
avoid the out of plane deformation of the 19 wires, they
were enveloped by a tube represented by a shell 0.15 mm
thickness. The tube material is supposed to be the same
as the wires one. The wire material is copper alloy their
properties are given by Packard Korea. A rotation is im-
posed to the bundle, and represents the opening of the
door by 75. This rotation induced two bending/torsion
moments of the wires considered. Table 2 shows the dif-
ferent configurations corresponding to depth with the
door body. ABAQUS v6.6 [5,6] is used to perform the
non linear analysis on an IBM A-Pro(dual CPU 2GHz).
The Abaqus explicit dynamics procedure performs a
large number of small time increments efficiently. An
explicit central-difference time integration rule is used;
each increment is relatively inexpensive (compared to the
direct-integration dynamic analysis procedure available
in Abaqus/Standard) because there is no solution for a set
of simultaneous equations. The explicit dynamics analy-
sis procedure is based upon the implementation of an
explicit integration rule together with the use of diagonal
(“lumped”) element mass matrices [7–10].
The equations of motion for the body are integrated
using the explicit central-difference integration rule [6].
(1)()
(1/2)(1/2)()
(1)()(1)(1/2)
2
ii
NNN
iii
NNN
iiii
tt
uuu
uutu
+
+−
+++
∆+∆
=+
=+∆
&&&&
& (1)
where uN
N is a degree of freedom and the subscript i refers
to the increment number in an explicit dynamics step.
The central-difference integration operator is explicit in
the sense that the kinematic state is advanced using
known values of N
i
u)2/1( −
&
and N
i
u)(
&
&
from the previous
increment. The explicit integration rule is quite simple
but by itself does not provide the computational effi-
ciency associated with the explicit dynamics procedure.
The key to the computational efficiency of the explicit
procedure is the use of diagonal element mass matrices
because the accelerations at the beginning of the incre-
ment are computed by
1
()()()
()()
NNJJJ
iii
uMPI
−
=+−
&&
(2)
where
NJ
Mis the mass matrix, NJ
P is the applied load
vector, and
NJ
I
is the internal force vector. A lumped
mass matrix was used because its inverse is simple to
compute and because the vector multiplication of the
mass inverse by the inertial force requires only n opera-
tions, where n is the number of degrees of freedom in the
model. The explicit procedure requires no iterations and
no tangent stiffness matrix.
2.4 Material Properties
The tube material is supposed to be the same as for the
wires. The wire material is copper alloy their properties
are given by Packard Korea [3,4]. The characteristics of
the W/H are presented in Table 1. Several factors are
very important in the test, but this study was difficult to
implement as it did not fit the exclusion, and environ-
mental, tolerance criteria of the cable as shown in Table
1. The material properties are used for the W/H is
Elasto-Plastic materials.

Endurance Analysis of Automotive Vehicle’s Door W/H System Using Finite Element Analysis 378
(a) Stresses distribution (b) Maximum deflection of cable wire
Figure 4. Non linear analysis with stress distribution and deflection in case2 (ABAQUS)
(a) Stresses distribution (b) Maximum deflection of cable wire
Figure 5. Non linear analysis with stress distribution and deflection in case 5 (ABAQUS)
Figures 4 and 5 show the difference of depth with
front door body. This means that a larger number of ca-
bles with wire are not less than the variation mode then it
is a lot of more flexible and also stresses that the work
can be seen. In addition, if the same contribute with cable
larger depth with door body stresses that the work can be
found in Table 4.
2.5 Durability Analysis with Flexible Bending
The history of cycle loading can be considered as a sine
curve and corresponding to opening/closing of the door
by 75. Figures 6 and 7 present the damage criteria over
the wires. A value of 1 for these criteria indicates that a
crack has occurred. The life cycle obtained by the ex-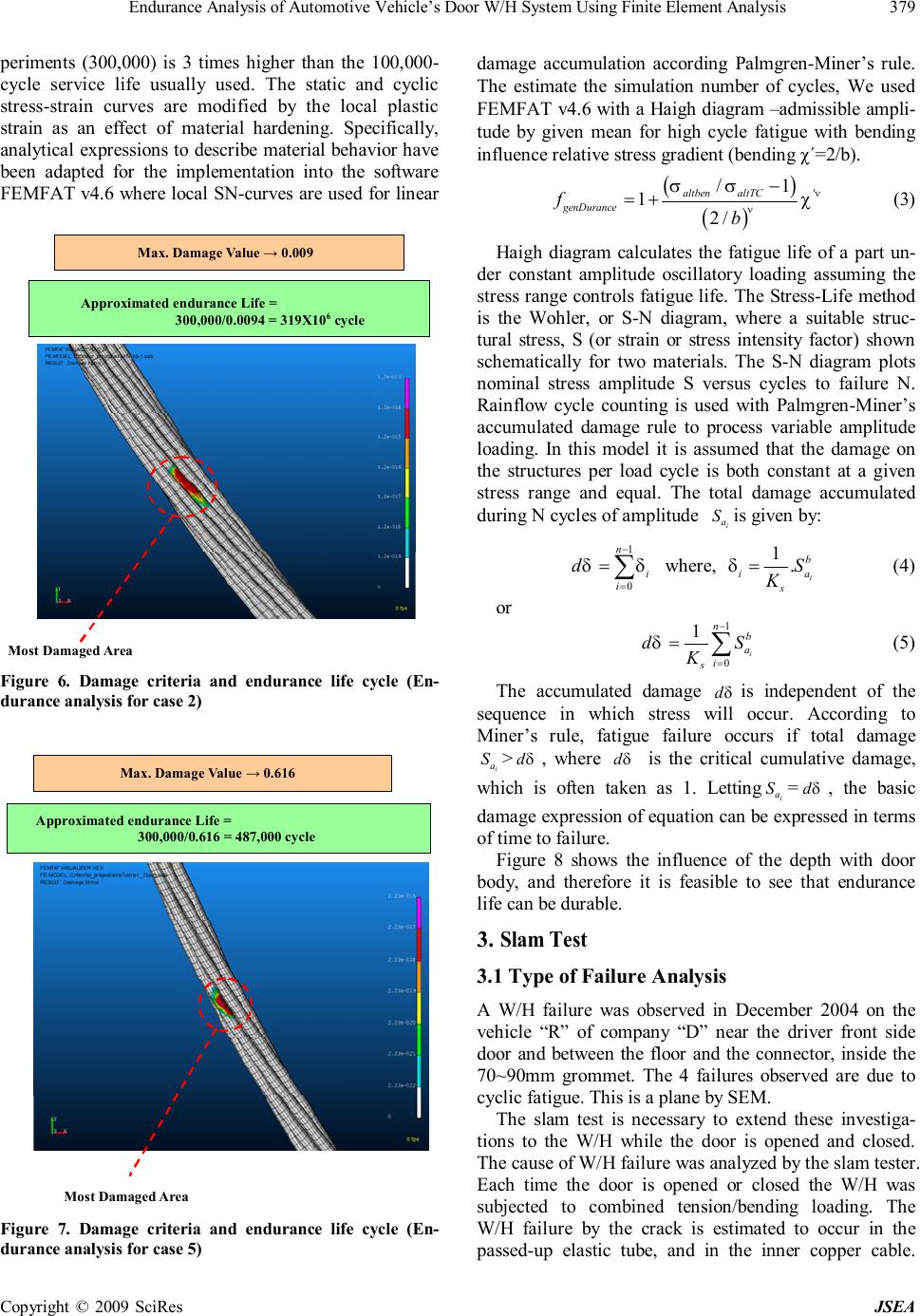

Endurance Analysis of Automotive Vehicle’s Door W/H System Using Finite Element Analysis 379
periments (300,000) is 3 times higher than the 100,000-
cycle service life usually used. The static and cyclic
stress-strain curves are modified by the local plastic
strain as an effect of material hardening. Specifically,
analytical expressions to describe material behavior have
been adapted for the implementation into the software
FEMFAT v4.6 where local SN-curves are used for linear
Most Damaged Area
Approximated endurance Life =
300,000/0.0094 = 319X10
6
cycle
Max. Damage Value → 0.009
Figure 6. Damage criteria and endurance life cycle (En-
durance analysis for case 2)
Approximated endurance Life
=
300,000/0.616 = 487,000 cycle
Most Damaged Area
Max. Damage Value → 0.616
Figure 7. Damage criteria and endurance life cycle (En-
durance analysis for case 5)
damage accumulation according Palmgren-Miner’s rule.
The estimate the simulation number of cycles, We used
FEMFAT v4.6 with a Haigh diagram –admissible ampli-
tude by given mean for high cycle fatigue with bending
influence relative stress gradient (bending χ´=2/b).
(
)
( )
'
/1
12/
altbenaltTC
genDurance
fb
ν
ν
σσ
χ
−
=+ (3)
Haigh diagram calculates the fatigue life of a part un-
der constant amplitude oscillatory loading assuming the
stress range controls fatigue life. The Stress-Life method
is the Wohler, or S-N diagram, where a suitable struc-
tural stress, S (or strain or stress intensity factor) shown
schematically for two materials. The S-N diagram plots
nominal stress amplitude S versus cycles to failure N.
Rainflow cycle counting is used with Palmgren-Miner’s
accumulated damage rule to process variable amplitude
loading. In this model it is assumed that the damage on
the structures per load cycle is both constant at a given
stress range and equal. The total damage accumulated
during N cycles of amplitude
i
a
S
is given by:
1
0
n
i
i
d
δδ
−
=
=
∑
where, 1
.
i
b
ia
s
S
K
δ= (4)
or 1
0
1
i
n
b
a
i
s
dS
K
δ−
=
=
∑
(5)
The accumulated damage
d
δ
is independent of the
sequence in which stress will occur. According to
Miner’s rule, fatigue failure occurs if total damage
i
a
S
>
d
δ
, where
d
δ
is the critical cumulative damage,
which is often taken as 1. Letting
i
a
S
=
d
δ
, the basic
damage expression of equation can be expressed in terms
of time to failure.
Figure 8 shows the influence of the depth with door
body, and therefore it is feasible to see that endurance
life can be durable.
3. Slam Test
3.1 Type of Failure Analysis
A W/H failure was observed in December 2004 on the
vehicle “R” of company “D” near the driver front side
door and between the floor and the connector, inside the
70~90mm grommet. The 4 failures observed are due to
cyclic fatigue. This is a plane by SEM.
The slam test is necessary to extend these investiga-
tions to the W/H while the door is opened and closed.
The cause of W/H failure was analyzed by the slam tester.
Each time the door is opened or closed the W/H was
subjected to combined tension/bending loading. The
W/H failure by the crack is estimated to occur in the
passed-up elastic tube, and in the inner copper cable.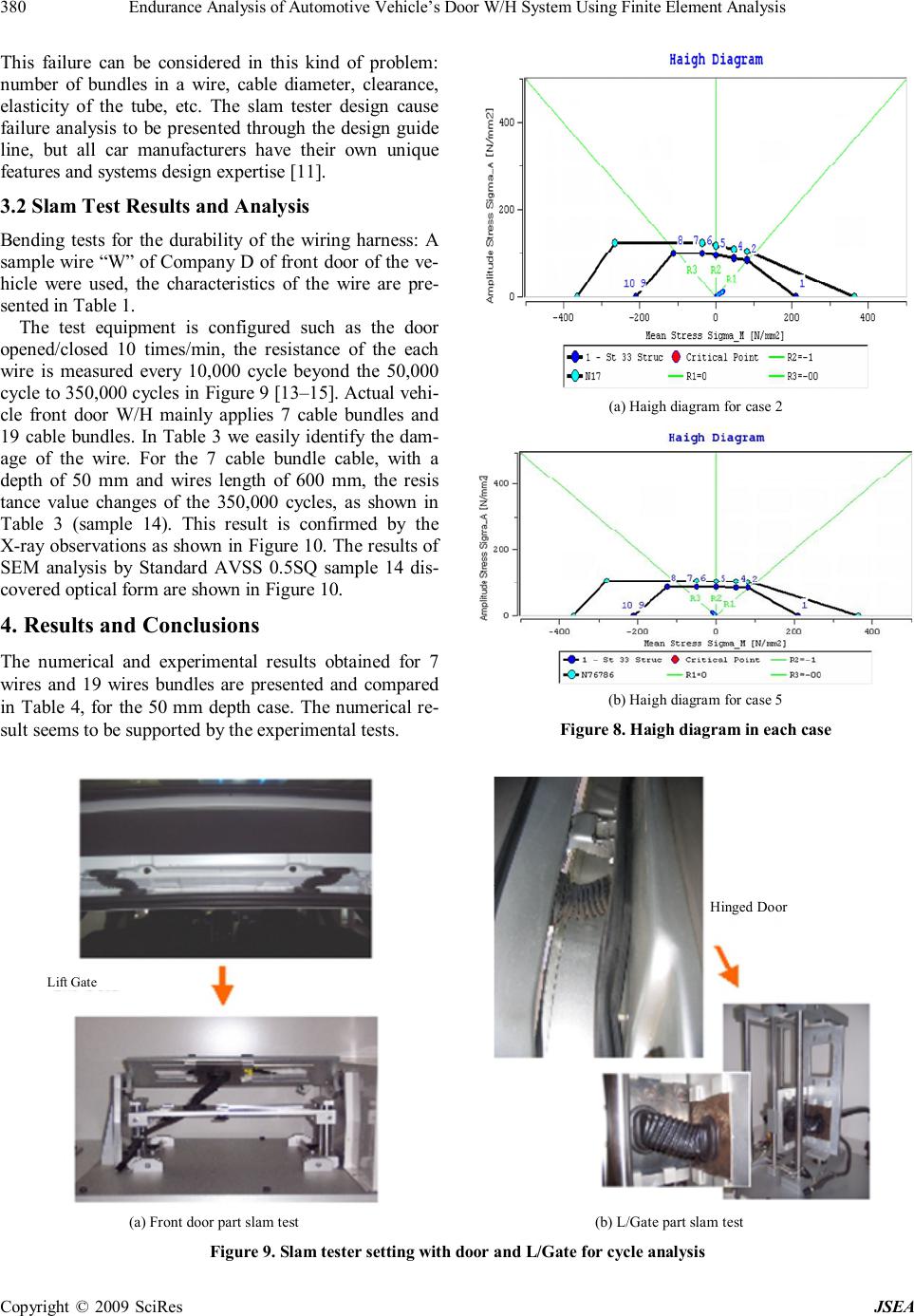

Endurance Analysis of Automotive Vehicle’s Door W/H System Using Finite Element Analysis 380
This failure can be considered in this kind of problem:
number of bundles in a wire, cable diameter, clearance,
elasticity of the tube, etc. The slam tester design cause
failure analysis to be presented through the design guide
line, but all car manufacturers have their own unique
features and systems design expertise [11].
3.2 Slam Test Results and Analysis
Bending tests for the durability of the wiring harness: A
sample wire “W” of Company D of front door of the ve-
hicle were used, the characteristics of the wire are pre-
sented in Table 1.
The test equipment is configured such as the door
opened/closed 10 times/min, the resistance of the each
wire is measured every 10,000 cycle beyond the 50,000
cycle to 350,000 cycles in Figure 9 [13–15]. Actual vehi-
cle front door W/H mainly applies 7 cable bundles and
19 cable bundles. In Table 3 we easily identify the dam-
age of the wire. For the 7 cable bundle cable, with a
depth of 50 mm and wires length of 600 mm, the resis
tance value changes of the 350,000 cycles, as shown in
Table 3 (sample 14). This result is confirmed by the
X-ray observations as shown in Figure 10. The results of
SEM analysis by Standard AVSS 0.5SQ sample 14 dis-
covered optical form are shown in Figure 10.
4. Results and Conclusions
The numerical and experimental results obtained for 7
wires and 19 wires bundles are presented and compared
in Table 4, for the 50 mm depth case. The numerical re-
sult seems to be supported by the experimental tests.
(a) Haigh diagram for case 2
(b) Haigh diagram for case 5
Figure 8. Haigh diagram in each case
Lift Gate
Hinged Door
(a) Front door part slam test (b) L/Gate part slam test
Figure 9. Slam tester setting with door and L/Gate for cycle analysis

Endurance Analysis of Automotive Vehicle’s Door W/H System Using Finite Element Analysis 381
(a) Microscopic SEM analysis (b) X-Ray of the 7 cable bundle
Figure 10. Microscopic analysis by SEM (a) Microscopic SEM analysis
Table 3. Difference resistance and after high cycle test
Test 1 Test 2 Test 3 Test 4 Test 5 Test 6 Test 7 Test 8 Test 9 Test 10
Cycle 10,000 20,000 30,000 40,000 50,000 100,000 150,000 200,000 250,000 353,054
Sample 1 82.10 81.63 80.02 81.23 81.58 79.68 79.94 81.86 82.75 78.15
Sample 2 77.62 78.52 77.38 78.53 79.12 76.59 77.02 78.72 78.85 77.06
Sample 13 51.99 51.22 51.98 51.63 51.22 51.42 50.68 51.98 53.13 52.04
Sample 14 49.23 50.06 50.42 49.85 48.52 49.22 50.02 49.41 50.61 262.78
Sample 15 51.58 50.98 51.29 50.47 50.95 50.51 50.97 50.81 50.99 50.30
Table 4. Results of maximum stresses and endurance life cycles for the different cases (unit N/mm2)
Non linear Max. Stress 7.26
Case 1 (Depth 50mm) Endurance Cycle 487,000
Non linear Max. Stress 6.87
Case 2 (Depth 100mm) Endurance Cycle 518,000
Non linear Max. Stress 3.04
Cable No/Diameter
(7/0.32mm)
Case 3 (Depth 150mm) Endurance Cycle 600,000
Non linear Max. Stress 3.78
Case 4 (Depth 50mm) Endurance Cycle Infinite
Non linear Max. Stress 3.62
Case 5 (Depth 100mm) Endurance Cycle Infinite
Non linear Max. Stress 1.60
Cable No/ Diameter
(19/0.19mm)
Case 6 (Depth 150mm) Endurance Cycle Infinite
Through comparison above, the method of endurance
analysis and results of wire harness for the endurance of
flexible bending can secure the trust were shown in Table
5. The endurance life cycle is improved when the number
of cables with the same time as a big different depth is
changed.
The results obtained for the 6 cases of the Table 4 and
Table 5 show that:
- The 19-wire bundle is more flexible than the 7-wire
bundle.
- The maximum stress level is higher in the 7-wire
bundle.
- The stress level is higher for the 50 mm depth cases
in Table 4.
The FE analysis results indicate that the results are
well within the design standards. By adopting FE analy-
sis using ABAQUS and FEMFAT, it not only saves time,
money & slam testing but also guides the product engin-
eer for further improvement and modification of the W/H
system. The biggest challenges of such analyses are:

Endurance Analysis of Automotive Vehicle’s Door W/H System Using Finite Element Analysis 382
Table 5. Compare with slam test results and endurance analysis
Evaluation No of cable /Diameter Standard FE Analysis Result Test Result
7/0.32mm 100,000 487,000 353,054
Endurance Life Cycle
(Depth 50mm) 19/0.19mm 100,000 Infinite life Infinite life
FE modeling of the wiring hardness with analytical rigid
surfaces and dealing with convergence issues due to
large deformation of the elements. From this research to
improve the endurance life of W/H required for the life
cycle design, analysis and testing for the integration of
these technologies and secure source technology to de-
rive prototype, the following useful results were obtained.
The slam tester, designed and built by the vehicle’s test
was able to reduce the time and cost. The endurance life
cycle how to establish durable, and is designed to help
improve productivity, and to be tested. Through com-
parison of the test results and analysis, a vehicle’s W/H
of the results for the endurance can secure the trust wires,
depth due to the number of design guidelines to provide
for the endurance life efficiency.
5. Acknowledgments
This work was supported by the Korea Research Founda-
tion Grant funded by the Korean Government (MOE-
HRD) (KRF - 2007 - 521- D00057)
REFERENCES
[1] E. M. Bungo and C. Rausch, “Design requirements for:
metric-pack and global termina,” Packard Electric inter-
nal report, Warren, Ohio, 1990.
[2] P. Electric, “Environmentally protected connector sys-
tems,” Packard Electric internal report, Warren, Ohio,
1984.
[3] B. S. Kim and K. S. Lee, “Life prediction analysis of
wiring harness system for automotive vehicle,” Internal
report of Hoseo University, 2007.
[4] B. N. Lakshmi, G. William and S. A. Bhatia, “Non-linear
finite element analysis of typical wiring harness connec-
tor and terminal assembly using ABAQUS/CAE and
ABAQUS/Standard,” 2006 ABAQUS users’ conference,
Vol. 1, pp. 345–357, 2006.
[5] ABAQUS User's Manual Ver. 6.6, Dausault Systems Inc.,
2007.
[6] ABAQUS Example Problems Manual, Vol. 1, 6.2(ed.),
2007.
[7] K. Miller, G. Joldes, D. Lance and A. Wittek, “Total La-
grangian explicit dynamics finite element algorithm for
computing soft tissue deformation,” Communications in
numerical methods in engineering, Vol. 23, No. 2, pp.
121–134, 2007.
[8] G. Lingtian, L. Kaishin and L. Ying, “A meshless method
for stress-wave propagation in anisotropic and cracked
media,” International Journal of Engineering Science, Vol.
45, No. 2–8, pp. 601–616, 2007.
[9] G. Benjamin, I. Andrew and K. Peter, “Sensitivity analy-
sis of real-time systems,” International Journal of Com-
puter Science, Vol. 3, No. 1, pp. 6–13, 2008.
[10] K. Park, B. S. Kim, H. J. Lim and all, “Performance im-
provement in internally finned tube by shape optimiza-
tion,” International Journal of Applied Science, Engi-
neering and Technology, Vol. 4, No. 3, 2007.
[11] M. Fermer and H. Svensson, “Industrial experiences of
FE-based fatigue life predictions of welded automotive
structures,” Fatigue & Fracture of Engineering Materials
and Structures, Vol. 24, No. 7, pp. 489–500, 2001.
[12] W. Aichberger, H. Riener and H. Dannbauer, “Regarding
influences of production processes on material parameters
in Fatigue Life Prediction,” SAE 2007 World Congress,
Detroit, Vol. 26, 2007.
[13] C. Gaier, K. Kose, H. Hebisch and G. Pramhas, “Cou-
pling forming simulation and fatigue life prediction of
vehicle components,” NAFEMS 2005 Int. conference,
Malta, 2005.
[14] C. Halászi, C. Gaier and H. Dannbauer, “Fatigue life
prediction of thermo-machanically loaded engine com-
ponents,” 11th European automotive congress, Budapest,
2007.
[15] FEMFAT User's Manual Ver. 4.6, MAGNA Prowetrain
Inc., 2007.