Technology and Investment
Vol.1 No.2(2010), Article ID:1766,5 pages DOI:10.4236/ti.2010.12018
An Exploration of the R & D Value beyond the Generally Accepted Accouting Principles
Department of Finance and Banking, Lunghwa University of Science and Technology, Taoyuan, Taiwan, China
E-mail: 93441007@cc.ncu.edu.tw
Received October 28, 2009; revised February 1, 2010; accepted February 3, 2010
Keywords: real R & D option, Poisson event, exponential decay, GAAP
Abstract
This paper utilized the real R & D option theory especial the Bellalah [1] information cost model as the discussion base for the exploration of R & D value. We extended Bellalah’s model as to add the factors of Poisson event and exponential decay to approximate the reality; we calculated the derivative value of R & D investment and relaxed the Generally Accepted Accounting Principles (GAAP) as to deem the accumulated R & D investment the capital owned by a firm and to evaluate it as well. The empirical results enlightened us: our modified model meet with reality better than the original model; the derivative R & D value have explanatory power to the equity behavior especial the risk magnitude proxied by β and lastly, to entirely expense the R & D investment could be problematic since R & D investment own the property of capital.
1. Introduction
Merton asserted the importance of information cost and documented that an investor shall demand higher stock return if higher information cost is expensed [2]. Following the context of Merton, Bellalah [1,3] incorporated the information cost factor in valuing both options and R & D. However, in Bellalah’s setting only the factors influencing R & D’s market value were considered. The truth is that R & D value will depreciate while time elapses; its value could also be vanished overnight because of any unexpected evolution. These facts imply some other exogenous factors which influence the R & D’s payoff deserve to be comprehended. This study attempts to modify Bellalah’s ROM as to incorporate factors like exponential decay (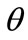 ) and Poisson event (
) and Poisson event (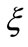 ) into consideration.
) into consideration.
There are three types of information cost defined including the average cost prevailed in market ( ), the cost affiliated with R & D options (
), the cost affiliated with R & D options ( ) and the cost affiliated with R&D yield’s price (
) and the cost affiliated with R&D yield’s price ( ). The disposal in Bellalah [1,3] may have caused two issues: first, the individual effect of information costs was unknown and, secondly, the reason of why the
). The disposal in Bellalah [1,3] may have caused two issues: first, the individual effect of information costs was unknown and, secondly, the reason of why the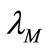 ,
, 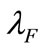 and
and 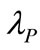 were set to be 4% for example was unknown. For the level of information cost, Bellalah stressed the hardness in defining it and proposed an alternative as to find proxies from derivates markets; though this idea was not taken eventually. We are going to observe the individual effect of information costs; we are also going to actualize Bellalah’s proposal to see what the real level of information cost could be.
were set to be 4% for example was unknown. For the level of information cost, Bellalah stressed the hardness in defining it and proposed an alternative as to find proxies from derivates markets; though this idea was not taken eventually. We are going to observe the individual effect of information costs; we are also going to actualize Bellalah’s proposal to see what the real level of information cost could be.
2. Re-Modeling
The factors of exponential decay 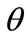 and Poisson event
and Poisson event 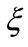 are going to be considered.
are going to be considered. 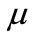 means the required rate of return which is the sum of expected capital gain
means the required rate of return which is the sum of expected capital gain  and dividend
and dividend . While exponential decay and Poisson event are jointly considered, the project value can be:
. While exponential decay and Poisson event are jointly considered, the project value can be:
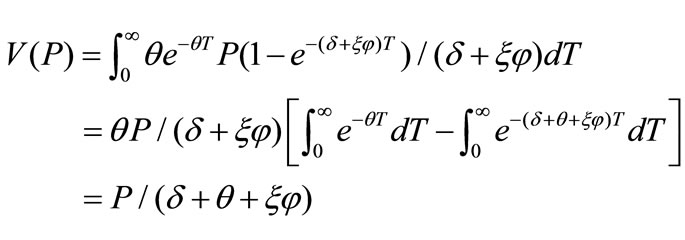 (1)
(1)
Through (1), a spiky event like  and
and  can be smoothened as an additional discount factor in the denominator.
can be smoothened as an additional discount factor in the denominator.
According to ROM, an R & D project value V can be seen as a combination of investment I and option value F therefore V(P) = I + F(P). We may utilize a portfolio  as to long one unit of option and to short
as to long one unit of option and to short  units output with price
units output with price  and let its payoff be:
and let its payoff be:
 (2)
(2)
From (2) we can derive a corresponding Bellman equation:
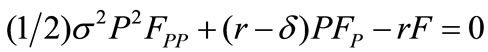 (3)
(3)
In (3), we set 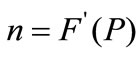 to eliminate the disturbance term
to eliminate the disturbance term . (3) is a Partial Differential Equation (PDE) and we can solve F by either analytical, if it has a close form solution, or numerical way. When the exponential decay, Poisson event and information cost are jointly considered, the Bellman equation becomes:
. (3) is a Partial Differential Equation (PDE) and we can solve F by either analytical, if it has a close form solution, or numerical way. When the exponential decay, Poisson event and information cost are jointly considered, the Bellman equation becomes:
 (4)
(4)
F solved from (4) is the value of a simple option and we denote it F1 in latter expressions.
We further consider a complex situation as to let the option compound with succeeding replacement options. P* means a threshold which is optimal to exercise the R & D project. When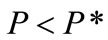 , the value of the compound option over next interval is:
, the value of the compound option over next interval is:
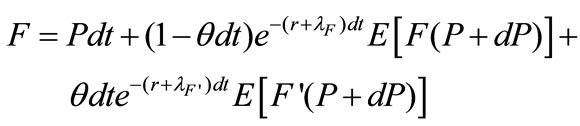 (5)
(5)
This means an installed investment could either survive with probability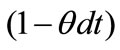 or die with probability
or die with probability  in next short interval. when
in next short interval. when , (5) can be expanded as:
, (5) can be expanded as:
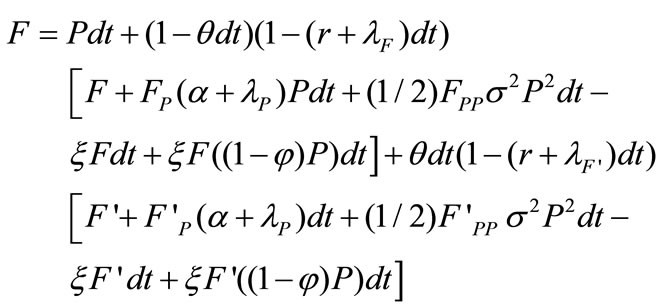
when , (5) can be expanded as:
, (5) can be expanded as:

The respective Bellman equation becomes:
 (6)
(6)
 (7)
(7)
Be noted that (6) and (7) will meet tangentially on P*. F solved from (6) and (7) is the value of a compound option and we denote it F2 in latter expressions.
3. Simulations
To illustrate the F1 and F2, we shall exploit an industrial case as the background to keep the simulations ‘virtual’. The ‘Local Area Network’ (LAN) industry in Taiwan was selected due to its high R & D orientation. The LAN industry in Taiwan is eye-catching referring to its annual global share 76.5%, 53%, 90.9% and 84% on NIC, Hub / Switch, SOHO router and WLAN (wireless LAN). We focused on the listed LAN companies and collect their financial and stock parameters from both Taiwan Economic Journal (TEJ) and the website of Taiwan Stock Exchange Corporation (TSEC). Sample period is from January 1st, 1999 to March 31st, 2006.
We set the parameters ,
, 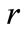 ,
, 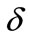 to equal the practical level and let
to equal the practical level and let ,
,  and
and 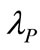 innovate in following simulations.
innovate in following simulations.
Figures 1 and 2 demonstrate the F1 and F2 value plane under influence of 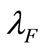 and
and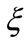 . Figures 3 and 4 demonstrate an additional influence caused by
. Figures 3 and 4 demonstrate an additional influence caused by . In Figure 1, the back (right) plane exhibits F1 which moves with information cost
. In Figure 1, the back (right) plane exhibits F1 which moves with information cost 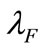 while keeping
while keeping 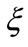 fixed; the front (left) plane exhibits F1 which moves with information cost
fixed; the front (left) plane exhibits F1 which moves with information cost 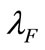 and Poisson event
and Poisson event  simultaneously. As shown, the plane will mainly incline toward
simultaneously. As shown, the plane will mainly incline toward  axis if
axis if
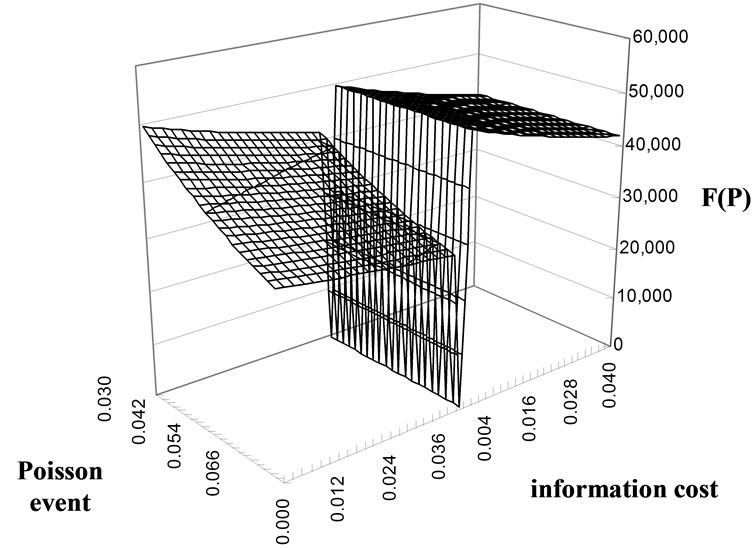
Figure 1. Value plane of F1.
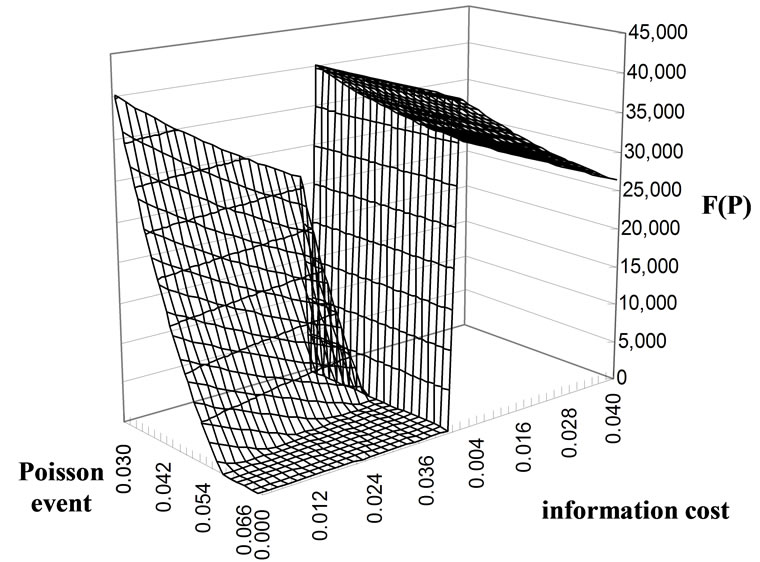
Figure 2. Value plane of F2.
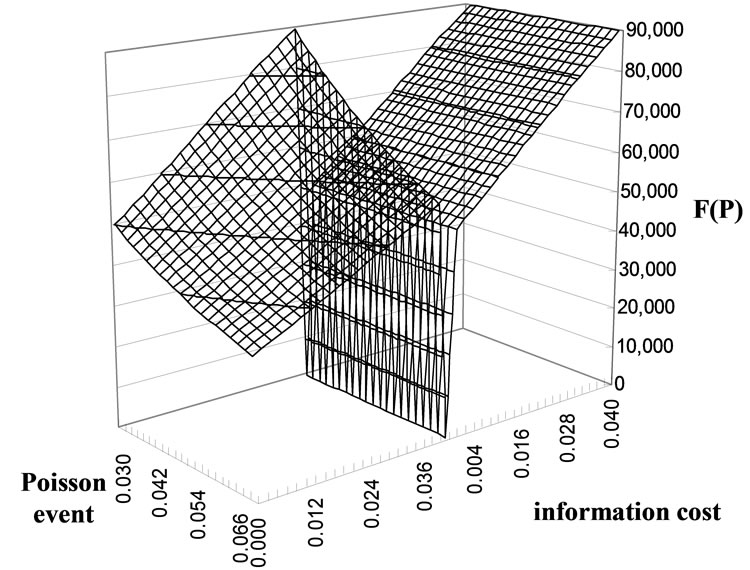
Figure 3. Value plane of F1 ( moves from 0 to 4%).
moves from 0 to 4%).
 is considered. This expounds that
is considered. This expounds that 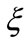 is a more influential factor; the scenario of Figure 2 is similar also. In Figures 3 and 4, we let the
is a more influential factor; the scenario of Figure 2 is similar also. In Figures 3 and 4, we let the 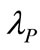 innovate with
innovate with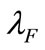 , which makes the plane toward information cost axis becoming a positive slope. The result implies that the appreciation of
, which makes the plane toward information cost axis becoming a positive slope. The result implies that the appreciation of 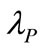 will raise the option value and partly cancel the influence of
will raise the option value and partly cancel the influence of . The value depreciation caused by
. The value depreciation caused by 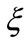 can somehow be alleviated by the raise of
can somehow be alleviated by the raise of 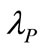 but not much;
but not much; 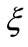 is still the major strength to domain the plane. Situations are similar if let the
is still the major strength to domain the plane. Situations are similar if let the 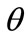 join
join
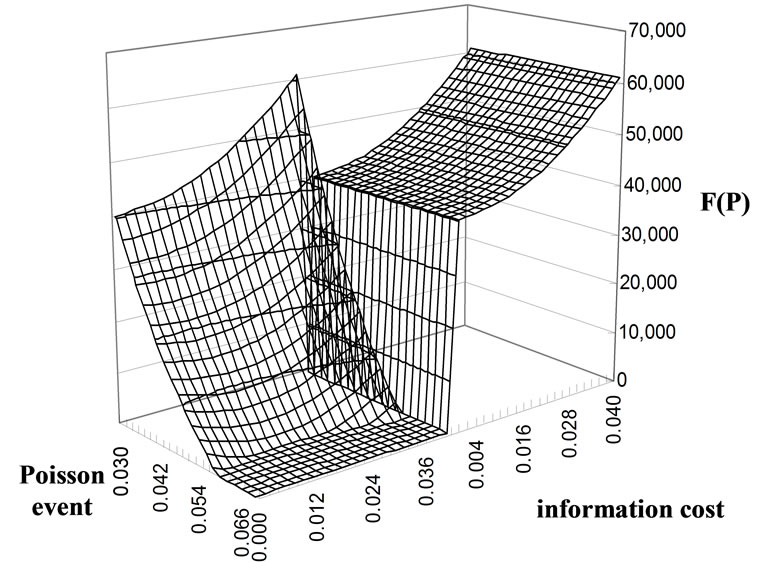
Figure 4. Value plane of F2 ( moves from 0 to 4%).
moves from 0 to 4%).
except the influence of 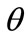 is minor than
is minor than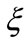 . The simulations elucidate two things: first, the incorporation of exogenous factors which influence to R & D’s payoff should be important since the new factors outweighs the information cost and, secondly, spending
. The simulations elucidate two things: first, the incorporation of exogenous factors which influence to R & D’s payoff should be important since the new factors outweighs the information cost and, secondly, spending 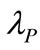 will improve the stochastic control on price thus a positive relationship with option value was observed.
will improve the stochastic control on price thus a positive relationship with option value was observed.
4. An Exploration to the Level of Information Cost
Bellalah stressed that the magnitude of information cost is hard to define and proposed an alternative as to collect proxies from derivates markets [3]. We are going to actualize Bellalah’s idea to find these proxies. The plausibility of proxies will be tested by the regression analysis:
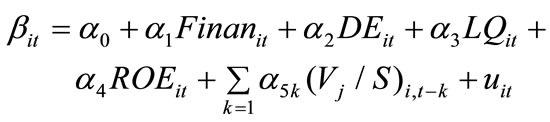 (8)
(8)
i denotes the sample companies,  ,
, 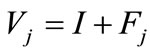 , t denotes time.
, t denotes time.  means the beta coefficient belonging to CAPMi which represents the risk level. Since the higher R&D investment will incur a higher company’s risk [4,5], we take
means the beta coefficient belonging to CAPMi which represents the risk level. Since the higher R&D investment will incur a higher company’s risk [4,5], we take  as a dependent variable to be regressed and a positive coefficient of
as a dependent variable to be regressed and a positive coefficient of  is expected. The financial leverage (Finan), debt-equity ratio (DE), liquidity (LQ) and profitability (ROE) are comprehended as control variables. We let V be divided by contemporaneous sales to eliminate the idiosyncratic scale effect. (8) implies that
is expected. The financial leverage (Finan), debt-equity ratio (DE), liquidity (LQ) and profitability (ROE) are comprehended as control variables. We let V be divided by contemporaneous sales to eliminate the idiosyncratic scale effect. (8) implies that 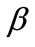 is a function of multi-period R&D value. Be noted the multicollinearity could happen on
is a function of multi-period R&D value. Be noted the multicollinearity could happen on 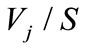 therefore a polynomial distributed lags (PDL) technique is exploited.1
therefore a polynomial distributed lags (PDL) technique is exploited.1
Before collecting the proxies of information costs, we need to clarify two issues including what the adequate proxy should be and how the proxy can be collected. For the first issue, we followed Amihud and Mendelson [6] who asserted that the bid-ask spread an adequate proxy of information cost; for the second issue, we followed the Chicago Board Options Exchange (CBOE) disciplines in estimating the volatility index (VIX).2 ,
, 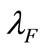 and
and 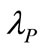 can be estimated by Taiwan weighted stock index (TAIEX), stock options and common stocks. Anyway, we utilized the data from Taiwan stock index options (TXO) for
can be estimated by Taiwan weighted stock index (TAIEX), stock options and common stocks. Anyway, we utilized the data from Taiwan stock index options (TXO) for  and Taiwan electronics options (TEO) for
and Taiwan electronics options (TEO) for  since there’s no TAIEX transactions and no individual stock options offered by sample companies. The proxies collected from markets are deemed the real level of information cost.
since there’s no TAIEX transactions and no individual stock options offered by sample companies. The proxies collected from markets are deemed the real level of information cost.
Table 1 shows the situation while . On Table 2 we start to consider the non-zero situation and let the cost be either Bellalah’s [3] or real level. The AdjR2 slightly changed between Tables 1 and 2 while letting the cost be the Bellalah’s level. The change becomes remarkable if let the cost be the “real”. Be noticed that the averaged
. On Table 2 we start to consider the non-zero situation and let the cost be either Bellalah’s [3] or real level. The AdjR2 slightly changed between Tables 1 and 2 while letting the cost be the Bellalah’s level. The change becomes remarkable if let the cost be the “real”. Be noticed that the averaged ,
, 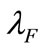 and
and 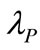 are 2.14%, 23.24% and 0.23%; which is much different with Bellalah’s setting.
are 2.14%, 23.24% and 0.23%; which is much different with Bellalah’s setting.
5. Conclusions
The Bellalah’s [1,3] model can though depict the change of R & D’s market value due to the spillover effect of information collecting, it cannot figure the change of R & D’s payoff due to the competitor’s activity. This makes Bellalah’s model deviating to the reality. We made extension to Bellalah’s models as to incorporate exogenous factors including exponential decay  and Poisson event
and Poisson event  for compensation on aforesaid deficiency.
for compensation on aforesaid deficiency.
The influence of information cost onto R & D value is roughly half to exponential decay  and one third to Poisson event
and one third to Poisson event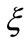 , which tells the new added factors outweighs the information cost as well as support our modeling extension. Bellalah [1,3] did not observe the information cost individually but a lump-sum effect instead; we made an individual survey and found that the information cost affiliated with price
, which tells the new added factors outweighs the information cost as well as support our modeling extension. Bellalah [1,3] did not observe the information cost individually but a lump-sum effect instead; we made an individual survey and found that the information cost affiliated with price 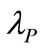 moves conversely from the others. This finding implies that the cost in pursuing a more adequate price will boost the R & D value, vice versa.
moves conversely from the others. This finding implies that the cost in pursuing a more adequate price will boost the R & D value, vice versa.
Bellalah [3] commented that the information cost is hard to define and, therefore, suggested to find proxies from the derivates markets. However, such an idea was not taken eventually but only artificial numbers instead in Bellalah’s simulations. We actualized Bellalah’s idea and propose a working frame as to exploit the ways of

Table 1. The explanatory power of different R & D value approaches.

Table 2. The explanatory power influenced by information cost.
volatility indices estimation. The average level of the proxies of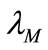 ,
, 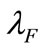 and
and  are 2.14%, 23.24% and 0.23%. The new level is much different than the conventional knowledge and seems more plausible since it brings better predictability on
are 2.14%, 23.24% and 0.23%. The new level is much different than the conventional knowledge and seems more plausible since it brings better predictability on , this helps investors being more prudent because he knows better the risk level what have borne by portfolio.
, this helps investors being more prudent because he knows better the risk level what have borne by portfolio.
6. References
[1] M. Bellalah, “Valuation of Futures and Commodity Options with Information Costs,” The Journal of Futures and Markets, Vol. 19, 1999a, pp. 645-664.
[2] R. C. Merton, “A Simple Model of Capital Market Equilibrium with Incomplete Information,” The Journal of Finance, Vol. 42, No. 3, 1987, pp. 483-510.
[3] M. Bellalah, “On Irreversibility, Sunk Costs and Investment Under Incomplete Information,” In: Paxson, D. A. Ed., Real R & D Options, Butterworth Heinemann, Burlington, 2003b.
[4] F. Black and M. Scholes, “The Pricing of Options and Corporate Liabilities,” Journal of Political Econometrics, Vol. 81, No. 3, 1973, pp. 637-654.
[5] Y. K. Ho, Z. Y. Xu and C. M. Yap, “R & D Investment and Systematic Risk,” Accounting and Finance, Vol. 44, No. 3, 2004, pp. 393-418.
[6] Y. Amihud and H. Mendelson, “The Effects of Beta, Bid-Ask Spread, Residual Risk, and Size on Stock Returns,” The Journal of Finance, Vol. 44, No. 2, 1989, pp. 478- 486.
[7] R. E. Whaley, “The Investor Fear Gauge,” Journal of Portfolio Management, Vol. 26, No. 3, 2000, pp. 12-17.
NOTES
1We set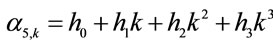 ,
, 
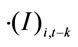
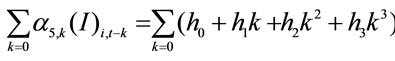 ,
, 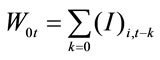 ,
,  ,
,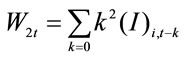 , and
, and . The degree is set to be three since the significance level of
. The degree is set to be three since the significance level of 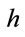 remarkably descends from degree of four.
remarkably descends from degree of four.
2CBOE demands the contract series of “near-the-money”, “nearby” and “second-nearby” being applied for VIX estimation. For the contracts with days less than six to the expiration, CBOE demands the contract series of second-nearby and third-nearby being applied to avoid the possible fluctuation on price [7].

