Journal of Modern Physics
Vol.06 No.04(2015), Article ID:55000,13 pages
10.4236/jmp.2015.64047
A Formulation of Quantum Theory Based on Two Physical Principles
R. T. Deck
Department of Physics, University of Toledo, Toledo, USA
Email: rtd@physics.utoledo.edu
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 November 2014; accepted 21 March 2015; published 25 March 2015
ABSTRACT
We demonstrate two points: 1) the formalism of quantum mechanics can be understood simply as a structure for the expression of the physical notion that not all observables can have values simultaneously; 2) the specific uncertainty relations can be derived (rigorously) by combination of the invariance principle with a general uncertainty relation based only on the existence of unspecified pairs of conjugate observables. For this purpose, we present a formulation of quantum mechanics based strictly on the invariance principle and a “weak” statement of the uncertainty principle that asserts only the existence of incompatible (conjugate) observables without specifying which observables are incompatible. We go on to show that the invariance principle can be used to develop the equations of motion of the theory, including the Klein-Gordon and Schrodinger equations.
Keywords:
Uncertainty Principle, Invariance Principle, Klein-Gordon Equation, Schrodinger Equation

1. Introduction
While the famous uncertainty relation  first stated by Werner Heisenberg is well known, few know that this relation can be derived from the translational symmetry of space on the basis of a much more general uncertainty relation. The purpose here is to indicate that the entire structure of the quantum theory and its most basic content derive from only two physical principles, which can be referred to as the principle of uncertainty and the principle of invariance (stated below). A more complete demonstration can be found in [1] .
first stated by Werner Heisenberg is well known, few know that this relation can be derived from the translational symmetry of space on the basis of a much more general uncertainty relation. The purpose here is to indicate that the entire structure of the quantum theory and its most basic content derive from only two physical principles, which can be referred to as the principle of uncertainty and the principle of invariance (stated below). A more complete demonstration can be found in [1] .
Here, by the principle of uncertainty is meant simply the notion that there are sets of incompatible observables that cannot have precise values simultaneously. More particularly, the principle expresses the fact that there exist certain pairs of “conjugate observables”, a and b, the simultaneous values of which have irreducible intrinsic uncertainties Da and Db that satisfy an inequality of the form
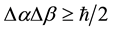 (1)
(1)
where  is a fundamental constant of nature (equal to Planck’s constant h over 2p). By the principle of invariance is meant the notion that the laws of physics should have the same form in all physically equivalent coordinate frames. It is remarkable that the entire content of ordinary (single particle) quantum mechanics can be reduced to the above two principles with no stronger statement of the principle of uncertainty than is given above. In particular, although the principle as stated asserts only the existence of pairs of observables without defining which observables are in fact conjugate, specific pairs of conjugate observables can be deduced from the general principle in the form above by combining it with the principle of invariance. More precisely, given the assumption of the existence of conjugate observables satisfying the “uncertainty relation” written above, without specifying the nature of these observables, it can be shown (in the manner indicated here) that the invariance principle requires certain pairs of observables to satisfy such a relation, and that these pairs of observables are those found in nature.
is a fundamental constant of nature (equal to Planck’s constant h over 2p). By the principle of invariance is meant the notion that the laws of physics should have the same form in all physically equivalent coordinate frames. It is remarkable that the entire content of ordinary (single particle) quantum mechanics can be reduced to the above two principles with no stronger statement of the principle of uncertainty than is given above. In particular, although the principle as stated asserts only the existence of pairs of observables without defining which observables are in fact conjugate, specific pairs of conjugate observables can be deduced from the general principle in the form above by combining it with the principle of invariance. More precisely, given the assumption of the existence of conjugate observables satisfying the “uncertainty relation” written above, without specifying the nature of these observables, it can be shown (in the manner indicated here) that the invariance principle requires certain pairs of observables to satisfy such a relation, and that these pairs of observables are those found in nature.
Although the manner in which quantum theory is developed is hallowed by tradition, and readers steeped in a view of the subject they have come to terms with may not be open to an alternative interpretation, it is the contention here that the development outlined below simplifies the interpretation of the theory, and therefore deserves a place in the literature. Specifically, it addresses the first question that a student of quantum mechanics should have, namely, the question why the formalism of the theory must be changed from the formalism of classical physics in which observables are represented by mathematical variables. The historical approach to quantum mechanics provides a somewhat complicated answer to this question, whereas it is made evident here that the simple answer is the existence of pairs of observables that cannot have precise values simultaneously. Although the importance of the principles of uncertainty and invariance in quantum theory is well recognized, we are unaware of either a treatise on the subject that develops the theory strictly on the basis of these two principles or a place in the literature where the two points in the abstract are stated. Instead, the theory is either presented following the line of its historical development on the basis of the asserted wave nature of matter [2] , or developed (in more “rigorous” presentations) as the consequence of postulated axioms (the number and form of which can vary in different formulations) [3] [4] . In the more rigorous developments based on postulated axioms, because certain axioms represent purely mathematical statements relating to the structure of the formalism while other axioms have some limited physical content, it is difficult to separate the physical content from the mathematical formalism, and therefore difficult to determine what the basic physical content of the theory is. Given that the extent to which mathematics describes physical phenomena is remarkable, there should nevertheless exist a distinction between the mathematics that quantitatively expresses the laws governing physical phenomena and the physical principles that underlie those laws.
In the traditional developments of the quantum theory, the uncertainty principle is sometimes derived as a consequence of what are made to appear more basic or at least equally basic notions, and the fundamental nature of this principle is therefore obscured. In contrast, it is contended here that the uncertainty principle by itself is sufficient to both justify the entire mathematical formalism underlying the theory and to allow for a derivation of the quantum mechanical equations that result from it. Moreover, it is shown here that the development of the theory based on the uncertainty principle makes evident the fact that the quantum mechanical formalism proves useful only because it allows for a simple quantitative expression of the notion of incompatible observables. It is significant that the few rules and definitions used to define the formalism are no more numerous than those assumed in any formulation of the theory. That the resulting formalism is self consistent and leads to no physical content other than that embedded into it by the notions of uncertainty and invariance is demonstrated in detail in [1] .
To make the points above, certain well known equations are restated in Section II and III.A for the purpose of showing that the content of these equations is that contained in Equation (1). Since it is understood that content is added to the theory through the invariance principle, Section III.B is intended to emphasize exactly how its content enters the formalism and to demonstrate that the principle leads to the existence of explicit pairs of conjugate observables. Specifically, it is shown to be a consequence of Equation (1) and the definition of the generator of an infinitesimal displacement, that the observable associated with the generator of the displacement is conjugate to a coordinate observable and has all the properties of the linear momentum1.
2. Development of Formalism
To construct a quantitative theory to describe physical phenomena it is necessary to make use of some mathematical formalism in terms of which physical principles can be expressed so as to lead to quantitative relations between observables. Because the principle of uncertainty is entirely restrictive in its content, its role is primarily to restrict the mathematical formalism in terms of which the physical theory can be expressed. In principle, the nature of the formalism is arbitrary provided it allows for proper expression of the adopted principles and provided the axioms underlying it are consistent in a rigorous mathematical sense. The well known elements of the quantum formalism are reviewed here only to emphasize that they provide a remarkably simple basis for expression of the single notion that not all observables have exact values at the same time. In a classical theory, the formalism consists of relations between symbols representing the values of observables, and the symbols of the formalism therefore have the properties of mathematical variables. On the other hand, in a quantum theory that takes account of the principle of uncertainty, the formalism of the classical theory must be altered precisely because all observables do not have exact values in a given state of a physical system. Specifically, the formalism must be altered so as to prevent the assignment of precise values to observables that do not have precise values simultaneously. This necessary alteration of the formalism is accomplished most simply by expressing the relations between observables as operator relations in which observables are represented by operators (denoted O) that act on a symbol called a ket (denoted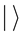 ) which serves to keep track of the accuracy to which values can be assigned to particular observables in a given state. From this point of view the ket can be defined as a listing of the observables that specify a given state, along with the mean values of, and uncertainties in, those observables.
) which serves to keep track of the accuracy to which values can be assigned to particular observables in a given state. From this point of view the ket can be defined as a listing of the observables that specify a given state, along with the mean values of, and uncertainties in, those observables.
Since the uncertainty principle disallows the possibility that all observables can have precise values simultaneously, it is necessary to distinguish between states in which certain observables have precise values and states in which all observables have only imprecise values. A state in which certain observables have precise values is referred to as an eigenstate of those observables, and the ket that represents it is referred to as an “eigenket”.The eigenket represents a listing of the observables and the values of those observables that specify the eigenstate.
In the development of the formalism it is found sufficient to define only one rule of operation for an operator acting on a ket, namely. the rule that determines the result of an operator corresponding to an observable acting on an eigenket of that observable. Given an observable a, and an associated operator 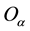 and eigenket
and eigenket , this one rule of operation is defined by the equation
, this one rule of operation is defined by the equation
 (2)
(2)
where 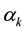 denotes the eigenvalue of a in the eigenstate represented by
denotes the eigenvalue of a in the eigenstate represented by . The sufficiency of this rule follows from the fact that the formulation of the principle of uncertainty results in a prescription whereby any ket is expressible in terms of the eigenkets of any operator relating to the same degrees of freedom; by use of which any operator acting on any ket is expressible in terms of that operator acting on its eigenkets, the result of which is determined by the above rule. More importantly, the above rule has the effect of reducing the quantum formalism to a classical formalism whenever the principle of uncertainty is ignorable. In particular, by use of the above rule, the quantum formalism is such that whenever all operators in an operator equation correspond to observables that can have precise values simultaneously, each operator in the equation can be replaced by a variable representing its eigenvalue; in which case the kets can be canceled from each term and the operator equation can be reduced to a “classical equation”.
. The sufficiency of this rule follows from the fact that the formulation of the principle of uncertainty results in a prescription whereby any ket is expressible in terms of the eigenkets of any operator relating to the same degrees of freedom; by use of which any operator acting on any ket is expressible in terms of that operator acting on its eigenkets, the result of which is determined by the above rule. More importantly, the above rule has the effect of reducing the quantum formalism to a classical formalism whenever the principle of uncertainty is ignorable. In particular, by use of the above rule, the quantum formalism is such that whenever all operators in an operator equation correspond to observables that can have precise values simultaneously, each operator in the equation can be replaced by a variable representing its eigenvalue; in which case the kets can be canceled from each term and the operator equation can be reduced to a “classical equation”.
To connect the formalism to the results of physical measurements it is necessary to connect the elements of the formalism to real numbers. This is done by introducing quantities “conjugate” to kets, known as bras (and denoted ), and by defining the “expectation value” of an observable. The resulting equations are well known [5] . For every ket
), and by defining the “expectation value” of an observable. The resulting equations are well known [5] . For every ket 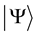 a conjugate bra
a conjugate bra 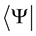 is defined such that its product with
is defined such that its product with 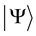 from the left is a positive real number, denoted by
from the left is a positive real number, denoted by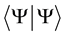 . Similarly, for every ket
. Similarly, for every ket 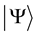 multiplied (on the left) by an operator O, a
multiplied (on the left) by an operator O, a
conjugate quantity written 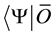 is defined such that its product with
is defined such that its product with 
number (denoted





The rule in Equation (3) is consistent with the basic rule of operation (2) whereby the expectation value of a in an eigenstate of a is reduced to its eigenvalue. To define all potential operations within the formalism it is necessary to include the rule of operation of an operator 
operator. The rule is expressed by the equation
with real eigenvalues must be “self-adjoint” so as to satisfy the equation

The definition of the “value” of an observable in Equation (3) makes possible a quantitative definition of the uncertainty in the value of an observable. The uncertainty is defined in analogy with the conventional uncertainty in the result of measurements of an observable a, given by the “root-mean-square-deviation” of the meas-
ured values from the mean, written

rate measurements. Because the expectation value plays the role of the average value in the quantum formalism, we define the quantum mechanical uncertainty Da by the equality

where 
3. Incorporation of Principles
3.1. Uncertainty Principle
It remains to express the principle of uncertainty quantitatively in the formalism. This is accomplished by defining a “superposition relation” for kets, which results in certain commutation relations for operators. Since the rules of the formalism given above determine only the operation of an operator on an eigenket of that operator, there exists arbitrariness in the formalism relating to the operation of an operator on a ket that is not an eigenket. In particular, it remains to prescribe the operation of an operator 

Dak and Dbk. The operation of 


A prescription for the operation of 

(and its counterpoint with a and b interchanged). Below, for simplicity, all kets are assumed to be normalized to unity and the eigenvalues aj are taken to be discrete and to lie in the interval between 


The extent to which superposition relations of the above form provide a proper expression of the principle of uncertainty must depend on the extent to which the equations resulting from the relations can be interpreted in a manner consistent with the principle. In particular, use of the relation (6) in the defining equation (3) must result in an expectation value of a consistent with the uncertainty in a. To compute this expectation value in the state represented by the ket 



the fact that its product with 



Here the normalization of all kets to unity guarantees the equality

Equations (7) and (8) show the expectation value of a in the state represented by the ket 



The prescription for representation of the ket 




Given the form and interpretation of the superposition relation (6), inclusion of terms in the superposition relation with zero coefficients (corresponding to zero probabilities) then allows summations over 
A more quantitative expression of the uncertainty principle in the formalism is obtained through an equation for the value of the “commutator” of a pair of operators corresponding to conjugate observables. The equation can be developed from the definition of the uncertainty in an observable α in Equation (5) together with the expression for the expectation value in Equation (3).In particular, by multiplying together the uncertainties in observables α and b as expressed by Equation (5), and use of the definition of the expectation value in Equation (3), an expression for the product 

where the bracket 




consistent with the commutability of operators in the limit of zero


The relations (11) combined with Equation (2) make possible a re-expression of the operator Equation (10) as an ordinary equation connecting functions of α and b. The result is obtained by multiplication of Equation (10) on the left and right respectively by eigenbras and eigenkets of α to produce the relation

which Equations (2) and (11) (and choice of the “+” sign) reduce to the form

The extremely singular character of this last relation (for

then requires the quantity 

The equivalence can be reworked into a more general relation (and its adjoint) by expansion of an arbitrary ket 

The expansion makes it possible to rewrite Equation (14) as the more general relation

which (combined with the symmetry between α and b) serves to establish the well known prescriptions that define the result of an observable operator acting on a continuum eigenket or eigenbra of a conjugate observable


with the lack of complete symmetry between α and b a reflection of the particular choice of sign in the commutation relation of Equation (10).
The prescriptions (17), together with the rule (2), lead immediately to a differential equation for the bra-ket product 

which has the solution

where C is an arbitrary complex constant, independent of both 















The physical content of the formalism is increased by the addition of the principle of invariance. As an example of this, in the section below, the results obtained from this principle are derived in the simple case of invariance of the equations of the theory with respect to space translations. The results extracted from the invariance principle applied to the complete set of transformations in the Lorentz group are detailed in Reference [1] .
3.2. Invariance Principle
The recognition of the existence of equivalent space-time frames relative to which the equations of physics should have the same form represents the essential notion underlying the “physical principle of invariance”. The content of the principle is then contained in the assertions that define certain distinct frames to be equivalent. Here, for simplicity, we focus only on the asserted physical equivalence of coordinate frames connected to one another by either a shift in the coordinate origin or a rotation of the coordinate axes. In either case, the space coordinates of a system with respect to the initial frame will be labeled x, y, z, while the coordinates of the same system with respect to the “transformed frame” will be labeled

In the ket picture, a transformation between an unprimed and a primed coordinate frame is asserted to leave the operators unaltered,

but is defined to result in a change in the bras and kets that describe the system by way of the prescriptions

with the quantity 


where the change in the expectation value 



but to result in a change in the operators according to the relation

In this case the expectation values of physical observables transform as

where the change in 




Additional physical content is introduced into the definition of the transformation operators by the requirement of conservation of probability below. In the case of a linear transformation, this requirement restricts the transformation operator U to be unitary, as defined by the equation (see below),

in which case Equation (25) can be rewritten in the form
It is sufficient here to consider the case of continuous transformations that can be evolved from the identity operator I by a continuous sequence of transformations generated by infinitesimal variations in a parameter a. In this case, the transformation operator U can in general be represented as

where 


We focus here on a transformation between the physically equivalent frames of a closed system resulting from an infinitesimal translation of the coordinate origin by an amount 


where 

3.2.1. Ket Picture of Translation
Consider first the ket picture of the coordinate transformation in which the operator 

where the kets 










The result (32) combined with Equations (29), (30), and (31) is sufficient to determine the properties of the operator G, and in addition demonstrate that the observable associated with the related operator 

The derivation proceeds on the basis of well known steps. By use of Equations (29), (30), and (31) the primed frame quantities 


The functions of 







By substitution of Equations (34) into Equation (33) and the neglect of terms proportional to the square of 

which reduces to the result

The result is sufficient to establish that the observable 




the form of Equation (36), in terms of the operator


But, since Equation (16) derives from the commutation relation (10) that represents an expression of the uncertainty relation


which in turn implies that the observable


That the operator 






3.2.2. Operator Picture of Translation
Consider now the operator picture of the infinitesimal translation in which an operator 


By use of Equations (30) and (37) and the self-adjointness of the operator


The interest is in the connection between the operators corresponding to coordinate observables 


lues of the coordinate operators are required to be related by Equation (29). It follows that the coordinate operators in the primed and unprimed frames, 



from which it follows that the operator 

operator 
tion, which is valid when the operators in the equation act on any ket:

In particular, since the above connection between the operators 

tors act on the eigenkets

tion between the operators must be valid when the operators act on any ket on which they can act. But as a consequence of Equation (41), the operators 


and it follows from comparison of Equations (44) and (45) that the operators 


Here the operator 



by use of which Equation (46) can be reduced to an equality relating strictly to the degrees of freedom connected to the coordinate vector


It then follows from the fact that the derived commutation relation between the operators 
is identical to the commutation relation between operators associated with conjugate observables, that the observables 


The conclusion extracted from the operator picture of the coordinate translation is therefore the same as that deduced from the ket picture of the transformation (as it should be). In fact, because Equation (36)’ can be derived from Equation (46), the property of the operator 

Similarly, by considering the connections between coordinate frames related by a rotation of the coordinate axes rather than by a translation of the origin, an analysis parallel to the above demonstrates that the observable associated with the (properly defined) generator of an infinitesimal rotation about the k-th coordinate axis, 


with the operator associated with the observable 


It can be demonstrated that the observables associated with the generators of infinitesimal translations and rotations have in fact all the familiar properties of linear and angular momentum observables [1] . Specifically, the invariance principle requirement that the equations of motion of a closed system be unaltered by a translation or rotation demands that the generators of the transformations commute with the Hamiltonian and that their eigenvalues therefore be constants of the motion. In addition, it is shown below that the linear momentum observable is connected in the usual way to the energy observable, which itself can be associated with the generator of an infinitesimal translation of the origin of time. The overall conservation of linear momentum and energy can then be derived from the invariance principle requirement that the equations of motion of a closed system be invariant in form under translations of the origins of the space and time axes. The connection between the energy observable and the generator of a time translation also allows for a rigorous derivation of an energy-time uncertainty relation expressing the well known connection between the energy “width” and the lifetime of a state2 [1] [8] .
It is important that Equation (36)' in the form

where 


The covariance of the equations under the complete set of Lorentz transformations requires that the two equations be combinable into a four-vector equation. This can be guaranteed only under the condition that the operators 




But when an equation involves only simultaneous observables, the equation must be valid when the values of the observables are replaced by their corresponding operators acting on any ket 

Multiplication of Equation (55) on the left by a coordinate eigenbra 

which the notation

re-expresses as

An approximate equation for a free particle can be derived from this equation by solution of Equation (54) for the energy eigenvalue E in terms of a square root, and approximation of the square root in the case in which

The validity of Equations (58) and (59) is limited by the fact that the forms of the equations are altered by a phase change in the function





where 




with 



with
4. Summary and Conclusion
What is demonstrated here is that combination of the invariance principle with only a weak statement of the uncertainty principle that asserts only the existence of unspecified pairs of conjugate observables is sufficient to establish the existence of specific pairs of such observables, which in fact exhaust the complete set of known pairs of observables satisfying uncertainty relations of the form (1). It is shown in addition that the invariance principle, formulated within the quantum formalism, determines the forms of the basic “equations of motion” of the theory.
Acknowledgements
The author thanks Professor D. G. Ellis for useful comments relating to this paper.
References
- Deck, R.T. (2010) A Logical Development of Quantum Mechanics from Physical Principles. CreateSpace 2010.
- Eisberg, R. and Resnick, R. (1985) Quantum Physics. 2nd Edition, John Wiley & Sons, New York.
- Merzbacher, E. (1970) Quantum Mechanics. 2nd Edition, John Wiley & Sons, New York.
- Liboff, R.L. (1992) Introductory Quantum Mechanics. 2nd Edition, Addison-Wesley, New York, 66-80.
- Dirac, P.A.M. (1958) The Principles of Quantum Mechanics. 4th Edition, Clarenden Press, Oxford.
- Goswami, A. (1992) Quantum Mechanics. 2nd Edition, Wm.C. Brown Publishers, Dubuque.
- Deck, R.T. and Ozturk, N. (1994) Foundations of Physics Letters, 7, 419-436. http://dx.doi.org/10.1007/BF02189245
- Sposito, G. (1970) An Introduction to Quantum Physics. John Wiley & Sons, Inc., New York, 178.
NOTES
1What is emphasized is not the relationship between the generator of a displacement and the linear momentum, which is well known, but that the relationship follows from Equation (1) and the invariance principle.
2Because time needs to be interpreted as a parameter in the theory rather than an observable, the derivation and interpretation of the uncertainty relation connecting energy and time are very different from those developed here for the observables x and px.




