ABSTRACT

The well-known Schrdöinger equation is reasonably derived from the well-known diffusion equation. In the present study, the imaginary time is incorporated into the diffusion equation for understanding of the collision problem between two micro particles. It is revealed that the diffusivity corresponds to the angular momentum operator in quantum theory. The universal diffusivity expression, which is valid in an arbitrary material, will be useful for understanding of diffusion problems.

1. Introduction

For micro particles such as atoms or molecules in the homogeneous time and space of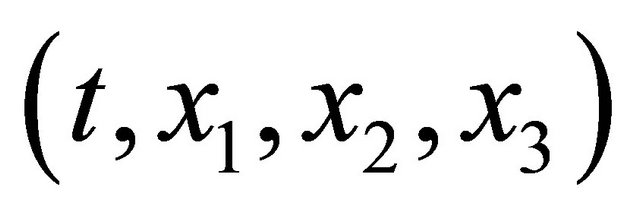, the macro behavior of their collective motions is presented by the well-known diffusion equation of

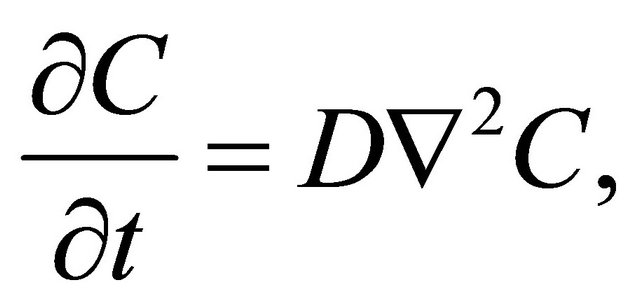(1)

where 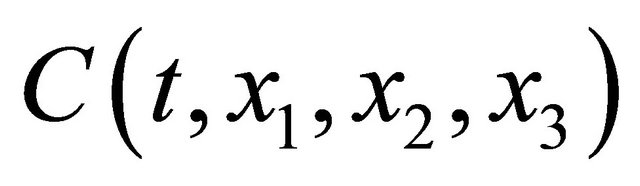is the concentration of them and

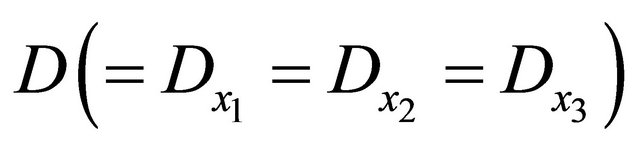the diffusivity when it does not depend on 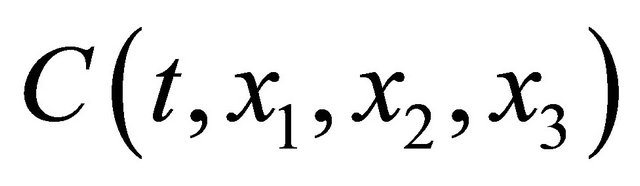[1].

The motion of a micro particle is presented by quantum mechanics and its behavior is investigated by using the Schrödinger equation of

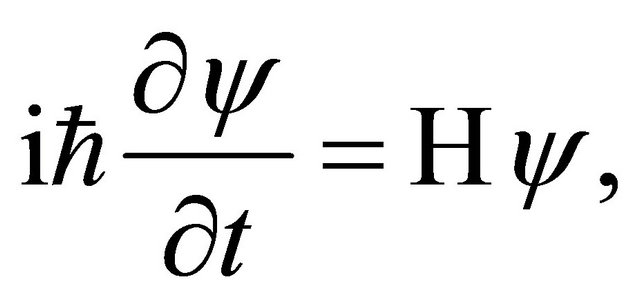(2)

where 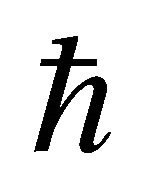is 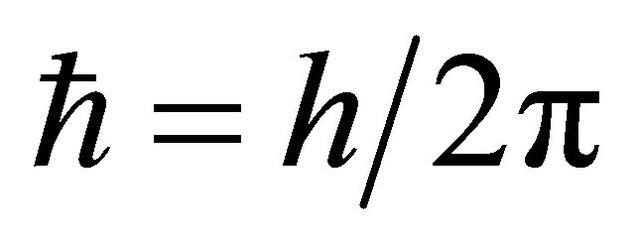using the Plank constant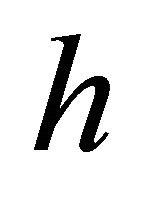, 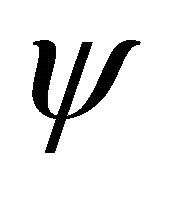the state vector and the Hamiltonian meaning the total energy in the given physical system [2]. In case of a free particle, it is given by

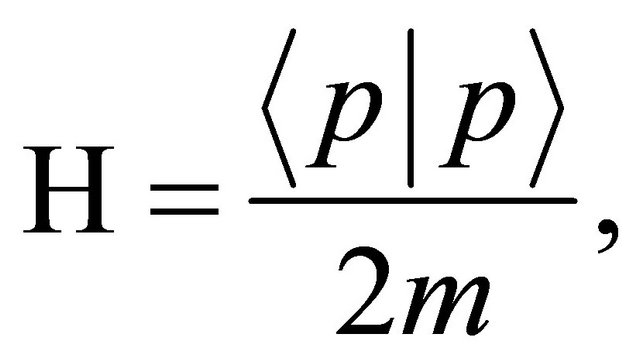(3)

where 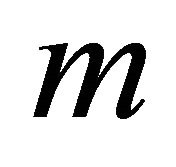is the particle mass and the momentum.

In the present study, the correlation between (1) and (2) was investigated. It was found that the Schrödinger equation (2) is reasonably derived from the diffusion equation (1) by means of using the imaginary time for (1). As a result, we revealed that the diffusivity 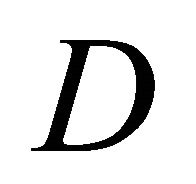in (1) corresponds to the angular momentum operator in quantum mechanics. The obtained new diffusivity will be useful for understanding of an elementary process of diffusion [3].

2. Necessity of Imaginary Time

The micro particle in a solid crystal jumps instantly to the nearest lattice site through an energy barrier when it obtains an activation energy caused by the thermal fluctuation. The micro particle in a fluid collides with another one via the movement of the averaged free path and the particle jumps to a neighbor site.

For a Brownian particle of mass m, the well-known Langevin equation is

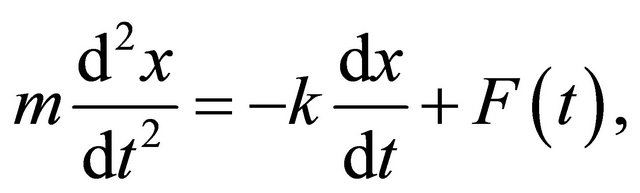(4)

where the velocity 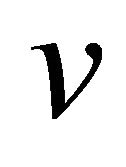and the viscosity resistance f are

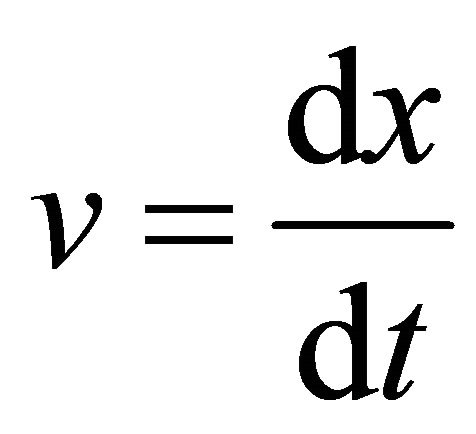and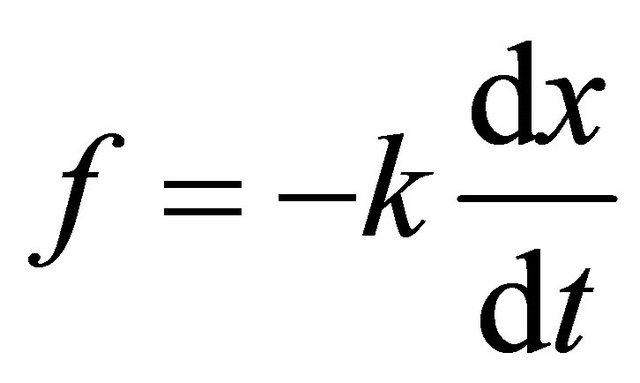, respectively [4]. In (4), the time-averaged value of external force satisfies

in a collision problem. Hereafter, we do not discuss 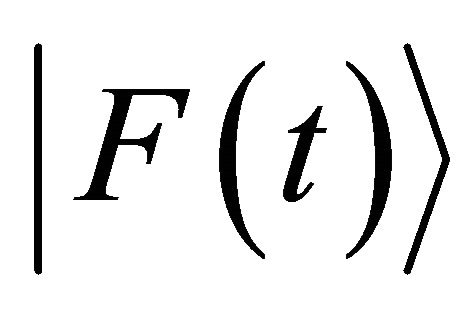but the acceleration in a collision problem between two micro particles. In the three dimensional space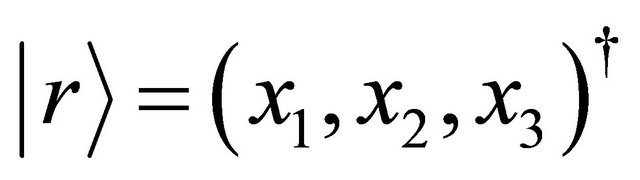, the acceleration is expressed as:

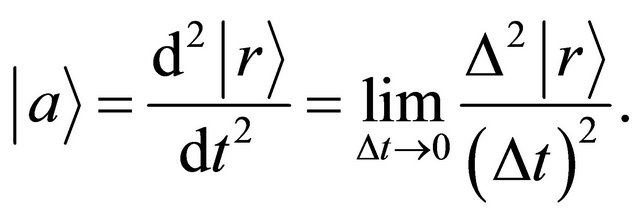(5)

Since the physical essence is still kept even if we consider the simplest collision problem of one dimensional case, we thus investigate a perfect elastic collision problem between a micro particle A and a particle B of the same kind. When the particle A moves at a velocity 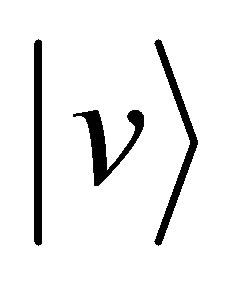and collides at time with the particle B in the standstill state, if we can clarify the distinction between A and B after the collision, the particle A decelerates from the velocity 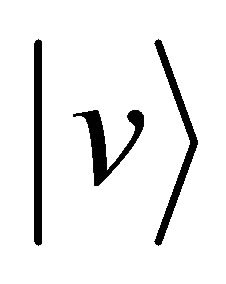to the velocity zero and the particle B accelerates from the velocity zero to the velocity 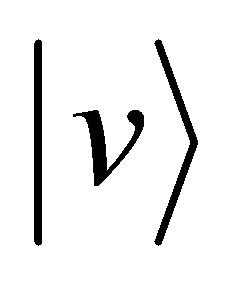between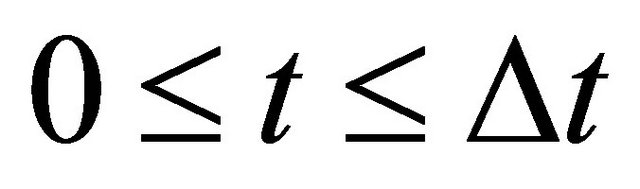. On the other hand, if we cannot clarify the distinction between A and B after the collision, it seems that the particle A decelerates from the velocity to the velocity zero between 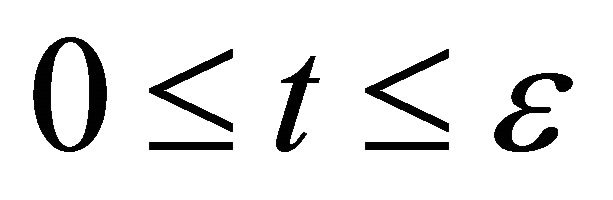and subsequently accelerates again from the velocity zero to the velocity 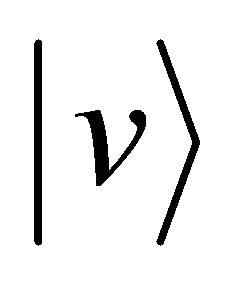between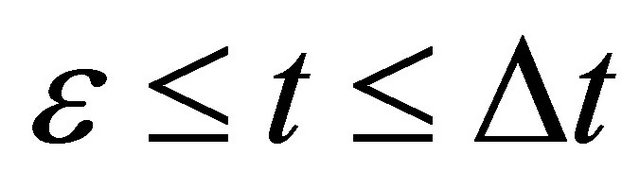. In other words, the particle motion seems as if there is no collision process.

If we notice the acceleration of 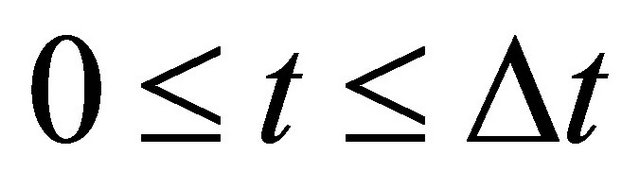in the above latter case, the relation of 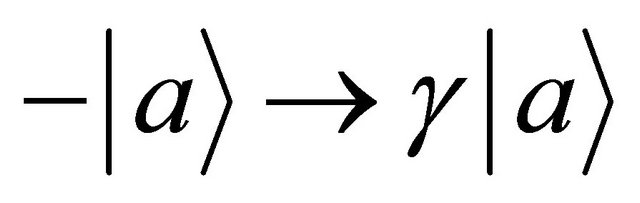between 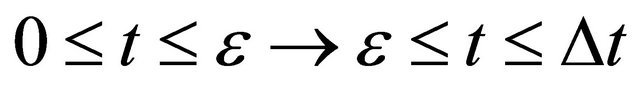is valid in the three dimensional collision process, using a probabilistic parameter 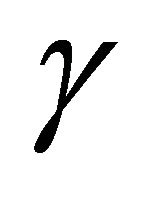of. Therefore, this indicates that the impossibility of discrimination between the particles A and B yields 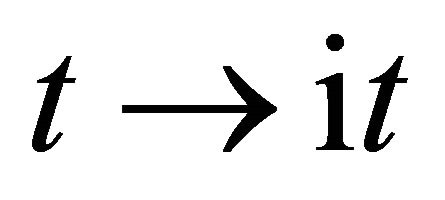or 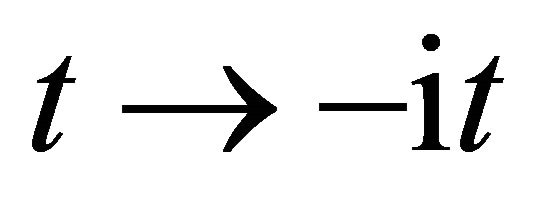between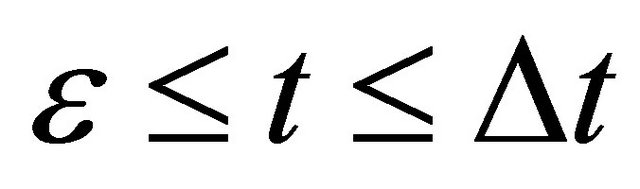, as can be seen from the expression of (5).

In the present study, we thus accept the imaginary time 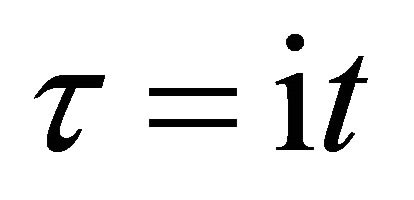as an essential characteristic of a micro particle caused by the impossibility of discrimination between micro particles. In a collision problem, the acceleration is meaningless, although 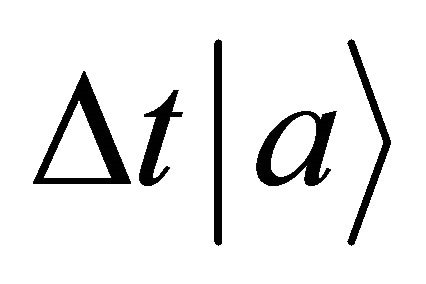is finite at the limit of 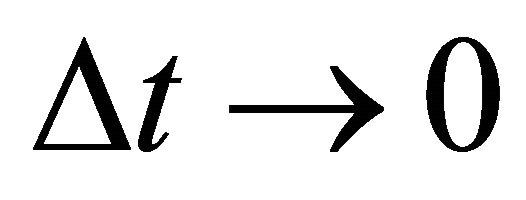and.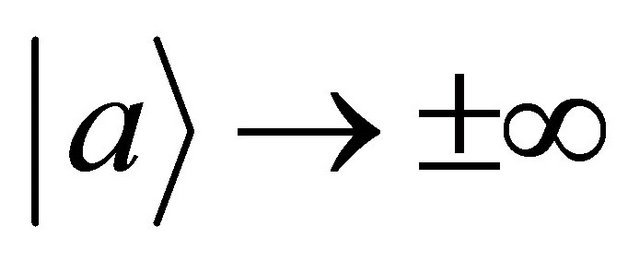

3. Diffusion Equation of Imaginary Time

Rewriting the concentration 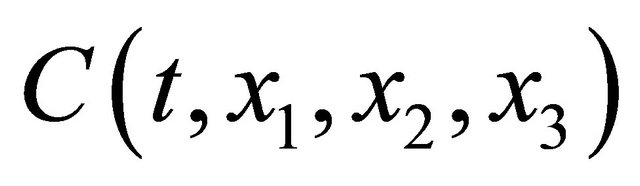of diffusion particles into a quantity of state expressed by a complex function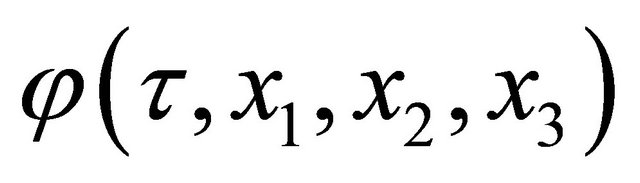, (1) is presented as:

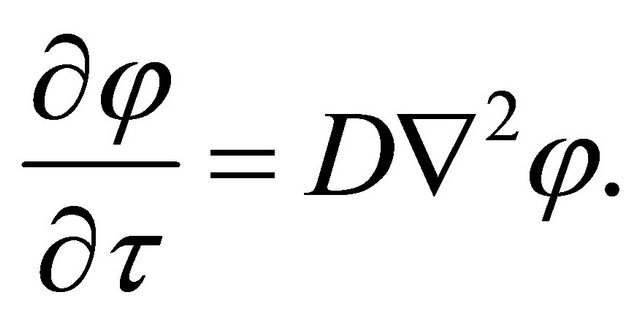(6)

Assuming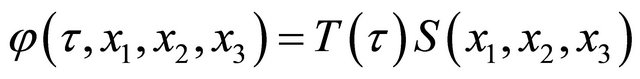, (6) can be solved by the separation method of variables. Using complex numbers 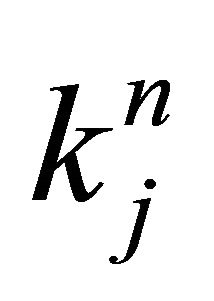and 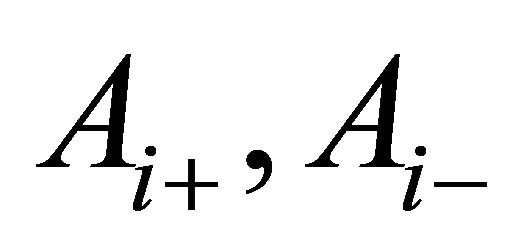determined from the initial and boundary conditions, the general solution of (6) is obtained as;

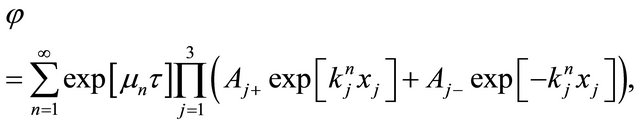(7)

where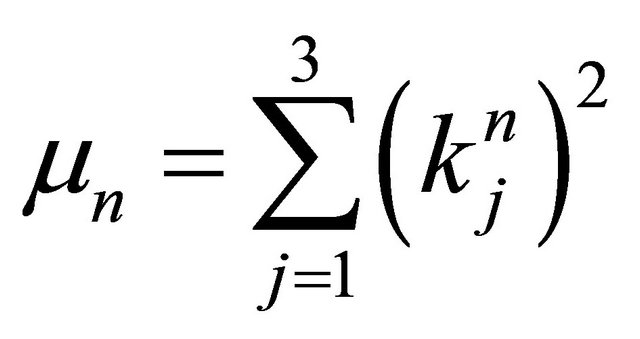. Substituting 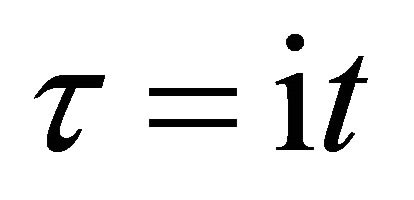into (7), it becomes

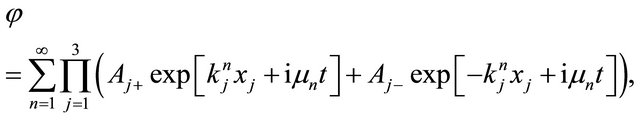
and using the real function 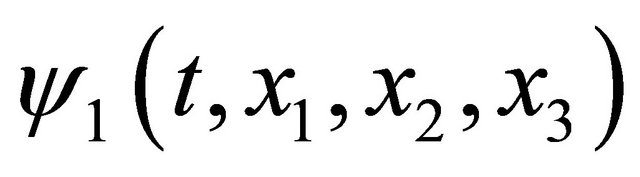and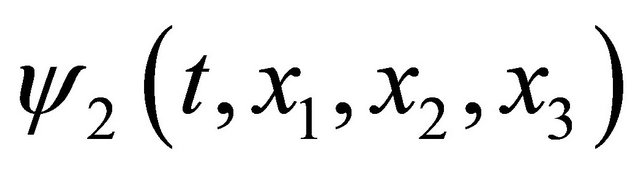, we rewrite the complex function into the complex-value function yielding

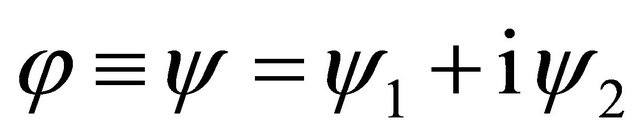. (8)

Further, substituting (8) and into (6) and multiplying the both-side of (6) by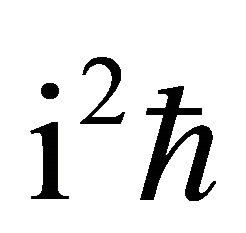, (1) is rewritten as:

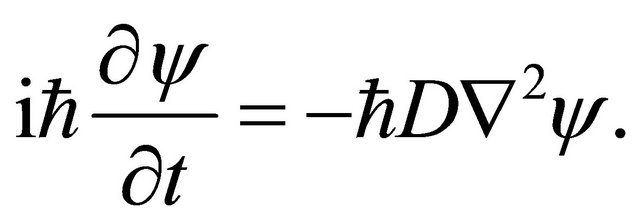(9)

4. Diffusion Coefficient of Micro Particle

The function is defined as a probability density which a diffusion particle in the initial state of 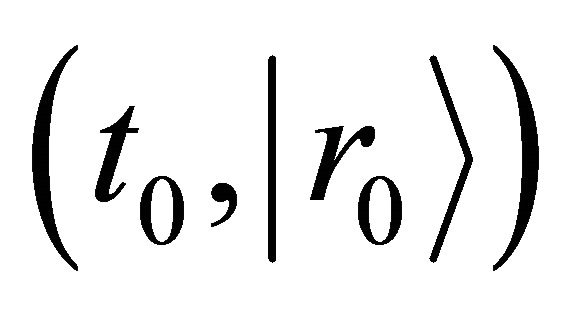exists in the state of 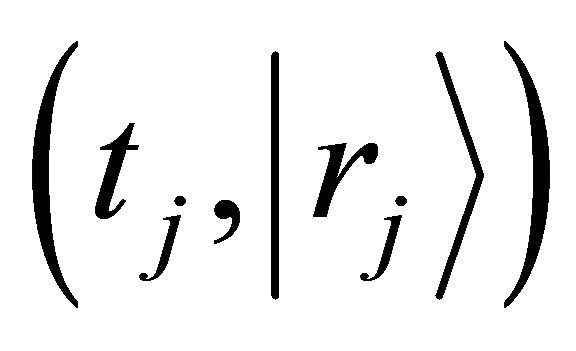after j times jumps. A diffusion particle moves at random and it is, therefore, considered that the jump frequency 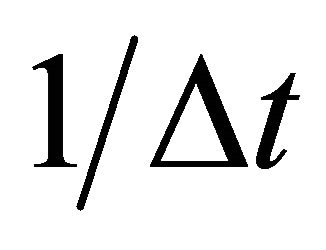and jump displacement 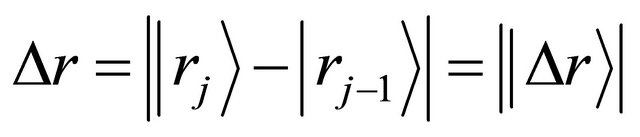are equivalent in probability to their mean values of all diffusion particles in the collective system. Since it is also considered that the probability of diffusion-jump from the state of 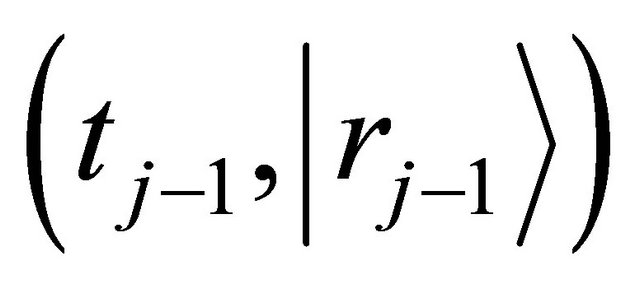to 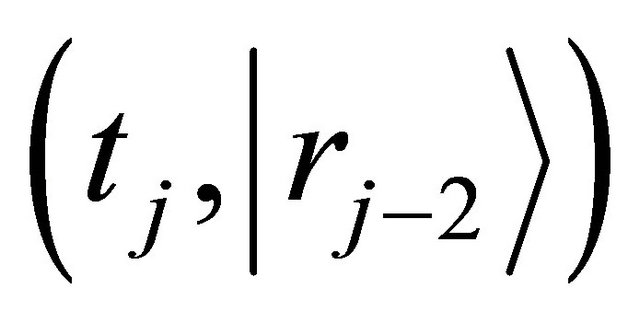is equivalent to one from the same state to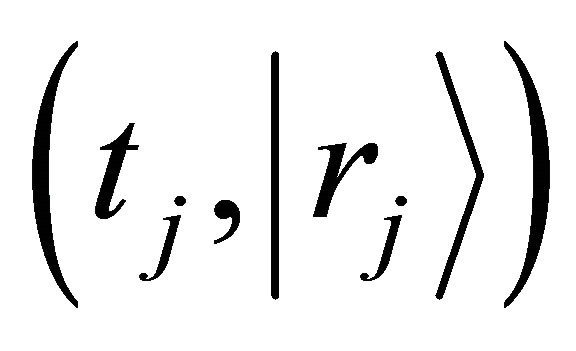, the relation of

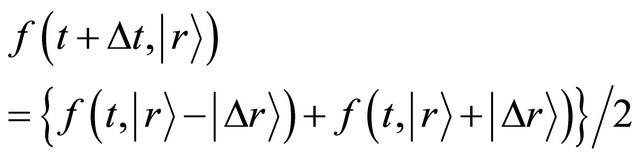(10)

is thus valid.

The Taylor expansion of the left-hand side of (10) yields

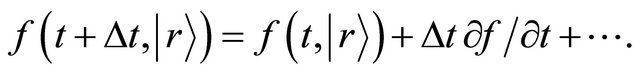(11)

The Taylor expansion of the right-hand side of (10) also yields

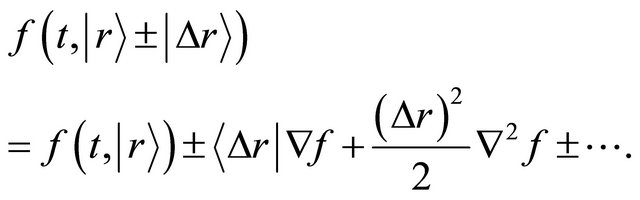(12)

The substitution of (11) and (12) into (10) gives

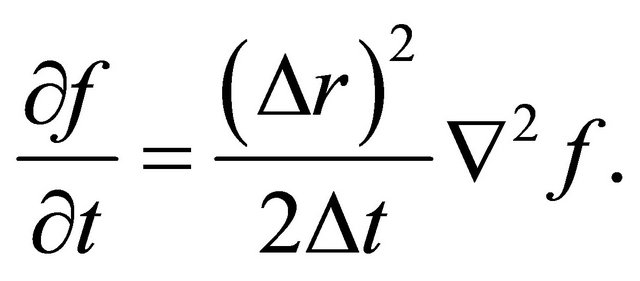(13)

Since the probability density function f of a diffusion particle corresponds to the normalized concentration C, the comparison of (1) with (13) gives the diffusion coefficient yielding

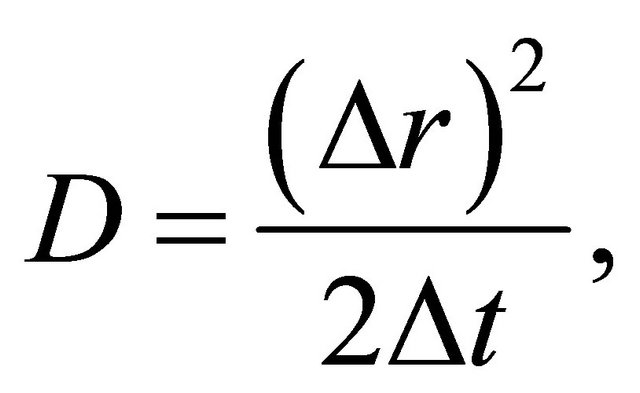(14)

as a relation satisfying the well-known parabolic law [5].

5. Diffusion Coefficient and Angular Momentum

When a micro particle randomly jumps from a position to another one, the jump orientation becomes the spherical symmetry in probability. Using the equation of

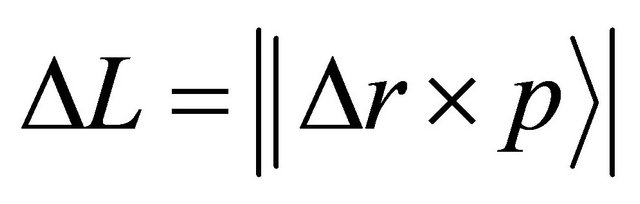
relevant to the angular momentum 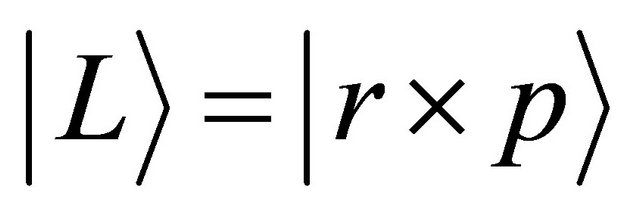defined by a position vector 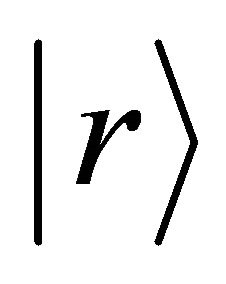and a momentum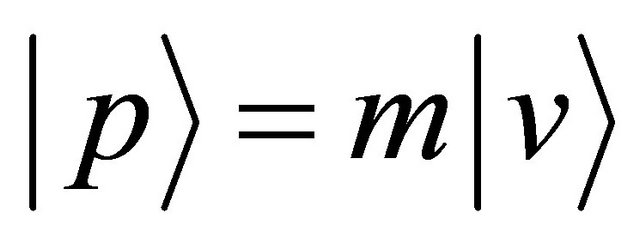, the right-hand side of (14) is rewritten as:

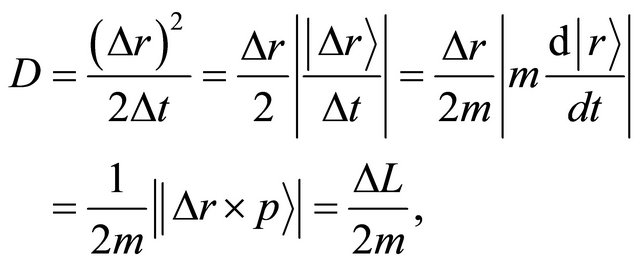
where 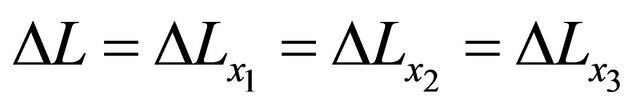is valid in the spherical symmetry space. Considering the eigenvalue, the relation of (14) is thus rewritten as an operator relation of

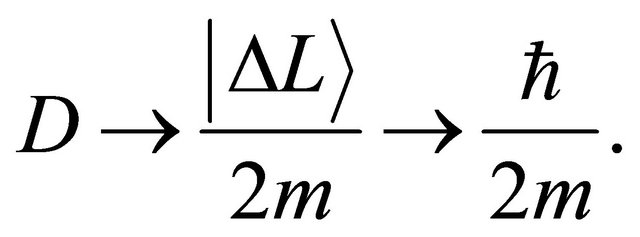(15)

Substituting (15) into (9) gives

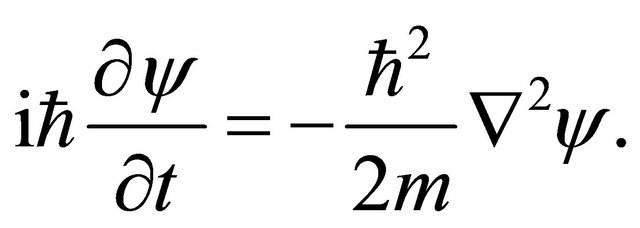(16)

Here, if we define the relation given by

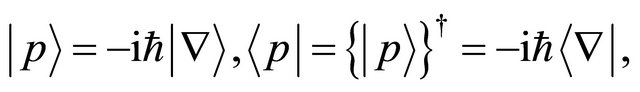(17)

(16) becomes the equation of

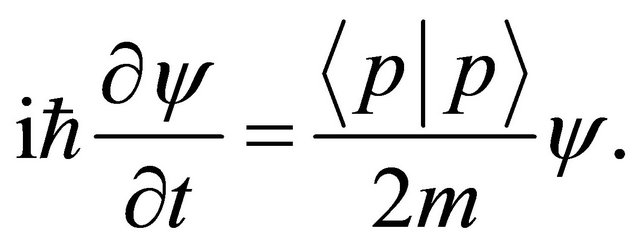(18)

Further, the substitution of (3) into (18) yields the well-known Schrödinger equation (2).The defined equation (17) is one of the basic operators in quantum mechanics.

Hereinbefore, the Schrödinger equation was reasonably derived from the diffusion equation. It was also found that the diffusivity corresponds to the angular momentum operator in quantum mechanics. The relation of (15) is concretely investigated in the following section.

6. Discussion and Conclusion

In mathematics, it was clarified that we can transform the diffusion equation for the collective motion of micro particles into the Schrödinger equation for a micro particle. In physics, energy E, momentum 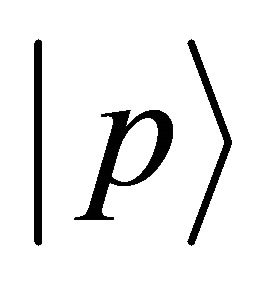and angular momentum 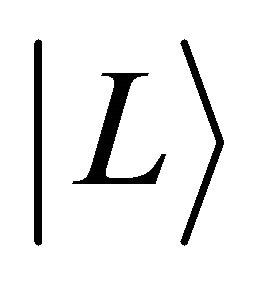are expressed as operators yielding

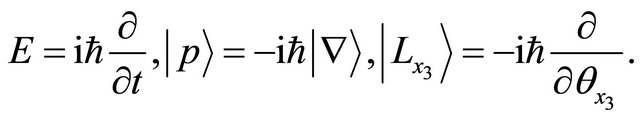
We cannot observe imaginary physical quantities. Therefore, the eigenvalues of their operators are meaningful in quantum mechanics.

As previously mentioned in a collision problem, the impossibility of identification between micro particles corresponds to introducing the imaginary time 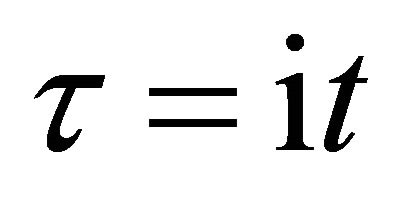into those motions and also it corresponds to yielding the meaningless acceleration. It is considered that the physical concept obtained here is generally valid for the micro particle motions. Thus, the concept of acceleration disappears in quantum mechanics.

Except constant physical quantities, physical variables containing an imaginary number i should be accepted as physical operators in quantum mechanics. Here, note that the kinetic energy 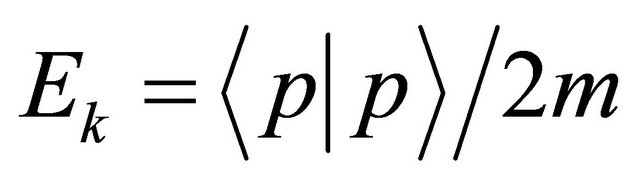in Hamiltonian is acceptable as an operator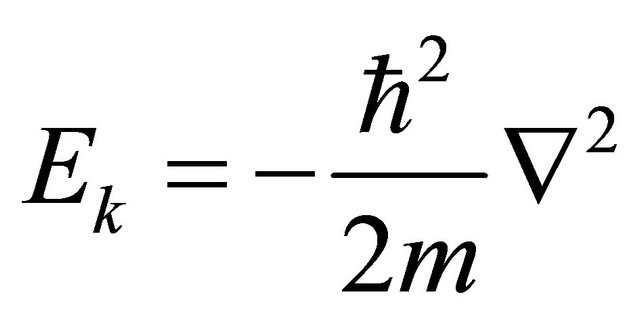. On the other hand, the photon energy 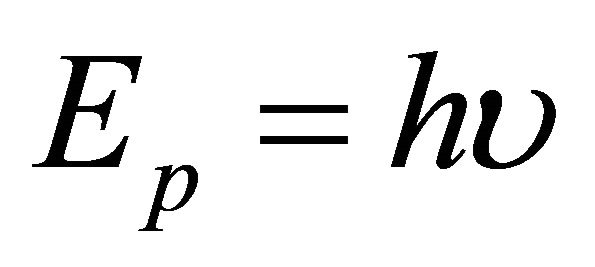expressed by using a frequency is acceptable as an operator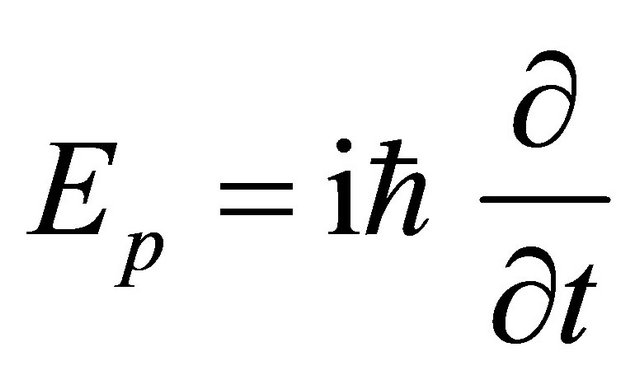although 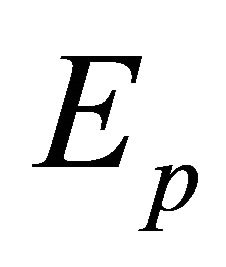as well as 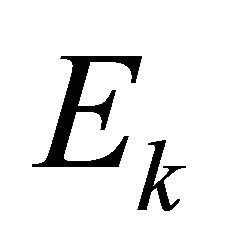is also an energy representation.

The existence probability of a micro particle in a collective system of heat quantity Q and absolute temperature T is given by the well-known Boltzmann factor of

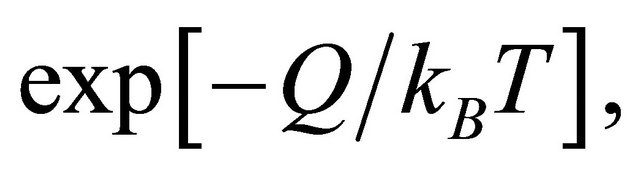(19)

where 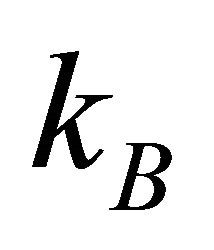is the Boltzmann constant [6]. There is an energy barrier for a diffusion particle in order to jump from a site to another site. Therefore, it is necessary for a diffusion particle to obtain the activation energy Q from the thermal fluctuation. In a collective system composed of micro particles, the diffusion coefficient D is thus directly proportional to the probability factor of (19).

The jump of a diffusion particle in a solid crystal depends on a factor 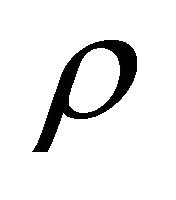derived from the atomic configuration and on the entropy S derived from an elastic strain. In a solid crystal, therefore, (15) is rewritten as

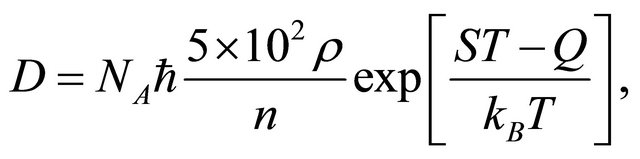(20)

where 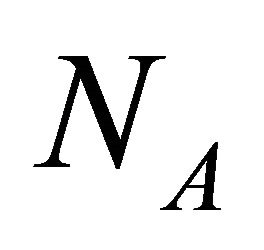and 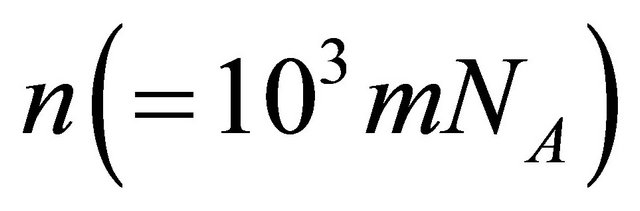are the Avogadro constant and the molecular or the atomic weight. Here, (20) was obtained as a new representation of diffusion coefficient.

If we consider 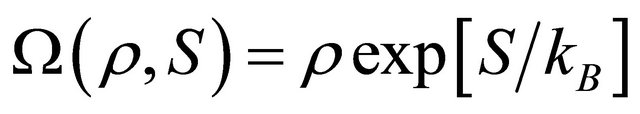in the given diffusion system of an arbitrary material, the universal diffusivity expression of

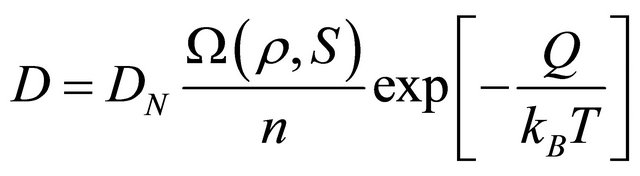(21)

is thus obtained, where.

The correlation between the diffusion equation and Schrödinger equation was clarified. We revealed that the diffusion coefficient D in classical mechanics corresponds to the angular moment in quantum mechanics. The physical constant of

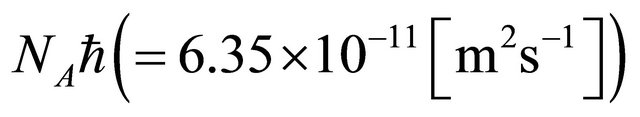in (20) is an essential quantity in the diffusion problems.

REFERENCES