Journal of Modern Physics
Vol. 2 No. 10 (2011) , Article ID: 8055 , 5 pages DOI:10.4236/jmp.2011.210144
Self-Consistent Calculations on the Atomic Electron Affinity and Ionization Energy with Taking Effects of the Nonspherical Distribution of Electrons into Account
1Graduate School of Science and Engineering, Shinshu University, Ueda, Japan
2Graduate School of Advanced Science of Matter, Hiroshima University, Higashi-Hiroshima, Japan
3Department of Physics, Faculty of Science, Shinshu University, Matsumoto, Japan
E-mail: *miyasita.mitiyasu@gmail.com
Received June 3, 2011; revised July 21, 2011; accepted August 8, 2011
Keywords: Nonspherical Distribution of Electrons, Spherical Approximation, Atomic Structure, First-Row Atoms, Electron Affinity, Ionization Energy
ABSTRACT
We perform the self-consistent calculations on the atomic electron affinity and ionization energy for the first-row atoms by means of our scheme. A striking feature of the present work is the variational method with taking into account effects of the nonspherical distribution of electrons explicitly. Comparing the present results with those of the conventional spherical approximation, the systematical improvement can be found. This means that effects of the nonspherical distribution of electrons may play an essential role on the description of the atomic structures.
1. Introduction
The single-particle wave functions and spectra for atomic systems are quite useful for the estimations of the hopping and Coulomb integrals included in the model Hamiltonian [1,2], the LCAO method [3] and the LDA + U method [4,5], etc. In order to obtain these wave functions and spectra, the simplest scheme would be the central field approximation [6], which is sometimes called the spherical approximation. But this approximation obviously has a disadvantage of neglecting effects of the nonspherical distribution of electrons. For the purpose of taking into account such the effects, many kinds of methods have been presented and performed so far [7- 17]. These previous works may be classified into two kinds of approaches. One is the variational method where the single-particle wave function is expanded by using appropriately chosen basis functions [7-9]. Another is the density functional scheme containing the effect of the orbital current density explicitly [10-17].
Recently, we have proposed a sophisticated scheme that is classified into the former approach [18]. The methodological difference from the previous ones [8,9] is the choice of the basis set of the variational method. [18] In this paper, the self-consistent calculations on the atomic electron affinity and ionization energy are performed in order to check the validity of this our scheme, because the electron affinity and ionization energy are key quantities that can be directly compared with experiments in atomic physics. Here, it should be noted that the validity of the Hartree-Fock-Slater (HFS) approximation, which is adopted also in this work, can be identified from previous our work [18] and the Narita’s work [19]. Actual calculations are done for the first-row atoms, i.e., boron, carbon, nitrogen, oxygen and fluorine atoms.
Comparing the present results with those of the conventional spherical approximation, the systematical improvement can be found due to the consideration of effects of the nonspherical distribution of electrons. Hereafter, we shall explain the outline of our scheme and show the details of the calculation results.
2. Method
In our recent work [18], we have proposed a scheme for calculating atomic single-particle wave functions and spectra with taking into account effects of the nonspherical distribution of electrons explicitly. We shall sketch out this scheme. Neglecting relativistic effects, we start from the HFS Equation [20-22] as an effective single-particle equation,
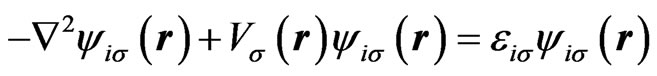 (1)
(1)
where,
 (2)
(2)
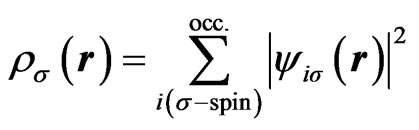 (3)
(3)
where  and
and 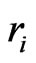 stand for the position of the ith electron and its magnitude, respectively, and where
stand for the position of the ith electron and its magnitude, respectively, and where 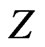 is the atomic number. Here, the atomic unit is used.
is the atomic number. Here, the atomic unit is used.
First, we expand the effective potential with the spherical harmonics,
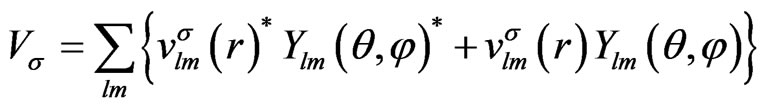 (4)
(4)
where 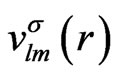 are the radial components and their explicit forms are given in Appendix. In a similar way, we shall expand the solution of the HFS equation with the set of known basis functions,
are the radial components and their explicit forms are given in Appendix. In a similar way, we shall expand the solution of the HFS equation with the set of known basis functions,
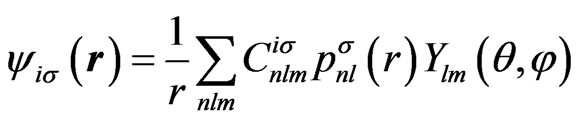 (5)
(5)
As the known functions, the eigenfunctions for the spherically-averaged potential,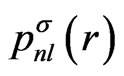 , are adopted. These radial wave functions are calculated easily by means of the numerical methods such as the HermanSkillman method [23]. In this expansion, we use five functions having the following quantum numbers:
, are adopted. These radial wave functions are calculated easily by means of the numerical methods such as the HermanSkillman method [23]. In this expansion, we use five functions having the following quantum numbers: 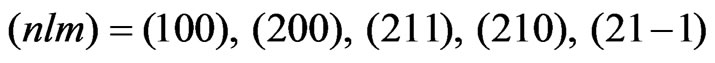 .Correspondingly, the upper limit of the potential given by Equation (4) is determined from the properties of the Wigner 3j symbols [6]. The expansion of the potential consists of the following terms:
.Correspondingly, the upper limit of the potential given by Equation (4) is determined from the properties of the Wigner 3j symbols [6]. The expansion of the potential consists of the following terms:
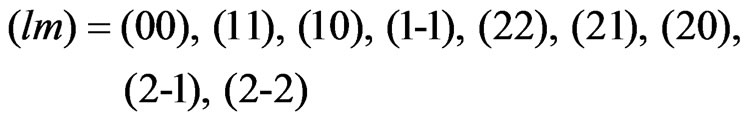 .
.
Substituting Equations (4) and (5) into Equation (1), and multiplying ![]() on both sides and integrating over the whole space, we finally arrive at the generalized eigenvalue problem.
on both sides and integrating over the whole space, we finally arrive at the generalized eigenvalue problem.
Calculation procedure is as follows. We first give a starting potential in some usual way, for example via the LDA calculation within the spherical approximation. Using these solutions as the basis functions of Equation (5), the generalized eigenvalue problem is solved. The resultant new solutions yield the potentials of the next step. The calculations are repeated until the potentials are converged within some accuracy. These calculations are performed by means of the standard self-consistent-field (SCF) procedures [20].
3. Calculation Results
Using our scheme [18], self-consistent calculations are performed for the first-row neutral atoms and their negative/positive ions. Of course, effects of the nonspherical distribution of electrons are considered explicitly. The self-consistent solutions (SCSs) can be obtained for each case of neutral and ionized atoms. The total energies are calculated by taking the expectation values of the manyelectron Hamiltonian with respect to the single Slater determinant which are constructed from the SCSs. The electron affinities and ionization energies for these atoms are estimated by taking the difference of the total energy between the neutral atom and negative/positive ion. The calculation results are given in Tables 1 and 2, together with those of the conventional spherical approximation.
From Tables 1 and 2, it can be seen that the results of the spherical approximation are quite far from experiments [24,25]. To put it another way, the conventional spherical approximation is too rough to evaluate the electron affinity and ionization energy. For example, experiments of the electron affinities show the minimum value at nitrogen atom, while the spherical approximation takes the maximum value. Also experiments of the ionization energies show the monotony decrease, while the spherical approximation shows a complicated behavior. This may be due to the lack of effects of the non-spherical distribution of electrons, because the experi-

Table 1. Electron affinities for the first-row atoms. All values are given in eV. The first and second columns show the results for the usual spherical approximation and the present scheme, respectively. The third column gives the experimental results [24].

Table 2. Ionization energies for the first-row atoms. All values are given in eV. The first and second columns show the results for the usual spherical approximation and the present scheme, respectively. The third column gives the experimental results [25].
mental trends are well reproduced by the present scheme (see Figures 1 and 2). The present scheme can explain the electron affinities and ionization energies for all of the first-row atoms better than the conventional spherical approximation. Here, it should be noted that these comparisons are done within the same approximation for the exchange potential, i.e., HFS approximation.
Thus, these better agreements shown in Tables 1, 2 and Figures 1, 2 suggest that effects of the nonspherical distribution of electrons is indispensable for describing the atomic structures.
4. Concluding Remarks
In this paper, we perform the self-consistent calculations on the atomic electron affinity and ionization energy with taking into account effects of the nonspherical distribution of electrons explicitly. Comparing the present results with those of the conventional spherical approximation, the improvements can be found in a series of the first-row atoms systematically.
Of course, the present work is not a goal, and there is a room for improvement in our scheme. To obtain a better
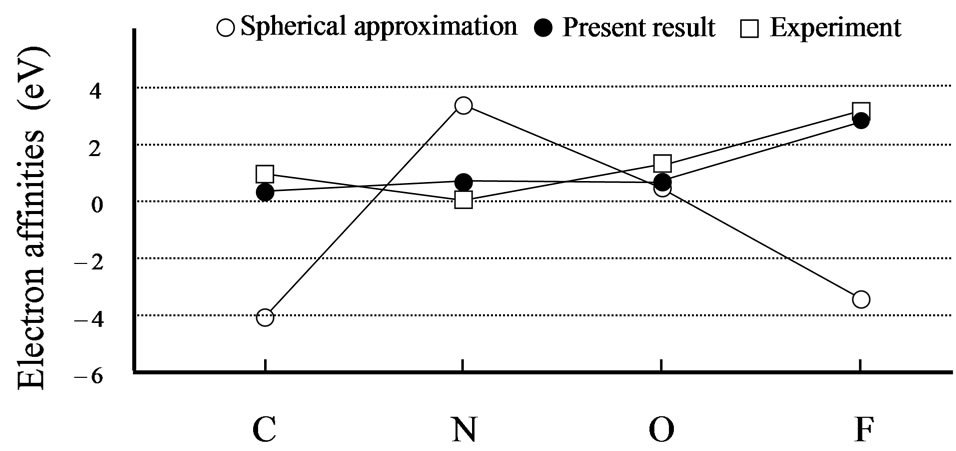
Figure 1. Experimental [24] and calculated electron affinities in eV. The open and close circles denote the calculation results for the spherical approximation and the present scheme, respectively. The open squares are the experimental results. Lines are just guides for eyes.

Figure 2. Experimental [25] and calculated ionization energy in eV. The open and close circles denote the calculation results for the spherical approximation and the present scheme, respectively. The open squares are the experimental results. Lines are just guides for eyes.
accuracy of the electron affinity and ionization energy, we have to consider the following effects that are neglected in the present calculations:
1) truncation errors of the expansion in Equation (5)2) treatment of the exchange energy beyond the Hartree-Fock-Slater approximation3) electron correlation effects.
Concerning the first effect, we here adopt only 1 s, 2 s and 2 p orbitals in the expansion of the eigenfunctions. However, in order to reduce the truncation errors, we had better take more functions as the basis functions. Similarly, the second and third effects seem to be indispensable for describing effects of the nonspherical distribution of electrons in more detail.
But anyway, we can say within the knowledge obtained in this paper that effects of the nonspherical distribution of electrons may play an essential role on the description of the atomic properties such as electron affinity and ionization energy.
5. Acknowledgements
This work was partially supported by Grant-in-Aid for Scientific Research (No. 19540399) and for Scientific Research in Priority Areas (No. 17064006) of The Ministry of Education, Culture, Sports, Science, and Technology, Japan.
REFERENCES
- N. F. Mott, “The Basis of the Electron Theory of Metals, with Special Reference to the Transition Metals,” Proceedings of the Physical Society, London, Section A, Vol. 62, No. 7, 1949, p. 416.
- P. W. Anderson, “New Approach to the Theory of SuperExchange Interactions,” Physical Review, Vol. 115, No. 1, 1959, pp. 2-13. doi:10.1103/PhysRev.115.2
- W. A. Harrison, “Electronic Structure and the Properties of Solids—The Physics of the Chemical Bonds,” W. H. Freeman and Co., San Francisco, 1980.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, “Band Theory and Mott Insulators: Hubbard U instead of Stoner,” Physical Review B, Vol. 44, No. 3, 1991, pp. 943-954. doi:10.1103/PhysRevB.44.943
- A. I. Liechtenstein, V. I. Anisimov and J. Zaanen, “Density-Functional Theory and Strong Interations: Orbital Ordering in Mott-Hubbard Insulators,” Physical Review B, Vol. 52, No. 8, 1995, pp. R5468-R5470. doi:10.1103/PhysRevB.52.R5467
- A. Messiah, “Quantum Mechanics,” Dover Publications, New York, 1999.
- J. C. Slater, “The Calculation of Molecular Orbitals,” John Wiley & Sons, New York, 1979.
- J. F. Janak and A. R. Williams, “Method for Calculating Wave Functions in a Nonspherical Potential,” Physical Review B, Vol. 23, No. 12, 1981, pp. 6301-6306. doi:10.1103/PhysRevB.23.6301
- F. W. Kutzler and G. S. Painter, “Energies of Atoms with Nonspherical Charge Densities Calculated with Nonlocal Density-Functional Theory,” Physical Review Letters, Vol. 59, No. 12, 1987, pp. 1285-1288. doi:10.1103/PhysRevLett.59.1285
- A. D. Becke, “Local Exchange-Correlation Approximations and First-Row Molecular Dissociation Energies,” International Journal of Quantum Chemistry, Vol. 27, No. 5, 1985, pp. 585-594. doi:10.1002/qua.560270507
- A. D. Becke, “Current Density in Exchange-Correlation Functionals: Application to Atomic States,” Journal of Chemical Physics, Vol. 117, No. 15, 2002, pp. 6935- 6938. doi:10.1063/1.1503772
- E. Orestes, T. Marcasso and K. Capelle, “Density-Functional Calculation of Ionization Energies of CurrentCarrying Atomic States,” Physical Review A, Vol. 68, No. 2, 2003, p. 022105. doi:10.1103/PhysRevA.68.022105
- E. Orestes, A. B. F. da Silva and K. Capelle, “Energy Lowering of Current-Carrying Single-Particle States in Open-Shell Atoms Due to an Exchange-Correlation Vector Potential,” International Journal of Quantum Chemistry, Vol. 103, No. 5, 2005, pp. 516-522. doi:10.1002/qua.20575
- G. Vignale and M. Rasolt, “Density-Functional Theory in Strong Magnetic Fields,” Physical Review Letters, Vol. 59, No. 20, 1987, pp. 2360-2363. doi:10.1103/PhysRevLett.59.2360
- G. Vignale and M. Rasolt, “Currentand Spin-DensityFunctional Theory for Inhomogeneous Electronic Systems in Strong Magnetic Fields,” Physical Review B, Vol. 37, No. 18, 1988, pp. 10685-10696. doi:10.1103/PhysRevB.37.10685
- M. Higuchi and A. Hasegawa, “A Relativistic Current and Spin-Density Functional Theory and a Single-Particle Equation,” Journal of the Physical Society of Japan, Vol. 66, No. 1, 1997, p. 149. doi:10.1143/JPSJ.66.149
- M. Higuchi and A. Hasegawa, “Single-Particle Equation of Relativistic Currentand Spin-Density Functional Theory and Its Application to the Atomic Structure of the Lanthanide Series,” Journal of the Physical Society of Japan, Vol. 67, No. 6, 1998, pp. 2037-2047. doi:10.1143/JPSJ.67.2037
- M. Miyasita, K. Higuchi and M. Higuchi, “A Scheme for Calculating Atomic Structures beyond the Spherical Approximation,” Journal of Modern Physics, Vol. 2 No. 5, 2011, pp. 421-430. doi:10.4236/jmp.2011.25052
- A. Narita, “Nonspherical Potential due to Orbital Polarization and Its Effect in Atoms—Approach to Hund’s Second Rule in Terms of One-Electron Picture,” Journal of the Physical Society of Japan, Vol. 77, 2008, p. 124303. doi:10.1143/JPSJ.77.124303
- D. R. Hartree, “The Wave Mechanics of an Atom with a Noncoulomb Central Field. Part I: Theory and Method. Part II: Some Results and Discussions,” Proceedings of Cambridge Philosophical Society, Vol. 24, No. 1, 1928, pp. 111-132. doi:10.1017/S0305004100011920
- V. Fock and Z. Physik, “Näherungsmethode zur Lösung des Quantenmechanischen Mehrkörperproblems,” Zeitschrift Für Physik, Vol. 61, No. 1-2, 1930, pp. 126-148.
- J. C. Slater, “A Simplification of the Hartree-Fock Method,” Physical Review, Vol. 81, No. 3, 1951, pp. 385- 390. doi:10.1103/PhysRev.81.385
- F. Herman and S. Skillman, “Atomic Structure Calculations,” Prentice-Hall Inc., New Jersey, 1963.
- T. Andersen, H. K. Haugen and H. Hotop, “Binding Energies in Atomic Negative Ions: III,” Journal of Physical and Chemical Reference Data, Vol. 28, 1999, p. 1511. doi:10.1063/1.556047
- See Instance. http://physics.nist.gov/PhysRefData/IonEnergy/tblNew.html.
Appendix
Expressions for the Potentials
In this appendix, we give the expressions for the spherical part of the effective potential,  , and the expansion coefficients of the effective potential,
, and the expansion coefficients of the effective potential,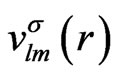 .
.
Using the present expression for the wave functions (5), above-mentioned potentials are, respectively, calculated as
 (A1)
(A1)
 (A2)
(A2)
with
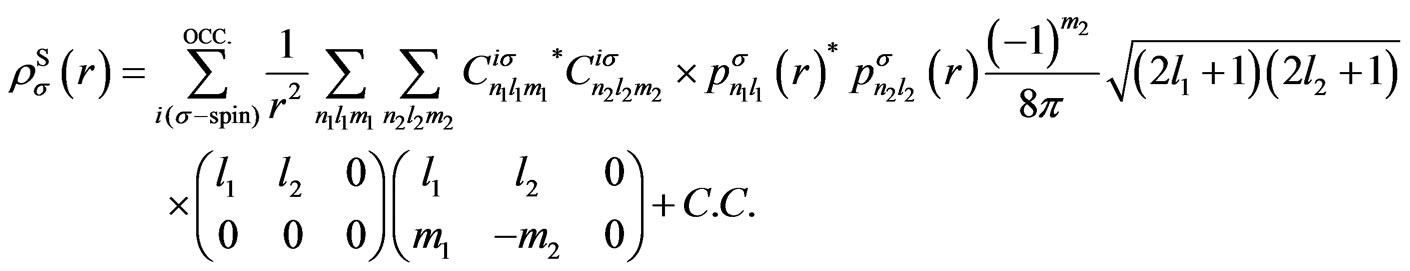 (A3)
(A3)
Here 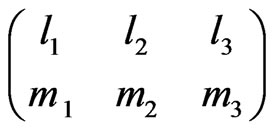 is the Wigner 3j symbol [6].
is the Wigner 3j symbol [6].

