Received 23 December 2015; accepted 25 January 2016; published 28 January 2016

ABSTRACT

In this paper, a discretized SIR model with pulse vaccination and time delay is proposed. We introduce two thresholds R^* and R_*, and further prove that the disease-free periodic solution is globally attractive if R^* is less than unit and the disease can invade if R_* is larger than unit. The numerical simulations not only illustrate the validity of our main results, but also exhibit bifurcation phenomenon. Our result shows that decreasing infection rate can put off the disease outbreak and reduce the number of infected individuals.

Keywords:

Discrete Epidemic Model, Time Delay, Pulse Vaccination, Extinction

1. Introduction

Infectious diseases have a great influence on the human life and socio-economy, which lead many scientists to implement more effective measures and preparedness programs. Pulse vaccination strategy (PVS) is the one of important methods to control disease, such as hepatitis B, parotitis and encephalitis B. From the theoretical results we can know that the PVS can be distinguished from the conventional strategies in leading to disease eradication at relatively low values of vaccination [1] . And one investigates under what conditions given agent can invade partially vaccinated population, i.e., how large a fraction of the population do we have to keep vaccinated in order to prevent the agent from establishing. Then a number of epidemic models in ecology can be formulated as dynamical systems of differential equation with pulse vaccination [2] -[6] , of which the SIR infectious disease model is an important biologic model.

A model for the spread of an infectious disease (involving only susceptible and infective individuals) trans- mitted by a vector after an incubation time was proposed by Cook [7] . This is called the phenomena of time delay which has very important biologic meaning in epidemic models. But for the system, many authors don’t put to use the distributed delay. Because the distributed delay allows infectivity to be a function of the duration since infection up to some maximum duration. Comparing with the time be a fixed time, the distributed delay is more appropriate form and more realistic. Beretta and Takeuchi [3] did study the following continuous SIR model with distributed delay, without considering the pulse vaccination strategy:

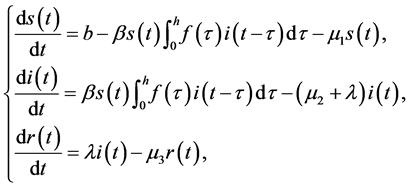(1)

where the infectiousness is assumed to vary over time from the initial time of infection until a duration h has passed and the function means the fraction of vector population in which the time taken to become infectious is t.

For simplicity, they let 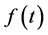be nonnegative and continuous on 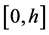and assume that.

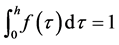In the decade years, many authors have directly studied the delay SIR epidemic models with time delays and pulse vaccination [8] -[11] . In 2010, Yanke Du and his co-workers [9] have studied an SIR epidemic model with nonlinear incidence rate and pulse vaccination:

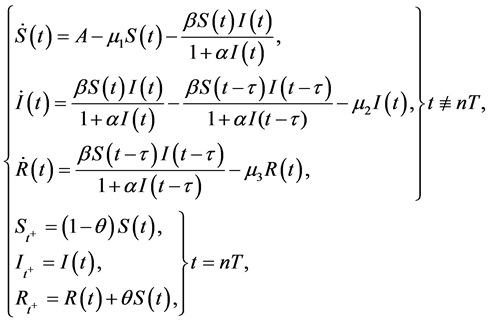(2)

where all coefficients are positive constants. A represents the recruitment rate assuming all newborns to be susceptible. 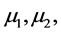and represent the death rates of susceptible, infectious, and recovered, respectively. 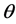(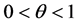) is the proportion of those vaccinated successfully, which is called impulsive vaccination rate. 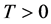is the period of pulsing. Considering the nonlinear incidence rate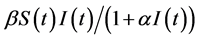, they have found the basic reproduction 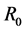and obtain an infection-free periodic solution for the system. More importantly, they certified that if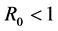, it is globally attractive, and if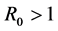, the system is permanent. But they did not study the the distributed delay. This is partly because the system is with nonlinear incidence rate and pulse vaccination, then investigation of global behavior for with the effect of saturation incidence and distributed time delay on the SIR epidemic model with a pulse vaccination is challenging.

The incidence rate plays an important role in the epidemic models. In many epidemic models, the Bilinear incidence is based on the law of mass action. This contact law is more appropriate for communicable diseases such as influenza, but not for sexually transmitted diseases. For standard incidence, it may be a good approximation if the number of available partners is large enough and everybody could not make more contacts than practically feasible. In [12] , Capasso and Serio introduced a saturated incidence rate into epidemic models after studying the cholera epidemic spread in Bari in 1973, where measures the infection force of the disease and measures the inhibition effect from the behavioral change of the susceptible individuals when their number increases. That is to say,the saturated incidence rate tends to a saturation level when I gets large. Comparing with bilinear and standard incidence, saturation in- cidence may be more suitable for our real world.

On the other hand, numerical simulation is usually used to assess all kinds of continuous models and check our theoretical results. But, the statistical data of epidemic is collected and reported in discrete time, such as daily, weekly, monthly or yearly. Sometimes, they may fail generating oscillations, bifurcations, chaos and false steady states [13] . In order to be more in line with the actual, many authors are hoping to discuss discretized models, which always exhibit richer and more complicated dynamical behaviors than continuous models. For example, Masaki and Emiko [14] have used the nonstandard finite difference scheme to study the dynamics of a discretized SIR epidemic model with pulse vaccination and time delay:

(3)

where and () are susceptible, infective and recovered with permanent immunity classes at nth step individually. is a positive step size. The constant represents the immigration rate, assuming all newborns to be susceptible. r is the recovery rate. Note that the delay and the period of pulsing are positive integers, and the parameter is the proportion of those vaccinated successfully.

To prevent these classes of numerical instabilities, as one of numerical schemes, the nonstandard finite- difference scheme, developed by Mickens [15] - [17] , has been applied to various problems in science [18] - [21] . By using this kind of scheme [16] , it leads to asymptotic dynamics and numerical results are always qualita- tively the same as the corresponding solutions of several ordinary differential equations for any positive step size. More importantly, This scheme has brought the creation of new numerical schemes that preserve the pro- perties of the continuous model [2] [3] [6] [8] [10] [13] [22] .

Motivated by the work of [3] [9] [14] , in this paper, we are considered with the effect of saturation incidence and distributed time delay on the dynamics of a discrete SIR epidemic model with pulse vaccination:

(4)

where all coefficients are positive constants. and () are also susceptible, infective and recovered with permanent immunity classes at nth step individually. is a constant integer, and is

the infected period, are weighting coefficients and. The notations of other para- meters are the same as system (3).

In this paper, the structure of the layout is as follows. In the next section, we mainly obtain the positivity and boundedness of the solution of the system. Furthermore, we give some important conclusions so as to make matting for the Section 3. In Section 3, we analyzed the existence and global behavior of the infection-free periodic solution of the system. The permanence of our model is discussed in Section 4. Our results are the same to Theorems 1 and 2 in system (2). In Section 5, we show some numerical experiments which have verified our theoretical results.

2. Basic Properties and Preliminaries

Noting that the variable R does not appear in the first two equations of system (4), it is sufficient to consider the following 2-dimensional system.

(5)

Let The initial conditions of the system (5) are given by

(6)

For the reduced system (5), at first, we show that the solution has positivity for, and bounded above for sufficiently large n.

Lemma 1. Let be a solution of system (5), with the initial conditions (6), then and for all. And any solution of system (5) satisfies, where.

Proof. From the initial condition (6) and the first and second equations of system (5), we have

(7)

and

(8)

Let. It follows from (7) that x satisfies the following equation

Since is monotonically increasing with respect to x, and,. Therefore, there exists a unique such that. This shows that.

From (8), we can directly obtain.

From the above discussions, we finally have and.

When, from model (5) we have

and

A similar argument as in the above proof for and, we also can obtain that and. By using the induction, we can finally obtain that and for. Moreover, for. Therefore we can easily obtain that and for all.

From the system (5), we have

Thus

where. Consider the following comparison system

(9)

Obviously, system (9) has a globally asymptotically stable equilibrium. Hence, according to the comparison principle of the difference equations, we have that

(10)

This shows that is also ultimately bounded. This completes the proof. □

Lemma 2 [14] . Let us consider the following impulsive difference equations:

(11)

where. Then system (11) has a unique positive periodic solution

which is globally asymptotically stable.

Lemma 3. Consider the following equation

(12)

where. We have

(i) if, then;

(ii) if, then.

Proof. From (12), we have

It is obvious that for all.

Denote. From (12), we can also obtain

Suppose that

Then we further have

By Mathematical induction, we can get for any, there exist, and such that

So, if.

By the similar arguments to above steps, we can obtain that for any, there exist, and such that and if. The Lemma 3 is com- pleted. □

3. Global Attractivity of Infection-Free Periodic Solution

In this section, we begin to analyze system (5) by first demonstrating the existence of an infection-free periodic solution, in which infectious individuals are entirely absent from the population permanently.

(13)

By Lemma 2, we know that periodic solution of system (13)

(14)

which is globally asymptotically stable.

Theorem 4. If, then the infection-free periodic solution of system (5) is globally attractive, where

Proof. Since, we can choose sufficiently small such that

(15)

From the first equation of system (5), we have

Then we consider the following comparison system with pulses:

(16)

From Lemma 2, we have that the periodic solution of (16)

is globally asymptotically stable. Let be the solution of system (5) with initial value (6) and, and be the solution of system (16) with initial value. According to the non-negativity of and, there exists an integer such that

(17)

that is for all,

(18)

Further, from the second equation of system (5), we have

(19)

for. Then we consider the following comparison equation:

(20)

From (15) and Lemma 3, we have.

Let be the solution of (20). We choose a constant value as the initial conditions and . By the non-negativity of and. Therefore, for any sufficiently small, there exists an integer, such that for all. From the first equation of system (5), we have

Consider the following comparison system with pulse:

(21)

From Lemma 2, we obtain the globally asymptotically stable periodic solution of (21), i.e.

Let be the solution of (21) with initial value (6) and, and be the solution of system (16) with initial value. By the non-negativity of and, there exists an integer such that

(22)

Since and are sufficiently small. From (17) and (22), we know that

is globally attractive.

Hence, the infection-free periodic solution of system (5) is globally attractive. The proof is com- pleted. □

4. Permanence

In this section, we obtain sufficient condition for permanence of system (5). Denote two quantities

and

(23)

where, and is defined in Theorem 4. Obviously, if.

Theorem 5. Suppose. Then there is a positive constant q such that each solution of system (5) satisfies

Proof. Let be any solution of system (5) with initial condition (6). We claim that for any, it is impossible that for all. Suppose that the claim is not valid. Then there is a such that for all.

It follows from the first equation of (5), that for,

(24)

Consider the following comparison impulsive system for,

(25)

By Lemma 2, we know that the periodic solution of system (25)

(26)

which is globally asymptotically stable.

From (26), we can get

(27)

Let be the solution of system (5) with initial values (6), be the solution of system (25) with ini-

tial value. By comparison theorem, we know that, for, there exists such

that the following inequality holds for

It follows from (27) that

(28)

for. It follows from (23) and (28) that for,

(29)

Set

We will show that for all. Suppose the contrary. Then there is a such that for and.

(30)

This is a contradiction. Thus, for all.

Let us consider any positive solution of system (5). According to this solution, we define

(31)

and

(32)

Since

(33)

It follows from (29), we have that for,

(34)

which implies that as. This contradicts. Hence, the claim is proved.

By the claim, we are left to consider two cases.

Case 1. for all large n. The conclusion is evident in this case.

Case 2. oscillates about for all large n. Set and satisfy

Let be the smallest integer such that is strictly exceeding.

Denote

Subcase 2.1. If, then from the second equation of the system (5), for, we have

(35)

Subcase 2.2. If, we shall consider the following two subcases, respectively.

(a) If, it follows from (35) that;

(b) If, we firstly claim that for.

From the first equation of comparison system (25) for, we obtain

(36)

where is the number of immediately after the kth pulse vaccination at time. Using the second equation of (25), we reduce the stroboscopic map such that

Therefore, by using the stroboscopic map and (27) we can derive for,

(37)

and from (36), we also obtain that

(38)

It follows from (37)and (38) that for,

(39)

where is the solution of system (5) with, and is the solution of comparison system (25) with. Obviously, (39) implies that (28) holds when. Then, proceeding exactly as the proof for the above claim, we see that for. Since these positive integer and are chosen in arbitrary way, we conclude that for all large n. This proof is com- pleted. □

Theorem 6. System (5) is permanent provided that.

Proof. Denote be any solution of system (5) with initial condition (refc1:cond). From the first equ- ation of system (5), we have

for sufficiently large n. Consider the following comparison system:

(40)

According to Lemma 2, we know that for any sufficiently small, there exists a sufficiently large such that

for all. By Lemma 1 and Theorem 5, we can obtain system (5) is permanent. The proof of Theorem 6 is complete. □

5. Numerical Simulation and Discussion

We have formulated a discretized SIR epidemic model with pulse vaccination and time delay. We establish some threshold conditions for permanence and extinction of the disease. To illustrate the analytical results, we do some numerical simulations.

Set, , , , , , , , , then system (5) becomes

Let, then. According to Theorem 4, we know that the disease will die out (see Figure 1). Let, then. According to Theorem 5, we know that the disease will be permanent (see Figure 2).

Figure 3 shows a bifurcation diagram for stroboscopic map of system (2.1) with the infection rate as the bifurcation parameter. This is illustrated in Figure 4 by the curve (the number of infection individuals at the equilibrium) that varies with. We can observe that the value of increases as increases, and is hypersensitive when, or else it is insensitive.

Figure 4 shows a bifurcation diagram for stroboscopic map system (2.1) with pulse vaccination rate as the bifurcation parameter (for which). In this case, numerical result implies that there is unique positive equilibrium of stroboscopic map for all, that is, there is a positive periodic solution of system (2.1) for all. As Figure 5 and Figure 6 shown, it can be seen that the positive equilibrium is globally attractive.

Therefore, an interesting open problem is proposed whether we can prove that the positive periodic solution of model (2.1) is globally attractive as.

Finally, the numerical simulations of the stroboscopic map of model on the number of infected individuals with different values of are shown in Figure 7. It shows that the number of infected individuals will in- crease steadily in next few days, then reach the peak and begin a slow decline, and finally become stable. The greater the value, the bigger the peak value and the earlier the peak appears. Our result implies that decreas- ing infection rate can put off the disease outbreak and reduce the number of infected individuals.

Acknowledgements

The research has been supported by the Natural Science Foundation of China (11261004, 11561004), the Sci- ence and Technology Plan Projects of Jiangxi Provincial Education Department (GJJ14673) and the Social Sci- ence Planning Projects of Jiangxi Province (14XW08).

Cite this paper

YujingLiu,LijunZhang,ShujingGao, (2016) An Improved Method to an Impulsive and Delayed Discretized Model. Applied Mathematics,07,108-123. doi: 10.4236/am.2016.71010

References