Applied Mathematics
Vol.06 No.03(2015), Article ID:54695,7 pages
10.4236/am.2015.63051
Programming First Integral Method General Formula for the Solving Linear and Nonlinear Equations
Mohamed A. Abdoon
Mathematics Department, Sudan University of Science and Technology, Khortom, Sudan
Email: moh.abdoon@gmail.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 February 2015; accepted 16 March 2015; published 17 March 2015
ABSTRACT
It’s well known that the solution of equations always uses complicated methods. In this paper the first integral method is used to find the actual solution of equations in a simple way, rather than the ex-complicated ways. Therefore, the use of first integral method makes the solution more available and easy to investigate behavior waves through its solution. First integral method is used to find exact solutions to the general formula and the applications of the results to the linear and nonlinear equations.
Keywords:
First Integral Method, Exact Solution, Linear and Nonlinear Equations

1. Introduction
Partial differential equations arise frequently in the formulation of fundamental laws of nature and in the mathematical analysis of a wide variety of problems in applied mathematics, mathematical physics, and engineering science. This subject plays a central role in modern mathematical sciences, especially in physics, geometry, and analysis. Many problems of physical interest are described by partial differential equations with appropriate initial and/or boundary conditions. These problems are usually formulated as initial-value problems, boundary- value problems, or initial boundary-value problems, a broad coverage of the essential standard material on linear partial differential equations and their applications is required. The study of the solutions of partial differential equations (PDEs) has enjoyed an intense period of activity over the last forty years from both theoretical and numerical points of view. Many methods obtaining the exact solution of non linear equation, some of the techniques are the bilinear transformation [1] , the sine cosine method [2] , F-expansion method [3] , the first integral method was first proposed by Feng [4] to solving Burger-Korteweg-devries equation and so on, in this paper investigation a traveling wave solution for non linear partial differential equation, study nonlinear phenomena, in solving modified KdV-kp can be based on the theory of commutative algebra, using the first integral method technique to solving linear and nonlinear equations.
2. First Integral Method
The non-linear partial differential equation form:
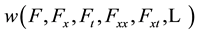 (1)
(1)
where 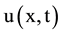 is the solution of (1) we use the transforms:
is the solution of (1) we use the transforms:
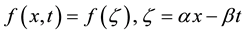 (2)
(2)
we use the wave transforms :
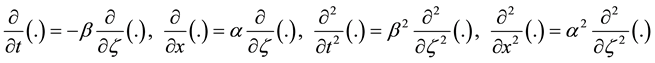 (3)
(3)
Equation (1) transforms the ordinary differential equations we obtain:
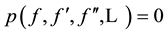 (4)
(4)
Anew independent variable:
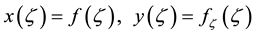 (5)
(5)
The system of ordinary differential equations:
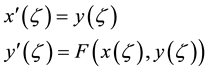 (6)
(6)
By the qualitative theory of differential equation [5] , we find the integral of (6) under same condition, then the general solution of (6) can be obtained directly. However, in general, it is really difficult for us to realize this even for one first integral, because for a given plane autonomous system, find its first integral will apply the Division theory to option first integral (6), An exact solution of (1) obtained by solving this equation. Now let us recall the Division theory.
Division theorem:
Suppose that 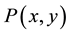 and
and 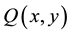 are polynomials of two variables
are polynomials of two variables 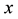 and
and 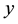 in
in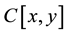 . And
. And 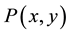 is irreducible in
is irreducible in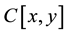 . If
. If 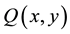 vanishes at all points of
vanishes at all points of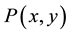 , then there exists a polynomial
, then there exists a polynomial 


3. The First Integral Method General Formula
We discuss the problem by using the first integral method, consider the general formula:

where 

Now Appling Division theorem, suppose that 


Is an irreducible polynomial in the complex domain 






which can be written as:

by comparing with the coefficient of 




from (12a), we deduce that 



Now we take these cases:
Case 1:
Suppose that M = 1, in (12), then the (13) becomes:



since 









where 


using (16) in (10), we obtain:

combining (17) with (8), and fine the exact solution (8).
Case 2:
Suppose that M = 2, in (12), then the (13) became:




since 










where 


using (20) in (9),we obtain two equal roots for Y:
note that:

combining (21) with (8), and fine the exact solution (8).
Case 3:
Suppose that M = 3, in (12), then the (13) became:





since 











where 
Substituting 

using (20) in (9), we obtain three equal roots for Y:
note that:
then

combining (21) with (8), and fine the exact solution (8).
Case n:
Suppose M = n, we get:

Theorem 3.1:
The exact solution of the general formula in (7) are given by combining of (17), (21), (27) … (29), with (8) and integration respect with
4. Application
We can apply Theorem 3.1 to studying some nonlinear differential equations, as solitary wave equation.
Example 4.1:
The linear ODES:

which is the same form of Equation (7), where:


integration respect to


so the (31) + (32) is the solution:
Example 4.2:
Consider the Boussines equation given by:

using 

where integrating twice yields:

which is the same form of (7), where:


integration respect to 

Example 4.3:
Consider the Gardner equation given by:

using the wave variable 

which is the same form of (7) where:

so:
integrating respect to 

Example 4.4:
Consider the nonlinear Schrödinger equation:

suppose that (46) has solution form:

substituting (47) in (46), then (46) become:

which is the same form of (48), where:


integrating respect to 

Example 4.5:
The Cahn-Allen equation: we study nonlinear parabolic PDF given by:

using the wave variable 

which is the same form of (48), where:



integrating respect to 




our result can be compared to Wawaz’s result [2] .
5. Conclusion
The first integral method a general formula, is successful for solving a lot of nonlinear equation, and establishing travelling wave solutions, which is based on the ring theory of commutative algebra, and used to solve complicated and tedious algebra calculation. We can also apply them to some other nonlinear partial differential equations.
References
- Hirota, R. (1980) Direct Method of Finding Exact Solutions of Nonlinear Evolution Equation. In: Bullongh, R. and Caudry, P., Eds., Backlund Transformation, Springer, Berlin, 115.
- Wazwaz, A.M. (2004) A Sine-Cosine Method for Handling Nonlinear Wave Equations. Mathematical and Computer Modelling, 40, 499-508.
- Zhou, Y.B., Wang, M.L. and Wang, Y.M. (2003) Periodic Wave Solutions to a Coupled KdV Equations with Variable Coefficients. Physics Letters A, 308, 31-36.
- Feng, Z.S. (2002) The First Integral Method to Study the Burgers-Korteweg-de Vriesequation. Journal of Physics A, 35, 343-349.
- Feng, Z. (2002) On Explicit Exact Solutions for the Lienard Equation and Its Applications. Physics Letters A, 293, 50-56. http://dx.doi.org/10.1016/S0375-9601(01)00823-4







