Advances in Bioscience and Biotechnology
Vol.4 No.4A(2013), Article ID:30632,6 pages DOI:10.4236/abb.2013.44A010
Theory of affinity maturation of antibodies
![]()
DRE-Dr. Riss Ellipsometerbau GmbH, Ratzeburg, Germany
Email: dr.riss@dre.de
Copyright © 2013 Udo Riss. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 17th, 2013; revised March 12th, 2013; accepted April 26th, 2013
Keywords: Affinity Maturation; Somatic Mutation; THz Waves; Antibody; Antigen
ABSTRACT
Based on the theory of long distance interaction between antibodies and antigens we developed a theory of affinity maturation of antibodies that is based on longitudinale electric waves. Early stage antibodies show a wide frequency spectrum for antigens and are polyspecific. After affinity maturation the antibody shows a very narrow band spectrum, the antibodies become monospecific. The feedback between antibody and antibody producing cell is done via messenger molecules that are also communicating with help of longitudinal electric waves. These messenger molecules transfer information from antibody arms and are informing cells whether the epitopes are switched on or off. The folding of antibody is done via eigen frequency resonances.
1. INTRODUCTION
The adaptive immune system produces antibodies, if for example antigens of viruses or bacteria are detected. At first polyspecific antibodies with low affinity are produced when the immune system recognizes the disease first time and then step by step the antibodies become monospecific [1] and the affinity of the produced antibodies increases. This process is defined as affinity maturation. In combination with somatic hypermutation of B-cells a process is started that leads to high affinity antibodies with high efficiency. At the moment there is no explanation existing that can explain stimulation of hypermutated B-cells. It is only known that activation-induced deaminase (AID) plays a role in this process [2].
Affinity of an antibody is caused by hyper variable binding loops. Each variable region of an antibody has 3 binding loops. Each binding loop is implemented in a given structure. Only length and sequence of the loops is changed for detection of different antigens [2]. The classical chemical theory of antibodies is based on the lock and key principle between antibody binding loops and antigen. But the binding loops consist of a beta-sheet and it is a question how the sequence and length of the binding loop can change the affinity to an antigen. Additional to this the structure of an antigen is not compatible to the structure of the antibody binding loops. To solve this problem the principle of induced fit is developed for antibody-antigen interaction [3]. This induced fit-process requires an external force that makes the induced fit. But no source for this force is known, a perpetuum mobile is not possible. And a second problem is that this force must work only for specific antibody antigen interactions. Our mathematical simulations showed that a specific force is required for the induced fit process, but specific forces are not known from other areas of physics, and so we have some doubt that a new specific force exists only for biological interaction. Symmetric bispecific antibodies [4] can also not be explained with the induced fit theory.
For a purely chemical interaction the binding/binning process between antibody and antigen must be in accordance with the law of mass action. But we found binning kinetics that is in contrast to the law of mass action. This was the reason for the development of our “Theory of long distance interaction between antibodies and antigens” [5]. Based on this theory we developed a theory for affinity maturation which will be presented in this paper. A better understanding of the process of affinity maturation will give a chance to produce high affinity antibodies in a bioreactor.
2. DIFFERENCE BETWEEN EARLY STAGE AND AFFINITY MATURATED ANTIBODIES
Figure 1 shows on the left side our model for an early stage antibody. The three binding loops (1…3) are represented by electric charged damped oscillators. Spectrum mathematics of damped oscillators is commonly known [6,7] and state of the art in physics. The structure of the

Figure 1. Early stage antibody (left side) and affinity maturated monospecific antibody after somatic mutation. Each binding loop of the early stage antibody is characterized by a damped electrical charged oscillator. The spectrum of field strength E of the longitudinal wave is shown under the mechanical block diagram of the antibody. In contrast to the early stage antibody has the affinity maturated antibody only a narrow band field strength spectrum.
high affinity antibody (Figure 1, right side) was already published [5] and calculated. In addition to this Figure 1 should demonstrate, that early stage antibodies are losing their dampers and that the number of springs reduces in the affinity maturation process.
The spectrum of each oscillator has wide bandwidth and the combination of the three spectra results in a wider bandwidth of the field strength spectrum of the antibody. The early stage antibody has low affinity and is polyspecific, if the immunsystem sees the disease for the first time. Affinity maturation in combination with hypersomatic mutation of B-cells leads to antibodies with narrow bandwidth and no damping of the three binding loop oscillators. All three oscillators are oscillating with the same frequency.
This type of antibody has high affinity and is monospecific which is perfect for therapeutic applications.
Antibody fragments are often produced with help of phage display techniques. But it is commonly known [8] that the produced antibody fragments are polyspecific. Changing the sequence of one of the binding loops of the heavy chain can increase the affinity to the target antigen. But doing this you can’t be sure that all binding loops show a field strength spectrum that is harmless for human body main functions. An attack to important body functions can be possible (Figure 2). Using phage dis-

Figure 2. Working with phage display it is possible that the produced antibody is also attacking an important body function (Red spectrum).
play for therapeutic antibody development is a stochastic try and error process which has a high risk. So it is possible that the created antibody acts like a highly specific poison.
For production of high affinity antibodies in a bioreactor it is important, that the process of affinity maturation and folding of antibodies is known completely and can be controlled in the bioreactor. To bring the process of affinity maturation and antibody folding to bioreactor technology the natural process must be understood.
To control the process of affinity maturation a feedback system from antibody to cell that has produced the antibodies is required. We think the immune system has such a feedback system.
3. FEEDBACK SYSTEM FROM ANTIBODY TO CELL
Each chain of an antibody has in the constant region an epitope and also an epitope in the variable region of the antibody chain [9]. Each epitope consists of charged and an uncharged amino acids. So the complete epitope is electrical charged. This charged epitope is oscillating and produces a longitudinal electric wave according to our theory of long distance interaction [5]. We think that epitopes are used for communication with other biological systems.
Figure 3 shows epitopes in the constant and variable region of an antibody arm. The epitopes are connected to the antibody chains via a disulfide bridge with high stiffness.
Disulfide bridges have a very high spring constant and so they are a stable reference point for the epitopes. The epitopes themself consist of amino acids, which have (compared to a disulfid bridge) significant lower spring constants. A molecules stroke from “Brownian Movement” brings via Dirac-pulse energy to an epitope so that it is possible that the epitope starts oscillating. We think epitopes are oscillating only in the transversal ground mode. An oscillating epitope produces a longitudinal electric wave that can be used for communication.
In the case of the antibody arms both chain epitopes are coupled by the corresponding antibody chain and so normally the energy would be transferred permanently from one epitope to next epitope of the chain and afterward back again. Only if the damping of both epitope oscillators is different there is no oscillation of the epitope that shows higher damping. This can be mathematically proven simply by adding damping to mathematics of our “theory of long distance interaction between antibodies and antigens” [5].
If the antibody searches an antigen the damping of the epitope in the variable region of the antibody is higher
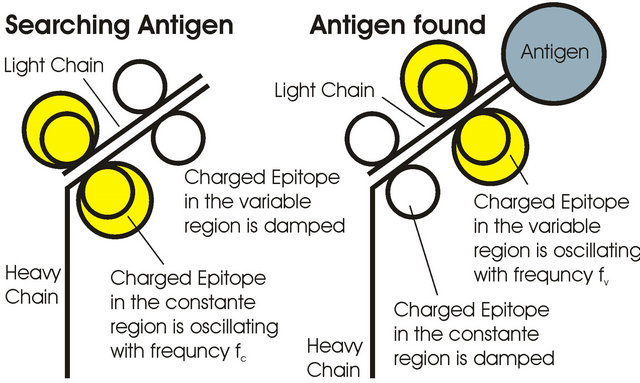
Figure 3. Antibody arm with oscillating epitopes (yellow). If the antibody is searching for an antigen the epitopes in the constant region of the chain are oscillating. Oscillation energy is transferred to the epitopes in the variable region, if an antigen is found.
and so only the antibody epitope in the constant region is oscillating with the frequency fc. This gives a feedback to the cell that the antibody is searching for an antigen. Has the antibody found an antigen the binding/binning process reduces the damping of the epitope that is in the variable region of the antibody chain. Now the epitope in the variable region is oscillating with frequency fv and gives the feedback to the B-cell that an antigen is found (the coupled epitope in the variable region stops oscillation). This information can be used for control of affinity maturation.
An oscillating epitope can be detected by another antibody and the binding/binning process that creates a sub-monolayer can be measured with an EL X-02B III or EL X-05BIII ellipsometer [10]. An epitope that is not oscillating can’t be detected by an antibody. It does not exist as antigenic determinant. According to our theory of long distance interaction between antibodies and antigens [5] only oscillating epitopes are antigens.
The problem in this concept is that the longitudinal wave that is produced by the epitopes has only low field strength and is absorbed by the surrounding medium (water). So signal transportation requires additional transmitter molecules that are amplifying the electric signals from the antibody arm epitopes.
The current theory says that messenger molecules are acting only on chemical basis. But we found for example no physical binding of Interleukin 4 to its target which was not expected in one of our ellipsometer experiments. And we further think that a chemical transport of information is too unsave and too slow for a feedback system between antibody and the producing cell, because messenger molecule movement is of stochastic nature.
So signal transportation must be on electrodynamic basis. This signal transportation acts with nearly light speed and is very save compared to a chemical signal transport.
Small molecules with alpha-helix structure show nonlinear spring characteristics [11]. Figure 4 shows the force-elongation diagram. In the range for small elongations this type of molecule has a small spring constant and high damping. Figure 5 shows the simplified mechanical model of this type of molecule. The spring constant c1 is very small; the spring constant c2 is higher. Figure 6a shows the force-elongation diagram of this two spring system. If this type of molecule is punched by parts of “Brownian Movement” a strongly damped oscillation of low frequency is started (Figure 6b) through a Dirac pulse. No information can be transported from the antibody epitopes to the cell because oscillation has wrong frequency and oscillation is damped.
This changes if the molecule sees an external electric longitudinal wave. This external wave forces the charge of the transmitter molecule over the range of spring c1. In

Figure 4. Force-elongation diagram of a nonlinear spring. The string characteristic is progressive.

Figure 5. Simplified mechanical model of a nonlinear messenger molecule. The spring c1 has small spring constant and high absorption d; the spring c2 has higher.
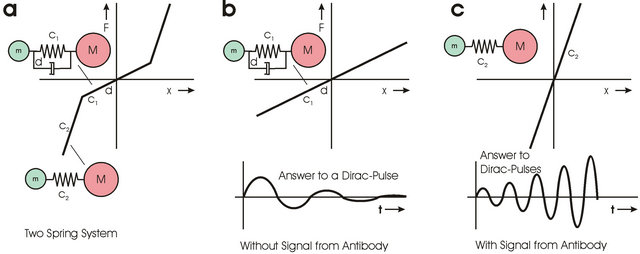
Figure 6. The left side a: shows a system with damping d and two spring constants c1 and c2. For small signals or Dirac pulses form “Brownian Movement” a disappearing low frequency oscillation is created that does not transport information; b: The Dirac pulse sees in this case the spring constant c1. This changes if the range in which the c1-spring is valid is bridged by an external electric field that forces the charge in the c1 range. The molecule oscillates now with high frequency. External Dirac pulses see now a spring with spring constant c2. This leads to amplification of the incident signal; c: The amplified signal has the same phase as the input signal coming from the antibody.
this case the oscillation frequency is defined by the frequency of the antibody epitope. Punching parts from “Brownian Movement” see the spring-elongation characteristic shown in Figure 6c. Dirac pulses from “Brownian Movement” lead now to amplification of the external signal. This effect is well known from classical mechanics (for example as resonance disaster).
The amplified signal produced by the messenger molecule is amplified by the next messenger molecule until the cell that controls the affinity maturation process is reached. The principle is similar to the principle of a cell phone that is communicating with an external antenna, which transports the signal to the next antenna until a second cell phone is reached.
A mathematical calculation of the simplified linearised two spring system is possible with classical methods of mechanics. Is the mass M significantly bigger than the charged mass m (Figure 5), the movement of the big mass M can be ignored, but it makes sense to add the spring mass between spring c1 and spring c2.
Messenger molecules that are able to transport information must have an alpha-helix (or a very long betasheet) structure inside. We think that both structures are simply nano-sized springs that have the task to realize electrodynamic oscillators in the THz-frequency range.
The feedback signals are used for affinity maturation of antibodies. We think the antibody producing cells are using a kind of successive approximation for optimizing of antibody affinity.
4. ALPHA-HELIX OR BETA-SHEET
We think that alpha-helix and beta-sheet structures simply act as mechanical spring. Messenger molecules require high nonlinearity and damping, so alpha helices are required. The binding loops of high affinity antibody require low nonlinearity and low damping. From mechanical point of view a beta-sheet is here the better choice. From spider silk it is known that beta-sheets have nearly linear spring characteristics [12].
5. FOLDING OF ANTIBODIES
The reason of antibody folding is not completely clear.
We think that the folding should produce structures that are able to oscillate. Different folding steps are possible to get a correctly folded molecule. So it is not important which structure is folded first, the result of the complete folding is important. Normally the amino acid structure defines the secondary structure. But there are also processes known where a structure is refolded from alpha-helix to beta sheet [13]. But in all cases we first have an alpha-helix or a beta-sheet which is in accordance with our theory a spring which builds together with a mass an electrical charged oscillator. Electrical shaking of such a structure with one of the eigen frequencies of the structure in the THz-frequency range will lead to a strong movement of the molecule structure which leads to the folding of the molecule. The molecule will arrange so that it can handle the external THz-field in the best form.
A similar effect is known from classical mechanics. If you put a flexible ferro fluid structure on a loud speaker and the frequency is identical with the eigen frequency of the local mechanical structure you will see a deformation of the flexible mechanical structure according to the eigen frequency [14].
We think that the folding process is controlled by the same simple mechanism. Shaking the unfolded antibody with the eigen frequencies of the binding loops and epitopes will lead to a correctly folded antibody. This implies refolding from alpha-helix structure to beta-sheet structure as it is already observed [13].
According to our theory a refold from alpha-helix to beta-sheet can take place if the external shaker frequency has a very narrow bandwidth. But in all cases the folding process is initiated from an alpha-helix or a beta sheet structure which build with masses and a charged oscillator.
Figure 7 shows such an electrodynamic shaker. Important is only that all eigen frequencies of an antibody must be used for shaking, otherwise the antibody will not be folded correctly.

Figure 7. Folding of an antibody by use of all eigen frequencies of the antibody.
We think that this process can be used in a bioreactor for correct folding of antibodies. But to get high affinity antibodies the bandwidth of the frequencies must be very small. A wide bandwidth produces polyspecific antibodies with low affinity, only a very small bandwidth will produce high affinity antibodies.
Only beta-sheets can be used as springs for creating high affinity shakers that can be used for high affinity antibody folding. According to our theory it must be possible to create antibodies with the same molecular sequences that have different affinities to slightly different antigens simply by modifying the folding frequentcies.
The folding process is in principal mathematical calculable with a kind of finite element program. If nonlinear mechanical spring constants of all amino acids are known and all binding effects of all amino acid combinations are known it must be possible to calculate the result of the folding process. But the way to correct folded antibody can be different.
6. PROOF OF THEORY
This is a theory that is based on measurement experience, but it still must be proven. Possible experiments are described below.
The theory states that antibody arm epitopes are switched on and off in dependence of the antibody status (bound/unbound to an antigen). If antibodies are searching for an antigen other antibodies can bind to definite antibody arm epitopes. A binding/binning to these antibody arm epitopes changes significantly if the antibodies themselves have bound to an antigen.
Antibodies can also bind to messenger molecules; if the antibodies that are belonging to the antibody arms are in the neighborhood. The affinity to the messenger molecules reduces if no antibodies are in the neighborhood of the messenger molecules.
The proof of the folding theory is a challenge, but from theory it must be possible to influence the folding process by use of high specific antibodies or messenger molecules, which are in the neighborhood of the unfolded molecule, when folding takes place.
We think the plaque produced by wrong (beta sheet) folding of proteins to prions is not the primary reason for Alzheimer disease. According to our theory Alzheimer is caused by missing of two channel messenger molecules (proteins) with correct folded alpha-helices. But a big number of wrong folded proteins (prions) that are in the neighborhood of the molecular folding machines for proteins effect the folding process with their electrodynamic field und lead to further wrong folded proteins (prions). This increases the lack of correct folded messenger proteins.
7. SUMMARY AND OUTLOOK
The above work uses knowledge that is state of the art in other disciplines.
Longitudinal waves are defined in Maxwell’s equations as current density and/or change of charge displacement. Maxwell’s equations themself are based on the laws of mechanics.
The laws of mechanics are well known in mechanical engineering and physics. They are valid for big machines and atomic structures. In additional to this, we have made measurements with an ellipsometer to get knowledge on the behavior of biological molecules.
The task of this work is to make it possible “in future” to produce therapeutic antibodies in a bioreactor. After producing the amino-acid sequence of an antibody in a first process, the building of the secondary structures (alpha-helices or beta-sheets) will take place automatically in a second step. Then the folding must be done separately in a third step.
REFERENCES
- Riss, U. (2012) Theory and measurement of long distance interaction between antibodies and antigens. Bit’s 4th Annual Congress of Antibodies, Peking, 2012, 29.
- Alberts, B., Johnson, A., Lewis, J., Raff, M., Roberts, H. and Walter, P. (2011) Molekularbiologie der Zelle. WileyVCH Verklag GmbH & Co. KGaA, Weinheim.
- Rini, J.M., Schulze-Gahmen, U. and Wilson, I.A. (1992) Structural evidence for induced fit as a mechanism for antibody-antigen recognition. Science, 255, 959-965. doi:10.1126/science.1546293
- Yan, C. (2012) Generation and affinity maturation of fully human soluble VH domain antibodies and IgGs using dsDNA display. Bit’s 4th Annual Congress of Antibodies, Peking, 26-28 March 2012, 59.
- Riss, U. (2011) Theory of long distance interaction between antibodies and antigens. European Biophysics Journal, 40, 987-1005.
- Trevor King, W. (2009) Theoretical power spectral density for a damped harmonic oscillator. http://www.physics.drexel.edu/~wking/rsrch/papers/cantilever_calib/node3.html
- http://users-phys.au.dk/hans/tidsserie/Notes_05.pdf
- Riss, U. (2012) Theory and measurement of long distance interaction between antibodies and antigens. Bit’s 4th Annual Congress of Antibodies, Peking, 2012, 29. (Information received after discussion)
- Hans Martin Jäck (2007) Konzepte der immunologie für naturwissenschaftler. Leture Notes, University Erlangen, Erlangen. http://www.molim.uni-erlangen.de/docs/konzepte_ak_methoden.pdf
- Riss, U. (2013) Error corrected sub-monolayer ellipsometry for measurement of biomolecular interactions. Open Journal of Biophysics, 3, 76-85. doi:10.4236/ojbiphy.2013.31A010
- Idris, A., Alam, M.T. and Ikai, A. (2000) Spring mechanics of alpha-helical polypeptide. Protein Engineering Design and Selection, 13, 763-770. doi:10.1093/protein/13.11.763
- http://en.wikipedia.org/wiki/Spider_silk
- Gross, M. (2000) Proteins that convert from alpha helix to beta sheet: Implications for folding and disease. Current Protein & Peptide Science, 1, 339-347. doi:10.2174/1389203003381289
- You Tube Video (2008) Non-Newtonian fluid on a speaker cone. http://www.youtube.com/watch?v=3zoTKXXNQIU

