International Journal of Astronomy and Astrophysics
Vol.06 No.03(2016), Article ID:70745,6 pages
10.4236/ijaa.2016.63027
Change in Internal Energy and Enthalpy of Spinning Black Hole with Half Spin Parameter in XRBs
Dipo Mahto1, Amresh Kumar Singh2, Niharika Kumari2
1Department of Physics, Marwari College Bhagalpur, T. M. B. University, Bhagalpur, India
2Department of Physics, T. M. B. University, Bhagalpur, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 July 2016; accepted 18 September 2016; published 21 September 2016
ABSTRACT
Mahto et al. gave an expression for the change in enthalpy and internal energy with corresponding change in the radius of the event horizon of black holes of spin parameter a* = 1 (2013). On the basis of this research work, we have proposed an expression for the change in the internal energy and enthalpy of the spinning black holes to assume spin parameter a* = 1/2 and calculated their values for different test spinning black holes existing in XRBs.
Keywords:
Enthalpy, Spinning Black Holes, Internal Energy

1. Introduction
Classically, the black holes are perfect absorbers and do not emit anything; their temperature is absolute zero. However, in quantum theory black holes emit Hawking radiation with a perfect thermal spectrum. This allows a consistent interpretation of the laws of black hole mechanics as physically corresponding to the ordinary laws of thermodynamics [1] . Kumari et al. have derived the formula for the energy of non-spinning black holes (EBH) in terms of the radius of the event horizon [2] . According to the theory of relativity, a black hole is the solution of Einstein’s gravitational field equations in the absence of matter that describes the space time around a gravitationally collapsed star and its gravitational pull strong that even light can not escape from it [3] . Mahto et al. have derived the formula for the change in energy of non-spinning black holes (BHs) due to corresponding change in radius of the event horizon [4] . Mahto et al. derived also an expression for the change in entropy of Non-spinning black holes using the first law of the black hole mechanics relating the change in mass M, angular momentum J, horizon area A and charge Q, of a stationary black hole [5] . Mahto et al. proposed a model for the change in enthalpy and internal energy with corresponding change in the radius of the event horizon of black holes with spin parameter a* = 1 [6] .
In the present paper, we have proposed an expression for the change in the internal energy and enthalpy of the spinning black holes to assume spin parameter a* = 1/2 on the basis of research work [6] .
2. Discussion
The change in internal energy and enthalpy of black holes with corresponding change in the radius of the event horizon of black holes is given by [6] ,
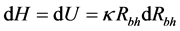 (1)
(1)
In the case of spinning black holes, the change in internal energy will have different values than that of non-spinning black holes, because in this case, the surface gravity of a black hole is given by the Kerr solution [1] .
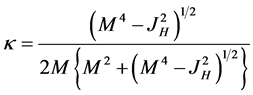 (2)
(2)
where
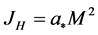 (3)
(3)
The radius is smaller in the case of spinning black holes, tending to GM/c2 as a* tends to 1 [7] and in the case of spinning black holes having spin parameter (a* = 1/2), then we have,
where
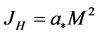 (4)
(4)
hence
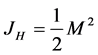 (5)
(5)
or
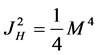 (6)
(6)
we have
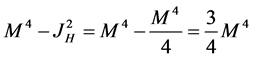 (7)
(7)
or
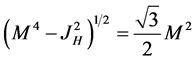 (8)
(8)
or
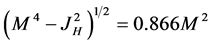 (9)
(9)
or
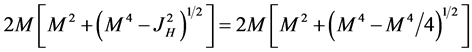 (10)
(10)
or
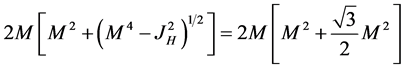 (11)
(11)
or
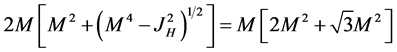 (12)
(12)
or
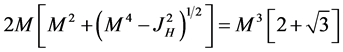 (13)
(13)
or
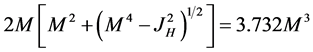 (14)
(14)
Putting the Equations ((9) and (14)) into (2) and solving, we have
 (15)
(15)
Putting the above value in Equation (1) becomes

For negligible change in the radius of the event horizon, the radius of the event horizon (Rbh) can be used instead of 

The above equation shows the change in enthalpy/internal energy of spinning black holes with spin 1/2 and may be used to calculate their values for given mass and corresponding radius of event horizon in XRBs.
The Equation (17) can be written as:
For the spherically symmetric and stationary or Schwarzschild black hole’s mass M, the horizon’s radius is

Using the Equation (18) into the Equation (17) and solving, we have

The standard Bekenstein entropy is given by the following expression [9]

Using the Equation (20) into the Equation (19) and solving, we have

For constant mass of the black hole, the change in enthalpy/internal energy is directly proportional to the surface area of event horizon (entropy) of black hole. The Equations ((19) and (21)) justify the uniform variation between the change in enthalpy/internal energy and the surface area of event horizon (entropy) of the black hole.
3. Data in the Support for Mass of Black Holes
There are two categories of black holes classified on the basis of their masses clearly very distinct from each other, with very different masses M ~ 5 20 Mʘ for stellar-mass Black holes in X-ray binaries and M ~ 106 - 109.5 Mʘ for super massive black holes in Active Galactic Nuclei [4] [7] . Mass of sun (Mʘ) = 1.99 ´ 1030 kg, [7] .
4. Result and Discussion
On the basis of the data mentioned above regarding the mass of sun and black holes in XRBs, we have calculated change in internal energy and enthalpy of spinning black holes in XRBs for given radius of event horizon and corresponding mass of different test spinning black holes of spin parameter a* = 1/2, listed in the Table 1.

and then calculated their values of different test spinning black holes existing in XRBs. The above equation is extended in terms of the surface area of event horizon, A and entropy, S of the spinning black hole which shows the dependence of the change in enthalpy/internal energy on the surface area of event horizon and entropy of black hole. To understand clearly the change in enthalpy as well as change in internal energy, the graph has been plotted between the radius of event horizon and corresponding change in the enthalpy/internal energy of spinning black holes with spin (
From the observation of the data in the table, it is clear that the change in enthalpy as well as internal energy of different test spinning black holes increases with increase in corresponding change in values of the mass/radius of the event horizon in XRBs. From the observation of the graph in the Figure 1, it is clear that the change in enthalpy of different test spinning black holes increases linearly with increase in corresponding change in values of the mass/radius of the event horizon in XRBs. The nature of the graph plotted between the change in the radius of event horizon of different test spinning black holes & their corresponding change in internal energy in XRBs will be also in a straight line (not shown in figure because of the same data). The graph plotted between the change in radius of event horizon of different test spinning black holes & their corresponding change in enthalpy as well as internal energy in XRBs is a straight line showing the uniform variation in enthalpy as well as internal energy with corresponding values of surface area of the black hole horizon (entropy) of spinning black holes as clear from Equations ((19) and (21)). The straight line also shows that there is a definite relation between the mass/event horizon of spinning black holes and change in enthalpy as well as internal energy and gives the validity for both the (16) and (17).
The graph plotted in Figure 1 has the same nature as the graph plotted between the radius of event horizon (Rbh) of different test black holes and their corresponding entropy change w.r.t. the change in event horizon
Table 1. The change in enthalpy/internal energy of spinning black holes in XRBs.
Figure 1. The graph plotted betn the event horizon &corresponding change in enthalpy of the spinning BHs.
(δSbh/Rbh) in XRBs using the relation of entropy change given by 
5. Conclusion
In course of the present research work, we can draw the following conclusions such as:
1) The spinning black holes with spin (
2) There is no change in internal energy entropy and enthalpy in the case of spinning black holes having spin equals to (
3) For max. spin (
4) The change in entropy and enthalpy have the same nature for spinning black holes with half spin parameter.
5) There is uniform variation in the change in enthalpy (dH) and internal energy (dU) with change in surface area of event horizon for different types of spinning black hole candidates in XBRs showing definite relation between the surface area of event horizon and change in enthalpy as well as internal energy.
Cite this paper
Dipo Mahto,Amresh Kumar Singh,Niharika Kumari, (2016) Change in Internal Energy and Enthalpy of Spinning Black Hole with Half Spin Parameter in XRBs. International Journal of Astronomy and Astrophysics,06,328-333. doi: 10.4236/ijaa.2016.63027
References
- 1. Bardeen, J.M., Carter, B. and Hawking, S.W. (1973) The Four Laws of Black Hole Mechanics. Communications in Mathematical Physics, 31, 161-170.
http://projectuclid.org/euclid.cmp/1103858973
http://dx.doi.org/10.1007/BF01645742 - 2. Nozari, K. and Fazlpour, B. (2008) Reissner-Nordstrom Black Hole Thermodynamics in Non-Commutative Spaces. Acta Phys. Pol. B, 6, 39.
- 3. Bekenstein, J.D. (2008) Bekenstein-Hawking Entropy. Scholarpedia, 3, 7375.
- 4. Narayan, R. (2005) Black Holes in Astrophysics. arXiv:gr-qc/0506078v1.
- 5. Mahto D., Singh, A.K., Ram, M. and Vineeta, K. (2013) Change in Internal Energy & Enthalpy of the Black Holes. International Journal of Astrophysics and Space Science, 1, 20-22.
http://dx.doi.org/10.11648/j.ijass.20130104.12 - 6. Mahto, D, Prakash, V., Prasad, U., et al. (2013) Change in Entropy of Non-Spinning Black Holes w.r.t. the Radius of Event horizon in XRBs. Astrophysics and Space Science, 343, 153-159.
- 7. Mahto, D., Kumari, K., Sah, R.K., et al. (2012) Study of Non-Spinning Black Holes with Reference to the Change in Energy and Entropy. Astrophysics and Space Science, 337, 685-691.
http://dx.doi.org/10.1007/s10509-011-0883-7 - 8. Dabholkar, A. (2005) Black Hole Entropy in String Theory—A Window in to the Quantum Structure of Gravity. Current Science, 89, 25.
- 9. Kumari , K., Mahto, D., Chandra, G., et al. (2010) Study of Schwarzschild Radius with Reference to the Non-Spinning Black Holes. Bulletin of Pure and Applied Sciences, 29D, 183-187.




