Open Journal of Statistics
Vol.04 No.11(2014), Article ID:52865,21 pages
10.4236/ojs.2014.411092
A Measure for Assessing Functions of Time-Varying Effects in Survival Analysis
Anika Buchholz1, Willi Sauerbrei1, Patrick Royston2
1Center for Medical Biometry and Medical Informatics, Medical Center - University of Freiburg, Freiburg, Germany
2MRC Clinical Trials Unit at University College London, London, UK
Email: ab@imbi.uni-freiburg.de, wfs@imbi.uni-freiburg.de, j.royston@ucl.ac.uk
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 30 September 2014; revised 25 October 2014; accepted 18 November 2014
ABSTRACT
A standard approach for analyses of survival data is the Cox proportional hazards model. It assumes that covariate effects are constant over time, i.e. that the hazards are proportional. With longer follow-up times, though, the effect of a variable often gets weaker and the proportional hazards (PH) assumption is violated. In the last years, several approaches have been proposed to detect and model such time-varying effects. However, comparison and evaluation of the various approaches is difficult. A suitable measure is needed that quantifies the difference between time- varying effects and enables judgement about which method is best, i.e. which estimate is closest to the true effect. In this paper we adapt a measure proposed for the area between smoothed curves of exposure to time-varying effects. This measure is based on the weighted area between curves of time-varying effects relative to the area under a reference function that represents the true effect. We introduce several weighting schemes and demonstrate the application and performance of this new measure in a real-life data set and a simulation study.
Keywords:
Cox Model, Measure of Distance, Survival Analysis, Time-Varying Effects

1. Introduction
The Cox proportional hazards model [1] is the standard approach for modelling time to event data. In some applications, though, especially with large sample sizes and/or long follow-up, the proportional hazards (PH) assumption may be violated. One reason for non-PH is that effects of covariates change over time. Ignoring this time-varying behaviour, i.e. modelling constant effects, results in incorrect models and possibly false conclu- sions thereof.
The first proposal for an extension of the Cox model is given by Cox [1] in his original paper. He proposed to introduce time-dependent components 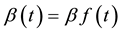 based on a pre-defined parametric function of time
based on a pre-defined parametric function of time 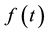 in case of non-PH. However, as the shape of the estimated time-varying effect is determined by the specified function, an inappropriate choice of
in case of non-PH. However, as the shape of the estimated time-varying effect is determined by the specified function, an inappropriate choice of 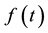 may lead to incorrect interpretation of results. Often, smoothed scaled Schoenfeld residuals [2] are used to gain an impression of the shape of
may lead to incorrect interpretation of results. Often, smoothed scaled Schoenfeld residuals [2] are used to gain an impression of the shape of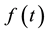 . Another popular technique is partitioning of the time axis, also called piecewise constant effects. Based on the idea that the PH assumption holds at least over short time periods, separate effects are fitted for each period (under the PH assumption) resulting in a step-function for
. Another popular technique is partitioning of the time axis, also called piecewise constant effects. Based on the idea that the PH assumption holds at least over short time periods, separate effects are fitted for each period (under the PH assumption) resulting in a step-function for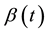 . Yet, the number and position of jump times is crucial and may severely influence the estimated effects.
. Yet, the number and position of jump times is crucial and may severely influence the estimated effects.
In the last years, several more sophisticated approaches have been proposed. The variety of underlying techniques for modelling time-varying effects among these approaches is broad. They include splines [3] [4] , non-parametric techniques [5] and fractional polynomials [6] [7] . When using different approaches for modell- ing time-varying effects, one may end up with estimates of various types, i.e. interval wise (constant) estimates, piecewise polynomials (often only evaluated at specific time points) or functional forms depending on time. The broad variety of methods makes a comparison of different approaches complex and judgement about which approach is best, i.e. most similar to the true effect, is difficult.
In a Cox model the PH assumption is often acceptable for several variables, but may be critical for some of them. Plotting scaled Schoenfeld residuals [2] from a model is a popular technique to assess whether the effect of a specific variable varies in time. A plot of residuals plus estimated function (termed SSSRs) against time reflects the raw data. A smoother through SSSRs points toward the true shape of the effect in time [8] using the so far unexplained variation. An important issue is the amount of roughness. We propose to use a very rough smoother through SSSRs to represent the unknown truth (gold standard) and quantify the difference of an estimated function to this truth. However, for an effect varying in time such a smoother can only be presented as a plot. When investigating a single data set, this graphical approach can be used to compare different time- varying estimates, although graphs with wiggly functions are usually less helpful to understand, report and transport the results with the clinical message [9] . In simulation studies or bootstrap based analyses, though, graphical analyses are not feasible any more.
In addition, direct comparison between the different approaches does not answer the question about which one is best. To get an answer to this question, we have to evaluate the similarity of either approach to the truth (e.g. the true effect in simulations or the SSSRs in real data). This stresses the need for a quantitative measure of the difference between the truth and the estimated function(s) under investigation.
For time-varying effects, we propose to adapt the technique for quantifying the area between smoothed curves proposed by Govindarajulu et al. [10] . This adapted measure, the area between curves for time-varying effects (ABCtime), quantifies the distance between two curves of estimated effects and weights the distances according to an appropriate weighting scheme which may reflect the importance of specific time intervals. Most relevant are situations where one of the curves is the truth (in a simulation study) or a rough smoother through SSSRs, the latter being a substitute for the truth in real data.
In Section 2 we briefly introduce two approaches for modelling time-varying effects, which are used for illustrating purposes. The ABCtime measure itself is presented in Section 3. In Section 4 we introduce a real data example and a simulation study, followed by an illustration of the use of ABCtime in these examples (Section 5) and a discussion (Section 6).
2. Background: Time-Varying Effects in an Extended Cox Model
2.1. The Standard Cox Proportional Hazards Model
The Cox proportional hazards model [1]
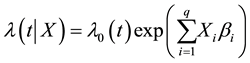
is the standard tool in survival analysis. In some situations, though, the proportional hazards (PH) assumption may be violated due to the presence of time-varying effects. A potential violation of the PH assumption is often explored based on the Schoenfeld residuals [2] . Plotting the scaled Schoenfeld residuals plus 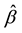 against time, or some function of time
against time, or some function of time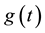 , can reveal the shape of the time-varying effect [8] . This method reflects the “raw data” and can give an impression of the true effect. Hence, it can be used as a reference to evaluate estimated time-varying effects. However, SSSRs raise the question of a suitable smoother and amount of rough- ness.
, can reveal the shape of the time-varying effect [8] . This method reflects the “raw data” and can give an impression of the true effect. Hence, it can be used as a reference to evaluate estimated time-varying effects. However, SSSRs raise the question of a suitable smoother and amount of rough- ness.
They shall reflect the true time-varying behaviour of effects and thus should be flexible enough to reflect the underlying time-varying shape including possible short-term changes, but on the contrary should not be too
noisy. Therefore, we chose a symmetric nearest neighbour smoother with a span of 0.75, i.e. 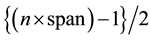 nearest neighbours on each side of the smoothed point are used, where
nearest neighbours on each side of the smoothed point are used, where 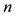 is the number of observations.
is the number of observations.
2.2. The Fractional Polynomial Time Approach
The Fractional Polynomial Time (FPT) approach is part of the Multivariable Fractional Polynomial Time (MFPT) algorithm [7] , which combines variable selection with selection of functional forms of covariates (MFP algorithm) and selection of time-varying effects (FPT algorithm). Hence, MFPT results in a model of type
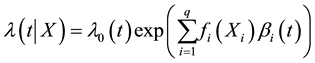
with potentially non-linear functional forms of covariates 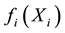 and time-varying effects
and time-varying effects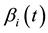 .
.
FPT is the part of MFPT which focuses on the selection of a time-varying effect for one covariate using a function selection procedure based on fractional polynomials [11] . The polynomial power terms are defined by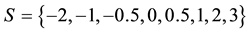 , with the non-standard definition
, with the non-standard definition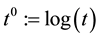 . With this set of powers, eight fractional polynomials of degree 1 (FPT1) and
. With this set of powers, eight fractional polynomials of degree 1 (FPT1) and 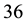 fractional polynomials (FPs) of degree 2 (FPT2) are com- pared for each variable based on deviance differences.
fractional polynomials (FPs) of degree 2 (FPT2) are com- pared for each variable based on deviance differences.
A time-varying effect based on an FPT1 is of type

There are many examples showing that the time-varying effect decays over time and the log transformation is often used successfully to estimate the functional form. In the FPT algorithm it is used as the default function for a variable with a time-varying effect.
To select a time-varying effect, a hierarchical closed test procedure based on deviance differences is applied:
1) Test the best-fitting FPT2 function 
2) Test 

3) Test 
2.3. Semiparametric Extended Cox Model
Scheike and Martinussen [5] proposed the Semiparametric Extended Cox model (in the sequel denoted by Timecox) based on cumulative parameter functions, which has been developed mainly for testing on time- varying effects.
In multivariable analyses, they recommend to start with the fully non-parametric model [5] , where all covariate effects are allowed to vary with time, and then simplify it based on a Kolmogorov-Smirnov type test in a backward elimination manner to a semiparametric model, where only some covariate effects vary with time while others are assumed to be constant:
where 


Estimation and tests are based on the cumulative regression functions
as they are consistent and converge at a faster rate than 


The test on a time-varying effect for covariate 


where 


3. The Area between Curves
The area between two curves can be used to quantify the distance between these curves. Depending on the application, this technique may be adapted and the area may be weighted according to the specific requirements.
3.1. Smoothed Curves in Regression Models
Govindarajulu et al. [10] proposed a method to measure the distance between smoothed curves. They calculate the area between the curves based on the idea of numerical integration. The area under a curve is estimated using 500 successive non-overlapping rectangles with equal width. The height of each rectangle is determined by the right endpoint of the interval. Summing up the area of all rectangles gives the area under the curve. To determine the area between two curves 



precision in the estimates across the range of exposure, Govindarajulu et al. [10] calculate the area between the curves as a weighted difference. The weights 

where 


25 to 200 bootstrap samples will usually be needed to obtain a reasonable estimate of variance [12] , Govindara-
Figure 1. Area between the curves for regression models according to Govindarajulu et al. [10] (left) and adapted for time-varying effects (right). The former determines the height of rectangles based on the right endpoint of intervals, while the latter uses the midpoint.
julu et al. [10] used 50 bootstrap samples. Assuming that 



The area difference is then calculated as
and 

To assess how close two curves are, the area difference between the curves is presented as percent of the average area under the two curves. Consequently, the closer the curves, the smaller the percentage.
3.2. Curves for Time-Varying Effects
The concept of the area between curves is not restricted to smoothed curves of exposure but is applicable to a wider range of functions as, for example, time-varying effects. Transfer to this setting, though, requires some modifications of the original method proposed by Govindarajulu et al. [10] .
3.2.1. Requirements on Flexibility
The variety of different approaches proposed for modelling time-varying effects is broad, ranging from explicit functional forms for time-varying effects to estimates that are available only at certain specified time points or as step-functions [13] . One method providing an explicit and simple functional form for the estimated time-varying effects are fractional polynomials as used, for example, in the FPT approach. Yet, there are some other appro- aches (e.g. based on splines or other complex modelling techniques) for which, although theoretically (complex) functional forms for the estimated time-varying effects are available, software programs only provide function values at specific time points. Thus, in practice one would construct a step-function out of these values to obtain a functional form (or take the effort to try reconstructing the complex functional form of the estimates). Another technique providing a step-function is partitioning of the time axis, also called piecewise constant effects. This method is based on the idea that the PH assumption holds at least over short time periods and fits separate effects for each period (under the PH assumption), thus resulting in a step-function for the time-varying effect
Hence, ABCtime should be applicable to continuous functions, as well as to right- and left-continuous step functions to cover the broad variety of potential approaches for modelling time-varying effects. Consequently, using the left endpoint of intervals for calculation of ABCtime may lead to biased results. If the left endpoint for an ABCtime rectangle is identical to the left endpoint of a left-continuous step function, the “wrong” function value will be used. The same applies for right-continuous step functions and the right endpoint. Hence, the middle of the intervals is the best choice in this situation to avoid systematic use of “wrong” function values (see Figure 1).
3.2.2. Choice of Weights
Govindarajulu et al. [10] had used bootstrap sampling to obtain the variance of the height of rectangles to account for the varying precision in the estimates of the relative risk across the range of exposure. However, the change in precision can be accounted for in different ways and in case of time-varying effects some reasonable alternatives exist.
In addition, the focus of the individual analysis may also influence the preferences about the weights. Yet, the choice of weights is rather subjective and dispensing with a bootstrap component in the weights speeds up calculation of ABCtime considerably. Especially with computer-intensive approaches and/or in simulation studies, we favour simple non-bootstrap alternatives.
An unweighted version, i.e. equal weights 

with 
Alternatively, the weights could be based on the inverse mean variance of the competitive approaches. If 
where 

Other possibilities would be to use weights based on the number of patients at risk. Weights based on the number of patients at risk (i.e. logrank like weights)
reflect the importance of deviations in the time-varying effects over time. Here, 

3.2.3. Restriction of Time Range
A potential drawback of variance based weighting schemes (e.g.
Analogously, the evaluation period for ABCtime has to be chosen with care. It is often sensible to focus on a relevant region or a region of interest by restricting the calculation of ABCtime to the time range


3.2.4. Calculation of ABCtime and pABCtime
The ABCtime is then calculated in the style of Equation (12) in Govindarajulu et al. [10] as
with 


To improve interpretation of the values of ABCtime, we further calculate the percentage of ABCtime on the weighted area under the reference function (termed pABCtime):
where the area under the reference curve (AUR) is calculated in analogy to ABCtime as the (weighted) area between the reference curve and the 

Although we argue for simple weights for calculation of ABCtime itself, we will in the sequel use bootstrap techniques to assess the stability of this measure. For this purpose, we calculate the standard deviation and 95% bootstrap percentile intervals based on the pABCtime values calculated in bootstrap samples. All functions under investigation are reestimated in 

4. Data
This chapter introduces the real-life data set and the simulated data that are in the sequel used to demonrate the application of ABCtime. Here, we restrict investigation to univariate settings. However, all techniques can be applied to multivariable settings analogously.
4.1. Rotterdam Breast Cancer Series
The Rotterdam breast cancer series includes data on patients treated at the Erasmus MC Daniel den Hoed Cancer Center for primary breast cancer between 1978 and 1993 [7] [15] . Data from 2982 patients are available for analysis. For details on selection criteria and exclusions, see [7] . Follow-up time ranges from 1 to 231 months (median 107 months, reverse Kaplan-Meier method). The endpoint event-free survival time (EFS) is defined as time from primary surgery to the first occurrence of locoregional or distant recurrence, contralateral tumour, secondary tumour or death from breast cancer. Times to death from other causes are treated as censored. With this outcome, 1518 events are observed. To avoid potential distortion of time-varying effects, we censor the data at 10 years, leaving 1477 events for analysis.
Sauerbrei, Royston and Look [7] identified eight prognostic factors with an important influence on EFS (model M1), thereof two with a non-linear effect. Investigation of the Schoenfeld residuals for these variables reveals some potential time-varying effects (see Figure C1 and Table C1 in the Appendix). To keep the example simple, we concentrate on univariate investigation of the hormonal therapy and the transformed number of lymph nodes

4.2. Simulated Data
To investigate the performance of the ABCtime method in a setting where the truth is known, simple data sets with one variable are generated. Survival times are simulated using a generalised inversion method (see [16] , Chap. 6.2 for more details) with administrative censoring to avoid potential problems caused by sparse data at the end of follow-up (resulting in about 41% - 52% censored observations). We consider two different shapes of effects: a linearly 

5. Results
To illustrate the use of the ABCtime measure, we apply it to the CoxPH, FPT, and Timecox models in the Rotterdam breast cancer series and the simulated data. Time-varying effects are selected with a conservative significance level of

5.1. Rotterdam Breast Cancer Series
5.1.1. Number of Positive Lymph Nodes


using pABCtime. The restricted period used for the calculation of pABCtime is from about 3 months to 9.7 years in this data set.
Figure 2 shows the SSSRs (reference) and their pointwise 95% confidence intervals, as well as the estimated CoxPH, FPT and Timecox effects for
The basis for calculation of ABCtime is the area difference between the SSSRs and the CoxPH, FPT and Timecox effects, respectively, as shown in Figure 3. The ABCtime is calculated as a weighted (or unweighted) sum of these area differences. The area differences already suggest that, as expected, Timecox and FPT are closer to the reference SSSR curve than the time-constant CoxPH effect, but the difference between the two of them is small.
Figure 4 shows the pABCtime for 
The influence of the different weights on the pABCtime can most easily be demonstrated by the CoxPH results. While in the unweighted version (i.e. with equal weights) the weights, of course, remain constant over the complete observation period, the weights in the three other weighting schemes change with calculation
Figure 2. Rotterdam,
Figure 3. Rotterdam,
Figure 4. Rotterdam,




intervals of ABCtime, i.e. each rectangle 
Similar tendencies can be observed for the FPT and Timecox effects. Yet, they are less pronounced in this example, since both estimates are very similar to the SSSRs and the pABCtime is relatively small with 4.5 and 6.2 for FPT and Timecox, respectively, in the original data and up to about 20% for both in the bootstrap samples. CoxPH on the contrary showed pABCtime values of 21.6 and up to 40 in the original data and boot- strap samples, respectively. These small values are caused mainly by a large AUR, i.e. a rather large effect size. In comparison to this effect size, differences between the estimated effects and the SSSRs are relatively small which is reflected by a small pABCtime (i.e. percentaged difference relative to the AUR).
According to a visual comparison of the effect estimates obtained by FPT and Timecox in the original data (Figure 2 and Figure 3), both estimates reflect the shape of the SSSRs (i.e. the reference function) similarly well. Yet, the more flexible Timecox estimate shows a local pattern between the years 2 and 5, which however is not clearly indicated by the SSSRs and also does not lead to a reduction in pABCtime. In contrast, FPT tends to yield slightly smaller values of pABCtime than Timecox, i.e. it is slightly more similar to the reference in the original data and over the bootstrap samples.
Thus, pABCtime provides a straight-forward quantification of the similarity to the reference curve, which is often hard to evaluate using graphical displays only (e.g. in simulation studies). In addition, pABCtime measurements in the individual bootstrap samples and corresponding bootstrap percentile intervals enable evaluation of variability/stability of effect estimates in real-life data sets. For 
A striking pattern in Figure 4 is that for FPT and Timecox the pABCtime in the original data is smaller than the mean over bootstrap samples. This is due to the fact that in the bootstrap samples there is more often a larger difference between the estimated effects and the SSSRs, either due to a deviating functional form of the effect estimate, artefacts or fluctuations in the SSSRs themselves. Thus, the bootstrap percentile intervals of pABCtime also reflect the sensitivity of effect estimates (e.g. artefacts or “strange” shapes) obtained by the different ap- proaches to slight changes in the data.
5.1.2. Hormonal Therapy
Although in a multivariable context the proportional hazards assumption seems questionable for the hormonal therapy (see Figure C1 and Table C1 in the Appendix), it may be acceptable in the univariate context (Figure C2). Here, all three approaches estimate virtually identical time-constant effects. This is reflected well in the pABCtime, which is also nearly identical, independent of the weighting scheme used (Table C2). Yet, the three approaches differ in terms of the 95% bootstrap percentile intervals, i.e. the stability of effect estimates. While the percentile intervals of CoxPH and FPT are similar, the Timecox procedure shows a considerably increased upper limit. A closer look at the boxplots of pABCtime over all bootstrap samples shows several outliers for both FPT and Timecox, but more pronounced for the latter (Figure C3). These are mostly bootstrap replications in which time-varying effects have been selected, thus resulting in larger differences to the nearly constant reference (Figure C4). Hence, the additional information on the stability of estimated effects obtained from the bootstrap percentile intervals and boxplots of pABCtime aids in deciding for the most suitable approach also w.r.t. potential sensitivity to artefacts in estimated effects.
Note that the effect size (and thus the SSSRs) is rather small, resulting in a small AUR. Consequently, even small absolute differences between the estimated effects of interest and the SSSRs result in a relatively large pABCtime.
5.1.3. Prognostic Index
In addition to the two prognostic factors, we use the prognostic index 

5.2. Simulation Study
A more intuitive application of ABCtime is the comparison of different modelling alternatives in a simulation study. Because the true effect is known, application of ABCtime is straight-forward. The CoxPH, FPT and Timecox models are fitted to the data and are compared via pABCtime with logrank like weights in each of the 1000 simulated data sets. The significance level for testing on time-varying effects in FPT and Timecox is chosen to be 1%.
Figure 5 shows the effects for the non-linearly decreasing effect estimated by the three modelling approaches. From such a display, it can easily be seen that the CoxPH model performs worst, but judgement about the two time-varying approaches, again, is difficult. Both approaches differ in some general aspects. FPT fits a global
Figure 5. Simulation study, non-linearly decreasing effect. True effect (black solid) and effects estimated in 1000 replications (grey solid) by the Cox PH model (top left), FPT (top right) and Timecox (bottom left) and the corresponding distribution of pABCtime using logrank like weights (bottom right). Whiskers of boxplots extend to the 2.5% and 97.5% quantiles.
effect and thus results in very smooth, easy to interpret effect estimates, but at the expense of some deviating effects (e.g. artefacts). Timecox, on the contrary, uses a local fitting approach which results in very flexible but also potentially wiggly estimates. Thus, short-term changes in time-varying effects can be estimated very well, but with the potential disadvantage of blurring the global trend. However, these details on individual effects are difficult to see from graphical displays as individual curves are hidden by the mass but may cover a broad variety of different shapes (see Figure C6 and Figure C7 for examplary effects of different shape). pABCtime aggregates this information into one quantitative value, giving a measure of similarity to the true effect per simulated data set. The distribution of this measure over all 1000 simulation runs can easily be summarized, e.g. by boxplots (Figure 5, bottom right) and summary statistics, giving more detailed information about the variety of estimated effects. As expected from the graphical display of estimated effects, the CoxPH model performs considerably worse than FPT and Timecox, while the latter two approaches perform quite similar in terms of pABCtime. Yet, we also obtain the information that both approaches seem to be equally prone to artefacts in estimated effects. Additionally, we can see that Timecox has a slightly larger range of pABCtime over simulation runs with some larger deviations from the true effect (large pABCtime), but on the contrary was also closer to the true effect in several simulation runs.
In the setting with linearly decreasing effect, pABCtime reflects and refines the visual comparison of estimated effects equally well. Here, the shadow plots (Figure C8) indicate that the CoxPH model may not be considerably worse than the other two methods. FPT and Timecox, though, seem to fit nearly identical effects apart from some individual simulation runs.
6. Discussion
In applications with time-varying effects, a measure is required which quantifies, for example, the benefit of a time-varying effect compared to a standard CoxPH effect or a time-varying effect obtained from a different analysis method. If such a measure is available, and assuming that the smoothed scaled Schoenfeld residuals (SSSRs) reflect the true data well, they can be used to assess the fit of a function. Furthermore, in simulation studies the fit of two or more functions can be compared to the known true effect. With simulation studies in mind, we developed the ABCtime measure by adapting the measure of Govindarajulu et al. [10] to time-varying effects.
6.1. ABCtime as a Measure of Distance
In applications with known true effects, ABCtime is a straight-forward measure to quantify the distance between (time-varying) effects and the true effect. We conducted a simulation study to verify that ABCtime reflects the similarity to the true effect as it is supposed to do. When comparing time-varying and time-constant effects, ABCtime was able to detect effects that were closer to the true effect. Results are, of course, influenced by the choice of weights. Our slight preference for the logrank like weights resulted in a limited ability to detect time- varying behaviour in regions with less data support. In real data examples, though, we believe this is not a disadvantage, as deviations from PH in such regions are often a result of overfitting the data and/or of minor importance.
In the data example where the true effects are unknown, SSSRs were used as reference function to describe the underlying time-varying pattern of covariate effects. ABCtime enabled comparison between a constant CoxPH effect and two time-varying effects of different complexity. It clearly showed that the time-varying effects were considerably closer to the reference function than the CoxPH effect. This fact could also be revealed by graphical comparison of estimated effects. Differentiating between different time-varying effects such as the FPT and Timecox functions based on graphics, however, may be difficult, especially if their shapes are different, but none of them appears to be definitely closer to the reference. ABCtime yields a quantitative measure of the similarity which enables a comparison of different functions with the opportunity of up- or downweighting specific (time) regions of interest via the choice of weights. In our examples, ABCtime revealed that the time-varying approaches gave a better approximation to the SSSRs than the standard CoxPH model in all investigated settings, while the two of them were judged to perform similarly well, differing mainly in their variability. The variability of approaches is assessed by means of bootstrap percentile intervals of pABCtime, which also reflect the sensitivity of effect estimates obtained by the different approaches to slight changes in the data (e.g. their sensitivity to produce artefacts or “strange” shapes).
Thus, the ABCtime helps in specifying how well an estimated effect reflects the true or reference effect and gives an easily interpretable quantification of the “similarity” or distance between selected (time-varying) effects.
6.2. Choice of Reference Function
Although we restricted our investigation to the FPT and Timecox approaches, ABCtime is not limited to these methods, but is applicable to a broad variety of different approaches for modelling time-varying effects. One important aspect, however, is the specification of an appropriate reference function. The reference function has a very strong influence on the ABCtime measure and thus should be chosen with care. In simulation studies, the true effect itself naturally defines the reference. Despite of minor problems in more extreme situations (e.g. very large covariate effects or extreme covariate distributions with outlying values [17] ), SSSRs seem a reasonable choice to reflect the raw data in real life examples where the true effect is unknown. Yet, SSSRs raise the question of a suitable smoother and amount of roughness. The reference function shall reflect the true underly- ing behaviour of effects and thus should be flexible enough to reflect the underlying time-varying behaviour including possible short-term changes, but on the contrary should not be too wiggly.
6.3. Weighting Schemes
In this paper we investigated four different weighting schemes. In applications, the choice of weights should be motivated by the aim of the analysis and the choice of reference. In our examples, we have a slight preference for the logrank like weights, because they down weight differences at later times where few subjects are under risk. For tests of two survival functions, logrank like weights are the typical choice because they have good properties in the two sample case. These weights, as well as the inverse reference variance based weights, are straight-forward choices independent of the approaches to be compared. The inverse mean variance based weights, on the contrary, adjust for uncertain estimates in the approaches under investigation, but are simulta- neously subject to artefacts. Equal weights are the simplest choice, since they do not depend on the specific data and make interpretation easy. Yet, they do not adjust for regions with larger uncertainty or less data support.
Like many other flexible functions, the FP class is prone to produce artefacts at both ends. Therefore, we truncated the edges of the time scale from the calculation of ABCtime to reduce distortion of the measure by such artefacts and uncertain estimates. This is a kind of extreme downweighting of edges with weight = 0. Here, we define these edges as times beyond the 1% and 99% quantiles of event times.
6.4. Extreme Values and Robustness of Effects
Another possibility to avoid a distortion by artefacts is to reduce them already in the estimation process. Many approaches for time-varying effects, including the FPT algorithm, are sensitive to extreme survival times. If a data set contains many extremely small or large survival times, these time points may distort functional forms strongly, resulting in an inappropriate functional form or artefacts at the edges. This problem is already known from modelling FP functions of covariates. Royston and Sauerbrei [18] proposed a robustness transformation which reduces the leverage of extreme values and maps them smoothly to asymptotes, while the bulk of observed values is transformed almost linearly. This concept can easily be transferred to survival times (see Appendix, Section B, for more details).
6.5. Limitations and Extensions
The ABCtime measure is helpful in comparing time-varying effects. In some applications, though, especially when decisions about different methods for modelling time-varying effects are to be made, the resulting measure of distance may not give sufficient information to decide which approach is most suitable for the underlying problem. In these cases not only the raw distance of curves may be of interest, but also whether the shape of selected effects is correct. For example, if the true effect is strictly decreasing, the selected effect may only be acceptable if it is also decreasing and not, for instance, unimodal. On the contrary, if the true effect is unimodal, the position and/or size of the mode might be of great importance. In this case, an estimated non-unimodal effect would be unacceptable, though it might give a good ABCtime. Thus a qualitative measure as proposed by Bin- der, Sauerbrei and Royston [19] and adapted to time-varying effects by Buchholz [16] which specifies whether certain qualitative criteria defined by the true function are met (e.g. monotonicity, local extrema in a certain region or larger slope in a certain region) may be of additional help in decisions about appropriate methods for modelling time-varying effects.
Acknowledgements
We thank Maxime Look and John Foekens (Rotterdam breast cancer series) to make the data publicly available. We thank Clemens Wachter for his help in the preparation of the manuscript. Willi Sauerbrei and Anika Buchholz gratefully acknowledge the support from Deutsche Forschungsgemeinschaft (SA 580/8-1).
References
- Cox, D.R. (1972) Regression Models and Life-Tables. Journal of the Royal Statistical Society, Series B: Methodological, 34, 187-220.
- Schoenfeld, D. (1982) Partial Residuals for the Proportional Hazards Regression Model. Biometrika, 69, 239-241. http://dx.doi.org/10.1093/biomet/69.1.239
- Kneib, T. and Fahrmeir, L. (2007) A Mixed Model Approach for Geoadditive Hazard Regression. Scandinavian Journal of Statistics, 34, 207-228. http://dx.doi.org/10.1111/j.1467-9469.2006.00524.x
- Perperoglou, A., le Cessie, S. and van Houwelingen, H.C. (2006) Reduced-Rank Hazard Regression for Modelling Non-Proportional Hazards. Statistics in Medicine, 25, 2831-2845. http://dx.doi.org/10.1002/sim.2360
- Scheike, T.H. and Martinussen, T. (2004) On Estimation and Tests of Time-Varying Effects in the Proportional Hazards Model. Scandinavian Journal of Statistics, 31, 51-62. http://dx.doi.org/10.1111/j.1467-9469.2004.00372.x
- Berger, U., Schäfer, J. and Ulm, K. (2003) Dynamic Cox Modelling Based on Fractional Polynomials: Time-Variations in Gastric Cancer Prognosis. Statistics in Medicine, 22, 1163-1180. http://dx.doi.org/10.1002/sim.1411
- Sauerbrei, W., Royston, P. and Look, M. (2007) A New Proposal for Multivariable Modelling of Time-Varying Effects in Survival Data Based on Fractional Polynomial Time-Transformation. Biometrical Journal, 49, 453-473. http://dx.doi.org/10.1002/bimj.200610328
- Grambsch, P.M. and Therneau, T.M. (1994) Proportional Hazards Tests and Diagnostics Based on Weighted Residuals Biometrika, 81, 515-526. http://dx.doi.org/10.1093/biomet/81.3.515
- Sauerbrei, W., Royston, P. and Binder, H. (2007) Selection of Important Variables and Determination of Functional Form for Continuous Predictors in Multivariable Model Building. Statistics in Medicine, 26, 5512-5528. http://dx.doi.org/10.1002/sim.3148
- Govindarajulu, U.S., Spiegelman, D., Thurston, S.W., Ganguli, B. and Eisen, E.A. (2007) Comparing Smoothing Techniques in Cox Models for Exposure-Response Relationships. Statistics in Medicine, 26, 3735-3752. http://dx.doi.org/10.1002/sim.2848
- Royston, P. and Altman, D.G. (1994) Regression Using Fractional Polynomials of Continuous Covariates: Parsimonious Parametric Modelling. Applied Statistics, 43, 429-453. http://dx.doi.org/10.2307/2986270
- Efron, B. and Tibshirani, R. (1993) An Introduction to the Bootstrap. Chapman and Hall, New York. http://dx.doi.org/10.1007/978-1-4899-4541-9
- Buchholz, A. and Sauerbrei, W. (2011) Comparison of Procedures to Assess Non-Linear and Time-Varying Effects in Multivariable Models for Survival Data. Biometrical Journal, 53, 308-331. http://dx.doi.org/10.1002/bimj.201000159
- Altman, D.G., Lausen, B., Sauerbrei, W. and Schumacher, M. (1994) Danger of Using “Optimal” Cutpoints in the Evaluation of Prognostic Factors. Journal of the National Cancer Institute, 86, 829-835. http://dx.doi.org/10.1093/jnci/86.11.829
- Foekens, J.A., Peters, H.A., Look, M.P., Portengen, H., Schmitt, M., Kramer, M.D., Brünner, N., Jänicke, F., Meijer-van Gelder, M.E., Henzen-Logmans, S.C., van Putten, W.L.J. and Klijn, J.G.M. (2000) The Urokinase System of Plasminogen Activation and Prognosis in 2780 Breast Cancer Patients. Cancer Research, 60, 636-643.
- Buchholz, A. (2010) Assessment of Time-Varying Long-Term Effects of Therapies and Prognostic Factors. Ph.D. Thesis, Technische Universität Dortmund, Dortmund. http://hdl.handle.net/2003/27342
- Winnett, A. and Sasieni, P. (2001) Miscellanea. A Note on Scaled Schoenfeld Residuals for the Proportional Hazards Model. Biometrika, 88, 565-571. http://dx.doi.org/10.1093/biomet/88.2.565
- Royston, P. and Sauerbrei, W. (2007) Improving the Robustness of Fractional Polynomial Models by Preliminary Covariate Transformation: A Pragmatic Approach. Computational Statistics & Data Analysis, 51, 4240-4253. http://dx.doi.org/10.1016/j.csda.2006.05.006
- Binder, H., Sauerbrei, W. and Royston, P. (2011) Multivariable Model-Building with Continuous Covariates: 1. Performance Measures and Simulation Design. Technical Report 105, University of Freiburg, Freiburg.
Appendix
A. Influence of Artefacts on the Inverse Mean Variance Weights
Figure A1(a) shows the variances of FPT, Timecox and CoxPH effects for 


Figure A1. Rotterdam,

B. Extreme Times and Artefacts
Many approaches for time-varying effects are sensitive against extreme survival times. If a data set contains many extremely small or large survival times, these time points may distort functional forms strongly, resulting in an inappropriate functional form or artefacts at the edges.
Royston and Sauerbrei [18] proposed a robustness transformation which reduces the leverage of extreme values and maps them smoothly to asymptotes, while the bulk of observed values is transformed almost linearly. The approach has been developed within the framework of modelling FP functions of covariates, but the concept can easily be transfered to transformations of survival times (i.e. in modelling time-varying effects). The robustness transformation maps the survival times to 
where
with




C. Supplementary Figures and Tables
Figure C1. Rotterdam data. Smoothed scaled Schoenfeld residuals with 95% pointwise confidence intervals for the individual components of the multivariable model M1 of [7] and its prognostic index. Horizontal dotted lines show the parameter estimates from the PH model.
Figure C2. Rotterdam, hormon. Effects estimated by the FPT algorithm, the Timecox procedure, a CoxPH model and the reference function, the smoothed scaled Schoenfeld residuals. The vertical dashed lines mark the 1% and 99% quantiles of uncensored event times which define the time interval ABCtime is calculated on.
Figure C3. Rotterdam, hormon. Area between the curves (pABCtime in %) for the CoxPH model (left), the FPT algorithm (center) and the Timecox procedure (right) relative to the reference function (smoothed scaled Schoenfeld residuals) using different weights. Given are boxplots of pABCtime over 1000 bootstrap samples, where the mean pABCtime over bootstrap samples is marked by “×” and the whiskers of boxplots extend to the 2.5% and 97.5% quantiles, thus representing the 95% bootstrap percentile intervals. The pABCtime value calculated for the original data is marked by “♦”.
Figure C4. Rotterdam, hormon. Effects estimated in all bootstrap samples (grey) with some examplary bootstrap replications in which time-varying effects have been chosen that result in a large pABCtime (black).
Figure C5. Rotterdam, PI. Effects estimated by the FPT algorithm, the Timecox procedure and a CoxPH model and the reference function, the smoothed scaled Schoenfeld residuals. The vertical dashed lines mark the 1% and 99% quantiles of uncensored event times which define the time interval ABCtime is calculated on.
Figure C6. Simulation study, non-linearly decreasing effect. True effect function (solid) and 4 examplary effects estimated by FPT in the simulation runs (dashed).
Figure C7. Simulation study, non-linearly decreasing effect. True effect function (solid) and 4 examplary effects estimated by Timecox in the simulation runs (dashed).
Figure C8. Simulation study, linearly decreasing effect. True effect (black solid) and effects estimated in 1000 replications (grey solid) by the Cox PH model (top left), FPT (top right) and Timecox (bottom left) and the corresponding distribution of pABCtime using logrank like weights (bottom right). Whiskers of boxplots extend to the 2.5% and 97.5% quantiles.
Table C1. Rotterdam data. Grambsch-Therneau test for different choices of 
Table C2. Rotterdam data. Area between the curves fitted by the FPT algorithm, the Timecox procedure and the CoxPH model relative to the reference function (smoothed scaled Schoenfeld residuals) for different prognostic factors.































