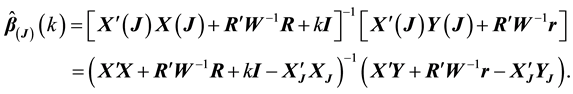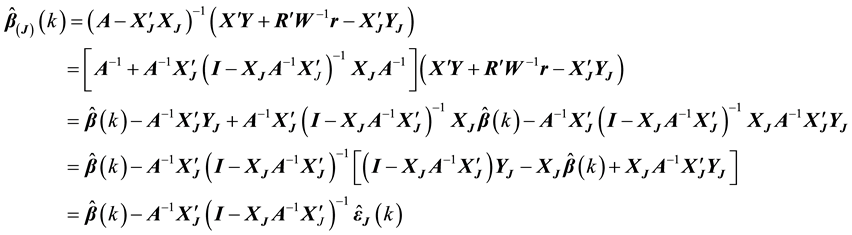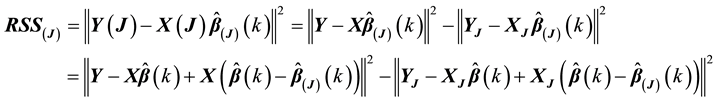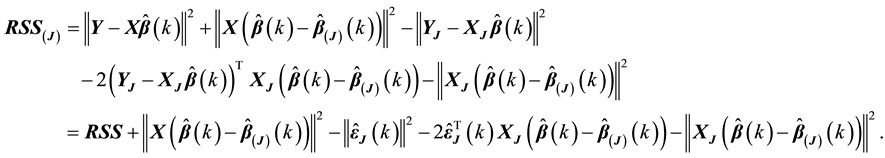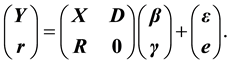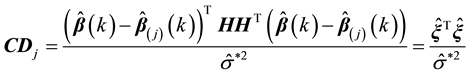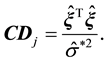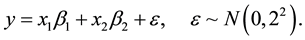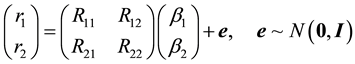Received 18 August 2014; revised 23 September 2014; accepted 2 October 2014

ABSTRACT

The aim of this paper is to propose some diagnostic methods in stochastic restricted linear regression models. A review of stochastic restricted linear regression models is given. For the model, this paper studies the method and application of the diagnostic mostly. Firstly, review the estimators of this model. Secondly, show that the case deletion model is equivalent to the mean shift outlier model for diagnostic purpose. Then, some diagnostic statistics are given. At last, example is given to illustrate our results.

Keywords:

Stochastic Restricted Linear Regression Model, Stochastic Restricted Ridge Estimator, Statistical Diagnostics

1. Introduction

In a linear regression, the ordinary least squares estimator (LS) is unbiased and has minimum variance among all linear unbiased estimators and has been treated as the best estimator for a long time. When the addition of stochastic linear restrictions on the unknown parameter vector was assumed to be held, Theil [1] proposed the ordinary mixed estimator (OME). Hubert and Wijekoon [2] proposed the stochastic restricted Liu estimator (SRLE). And Li and Yang [3] introduced the stochastic restricted ridge estimator (SRRE) by grating the ORE into the mixed estimation procedure. Wu [4] discussed stochastic restricted 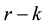class estimator and stochastic restricted 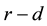class estimator in linear regression model. When the prior information and the sample information were not equally important, Schafrin and Toutenburg [5] introduced the method of weighted mixed regression and developed the weighted mixed estimator (WME). Li and Yang [6] grated the ORE into the weighted mixed estimation procedure and proposed the weighted mixed ridge estimator. Liu, et al. [7] proposed the stochastic weighted mixed almost unbiased ridge estimator by combining the WME and the AURE and also proposed the stochastic weighted mixed almost unbiased Liu estimator by combining the WME and the AULE in a linear regression model. He and Wu [8] proposed a new estimator to combat the multicollinearity in the linear model when there were stochastic linear restrictions on the regression coefficients. The new estimator is constructed by combining the ordinary mixed estimator (OME) and the principal components regression (PCR) estimator, which is called the stochastic restricted principal components (SRPC) regression estimator. Liu, Yang and Wu [9] introduced the weighted mixed almost unbiased ridge estimator (WMAURE) based on the weighted mixed estimator (WME) and the almost unbiased ridge estimator (AURE) in linear regression model. They discussed superiorities of the new estimator under the quadratic bias (QB) and the mean square error matrix (MSEM) criteria. Wu and Liu [10] considered several estimators for estimating the stochastic restricted ridge regression estimators. A simulation study has been conducted to compare the performance of the estimators. The result from the simulation study shows that stochastic restricted ridge regression estimators outperform mixed estimator.

Nearly forty years, the diagnosis and influence analysis of linear regression model has been fully developed (R.D. Cook and S. Weisberg [11] , Wei, et al. [12] ). Jiawei Wang [13] discussed the linear regression model with the random constraints, introduced its residuals and showed that the CDM was equivalent to the mean shift outlier model for diagnostics purpose based on general least square estimate. Lian Yang and Hu Yang [14] dealt with the data deleted model and the mean shift model under ellipsoidal restriction and obtained the equivalence of the diagonal statistic between the two models. Lu Wang [15] discussed the statistical diagnostic of multivariate linear regression model with linear restriction.

However, statistical diagnostics of stochastic restricted linear regression models based on stochastic restricted ridge estimator (SRRE) are studied in this paper. The paper is organized as follows. The model and the estimators are reviewed in Section 2. We show that the case deletion model is equivalent to the mean shift outlier model for diagnostic purpose in Section 3. Some diagnostic statistics are given in Section 4. The example to illustrate our results is given in Section 5.

2. Review of Stochastic Restricted Linear Regression Model

Consider the following linear model:

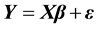, (1)

where 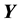is an 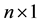vector of observatio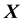n, is an 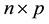design matrix of rank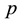, 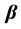is a vector denoting unknown coefficients, and 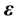is an 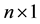random error vector with 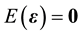and.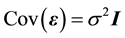

Suppose that 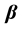satisfies the following stochastic restriction, that is,

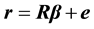, (2)

where is a nonzero matrix with and is a known vector, and. In this paper, we assumed that is independent of. And now model (1) is called stochastic restricted linear regression model.

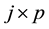
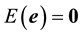
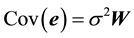
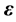
2.1. Estimates of Model

Using the mixed approach, Durbin [16] , Theil and Goldberger [17] introduced the mixed estimator (ME), which is defined as follows:

. (3)

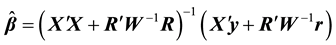
The mixed estimator is an unbiased estimator. However, when multicollinearity exists, the mixed estimator is no longer a good estimator.

Ozkale [18] proposed the following stochastic restricted ridge estimator (SRRE):

. (4)

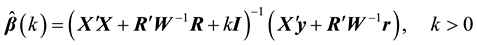
The result from the simulation study shows that SRRE outperform ME (see Wu and Liu [19] ).

2.2. Estimating k

The most classical ridge estimator for linear regression is the following:

,

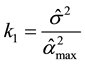
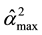
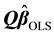
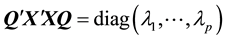
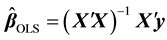
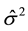
proposed by Hoerl and Kennard [20] , where denote the maximum element of,

, , and is the estimator of. Hoerl, et al. [21] introduced

an alternative of the estimator of, which is defined as follows:

.

In Schaefer, et al. [22] , a modified version of this estimator is proposed as follows:

.

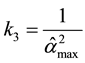
In Kibria, et al. [23] , a new estimator is proposed as follows:

.

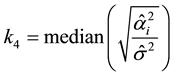
This paper selects 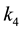to estimate below.

3. Diagnostic Methods

3.1. Case-Deletion Model

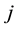
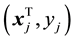
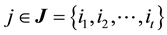
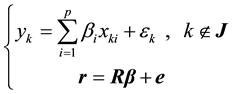
Consider the stochastic restricted linear model, where the -th case is deleted,.

(5)

This model is called case-deletion model. Supposed that the SRRE of the coefficient function in model (5) is.

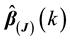
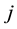
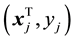
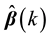
In order to study the influence of the -th case, and compare the difference between and. The important result as following theorem.

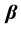
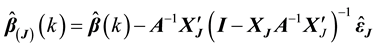
Theorem 1. For model (5), the SRRE of is

(6)

and

(7)

where,.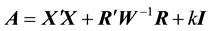

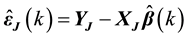
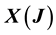
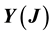
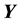
Proof: Let and corresponding to and to delete the cases which belong to. For model (5), we use the SRRE obtained that

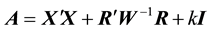
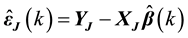
Supposed that, , then

which leads to (6).

Because

and,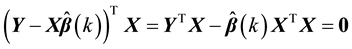

hence

3.2. Mean Shift Outlier Model

The other common statistical diagnosis model is the mean shift outlier model (MSOM). For the stochastic restricted linear regression model, the corresponding MSOM is

(8)

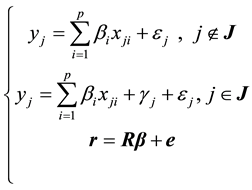
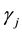
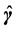
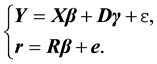
where the parameter are number, which describe the outlier. Let the SRRE of model (8) are and. The corresponding matrix formula of model (8) as follows:

(9)

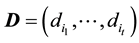
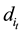
where, is a n-dimensional vector, the -th component is 1, and the other are zero.

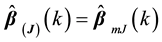
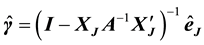
Theorem 2. For model (8), there are, and.

Proof: By the matrix form of model (8), we obtained

On the other hand, by the formula of calculating the inverse matrix of partitioned matrix, we have

which leads to and.

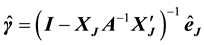
4. Diagnostical Statistics

4.1. Generalized Cook Distance

Let is a nonnegetive matrix and is one real number. The generalized Cook distance of the -th case is defined as follows:

(10)

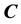
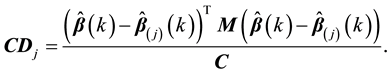
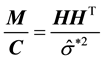
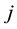
Theorem 3. Supposed that, then the generalized Cook distance of the -th case is

where,.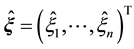

Proof: Because

Substituting these results into (9) gives

4.2. W-K Statistic

W-K statistic is advanced from the view of data fitting. Considering the influence of the -th case. In order to eliminate the influence of scale, it is also need to divide the variance of estimator. Because the keystone is to review the influence of deleting the -th case. Hence, is substituted by. Then, the W-K statistic can be expressed as follows:

(11)

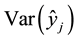
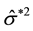
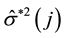
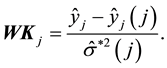
4.3. Covariance Ratio Statistic

is to measure the superiorities of. The covariance ratio statistic is defined as follows:

,

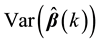
which measure the influence of the -th case.

5. Monte Carlo Experiments

In order to illustrate the validity of above results, extensive Monte Carlo sampling experiments were conducted. To evaluate the finite-sample performance of our proposed method, we simulate 60 random samples from the following model:

The stochastic restricts as follows:

where,. In order to checkout the validity of our proposed metho-

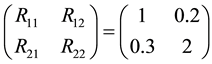
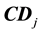
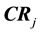
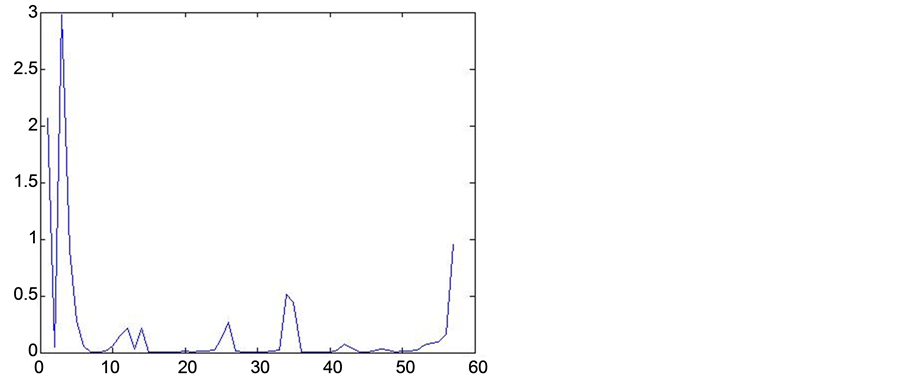
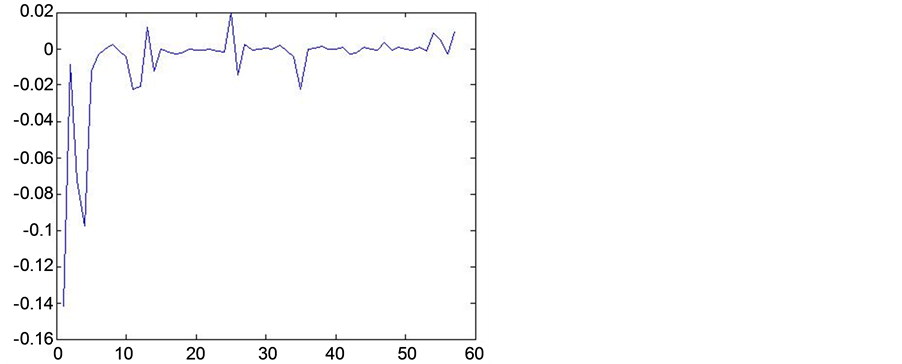
dology, we change the value of the first, 125th and 374th data. For every case, it is easy to obtain, and.

From the Figure 1, Figure 2, Figure 3, we can see that in most cases, the value of are reasonably close to one fixed value. Following the definition and properties of diagnosis statistics, we can diagnose the strong influence points, the value of which deviate from the average seriously. Figure 2 and Figure 3 show that the first and the third data are strong influence points. Indeed, our results are illustrated.

6. Conclusion

In this paper, stochastic restricted linear regression models are revisited. Useful diagnostic methods are derived. Through simulation study, we illustrate that our proposed methods can work fairly well.

References