Int'l J. of Communications, Network and System Sciences
Vol. 5 No. 1 (2012) , Article ID: 17145 , 6 pages DOI:10.4236/ijcns.2012.51001
Computation of Complex Primes Using Elliptic Curves: Application for Cryptosystem Design
Computer Science Department, New Jersey Institute of Technology, Newark, USA
Email: verb73@gmail.com
Submitted December 01, 2011; accepted January 16, 2012
Keywords: Communication Security; Gauss Formula; Complex Primes; Points Counting; Modular Elliptic Curve; Applets; Dual Elliptic Curves
ABSTRACT
This paper provides several generalizations of Gauss theorem that counts points on special elliptic curves. It is demonstrated how to implement these generalizations for computation of complex primes, which are applicable in several protocols providing security in communication networks. Numerical examples illustrate the ideas discussed in this paper.
1. Introduction and Gauss Formula for Counting Points
Knowledge of how to count the number of points on elliptic curve (EC) provides certain advantage in the design of cryptographic systems for secure communication in various applicational environments (transfer of funds in banking, transmission of sensitive information between inventor and his/her attorney, national security agencies, military applications, diplomatic communications, governmental operations, control of weapons of mass distraction, telemedicine etc.). In general, algorithms for counting points on an EC are in the domain of algebraic [1,2] and algorithmic number theories [3,4]. Only in special cases it is possible to provide a closed-form solution [5]. Although validation of these algorithms requires application of algebraic number theory, which is beyond the scope of this paper, their description is rather easy to understand for cryptographers and application-oriented computer scientists.
In this paper we provide several generalizations of Gauss theorem and then demonstrate how to apply them in selection of complex prime parameters for the design of the cryptographic systems. These generalizations are based on intensive computer experiments (CE). As a result, not all proofs that validate the algorithms are provided. Instead, we formulate various conjectures and propositions that are supported by results of these CE.
1.1. Gauss theorem: Consider the elliptic curve (EC)
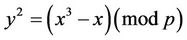 , (1.1)
, (1.1)
where p is a real prime; let E denote the number of ordered integer pairs (x, y) that satisfy Equation (1.1); every such integer pair (x, y) is called a point on the EC. There are two major cases:
1). If pmod4=3, then EC (1.1) has p points {excluding the point at infinity O [1]};
2). If pmod4=1; , where C is odd; (1.2)
, where C is odd; (1.2)
and
(C+F)mod4=1;(1.3)
then
 (1.4)
(1.4)
{excluding the point at infinity O} [4].
If Condition (1.3) holds, then the Gauss Formula (1.4) can be applied to compute a complex prime (C, F). This application is based on the observation that an ordered pair of integers (C, F):=C+iF is a complex prime if and only if its norm  is a prime [5].
is a prime [5].
However, not all complex primes have components C and F that satisfy (1.3). For instance, (C, F)=(5,2) is the complex prime; yet (5+2)mod4=3.
Therefore, the algorithm provided below is non-deterministic, since its application is restricted by C. F. Gauss Theorem [5].
1.2. Non-deterministic algorithm for computation of complex primes:
Step1: Select a prime pmod4=1;
Step2: Count the number of points E on EC
 (1.1);
(1.1);
Step3: Compute
 ;
;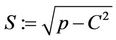 (1.5)
(1.5)
Step4: If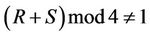 , then repeat Steps 1-4;
, then repeat Steps 1-4;
Step5: If R is odd, then (C, F):=(R, S)
else (C, F):=(S, R).(1.6)
Remark1.1: Although this algorithm is not deterministic, yet, after s trials it finds a complex prime (C, F) with probability .
.
Integers 61, 977, 1777, 1913, 1933, 4133 are examples of primes, for which Condition (1.3) does not hold.
The following conjectures and propositions generalize Gauss theorem and, as a byproduct, allow to design a deterministic algorithm that computes complex primes for every real non-Blum prime p {pmod4=1}. These propositions and conjectures also provide insights that help to understand how various criteria were derived and applied for integer factorization algorithms that were described in papers [6,7] recently-published by the author of this paper.
2. Generalizations of Gauss Theorem
As it is shown below, in certain cases the number of points 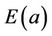 on EC
on EC
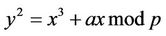 (2.1)
(2.1)
can be represented as
 (2.2)
(2.2)
where G(a, C, F) is equal either 1 or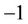 .
.
Remark2.1: In all following discussions, the point at infinity 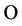 is excluded from the counting.
is excluded from the counting.
Conjecture2.1: Consider the elliptic curve (1.1), where p is a prime; if Condition (1.2) holds, then
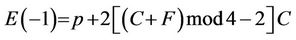 (2.3)
(2.3)
Conjecture2.2: Consider elliptic curve (EC)
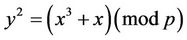 (2.4)
(2.4)
where p is a prime and let condition (1.2) holds; then for every F
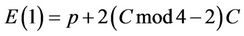 (2.5)
(2.5)
Conjecture2.3: Consider EC
 (2.6)
(2.6)
where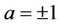 ; and let (1.2) holds; then
; and let (1.2) holds; then
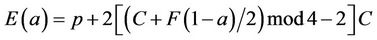 (2.7)
(2.7)
Corollary: Equation (2.7) implies that if Fmod4=0, then elliptic curves (1.1) and (2.4) have equal number of points {see Table 2.1}.
Equation (2.7) can be also presented as
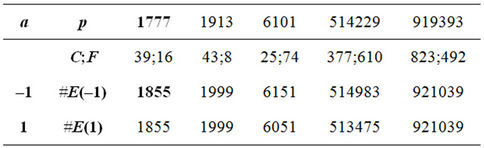
Table 2.1. Generalized Gauss formula if EC is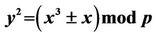 .
.
 (2.8)
(2.8)
The table above provides examples of randomlyselected non-Blum primes that confirm formulas (2.3), (2.5) and (2.7).
Remark2.2: Elliptic curve (1.1) considered by C.F. Gauss has a remarkable property: if p=1777, then E(–1)=1855 {C.F. Gauss was born in 1777 and died in 1855}, (see Table 2.1). The same property holds for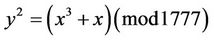 : E(1)=1855.
: E(1)=1855.
3. Points on Elliptic Curves
In some applications and applets it is necessary to find at least one solution of modular Diophantine equations
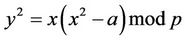 (1.1);
(1.1);
or
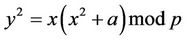 (2.4).
(2.4).
Several special cases are listed below, where such solutions can be provided in closed forms.
Case1: If
 (3.1)
(3.1)
then for every 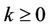
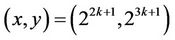 (3.2)
(3.2)
is on EC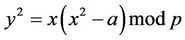 .
.
Case2: If
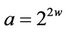 (3.3)
(3.3)
then for every odd w
 (3.4)
(3.4)
is the point on EC
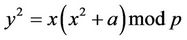 (3.5)
(3.5)
Case3: Let ;
;
consider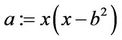 (3.6)
(3.6)
then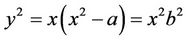 .
.
Therefore, y = bx, i.e., (x, bx) is on EC
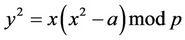 (3.7)
(3.7)
Hence, if a=5, or a=6, or a=–3, then respectively (5,10), (3,3), (3,6) are the points on (3.7).
4. Counting Points on Elliptic Curves with 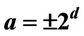
In order to design an efficient algorithm that computes complex primes, it is necessary to know how to count points on EC (2.1), where |a| is not equal 1; {see Section 8 for an explanation}.
Consider an EC
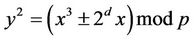 (4.1)
(4.1)
where exponent d is a non-negative integer; p is a prime, pmod4 = 1;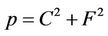 ; let
; let  denote the number of points on the EC (4.1).
denote the number of points on the EC (4.1).
Elliptic curves with coefficients 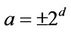 have remarkable cyclic properties.
have remarkable cyclic properties.
Proposition4.1: If Fmod8=0;(4.2)
then 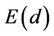 is independent of exponent d, i.e., is the same for all d; and
is independent of exponent d, i.e., is the same for all d; and
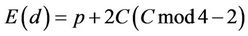 (4.3)
(4.3)
Proposition4.2: If Fmod8=4;(4.4)
then
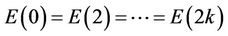 ;
;
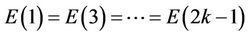 (4.5)
(4.5)
and
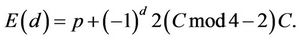 (4.6)
(4.6)
Proposition4.3: If Fmod4=2, then the number of points on the EC is equal
 (4.7)
(4.7)
Proposition4.4: For every non-negative integer d the following equation holds
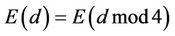 (4.8)
(4.8)
Proposition4.5: If Fmod4=2, and if d=2m<4, then for m=0 and m=1 the following equations hold:
 (4.9)
(4.9)
if d=2m+1<4, then
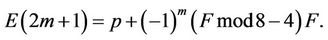 (4.10)
(4.10)
Table 4.1 illustrates all cases considered in Propositions 4.1-4.5.
5. Counting Points on Dual EC
Proposition5.1: Let 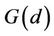 be the number of points on the dual EC
be the number of points on the dual EC
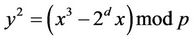 (5.1)
(5.1)
then for every non-negative integer d
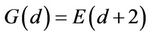 (5.2)
(5.2)
Proof is provided in [7].
Tables 4.1 and 5.1 illustrate Proposition 5.1.
6. Counting Points: Detailed Description
In this section we provide a detailed description on how to count the points on the EC (5.1).
Conjecture6.1: If prime pmod4=1; , where C is odd; and Fmod4=2, then the number of points
, where C is odd; and Fmod4=2, then the number of points 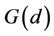 on EC
on EC 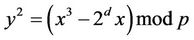 is equal
is equal
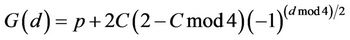 (6.1)
(6.1)
if d is even;
however, if d is odd, then there are two cases:
 (6.2)
(6.2)
a). if d=4k+1; then G(d)=p+F(4–Fmod8);(6.3)
b). if d=4k+3, then G(d)=p–F(4–Fmod8). (6.4)
The following formula summarizes all cases of Conjecture 6.1 for odd d:
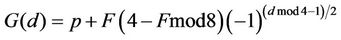 (6.5)
(6.5)
Conjecture6.2: If Fmod8=4,(6.6)
then for every integer k
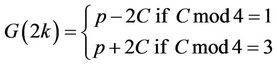 (6.7)
(6.7)
and
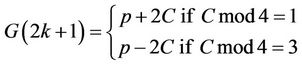 (6.8)
(6.8)
Conjecture6.3: If Fmod8=0,(6.9)
then for every d
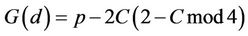 (6.10)
(6.10)
Proposition6.4: For every integer b, d and non-Blum prime p elliptic curves
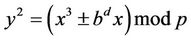 ;
;
and
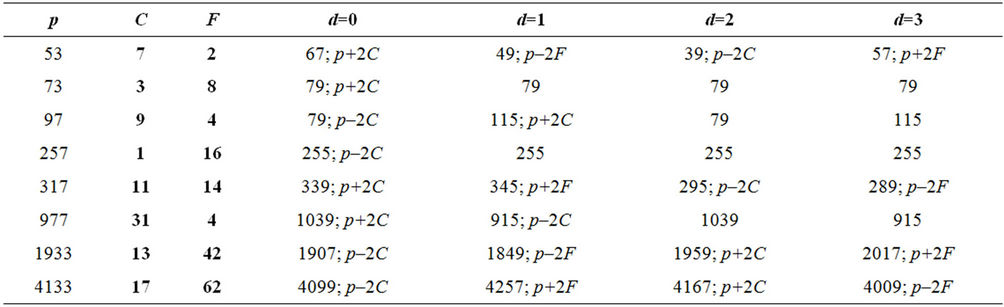
Table 4.1. Number of points on EC y2=(x3+2dx)modp.

Table 5.1. Number of points on EC y2=(x3–2dx)modp.
 (6.11)
(6.11)
have the same number of points. Proof is provided in [7].
7. Computation of Complex Primes: Deterministic Algorithm
Since the complex integer (C, F) is a prime if and only if its norm
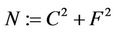 (7.1)
(7.1)
is a prime, in a naïve approach we can first select a nonBlum prime p, and then find its representation as a sum of two integer squares (7.1). The complexity of such an algorithm is of order 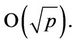 Instead we can apply the generalization of Gauss Theorem described above; {for further details see Table A1 in the Appendix}.
Instead we can apply the generalization of Gauss Theorem described above; {for further details see Table A1 in the Appendix}.
Step1: Select a prime pmod4=1;
Step2: Count the number of points E(a) on EC
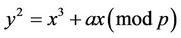 , where
, where
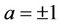 (7.2)
(7.2)
Step3: Compute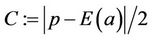 ; and
; and
 (7.3)
(7.3)
Example7.1: Let p=433494437;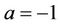 ; then E(–1)=433459015; and (C, F)=(17711,10946).
; then E(–1)=433459015; and (C, F)=(17711,10946).
8. Complexity Analysis
Schoof-Elkies-Atkin (SEA) algorithm counts points on elliptic curves 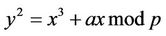 with expected running time
with expected running time 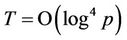 if
if 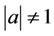 [1]; {the SEA is not applicable if
[1]; {the SEA is not applicable if  =1}. Therefore, if
=1}. Therefore, if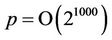 then
then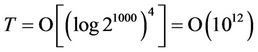 .
.
9. Conclusions and Unsolved Problem
In this paper we considered families of modular equations (called the EC) and corresponding algorithms that counts the number of integer points on each of these ECs. For all these cases we provided closed-form solutions with one exception {see Section A3 in Appendix, where we provided that case as a Challenge to the readers of this paper}.
Finally, we provided a deterministic algorithm with polynomial time complexity that computes a complex prime (C, F) for every real prime p. In [9] is demonstrated how to implement the complex primes in cryptographic systems based on double moduli reduction, where one modulus is a real prime and another modulus is a complex prime.
10. Acknowledgements
I express my gratitude to K. Engemann, D. Kanevsky and R. Rubino for their comments and to my former students for their assistance in creation of applets that count the number of points on elliptic curves based on my algorithms. Results of computer experiments provided in this paper were performed using these applets.
REFERENCES
- R. Lercier, D. Lubicz and F. Vercauteren, “Point counting on elliptic and hyperelliptic Curves,” In: H. Cohen and G. Frey, Eds., Handbook of Elliptic and Hyperelliptic Curve Cryptography, Chapman and Hall/CRC, Boca Raton, 2006, pp. 407-453.
- K. Rubin and A. Silverberg, “Ranks of Elliptic Curves,” Bulletin American Mathematical Society (New Series), Vol. 39, No. 4, 2002, pp. 455-474. doi:10.1090/S0273-0979-02-00952-7
- A. Lauder and D. Wan, “Counting points on variety over finite fields of small characteristics,” In: J. P. Buhler and P. Stevenhagen, Eds., Algorithmic Number Theory, Cambridge University Press, New York, 2008, pp. 579- 612.
- R. Schoof, “Counting points on elliptic curves over finite fields”, Journal de Theorie des Nombres de Bordeaux, Vol. 7, No. 1, 1995, pp. 219-254. doi:10.5802/jtnb.142
- C. F. Gauss, “Disquisitiones Arithmeticae,” Verlag, Gottingen, 1863, p. 483.
- B. Verkhovsky, “Integer factorization of semi-primes based on analysis of a sequence of modular elliptic equations,” International Journal of Communications, Network and System Sciences, Vol. 4, No. 10, 2011, pp. 609- 615. doi:10.4236/ijcns.2011.410073
- B. Verkhovsky, “Algorithms for integer factorization based on counting solutions of various modular equations,” International Journal of Communications, Network and System Sciences, Vol. 4, No. 11, 2011, pp. 675-682. doi:10.4236/ijcns.2011.411083
- L. Dewaghe, “Remarks on the Schoof-Elkies-Atkin Algorithm,” Mathematics of Computation, Vol. 67, No. 223, 1998, pp. 1247-1252. doi:10.1090/S0025-5718-98-00962-4
- B. Verkhovsky, “Double-moduli Gaussian encryption/decryption with primary residues and secret controls,” International Journal of Communications, Network and System Sciences, Vol. 4, No. 8, 2011, pp. 475-481. doi:10.4236/ijcns.2011.47058
APPENDIX
A1. Computer experiments

Table A1. Generation of Gaussian primes via EC y2=x3+ax(modp).

Table A2. Generation of Gaussian primes using EC y2=x3–2x(modp).
A2. Generalizations
Consider
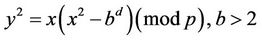 ; (A1)
; (A1)
CaseA1: If 2 is a generator or there exists an integer z such that
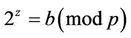 ; (A2)
; (A2)
then consider
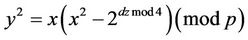
and find E(dzmod4), {see (5.1) and (5.2)}.
ExampleA1: Let p=73, b=37, d=2; then 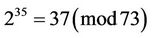 , i.e. z=35.
, i.e. z=35.
ThereforeE(dzmod4)=E(70mod4)=E(2); (6.5).
Since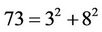 , then E(2)=79.
, then E(2)=79.
CaseA2: If b is a generator or there exists an integer w such that
 , (A3)
, (A3)
then
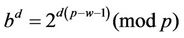 .
.
Now consider
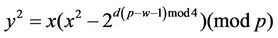 ; (A4)
; (A4)
and find E(d(p–w–1)mod4).
CaseA3: Conjectures A1-A3 address the cases where an

Table A3.1. # of points E(3,0) on y2=(x3–3dx)modp; if d=1, then E(3,1)=p+2F.

Table A3.2. # of points E(3,0) on y2=(x3–3dx)modp; if d=1, then E(3,1)=p–2F.
integer solution z of Equation (A2) does not exist.
ConjectureA1: If gcd(CF, b)=1, then there are four distinct counts for d=0,1,2,3:
E(3,0)=p+(Cmod4–2)(1–Fmod4); (A5)
E(3,2)=2p–E(3,0); (A6)
and E(3,3)=2p–E(3,1);(A7)
{see Tables A3.1 and A3.2}.
ConjectureA2: If gcd(CF,b)>1, then there are two distinct counts: 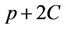 and
and ; {see Table A4}; namely:
; {see Table A4}; namely:
a). ; (A8)
; (A8)
b). if gcd(CF, b) = 1then
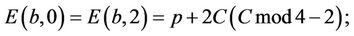 (A9)
(A9)
c). if Fmodb=0 or {b|C and Fmod4=0}, then
 (A10)
(A10)
ConjectureA3: If b|C and Fmod4=2, then for every d
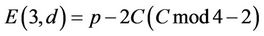 ; (A11)
; (A11)
if Fmod4b=0, then for every d
 . (A12)
. (A12)
Table A5 illustrates all cases of ConjectureA3.
A3. Unsolved Problem
We leave to the readers to figure out a formula for E(3,1) provided that (A7) holds and E(3,1) is equal either  or
or , {see above Tables A3.1 and A3.2}.
, {see above Tables A3.1 and A3.2}.

Table A4. E(3,0)=E(3,2); E(3,1)=E(3,3).

Table A5. E(3,0)=E(3,1)=E(3,2)=E(3,3).

