Journal of Water Resource and Protection
Vol.09 No.09(2017), Article ID:78120,19 pages
10.4236/jwarp.2017.99070
Evaluation of Fast Flood Diffusion through a Drainage Channel: A Flood Disaster Case Study of Japan’s Kinugawa River, September 10, 2015
Kazuaki Ohtsuki, Yasuo Nihei
Department of Civil Engineering, Tokyo University of Science, Chiba, Japan

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: June 2, 2017; Accepted: July 30, 2017; Published: August 2, 2017
ABSTRACT
On September 10, 2015, unprecedented flood was occurred in Kinugawa River basin located on eastern Japan. It inundated 40 km2 of flood plain in Joso city, Ibaraki Prefecture, and more than 4000 people there called for help despite supposedly having sufficient time to evacuate. Some said that small initial flood before main severe flood arrived made them make a mistake in deciding whether to evacuate or stay there, despite having to actually evacuate in reality. This study focused on flood behaviour in this area, in particular, the effect of a small drainage channel lying on the flood plain which caused fast flood diffusion in case of occurring huge overflowing. Field investigations starting on time of the disaster with high-resolution positioning system were conducted to obtain spatial maps of flood depth and height. For appropriate modelling of the effect of small channel, we applied simulation model coupling 1-dimensional (1D) and 2-dimensional (2D) hydraulic scheme on the field and compared results from the 1D/2D coupled model and model without 1D scheme. The models provided information that the flood could reach 4 hours earlier to the city central of Joso city comparing in case of model without 1D scheme. The water depth rose irregularly and it was more confusing and difficult for the victims to make appropriate evacuation act.
Keywords:
Flood Diffusion, 1- and 2-Dimensional Coupled Flood Simulation, Channel, Kinugawa River

1. Introduction
Japan is located in a monsoon zone and, thus, is one of the rainiest countries in the world. Most of Japan’s cities lie on alluvial plains in which the flood risk is relatively high, so historically we have suffered a large number of floods. Many flood protection measures have been implemented, including structural countermeasures, alert systems and evacuation planning and procedures. However, recently, we experienced incredibly strong rainfalls, perhaps as a result of global climate change, resulting in extremely severe disasters in Yamaguchi in 2013, Hiroshima and Izu-Oshima in 2014, to name a few. In Yamaguchi, a continual downpour of two hours that exceeded 130 mm/hour inundated the town of Susa very quickly and completely. Hiroshima experienced more than 100 mm/hour of severe rainfall, and a number of debris flows struck hillside residences, resulting in eight victims losing their lives. And it is feared that extremely heavy rainfalls such as these will increase in the future. These unprecedented rainfalls brought flood patterns we had never before experienced. Therefore, it is important to learn as much as possible about them to determine whether existing flood protection facilities, warning systems and evacuation schemes remain effective.
On September 9, 2015, an especially severe rainfall was brought on by two strong typhoons, Nos. 17 (Kilo) and 18 (Etan), in Kanto and the South Tohoku region, in eastern Japan. Serious flooding occurred in the Kinugawa River basin, located in the prefectures of Tochigi and Ibaraki in the Kanto region (Figure 1(a) and Figure 1(b)). Due to the severe flood, a levee failure and flood overtopping happened, and they inundated around 40 km2 area of the flood plain in the city of Joso, Ibaraki Prefecture (Figure 1(c) and Figure 2(a) and Figure 2(b)). In this disaster, one of the most remarkable facts is that more than 4000 inhabitants in the city needed to be rescued from their homes even though they might have had enough time to evacuate without assistance, because Joso’s city center is 10 km away from the riverbank failure point. In fact, there was little flooding in the city center before arrival of the main flood. Some residents said that this minimal initial flooding made them think the flood was smaller than they anticipated, and they decided to stay home, not realizing that they were actually facing unprecedented severe flood. In the flood plain, a drainage waterway called Hachikenbori-gawa Channel lies as shown in Figure 1(c) and Figure 2(c). It can be assumed that the flood water bumped into the channel and diffused downstream very quickly considering its high water depth. This accelerated diffusion of the flood through the channels or pipes has been discussed in inland flooding, especially in urban areas [1] [2] [3] . Though huge volume flows such as those caused by riverbank failures have not been a focus of much discussion, the effect of this fast diffusion can be significant.
To evaluate the interaction between channel facilities and floodplain properly, a 1D/2D coupled hydraulic model is effective [4] [5] . In particular, that kind of hydrodynamic model was applied to urban area using several commercial software applications for integrated flood simulation [4] [6] . In general, modeling of flood diffusion on flood plain is developed on the 2D field. Although computation performance has improved day by day, calculation grid size was set several meters long in practice, which is not enough to resolve geometry (width and volume) of small channel like we discussed. Including point of view of simulation
Figure 1. Example of a figure caption (figure caption). (a) and (b) study site of Kinugawa River basin, (c) map of the flood’s extent on 9/10/2015 in Kinugawa.
efficiency, 1D and 2D integrated flood model is needed for appropriate modeling for the situation.
According to this background, we studied the process of the flood diffusion, especially in focusing on acceleration by small channel, based on the case study of the unprecedented flood occurred in Kinugawa River basin, 2015. Essential information of the flood, site location, rainfall and flood intensity and official waring and evacuation, were provided for the first introduction. Flooding process was investigated from beginning of the flood, and inundation depth and absolute water level were also surveyed with high accurate positioning equipment. A simulation model capable 1D/2D model integration was applied to the field for appropriate modeling of small channels lying on broad flood plain. From the results after the model validation, we discussed the properties of the flood, shorter arriving time of flood, irregularity of flood depth rise and water balance, and future direction to the flood protection we should do.
2. Summary of the Flood Disaster
2.1. Site Location
The Kinugawa River basin is located in eastern Japan’s Kanto region (Figure 1(a) and Figure 1(b)). The Kinugawa is one of the largest branches of the Tonegawa River, which has the widest watershed in Japan. The Kinugawa River is 177 km in length and drains into a 1760 km2 watershed area. Four multipurpose dams and many check dams were installed in its upper reach. About 65% of the basin is covered with mountainous landscape, and the remaining 35% is alluvial plain. In the middle reach, the river bed mainly consists of grain, and its width is considerable (about 700 m), but not particularly braided. Due to abundance supply of sediment, natural banks, riverside sand hills, and a wide flood plain formed in the lower middle reach, where the width of the river is smaller (300 m) than it is in the upper middle reach.
The inundated area is a flood plain on the left side of Kinugawa River in the lower middle reach. It is surrounded by a natural levee or sand hill formed by Kinugawa River and Kokaigawa River (Figure 1(c)). The urban area has mainly on a slightly higher elevation. Joso’s city center, called the Mitsukaido area, is also on the higher land, but the residential area has been expanding into the lower flood plain due to population increases. The first inflow of flood water by overtopping occurred in the Wakamiyado area (25.35 km and 24.75 km from Tonegawa River, Figure 2(a)) at 6:30 on Sep. 10 and the Misakacho area (21.0 km from Tonegawa R., Figure 2(b)) at 12:50 by riverbank failure.
A small channel, the Hachikenbori-gawa Channel, lies in the flood plain (Figure 1(c) and Figure 2(c)). It divides the flood plain into east and west sections. The channel was digged for agricultural drainage during the 16th Century. The pumping station, which can drain 30 m3/sec, is installed at the most downstream point of the channel. The channel also branches in the Mitsukaido area, and the sub-channel is called Old Hachikenbori-gawa Channel. Also, several small drainage are installed in the Hachikenbori-gawa Channel, however, many of their gates unintentionally were not closed during the disaster.
2.2. Rainfall
Typhoon No.18 appeared in southern Japan in the northern Pacific (N20˚25'32", E136˚4'52") on September 7, 2015. It moved northward and reached the Atsumi Peninsula, Aichi Prefecture at 10:00 on September 9. Then it became an extratropical typhoon in the Sea of Japan at 15:00. Unfortunately, Typhoon No.17 also retained its intensity in the Pacific Ocean, east of Japan. In combination, the two typhoons brought increasing humidity and forceful winds. As a result, a continuous linear rainfall band that stretched in a north-south direction developed in the North Kanto and Tohoku regions. The accumulated rainfall total
Figure 2. (a) Overtopping at Wakamiyado (25.35 km and 24.75 km), (b) Riverbank failure at Misakacho (21.0 km) and (c) Bank-full water under the flood in Hachikenbori- gawa Channel at Misaka-shinden Station.
was more than 600 mm at Nikko City, Tochigi Prefecture, which is more than twice the mean monthly rainfall. The 24-hour rainfall total at nine stations in Tochigi and Ibaraki Prefectures set new records.
2.3. Injuries and Property Damage
Table 1 presents a summary of the human toll and property damage caused by this disaster. According to this data from the Cabinet Office [7] and local government [8] , the number of deaths and seriously injured people in the Ibaraki Prefecture was three and 51, respectively. In terms of property damage, the
Table 1. Summary of damage and evacuation in Ibaraki Prefecture.
number of partially and fully collapsed buildings, and those with flooding above ground level are 54, 5486, 185 and 3767, respectively. The number of injuries and deaths was not as devastating as in past flood disasters in our history, but the property damage was extensive sewers using several commercial software applications for integrated flood simulation [9] .
2.4. Evacuation
Figure 3 shows time series data of rainfall and evacuation advisories for heavy rainfall (JMA: Japan Metrological Agency), flood disaster (rainfall based, JMA) and specific river flooding (water level based, MLIT: Ministry of Land, Infrastructure, Transport and Tourism) around Joso city. The first heavy-rain advisory was announced on September 8 at 13:29 and it was raised to a heavy rain warning on September 9 at 16:36. A flood advisory was released on September 9 at 5:00 from JMA and it changed to warning at 16:36. In terms of Kinugawa River flood information, MLIT released an advisory at 20:40 on September 9 because the water level at Kinugawa-Mitsukaido Station triggered a flood caution at 23:00, followed by a flood warning at 0:15 on September 10. Approximately six hours later on the 10th, overtopping occurred on the left bank in the Wakamiyado area and flood occurrence information was released at 6:30. After that, an emergency rainfall warning was issued at 7:45, signifying that residents should take immediate survival actions. At 12:50, a left riverbank failure occurred in the Misakacho area. These two severe flooding occurrences inundated the entire flood plain. Joso’s city hall, located in the Mitsukaido area, saw its administrative functions paralyzed.
Finally, an official evacuation directive and an official evacuation call were issued to approximately 34,000 persons. Nonetheless, many residents were stranded in their homes: 1339 persons required rescue by helicopter and 2919 were rescued by boat. Road washouts, railway disruptions and other such transportation complications were the main causes for these extreme measures. Pumping got underway to resolve the inundation, but despite considerable helps, it took about 10 days for the water to recede.
Figure 3. Timeline of disaster-information dissemination in the Kinugawa River basin.
3. Methods
To evaluate the channel’s effect on flooding, we conducted a field survey and integrated hydrodynamic simulation. We investigated the distribution of the inundation depths and levels by measuring hundreds of high water marks using high resolution positioning system called RTK-GNSS (Real-Time Kinematic Global Navigation Satellite System). The geometry of the bank height along the channels was also measured in the field. The 1D/2D coupled hydraulic simulation model was applied to the inundated field for determining the effect of small channels that drive flood water downstream quickly. In this study, MIKE 2016, commercial hydrodynamic simulation software including MIKE FLOOD module capable model coupling of 1D model (MIKE 11) and 2D model (MIKE 21) was used.
3.1. Field Investigation
Field surveys for the investigation of flood characteristics were conducted several times. In the first survey on September 10, the day the flood occurred; we inspected the flood area and found that the initial inundation occurred in the Mitsukaido district, as shown in the photo in Figure 3. Secondary surveys were done to identify flood behavior and characteristics. Many flood marks were measured from the ground to their ultimate height. Some were also measured at their elevation with a portable and high-accuracy positioning system called network type RTK-GNSS with Virtual Reference Station (VRS) method (Trimble R4, Trimble R6 and TOPCON HiPerV GGDM) which has an approximately ±4 cm height margin of error. In this system, initial estimation data are adjusted in real time by information of VRS location and its correction status via mobile phone network. The system also has advantage in portability which is able to treat by one worker and one set of equipment in a few minutes. Although we can obtain flood depth distribution data by conventional way, the new equipment enable to collect absolute level data easily and efficiently and deploy it on GIS software immediately. Finally, we collected 307 and 133 data elements of flood depth and flood elevation including data shared by [10] . To investigate the flooding process, we interviewed area residents and collected their photos of the disaster to extract information of water level under the disaster.
3.2. Numerical Simulation
3.2.1. Governing Equations
The main governing equations of the 1D (MIKE11) and 2D (MIKE21) modules are briefly discussed here, as are the solution procedures. The governing equation of the 1D model is the Saint-Venant equation based on several assumed factors: incompressible and homogeneous fluid, uniform velocity and horizontal water level in cross-section, small bottom slope and small longitudinal variation in hydrostatic pressure distribution. The equations are conservation of mass and momentum as given in Equations ((1) and (2)), respectively.
 (1)
(1)
 (2)
(2)
Solutions of the equations of continuity and momentum are based on an implicit finite difference scheme. The scheme is structured in order to be independent of the wave description specified (i.e., kinematic, diffusive or dynamic). In this simulation, we used a dynamic wave approximation scheme.
The MIKE 21 modelling system is based on the numerical solution of the depth-averaged Navier-Stokes equations describing the conservation of mass and momentum in two horizontal directions. These equations can be written in simplified form as shown in Equations (3) through (5).
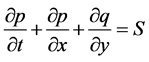 (3)
(3)
 (4)
(4)
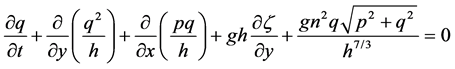 (5)
(5)
These equations are solved using finite difference approximations and an Alternating Direction Implicit (ADI) scheme that include unconditional stability in the linear sense where there is no stability limit on the time step.
To connect the MIKE 11 and MIKE 21 model calculations, we applied the lateral link function in the MIKE FLOOD module, which calculates flow interaction based on the structure equation and water level of MIKE 11 and MIKE 21 on the pre-defined links. Concretely, water levels inside (on 1D) and outside (on 2D) of channel and bank height were compared. If the MIKE 11 water level was higher than the others, the discharge flowing from MIKE11 to MIKE21 was estimated by following Honma’s weir formula, shown in Equation (6). This can more accurately expresses the exchange of volumes via embankment.
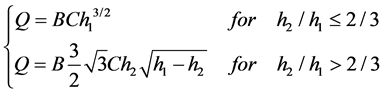 (6)
(6)
Note the flow through the link is distributed into several MIKE 11 computational points to obtain water level h, and the method do not guarantee momentum conservation.
3.2.2. Calculation Setting
As shown in Figure 4(a) and Figure 4(b), the calculation area was set to cover the flooding area. In this calculation we modeled Hachikenbri-gawa Channel and its branches with 1D model and the other field with 2D. Inflow rate onto the 2D field occurred by levee failure and overflowing were considered as boundary conditions. Because of their uncertainty, these inflow input and roughness parameters were calibrated to fit to observed inundation depth and level and water level on the channel. The calculations were carried out from 5:00 on September 10 through 8:00 on September 11 (JST).
In the 2D calculation field, 25,000 (125 × 200) rectangular computational grids (50 m × 100 m) were applied. Needless to say, finer grids or unstructured cells could also provide reliable results; however, it is not necessary and not reasonable in situation like our site that boundary condition remains uncertainty. Flow rate input at the grids for the bank breach (21 km) and overtopping (25 km) were obtained as shown in Figure 4(c) for boundary condition. Overtopping actually occurred at two points, but we considered them as one at 25.0 km. Note that these data are just hypothetical value obtained by following estimation: elongating the observed water level data at near Kamaniwa Station (27.3 km) as the peak attached to the high water mark level at the overtopping and bank breach points, applying the weir formula of Honma and calibrating to fit the maximum depth to the observed in situ flood mark depth. The accumulation of input volume is about 44 million m3, which is similar to the other estimation
Figure 4. (a) and (b) Maps of calculation bathymetry, channel branch, boundary condition and observed inundation depth. Colored mesh and blue lines indicate 2D land height and 1D channel branch location, respectively and colored circles indicate classed high water mark depth. (c) and (d) Time series data of input flow rate for boundary condition onto 2D mesh and 1D region indicating discharge at overtopping and bank collapse points in 2D, and upstream runoff and pumping rate in the 1D model. (e) Model geometry of the 1D model based on level observations using RTK-GNSS.
[10] , however, the inflow data needs further discussion of its validity. The bathymetry for the calculation was obtained by generating 5 m mesh DEM (digital elevation model) data. It is customary to provide a mesh-averaged value, but we took the maximum value −0.6 m to mesh over major road and railway to consider the blocking effects by embankment. Model parameter of roughness, Manning’s n, was set at 0.10 in urban areas and 0.06 which is the range usually used, respectively. Precipitation on the site during the calculation period was ignored because it enough weak (Figure 3).
The 1D open channel model includes Hachikenbori-gawa Channel, Old Hachikenbori-gawa Channel and two small drainage canals attached to the flood plain. Distributed discharge and point sink at the pump station were considered as a boundary condition as shown in Figure 4(d). Initial flow rate and water level were determined to adjust to the condition before the flood water flowing into the channel. The pumping status was decided according to the official report. All the end of the branches was closed, which the mass interaction to 2D region occurred only via the lateral links. The geometry of the 1D branch was based on the observations with RTK-GNSS shown as in Figure 4(e). Manning’s n of the channels and drainage canals was uniformly set at 0.05 considering its vegetation.
4. Results and Discussions
4.1. Model Validation
For model validation, we show results obtained by the 1D/2D coupled model in Figure 5 and Figure 6. Figure 5 shows a comparison between maximum depth in calculation and high water depth obtained by flood mark investigation. The data were stratified into upper, middle and lower areas, shown in Figure 4(a).
Figure 5. Model validations with comparing water depth. The colored marks correspond to the areas displayed in Figure 3.
Figure 6. Time series of observed (marks) and calculated (lines) water level including data analyzed from photos taken under the flood.
The root-mean square of error for the depth estimation was 0.531 m. As a result, the developed model was generally reasonable in whole area. Figure 6 shows a comparison of observation and calculation of water level on the Hachikenbori- gawa Channel. The figure shows time series water levels at Mitsusaka-shinden (blue, 6.9 km from downstream end), the downstream pumping station (red) and Kinugawa River (black, at the Kinugawa-Mitsukaido gauge station, see also Figure 1(c)). The lines indicate calculated values, and marks represent observed values. The yellow hatched marks show the flood-plain water level, gleaned by analysis of pictures and field investigation. Grey hatches show period not including calculations. In upper part of Figure 6, we also display whether pumping was underway. These results confirm that the model provided reasonable output also on 1D region.
4.2. Flooding Process
Figure 7 indicates estimations of water depth and velocity distribution at each time and in maximum given by the 1D/2D coupled model (Figure 7(a)) and the model using 2D instead of 1D part (2D-only) (Figure 7(b)). From the figure, we see that the flooding gradually propagated southward along the Hachikenbori-gawa Channel. Figure 7(a) shows that on September 10 at 11:00, overtopping flow from Wakamiyado reached the right bank of Hachikenbori-gawa Channel and went south along the height bank. At 15:00 after the bank failure, shown in the top middle image of Figure 7(a), the flow from the bank breach point also reached to the Hachikenbori-gawa Channel. The flood entered the channel and
Figure 7. Distributions of depth and velocity in calculation. (a) Results of 1D/2D coupled model and (b) 2D-only model.
partially re-overtopped the left bank. At the same time, we see that small initial flooding happened in the downstream Mitsukaido area and the main flood did not arrive. However, that type of initial inundation could not be identified in the 2D-only model results shown in Figure 7(b).
At 17:00, we found that the main flood moved along the right bank of the channel, and the water depth was higher than that on the left bank. It indicated that the Hachikenbori-gawa Channel bank significantly affected the flood behavior. At 19:00, the flood reached the Mitsukaido area and completely inundated it. On the west side of the Hachikenbori-gawa Channel, where the deepest inundation was observed concequently, the flood had not yet arrived. However, the waters went not only northward upstream, but they also travelled downstream. Between 23:00 and midnight, nearly the entire flood plain was partially submerged, except at the natural levee. Comparing the simulated maximum depth produced by the two models, we did not find any significant difference; however, the existence of a small channel lying on the flood plain changed the flood propagation pattern.
Figure 8 shows time series changes of flood water depth at certain grids in the 1D/2D coupled model (Figure 8(a)) and the 2D-only model (Figure 8(b)) extracted at several meshes shown in Figure 8(c). Here we also found a difference in the initial inundation in the Mitsukaido area, indicated by blue line C and purple line D in Figure 7(a) and Figure 7(b). The 1D/2D coupled model produced a stepwise rising pattern, but the 2D-only model produced a simple gradation. The coupled model showed the start time of the Mitsukaido area flood to be around 14:00, with moderate rises in water depth from 15:00 to 18:00. The 2D-only model, however, does not indicate this. After that, the water depth rapidly increased due to the arrival of the main flood wave at 19:00. In the area on the left side of Hachikenbori-gawa Channel (point E, depicted by the green line) at which maximum inundation depth was observed, the arrival of the flood was
Figure 8. Time series of calculated water depth at certain points on flooded area (a) results of obtained by results of (a) 1D/2D coupled model, (b) 2D-only model and (c) location at which data were extracted.
compared to that of the Mitsukaido area because of blocking by the Hachikenbori-gawa Channel banks. The water depth exceeded 2.0 m in the midnight in calculation, and that coincides with the observations of area residents.
4.3. Flood Diffusion on Channel
As formerly mentioned in Figure 6, the water level at the upstream and downstream stations on the Hachikenbori-gawa Channel rose almost simultaneously at 12:00 indicates the flood wave along the channel quickly diffused downstream. After 15:00, the water-level increase became moderate. At that point, overtopping occurred through the Old-Hachikenbori-gawa Channel and its drainage canals. In fact, the bank height along the Old-Hachikenbori-gawa Channel was lower than the water level then. We were able to reproduce this water level change well with our model.
Photo analysis, shown as yellow-hatched marks in Figure 6, pinpointed the start of inundation in this stage. At that time, flood mark levels on the flood plain were lower than those in the Hachikenbori-gawa Channel, meaning that inflow from the channel to the flood plain actually occurred. After the initial inundation, the flood water level drastically increased at 19:00 due to the arrival of the main flood wave. At this stage, the flood plain was also completely inundated (see also Figure 7). Careful examination showed that the water level on the flood plain was slightly higher than the Hachikenbori-gawa Channel’s water level. This proves that flood water should move from the flood plain to the channels. Moreover, it can be assumed that the Hachikenbori-gawa Channel bank worked to prevent flood waters from flowing into the channel.
4.4. Water Balance Analysis
Mass balance in each channel in the calculation is shown in Figure 9. In this figure, inflow from flood plain to channels is defined as plus. The fluctuating values indicate net volume-per-unit time through each channel in m3/sec unit.
Figure 9. Time series of calculated mass balance across the 1D and 2D connection. Grey hatch indicates out of calculation.
According to the result, about 60 m3/sec inflow into the Hachikenbori-gawa Channel occurred from 11:00 to 15:00. The inflow amount includes the effect of the pumping (30 m3/sec). Thus it can be assumed that the Hachikenbori-gawa Channel actually received about 90 m3/sec of inflow. In the next stage, after 15:00, the total volume gain suddenly decreased because outflow from the Old Hachikenbori-gawa Channel and two small drainage canals began. After the arrival of the main flood wave at 19:00, both inflow into the Hachikenbori-gawa Channel and outflow to the flood plain rapidly increased. The amount of the interaction reached more than 200 m3/sec.
5. Conclusions
In this study, we focused on enhancing of flood diffusion speed by small channel in large floods, and examined the characteristics of disasters occurring in Kinugawa River in Japan in 2015 as a case study. The spatiotemporal change of the flood flooding was investigated by immediate and detailed field survey. We confirmed the initial flooding in the downstream part of the flood zone, which caused by the effect of a small channel. Introducing a handy and highly accurate positioning system, we obtained the spatial distribution of the flooded level from the field survey.
In order to investigate the behaviour of flood waves along small channels, combination of 1D channel flow and 2D flood flow model was applied to the field. The validity of the coupling model was confirmed by inundation depth data and observed water level data. The model estimation provided information that a large amount of floods flowing from the river flow into the small channel in the process of flowing down to lowlands, resulting in a rapid rise in water depth and we also found that a small flood which confused citizens occurred. Comparing the results of the 1D/2D coupled and 2D-only model, it was suggested that the arrival time of the flood is different about 4 hours depending on the considering of the channel even though the 2D-only model provided almost same result in terms of the maximum flooding depth.
The calculation model used in this research is somewhat lower in resolution from the viewpoint of pursuit of reproducibility of flood flow and there are still many unknown points as to the inflow rate at bank breach and overtopping point, which are important condition set. Therefore, this calculation was just a realistic assumption, however, we think that it gives important suggestions for countermeasures against future flood risks as follows; first, it cannot be negligible that influence on the flood diffusion by the existence of a small channel that we usually do not take enough care, and it actually happened. Currently, in our country, as a lesson of such a catastrophe, simulations assuming hyper large floods which its return period is several hundred years or occurring severe bank failure were conducted. This research gives a way of thinking about how much resolution is necessary and what needs to be modelled so that the estimation becomes practically more useful. Secondly, a slight but irregular flooding, as noted in this research, can have a significant influence on the evacuation behaviour of citizens. In fact, since the targeted disaster was an unprecedented scale that had not been experienced before, it is inevitable that the final damage will be enormous to some extent. However, when we take deepen consideration to minimize substantial damage, it is important to organize the direction with a broader perspective on how to deal with the risks associated with the existence of small channels or pipes and how to put them into concrete evacuation strategy.
The problem dealt with in this research is thought to be important in considering the risk of water damage of small aqueducts in two points: phenomenon was relatively simple and it appeared as a real phenomenon rather than simulation. As we could imagine, the risk that we faced on supposed to increase under the more complex urban area in our country [11] . To the increase in the risk of floods due to global warming that is unavoidable in the future much attention should be paid to linear structures such as urban and lowland channel, embankments, and roads.
Acknowledgements
This work was supported by Grants-in-Aid for Scientific Research, KAKENHI, (A, No. 16805896) from the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan. We also acknowledge the Ministry of Land Infrastructure, Transport and Tourism in Japan and the residents of Ibaraki Prefecture for information provided. We are also grateful to Dr. Hiroyuki Nagano, Dr. M.A.C. Niroshinie and all the students of the Hydraulics Laboratory of the Tokyo University of Science for their support, particularly in the field surveys.
Cite this paper
Ohtsuki, K. and Nihei, Y. (2017) Evaluation of Fast Flood Di- ffusion through a Drainage Channel: A Flood Disaster Case Study of Japan’s Kinugawa River, September 10, 2015. Journal of Water Resource and Protection, 9, 1063-1081. https://doi.org/10.4236/jwarp.2017.99070
References
- 1. Domingo, N.S., Refsgaard, A., Mark, O. and Paludan, B. (2010) Flood Analysis in Mixed-Urban Areas Reflecting Interactions with the Complete Water Cycle through Coupled Hydrologic-Hydraulic Modelling. Water Science & Technology, 62, 1386-1392.
http://wst.iwaponline.com/content/62/6/1386 - 2. Leandro, J., Chen, A.S., Djordjevic, S. and Savic, D.A. (2009) Comparison of 1D/1D and 1D/2D Coupled (Sewer/Surface) Hydraulic Models for Urban Flood Simulation. Journal of Hydraulic Engineering, 135, 495-504.
http://ascelibrary.org/doi/abs/10.1061/(ASCE)HY.1943-7900.0000037
https://doi.org/10.1061/(ASCE)HY.1943-7900.0000037 - 3. Tayefi, V., Lane, S.N., Hardy, R.J. and Yu, D. (2007) A Comparison of One- and Two-Dimensional Approaches to Modelling Flood Inundation over Complex Upland Floodplains. Hydrological Processes, 21, 3190-3202.
http://onlinelibrary.wiley.com/doi/10.1002/hyp.6523/abstract
https://doi.org/10.1002/hyp.6523 - 4. Han, K.Y., Lee, J.T. and Park, J.H. (1998) Flood Inundation Analysis Resulting from Levee-Break. Journal of Hydraulic Research, 36, 747-759.
http://www.tandfonline.com/doi/abs/10.1080/00221689809498600
https://doi.org/10.1080/00221689809498600 - 5. Mark, O., Weesakul, S., Apirumanekul, C., Aroonnet, S.B. and Djordjevic, S. (2004) Potential and Limitations of 1D Modelling of Urban Flooding. Journal of Hydrology, 299, 284-299.
https://doi.org/10.1016/s0022-1694(04)00373-7
http://www.sciencedirect.com/science/article/pii/S0022169404003737 - 6. Vanderkrimpen, P., Melger, E. and Peeters, P.L. (2009) Flood Risk Management: Research and Practice: Flood Modeling for Risk Evaluation—A MIKE FLOOD vs. SOBEK 1D2D Benchmark Study. Taylor & Francis, London, 77-84.
- 7. The Cabinet Office, Government of Japan (2016) Summary of Damages by Heavy Rain and Flooding on September, 2015 (2016/2/19 12:00 in Press) (Heisei 27 nen 9 gatsu Kanto-Tohoku Gouu ni yoru higai jokyo tou ni tsuite). [In Japanese]
http://www.bousai.go.jp/updates/h27typhoon18/pdf/h27typhoon18_28.pdf - 8. Ibaraki Prefecture Government (2015) Summary of Damages and Response in Heavy Rain and Flooding on September, 2015 (Heisei 27 nen 9 gatsu Kanto-Tohoku Gouu ni yoru honken no hidai oyobi taiou ni tsuite) (2015/9/29 16:00 in press). [In Japanese]
http://www.pref.ibaraki.jp/1saigai/201509/09291600.html - 9. Ushiyama, M. (2016) Characteristics of Victims of the September 2015 Heavy Rainfall Disaster in the Kanto and Tohoku District. Journal of Japan Society of Civil Engineers Series B1, 72, I_1297-I_1302. [In Japanese with English Abstract]
https://www.jstage.jst.go.jp/article/jscejhe/72/4/72_I_1297/_article/-char/en/ - 10. Sayama, H. and Takara, K. (2016) Estimation of Inundation Depth Distribution for the Kinu River Flooding by 2015.09 Kanto-Tohoku Heavy Rainfall. Journal of Japan Society of Civil Engineers Series B1, 72, I_1171-I_1176. [In Japanese]
https://www.jstage.jst.go.jp/article/jscejhe/72/4/72_I_1171/_article - 11. Sekine, M. and Ikeda, R. (2014) Numerical Simulation of Inundation in Lowland Areas of East Tokyo. Proceedings of Hydraulic Engineering, 70, I_1429-I_1434. [In Japanese with English Abstract]
https://www.jstage.jst.go.jp/article/prohe1990/52/0/52_0_859/_article
Notations
A = flow area (m2)
B = weir width (m)
C = weir coefficient
E = an eddy viscosity coefficient (m2∙s−1)
Q = discharge (m3∙sec−1)
R = hydraulic or resistance radius (m)
S = source or sink term respective to direct inflow (m3∙s−1)
h = water depth (m)
h1 = depth of water above weir level upstream (m)
h2 = depth of water above weir level downstream (m)
n = Manning’s roughness coefficient (m−1/3∙s−1)
q = lateral inflow per unit width (m2∙s−1)
t = time (s)
u, v = depth averaged velocities in x and y directions (m∙s−1)
x, y, z = space coordinate (m)
α = momentum distribution coefficient (-, = 1.0)
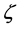 = free surface elevation (m)
= free surface elevation (m)

Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact jwarp@scirp.org











