Positioning
Vol.06 No.01(2015), Article ID:53426,5 pages
10.4236/pos.2015.61001
PPP Accuracy Enhancement Using GPS/GLONASS Observations in Kinematic Mode
Mahmoud Abd Rabbou, Ahmed El-Rabbany
Department of Civil Engineering, Ryerson University, Toronto, Canada
Email: mahmoud.abdelrahman@ryerson.ca
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 January 2015; accepted 19 January 2015; published 21 January 2015
ABSTRACT
Commonly, kinematic PPP techniques employ un-differenced ionosphere-free linear combination of GPS observations. This, however, may not provide continuous solution in urban areas as a result of limited satellite visibility. In this paper, the traditional un-differenced as well as between-satel- lite single-difference (BSSD) ionosphere-free linear combinations of GPS and GLONASS measurements are developed. Except GLONASS satellite clock products, the final precise GPS and GLONASS satellites clock and orbital products obtained from the multi-GNSS experiment (MGEX) are used. The effects of ocean loading, earth tide, carrier-phase windup, sagnac, relativity, and satellite and receiver antenna phase-center variations are rigorously modeled. Extended Kalman filter (EKF) is developed to process the combined GPS/GLONASS measurements. A comparison is made between three kinematic PPP solutions, namely standalone GPS, standalone GLONASS, and combined GPS/ GLONASS solutions. In general, the results indicate that the addition of GLONASS observations improves the kinematic positioning accuracy in comparison with the standalone GPS PPP positioning accuracy. In addition, BSSD solution is found to be superior to that of the traditional un-diffe- renced model.
Keywords:
GPS, GLONASS, PPP, Kalman Filter (KF)

1. Introduction
Precise point positioning (PPP) can potentially achieve centimeter- and decimeter-level accuracy in static and kinematic modes, respectively, depending on the number and geometry of visible GPS satellites, and quality of observations. This, however, may not be the case in urban areas, as the satellite visibility may be limited. To overcome this limitation, we propose to combine the observation of GPS and GLONASS systems. The additional GLNOASS observations are expected to enhance the PPP accuracy and solution availability, especially in dense urban areas where, in general, no sufficient number of GPS satellites are visible.
We take advantage of the full GLONASS constellation and the availability of precise orbital and clock products produced by number of organizations, such as International GNSS Service (IGS). However, the difference between signal structures of the two systems is still creating some difficulties in the combined model implementation. Fortunately, Russia is planning to add Code Division Multiple Access (CDMA) signals to the Frequency Division Multiple Access (FDMA) used in the current GLONASS satellites signals, which facilitate and improve the combined use of GPS and GLONASS ( [1] ). In addition, some researchers developed PPP models for combined GPS/GLONASS observations using un-differenced ionosphere-free technique ( [2] and [3] ). Their results showed an improvement in the positioning accuracy by adding GLONASS observations to the kinematic PPP with a limited number of available GPS satellites. However, the results showed that the contribution of adding GLONASS satellites on positioning accuracy was not sufficient for the daily static PPP considering enough available GPS satellites with good geometry.
In this paper, the combination between GPS and GLONASS observations is investigated for kinematic applications, based on recent advances in PPP algorithms that implement both un-difference and between-satellite- single-difference BSSD ionosphere-free linear combinations. Except GLONASS satellite clock products, the final precise GPS and GLONASS satellites clock and orbital products obtained from the multi-GNSS experiment (MGEX) are used herein ( [4] ). Three PPP solution cases are considered in this paper, namely GPS-only PPP solution, GLONASS-only PPP solution, and combined GPS/GLONASS PPP solution. The performance of the PPP accuracy of each case is assessed by comparing it with the carrier phase-based differential GNSS (DGNSS) solution.
2. GPS-GLONASS BSSD Ionosphere-Free Model
The un-differenced ionosphere-free combination of code pseudorange and carrier phases is the widely used PPP model ( [5] ). Its mathematical model can be written as;
 (1)
(1)
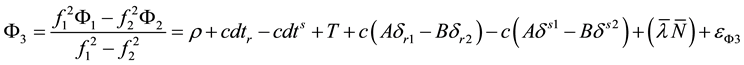 (2)
(2)
where  and
and  are pseudorange measurements on
are pseudorange measurements on 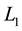 and
and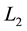 , respectively;
, respectively; 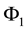 and
and 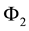 are the carrier phase measurements on
are the carrier phase measurements on 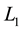 and
and , respectively;
, respectively; 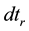 and
and 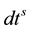 are the clock errors for receiver and satellite respectively;
are the clock errors for receiver and satellite respectively;  and
and 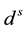 are frequency-dependent code hardware delay for receiver and satellite, respectively;
are frequency-dependent code hardware delay for receiver and satellite, respectively;  and
and 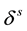 are frequency-dependent carrier phase hardware delay for receiver and satellite, respectively;
are frequency-dependent carrier phase hardware delay for receiver and satellite, respectively;






are frequency dependent factors 


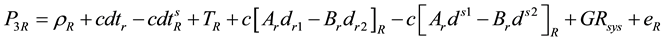


where GRsys is the time offset between GPS and GLONASS. After arrangements, Un-differenced ionosphere-free linear combination equations can be simplified to;




where IFCB is un-differenced ionosphere code bias, IFPB is un-differenced ionosphere-free phase bias, ISCB is inter-system code bias, 







It can be clearly seen the receiver related biases and clock errors are eliminated by satellite single difference technique. However, in contrast with GPS, due to the dissimilarities between GLONASS satellites frequencies, receiver related bias residuals may be still exist refers to Frequency-channel biases. These biases, like un-diffe- renced technique, will be lumped to the GLONASS ambiguities.
3. GPS-GLONASS PPP Measurements Filtering
Extended Kalman filter (EKF) is employed to process GPS and GLONASS measurements as presented in ([6] ). GPS and GLONASS raw pseudorange and phase observations are processed to produce estimates of the EKF state vector. MGEX-IGS precise orbital and clock products are used to eliminate satellite orbit and clock errors. However, Due to the unavailability of GLONASS satellite clock product provided by MGEX for the test day, the traditional IGS GLONASS clock products are used herein. The UNB3 tropospheric model consisting of the Saastamoinen vertical propagation delay model and the Niell mapping function is used to account for the tropospheric wet and dry components ( [7] ). The effects of ocean loading, earth tide, carrier-phase windup, sagnac, relativity, and satellite antenna phase-center variations are rigorously modeled [8] . The estimation state vector consists of the three GNSS receiver positioning (latitude, longitude and altitude), receiver clock, GPS/GLONASS internal system bias and the float ambiguity parameters. Two mainly steps are applied on EKF, namely prediction step and update step which can be described as.
The prediction step:


The update step:



where 








4. Test Results and Analysis
A vehicular test was conducted to evaluate the performance of the developed combined GPS/GLONASS-PPP models. The test was carried out in the downtown core of Kingston, Ontario, on December 12, 2012 (DOY 347), under challenging scenarios for satellite navigation availability (Figure 1). Trimble GNSS R10 receiver was employed to collect the kinematic GNSS observations. The positioning accuracy is assessed referenced to carrierphase-based differential GNSS (DGNSS) solution. In order to create this reference solution, a Trimble R7 GNSS receiver was setup at a station with precisely known coordinates, which was considered as a base station. The raw dual-frequency GNSS pseudorange, and carrier phase observations were collected at a 1 Hz rate.
Figure 2 illustrates the GNSSPPP positioning accuracy for the un-differenced and the BSSD ionosphere-free PPP algorithms, respectively, for Kingston trajectory on DOY 347, 2012. Three GNSS solutions are considered, namely the GPS-only and GLONASS-only and, combined GPS/GLONASS PPP solutions. As can be seen, both un-differenced and BSSD ionosphere-free PPP algorithms show decimeter-level positioning accuracy. However, it can be seen that the accuracy of BSSD ionosphere-free model is better than that of un-differenced model of GPS-only PPP and GNSS-PPP while no significant improvements for GLONASS-PPP. This is attributed to the fact that each GLONASS satellite had different receiver biases due to the dissimilarities of satellites frequency, which cannot be completely canceled out using single satellite difference. Also, it can be clearly seen that the accuracy of GLONASS PPP solution is lower than that of GPS PPP solution. This is attributed to the lower number of visible GLONASS satellites compared with those of GPS. The positioning accuracy was improved by adding GLONASS observations in the combined GPS/GLONASS models. However, the solution improvement is not consistent over time and depends on the availability of sufficient number of GPS satellites.
To assess the positioning accuracy of the developed PPP models, Table 1 shows some statistical parameters, including the maximum, minimum, mean and root mean square errors (RMSE) for the various GNSS model combinations referenced to carrier phase-based DGNSS solution. By comparing the mean and the RMSE of all GNSS model combinations, it can be seen that the positioning accuracy is generally improved when GLONASS observations are added. Also it can be seen that the positioning results of BSSD model are more accurate than that of the traditional un-differenced model.
Figure 1. GNSS visible satellites during the trajectory tests.



Figure 2. Positioning accuracy for un-differenced and BSSD ionosphere-free PPP techniques using GPS only, GLONASS only and GPS & GLONASS.
Table 1. Statistical parameters for various GNSS model combinations.
5. Conclusion
The performance of combined GPS/GLONASS PPP model in kinematic mode has been investigated. Three GNSSPPP models have been considered, namely GPS-only and GLONASS-only and, combined GPS/GLONASS PPP. It has been shown that utilizing BSSD ionosphere model enhances the positioning accuracy generally in the standalone GPS and the combined GPS and GLONASS-PPP, while no significant improvements in the GLONASS-PPP is shown. GLONASS-PPP positioning solution shows that positioning accuracy is less than the GPS PPP due to the limited number of GLONASS satellites available compared with GPS. The results also clearly show the addition of GLONASS satellites observations generally improved the positioning accuracy compared to GPS only PPP.
References
- Gibbons, G. (2008) Russia Approves CDMA Signals for GLONASS, Discussing Common Signal Design. Inside GNSS.
- Cai, C. and Gao, Y. (2007) Precise Point Positioning Using Combined GPS and GLONASS Observations. Positioning, 1, 0.
- Choy, S., Zhang, S., Lahaye, F. and Héroux, P. (2013) A Comparison between GPS-Only and Combined GPS + GLONASS Precise Point Positioning. Journal of Spatial Science, 58, 169-190. http://dx.doi.org/10.1080/14498596.2013.808164
- Weber, R. (2012) The IGS Multi-Signals Tracking Campaign MGEX-Planning, Status, Perspectives. In IGS Workshop 2012, 23-27.
- Hofmann-Wellenhof, B., Lichtenegger, H. and Wasle, E. (2008) GNSS Global Navigation Satellite Systems; GPS, GLONASS, GALILEO & More. Springer, Vienna.
- Jekeli, C. (2001) Inertial Navigation Systems with Geodetic Applications. Walter de Gruyter. http://dx.doi.org/10.1515/9783110800234
- Leandro, R., Santos, M.C. and Langley, R.B. (2006) UNB Neutral Atmosphere Models: Development and Performance. In ION NTM, 18-20.
- Kouba, J. (2009) A Guide to Using International GNSS Service (IGS) Products. International GNSS.
- Elsobeiey, M. and El-Rabbany, A. (2014) Efficient Between-Satellite Single-Difference Precise Point Positioning Model. Journal of Surveying Engineering, 140, Article ID: 04014007. http://dx.doi.org/10.1061/(ASCE)SU.1943-5428.0000125
- Abd Rabbou, M. and El-Rabbany, A. (2014) Tightly Coupled Integration of GPS Precise Point Positioning and MEMS-Based Inertial Systems. GPS Solution. http://dx.doi.org/10.1007/s10291-014-0415-3







