Engineering
Vol.10 No.02(2018), Article ID:82762,8 pages
10.4236/eng.2018.102004
Predicting the Permeability of Fractured Porous Rock
Wenjing Lu1, Haojiao Liu2,3
1Middle School Attached to University of Beijing Jiaotong, Beijing, China
2University of Chinese Academy of Sciences, Beijing, China
3Institute of Mechanics, Chinese Academy of Sciences, Beijing, China

Copyright © 2018 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: January 3, 2018; Accepted: February 25, 2018; Published: February 28, 2018
ABSTRACT
Fractures are widely distributed in tight reservoirs. Fractures and pore-throats form the flow path of oil/gas/water in reservoirs. How to determine the permeability of fractured porous reservoirs is still difficult. A group of tight sandstone samples are first used to measure the fractures and analyze the distribution rules between numbers and length, angles. The permeability changing with the fracture’s length and density for different matrixes is then computed by using pore-fracture network model. At last an empirical formula for predicting the permeability related with the fracture’s length and density is fitted based on the computed data.
Keywords:
Permeability, Fractured Porous Rock, Network Model

1. Introduction
Permeability of fractured porous rock is important but difficult to predict because of the complex fracture distribution and pore-throat characteristics. Fracture network strongly affects the seepage properties of rocks, such as oil/gas reservoirs. But how to evaluate the effects of fractures on the permeability of porous media is still very difficult. Many methods have been presented for predicting the permeability but each has a scope of application. So the prediction of permeability of fractured porous media is still required to study.
Lorente et al. [1] studied the characteristics of fractured porous media. Their results show that this kind of media is multi-scale. Warren and Root [2] and Koudina et al. [3] assumed that a fractured system in a porous rock is consisted of identical rectangular porous parallel pipes. Flow takes place in the fracture network which is fed by the porous blocks. These studies show that the fracture’s average length and density have great effects on the permeability. Though the study can reflect some phenomenon of seepage in rocks, the assumption of rectangular porous parallel pipes is deviated from the real ones. Liu [4] presented a formula for predicting the permeability of fractured shale rock based on the fractal theory. This formula considered the curved fractures and variable width, but it is very complex. Liu and Fan [5] adopted superposition algorithm to calculate the equivalent permeability tensor for multiple sets of infinity parallel fracture. The method can consider the length variation, but the permeability must be computed by numerical simulation.
Pore-fracture network model has also been used to analyze the permeability of the fractured porous rock. This model has many advantages. For example, it can easily model the effects of different fracture’s and pore-throats distribution. The micro displacement and macro seepage characteristics can also be easily solved [6] [7] . Thus this method is used in the following analysis.
The scaling of fractures in rock has been implied widely in tectonics, seismic hazard assessment etc. It is shown that distribution of fractures in many kinds of rocks can be described by power-law scaling [8] [9] . The seepage characteristics and parameters are studied and predicted based on this distribution law.
In this paper, fractures in a group of tight sandstone samples are measured and used to examine is the fracture distribution satisfies the power-law scaling. Then the permeability changing with fracture’s length and density for different matrix is computed by using pore-fracture network model. An empirical formula is presented for predicting the permeability of fractured porous rock at last.
2. Power Law Scaling of Fractures
Previous study shows that the cumulative number of fractures (N) having length ≥ L can be expressed as [9]
(1)
in which A and B are coefficients.
The tight sandstone samples were selected from typical oil formation in Sichuan province to analyze the statistical characteristics of the fractures. The Sichuan Basin is the greatest potential area for oil/shale gas production in China. Fuling District in Chongqing city, aiming Longmaxi formation, has realized breakthroughs. The tight sand samples have a length of 12 cm and diameter of 6 cm. 12 samples were used to measure and analyze the fractures (Figure 1). The fractures are measured by rules, protractor and magnifier, the width is too small to measure and only the fractures with length more than 5 mm are measured.
The data between the fracture length and the accumulated numbers are drawn in Figure 2. It is shown that these two factors can be described by power-law scaling. Most fractures are with angles in the range 90˚ - 135˚ (Table 1). That means, the fractures are close to the vertical direction. The samples are finite because they are difficult to obtain. However, the scaling law between the
Figure 1. Photos of samples (The left is the samples. The right shows the fractures). (a) Samples; (b) Fractures at the surface.
Figure 2. Relation between fracture length and fracture number.
Table 1. Number of fractures in different range of angles (Horizontal line is 0˚ or 180˚).
fracture length and numbers is similar to the previous results [9] [10] .
It can be thought that the permeability changes with fracture’s characteristic parameters based on the permeability of matrix. That means, the permeability of fractured porous rock can be expressed as the product of the permeability of matrix and a function related with the characteristic parameters of fractures. Generally, average length and density can be taken as the characteristic parameters of fractures [11] [12] . For a power-law type fracture system, the average length and density can be computed in the following way.
Equation (1) can be rewritten as the following dimensionless form:
(2)
in which Nm is the total of fractures, Lm is the maximum of fracture length, a and b are coefficients. Considering the fractures distribute in an area S, the average length and density can be solved as follows.
The average length of fractures Nf by integrating Equation (2) and divided by Nm:
(3)
The density of fractures Da:
(4)
For other type of distributed fractures, the fracture’s length and density can be obtained in the similar way.
In the next sections, the permeability is computed by using the pore-fracture network model. A fitting relation between the permeability and the average fracture’s length and density is obtained based on the computed data. As an example, the width of the fractures and the direction angle are assumed to be constant.
3. Computation of Permeability by Using Pore-Fracture Network Model
1) Introduction of pore-fracture network model.
Pore-fracture network model (PFNM) is consisted of pores, throats and fractures (shown in Figure 3). Each pore is connected with four neighboring pores by four cylindrical throats respectively. Pores are large and act as inner storage space, while throats are narrow and long channel for flow. Fractures are longer and wider than throats. Each fracture connects two nonadjacent pores. Flow in
Figure 3. Sketch of PFNM.
throats and fractures is assumed to satisfy the Poiseuille equation. The equation system of pore pressure is built by the zero total flow rate at each pore because of the incompressible pore fluid. The pore pressure can be obtained by the built equation system. The driving power is the pressure different between the two ends of any throat or fracture. Based on the solved pressure, the flow velocity, permeability can be obtained [13] .
Pores and throats are assumed to be in normal distribution. For randomly distributed fractures’ angles, the angles can be thought as uniform in the three directions respectively. So the fractures’ directions are set to be horizontal considering the displacement direction in the following simulation. In this paper, we only discuss the changing of permeability with fracture’s length and density.
The controlling equation of single phase flow in throats:
(5)
where q is the flow rate, μ is the dynamic viscosity of fluid, ρ is the density of fluid, p is the pore pressure.
Considering the incompressibility of the fluids (oil and water), the flow rate must be zero at each pore. The total flow rate at each pore is:
(6)
Substituting Equation (5) into Equation (6) yields:
(7)
By solving the above equations, the pore pressure at each pore can be obtained.
The absolute permeability of a single fluid phase in the network can be calculated by the Darcy’s law and the solved pore pressure:
(8)
where μ is the viscosity of fluid, L is the length of network, A is the area of cross sectional.
4. Computing Results
The existence of fractures in fractured porous rock leads to a great change in the permeability. Effects of the length and the number of the fractures are investigated. Two kinds of matrix with different permeabilities are considered.
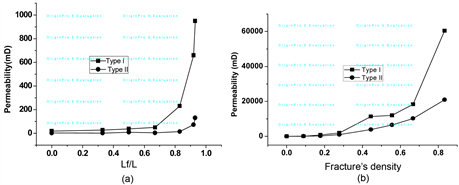
The absolute permeability increases with average fracture length and fracture density (Figure 4) and presents a sharp increase when lf/l exceeds 0.8. In this case, channeling occurs. The absolute permeability of type I rock increases faster than that of type II. The reason is that the permeability of matrix of type I rock is larger, so the fractures present larger effects at the same fracture’s length because more fluids can flow through in the same fracture.
According to the above data, the fitting relation can be expressed as follows:
For type I rock: (9)
For type II rock: (10)
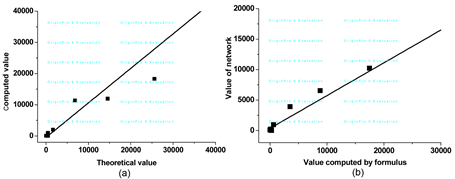
From Equations (9) and (10), it can be seen that the effects of average length are larger than that of density. For type I rock, the effects of density can be neglected. The increase of average length of fractures can fast strengthen the connectivity of rock. The larger the initial permeability is, the more obvious the effects are. The predicted absolute permeability is computed first by the above two Equations (9) and (10) and the data in Table 2. Then the predicted data are compared with that computed by the pore-fracture network model. It is shown that the two sets of data are agreement well with each other (Figure 5). Thus, the presented formulation for prediction of permeability is reliable in the range of discussion. By the data in Figure 1, the permeability computed by Equation (9)
Figure 4. Influences of fracture’s length and density on the absolute permeability. (a) The influences of fracture; (b) The influences of the number of length on absolute permeability fractures on absolute permeability.
Figure 5. Comparison of theoretical and computed values. (a) Comparison of theoretical and computed values under case I (relative error 95%); (b) Comparison of theoretical and computed values under case II (relative error 98.3%).
Table 2. Network parameters of different type.
is 2 mD, which is close the measured data 3 mD. Though the presented formula catch the main factors and is simple for use in practical engineering, some factors (fracture width and three dimensional distribution etc.), can also affect the permeability in some cases, are not considered. The fracture system in the real rock is complex, thus much deeper work is required to do to build a more practical prediction formula.
5. Conclusions
To seek an appropriate method for predicting the absolute permeability of fractured porous rock, fracture distribution was first discussed. Then the pore-fracture network model was used to analyze the absolute permeability under different conditions (matrix, fracture’s length and density). An empirical method for determining the permeability of fractured porous rock is presented. It is shown that the permeability increases non-linearly with fracture’s length and density for different matrixes. The absolute permeability of the rock with fractures distribution can be expressed as a function of the permeability of matrix and fracture’s length and density.
Though the main factors are considered in the presented formula and the form is simple, Fracture width and spatial distribution which can also affect the permeability in some cases are not considered. Much deeper work is required to do to build a more practical prediction formula.
Cite this paper
Lu, W.J. and Liu, H.J. (2018) Predicting the Permeability of Fractured Porous Rock. Engineering, 10, 35-42. https://doi.org/10.4236/eng.2018.102004
References
- 1. Lorente, S. and Bejan, A. (2006) Heterogeneous Porous Media as Multi-Scale Structures form Maximum Flow Access. Journal of Applied Physics, 100, 1149091-1149098. https://doi.org/10.1063/1.2396842
- 2. Warren, J.R. and Root, P.J. (1963) The Behaviour of Naturally Fractured Reservoirs. Society of Petroleum Engineers, 228, 245-255. https://doi.org/10.2118/426-PA
- 3. Koudina, N., Gonzalez, G.R. and Thovert, J.F. (1998) Permeability of Three-Dimensional Fracture Networks. Physical Review E, 57, 4466-4479. https://doi.org/10.1103/PhysRevE.57.4466
- 4. Liu, H.P. (2017) Fractal Seepage Characteristics of Triple-Medium Shale Gas Reservoirs. Sino-Global Energy, 22, 26-31. (In Chinese)
- 5. Liu, Q.Q. and Fan, H.G. (2012) An Approximate Method for Calculating the Equivalent Permeability Tensor of Seepage in Complex Fractures. Mechanics in Engineering, 34, 16-20. (In Chinese)
- 6. Fatt, I. (1956) The Network Model of Porous Media, I. Capillary Pressure Characteristics. Transaction of American Institute of Mining, Metallurgical, and Petroleum Engineers (AIME), 207, 144-159.
- 7. Deng, S.G., Lu, L., Liu, H.J., et al. (2015) Pore Fractural Network Model for Compacted Geomaterials and Simulation of Shale Gas Seepage. Chinese Journal of Underground Space and Engineering, 11, 76-79. (In Chinese)
- 8. Cowie, P.A., Knipe, R.J. and Main, I.G. (1996) Scaling Laws for Fault and Fracture Populations—Analyses and Applications. Journal of Structural Geology, 18, 135-383.
- 9. Marrett, R. (1996) Aggregate Properties of Fracture Populations. Journal of Structural Geologym, 18, 169-178. https://doi.org/10.1016/S0191-8141(96)80042-3
- 10. Marrett, R., Ortega, O.J. and Kelsey, C.M. (1999) Extent of Power-Law Scaling for Natural Fractures in Rock. Geology, 27, 799-802. https://doi.org/10.1130/0091-7613(1999)027<0799:EOPLSF>2.3.CO;2
- 11. Zhang, X.H., Zheng, W., Liu, Q.J., et al. (2014) Algorithm Implementation of Dual-Percolation Model for Fractured Pore Media. Chinese Journal of Computational Physics, 31, 118-126. (In Chinese)
- 12. Bogdanov, I.I., Mourzenko, V.V. and Thovert, J.F. (2003) Effective Permeability of Fractured Porous Media in Steady State Flow. Water Resources Research, 39, 1023. https://doi.org/10.1029/2001WR000756
- 13. Liu, H., Zhang, X., Lu, X., et al. (2017) Study on Flow in Fractured Porous Media Using Pore-Fracture Network Modeling. Energies, 10, 1984. https://doi.org/10.3390/en10121984