Engineering
Vol. 2 No. 12 (2010) , Article ID: 3603 , 4 pages DOI:10.4236/eng.2010.212118
Classical and Fractional-Order Analysis of the Free and Forced Double Pendulum
Department of Aeronautical Engineering, Faculty of Aeronautical and Astronautical Engineering, Istanbul Technical University, Maslak, Istanbul, Turkey
E-mail: anli@itu.edu.tr, ozkol@itu.edu.tr
Received August 11, 2010; revised October 8, 2010; accepted November 23, 2010
Keywords: Double Pendulum, Fractional Dynamics, Lagrangian Dynamics
ABSTRACT
This paper presents the fractional-order dynamics of the double pendulum by means of fractional-order modeling. Equations of motion have been derived for cases with and without external forcing. Generalized force terms have been obtained for five different cases of forcing. Both integer and fractional-order analysis have been carried out. Phase diagrams have been plotted to visualize the effect of fractional order approach. The originality of this work arises from the fact that the double pendulum has been modeled with the fractional dynamics approach. The governing equations of motion of the system have been obtained through fractional variational principles.
1. Introduction
The double pendulum is a system made of a simple pendulum attached to the end of another simple pendulum, displaying rich dynamic behavior (Figure 1). The motion of a double pendulum becomes chaotic above a certain energy level. It has attracted the attention of many researchers due to its complex behavior, including chaotic behavior. A close inspection at a simple mechanical system such as the double pendulum exhibits a remarkable variety of motions. By examining its dynamics with and without an external force, the system gives the researcher essential ideas of linearity and non-linearity, including chaos. Some important properties and constants which can be measured in systems characterized as “pendulum type systems” are gravitational constant, viscosity, attraction of charged particles and time. Besides, some of the classical, chaotic and quantum dynamics concepts, such as period, frequency, resonance, conservation of energy, conservation of angular momentum, forcing, harmonic motion, dissipation, damping, linearization assumption, Fourier spectra, bifurcation, period doubling, nonlinearity, chaotic behavior, phase diagrams, Poincare maps, fractal structures, the Lorentz attractor, quantum pendulum, duality, probability amplitude, uncertainty and the discrete energy spectrum, can all be easily defined through the dynamics of a pendulum. The preceding reasons are quite enough to make the pendulum dynamics attractive.
Advances in high capacity computer technology and non-linear dynamics turn the attention of scientists and engineers to fractional variational principles, due to their various applications in many fields of science and engineering, including dynamics, fluid flow, rheology, diffusion phenomena, electromagnetic theory, electrical networks and probability. Application of fractional-order dynamics in these fields can be found in open literature, however the trend seems that hardly any field in science or engineering has remained untouched by the fractional approach.

Figure 1. The double pendulum.
The double pendulum has attracted the interest of many researchers due to its remarkable dynamics as a prominent example of transition to chaos, despite its simple structure. The characteristics of its motion change signifycantly as its energy level increases. The forces in the double pendulum system have been computed in [1] and periodic, quasi-periodic and chaotic orbits have been identified. Existence of irregular vibrations and both periodic and chaotic trajectories of a mathematical double pendulum system is proven in [2]. Stabilization of a double pendulum with an elastic motor shaft in inverted position is achieved experimentally in [3]. The nonlinear response of a three degree of freedom vibratory system with a double pendulum in the neighborhood of internal and external resonances is investigated. It is stated that one mode of vibration may excite or damp another in such systems, and there may appear chaotic vibrations along with different kinds of periodic vibrations in [4]. The analogy between a double pendulum and an oscillating electrical system is established in [5] and the chaotic regime of the circuit is studied. The numerical analysis of chaos in [6] confirms the passing of the system from regular low-energy motion into chaos as energy is increased, by making use of bifurcation diagrams, Poincare sections and Lyapunov exponents.
Fractional calculus extends differentiation and integration from integer-order space into fractional space. Fractional-order modeling describes various physical phenomena such as viscoelasticity, diffusion, polarization or electromagnetic waves. Fractional dynamics has gained increasing popularity by researchers over the years. In the case of oscillatory problems or the dynamics of a pendulum, what is generally done is that systems are modeled using classical integer-order approach, and then some of the integer-order differential terms are replaced by fractional-order differentials, instead of modeling the system directly and completely using fractional approach. For example, in [7] the damping term of the Duffing equation is replaced by a fractional derivative, and then the chaotic dynamics of the system has been examined. Likewise, Duffing’s equation is cast into a set of firstorder differential equations in [8], and then the conventional derivative expressions are replaced by fractional derivatives. In the same manner, classical time derivatives in the state space equations of the Van der Pol oscillator are replaced by fractional ones in [9]. Fractional damping has also been applied to a pendulum system in [10].
In this study, the dynamics of the double pendulum has been modeled using fractional dynamics approach. In order to show the similarities and differences between the solution sets, both classical and fractional modeling approaches are applied to the double pendulum problem. Classical integer-order and fractional-order modeling of the double pendulum are carried out under five different forcing conditions and three sets of initial conditions. Generalized forces have been obtained for each case of forcing, which are horizontal, vertical, and axial forcing at the tip of the second arm, vertical forcing through the center of gravity of the second arm, and the generalized case of forcing. Effects of fractional order modeling on the dynamics of the double pendulum are observed and presented visually through trajectory diagrams and phase diagrams in Section 7.
The organization of this paper is as follows. Equations of motion of the free, integer-order double pendulum are derived in Section 2. Fractional calculus is introduced and equations of motion are derived through fractional principles in Section 3. Generalized force terms related to each case of forcing are derived in Section 4. Terms derived in Sections 2-4 are combined to give the global equations of motion in Section 5. Initial conditions used in the calculations are given in Section 6. Diagrams and results are given in Sections 7 and 8.
2. Double Pendulum and the Equations of Motion
Equations of motion of the double pendulum can be derived using Lagrange’s equation
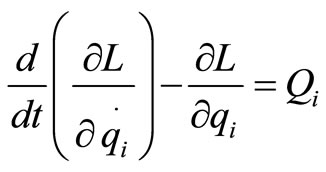 (1)
(1)
where 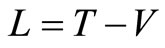 is defined as the Lagrangian of the system,
is defined as the Lagrangian of the system,  is the kinetic energy, and
is the kinetic energy, and 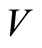 is the potential energy of the system. The motion of the double pendulum has two generalized coordinates,
is the potential energy of the system. The motion of the double pendulum has two generalized coordinates, 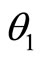 and
and , as seen in Figure 1, resulting in two equations of motion pertaining to the dynamics of the double pendulum.
, as seen in Figure 1, resulting in two equations of motion pertaining to the dynamics of the double pendulum.
It should be noticed that the generalized force  when there is no external forcing function. The Lagrangian of the double pendulum in terms of the generalized coordinates
when there is no external forcing function. The Lagrangian of the double pendulum in terms of the generalized coordinates 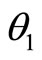 and
and 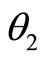 is
is
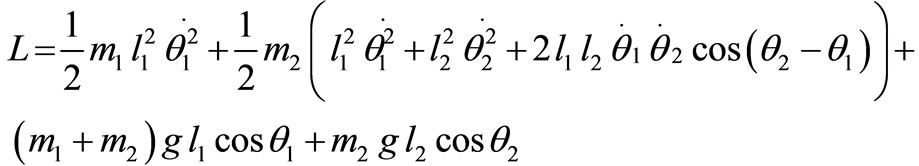 (2)
(2)
where 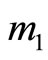 and
and  are the masses of the pendulum bobs located at points
are the masses of the pendulum bobs located at points  and
and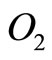 , respectively,
, respectively, 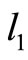 is the distance
is the distance ,
, 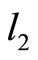 is the distance
is the distance ,
, 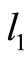 and
and  are inextensible elements and
are inextensible elements and is the gravitational acceleration. Substituting Equation (2) into Equation (1) yields the equations of motion of the double pendulum.
is the gravitational acceleration. Substituting Equation (2) into Equation (1) yields the equations of motion of the double pendulum.
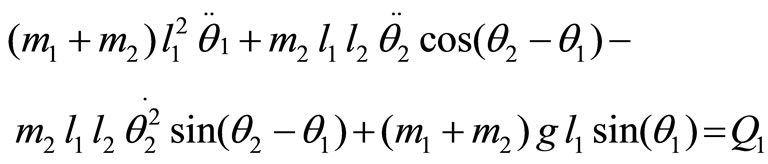 (3)
(3)
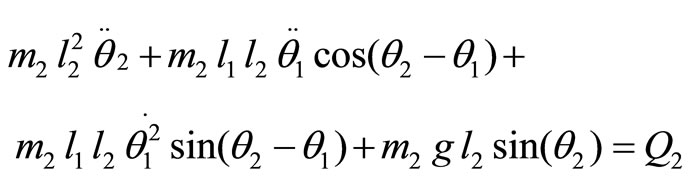 (4)
(4)
where 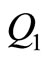 and
and 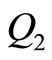 are the generalized forces which will have nonzero values in the case of external forcing and vanish otherwise.
are the generalized forces which will have nonzero values in the case of external forcing and vanish otherwise.
3. Fractional Calculus and Derivation of the Fractional Terms
Fractional calculus refers to generalization of derivatives and integrals into fractional, non-integer orders. The advantage of fractional calculus over classical integer-order calculus is that fractional-order derivatives describe the memory of a dynamical system. Interestingly, in relativistic mechanics, the motion of material objects is not always in three dimensions, it rather depends on restraint conditions. Researchers have extended integer space into fractional space as the dimension of space plays an important role in areas such as quantum field theory and Casimir effect. Even more interestingly, the dimension of the real world was measured experimentally and found to be 3 ± 10-6. This is in accordance with general relativity that gravitational fields are curvatures in space-time, instead of being entities in a flat space-time [11].
There are several definitions of fractional derivatives, like Grünwald-Letkinov, Riemann-Liouville or Caputo formulations [12]. Right and left Riemann-Liouville fractional derivatives are [13], respectively
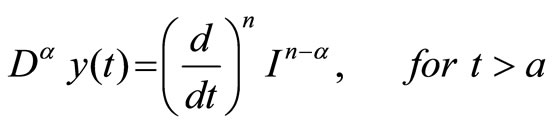 (5)
(5)
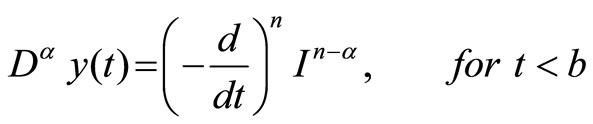 (6)
(6)
where , fulfilling the condition
, fulfilling the condition , is the fractional order,
, is the fractional order, 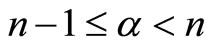 and
and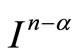 terms are the Riemann-Liouville fractional integrals. It should be noted that replacing
terms are the Riemann-Liouville fractional integrals. It should be noted that replacing  with 1 gives classical integer-order derivatives.
with 1 gives classical integer-order derivatives.
Riemann-Liouville fractional integrals are given as
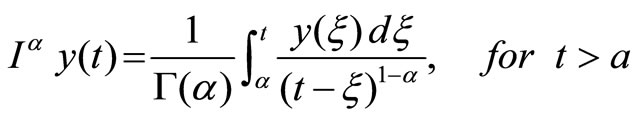 (7)
(7)
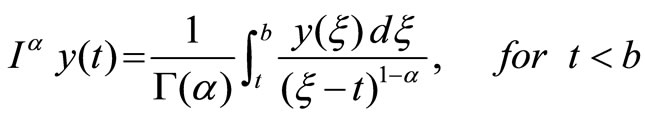 (8)
(8)
where 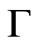 is the gamma function. For a Lagrangian function defined as
is the gamma function. For a Lagrangian function defined as 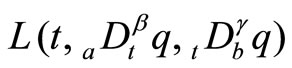 [11] where
[11] where  and
and 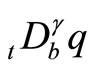 denote the right and left fractional integrals of order
denote the right and left fractional integrals of order 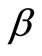 and
and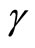 , respectively, and
, respectively, and 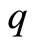 denotes the generalized coordinates, the Euler-Lagrange equations of motion for the unforced system are
denotes the generalized coordinates, the Euler-Lagrange equations of motion for the unforced system are
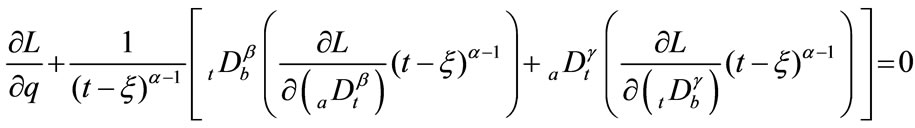 (9)
(9)
By definition, the Lagrangian is evidently obtained in terms of integer-order derivatives. Thus, it would be logical to substitute 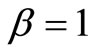 and
and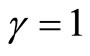 . Moreover, the Lagrangian depends only on
. Moreover, the Lagrangian depends only on  or
or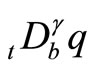 , due to the fact that the double pendulum is a continuous system and the right and left derivatives are equal to each other. Therefore, the fractional equations of motion in the case of external forcing are
, due to the fact that the double pendulum is a continuous system and the right and left derivatives are equal to each other. Therefore, the fractional equations of motion in the case of external forcing are
 (10)
(10)
It should be noticed that the right hand side of Equation (9) is zero since the  term vanishes in unforced systems. The last term on the left side of Equation (10) is the consequence of fractional-order modeling. These additional terms associated with Equations (3) and (4) are written explicitly as
term vanishes in unforced systems. The last term on the left side of Equation (10) is the consequence of fractional-order modeling. These additional terms associated with Equations (3) and (4) are written explicitly as
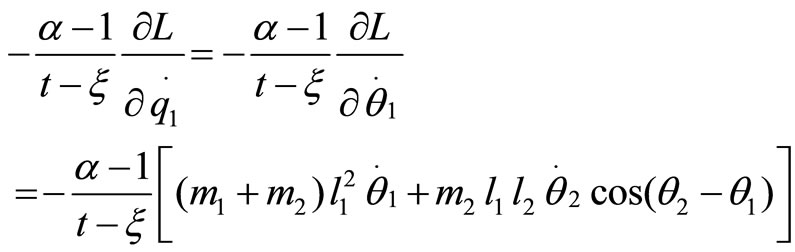 (11)
(11)
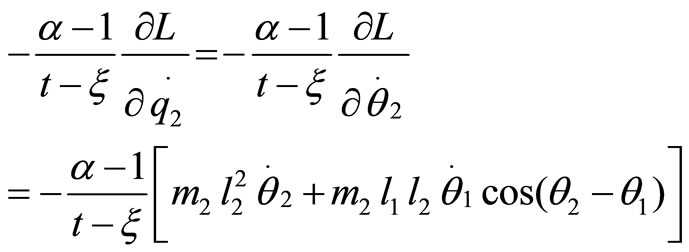 (12)
(12)
It is evident that replacing 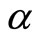 with 1 in Equation (10) yields the Lagrangian equations of motion in integer space. This is due to the fact that that replacing
with 1 in Equation (10) yields the Lagrangian equations of motion in integer space. This is due to the fact that that replacing 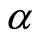 with 1 in definitions 5 and 6 yield integer-order derivatives.
with 1 in definitions 5 and 6 yield integer-order derivatives.
4. Non-Conservative Forces and Derivation of the Generalized Forces
The following five cases of non-conservative forcing conditions have been assumed in this study.
1) Horizontal forcing: A periodic force of 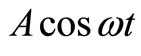 has been applied to
has been applied to  horizontally, as seen in Figure 2.
horizontally, as seen in Figure 2.
2) Vertical forcing: A periodic force of 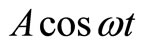 has been applied to
has been applied to  vertically, as seen in Figure 3.
vertically, as seen in Figure 3.
3) Axial forcing: A periodic force of 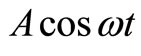 has been applied to
has been applied to 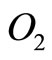 along the axis
along the axis , as seen in Figure 4.
, as seen in Figure 4.
4) Vertical forcing through the center of gravity of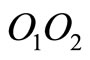 : A periodic force of
: A periodic force of 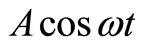 has been applied to the center of gravity of
has been applied to the center of gravity of  vertically, as seen in Figure 5. Since the arms are assumed to be homogenous, the point of application is the midpoint of
vertically, as seen in Figure 5. Since the arms are assumed to be homogenous, the point of application is the midpoint of .
.
5) General forcing: A periodic force of , making an angle
, making an angle 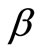 with the vertical, has been applied to
with the vertical, has been applied to , as seen in Figure 6.
, as seen in Figure 6.
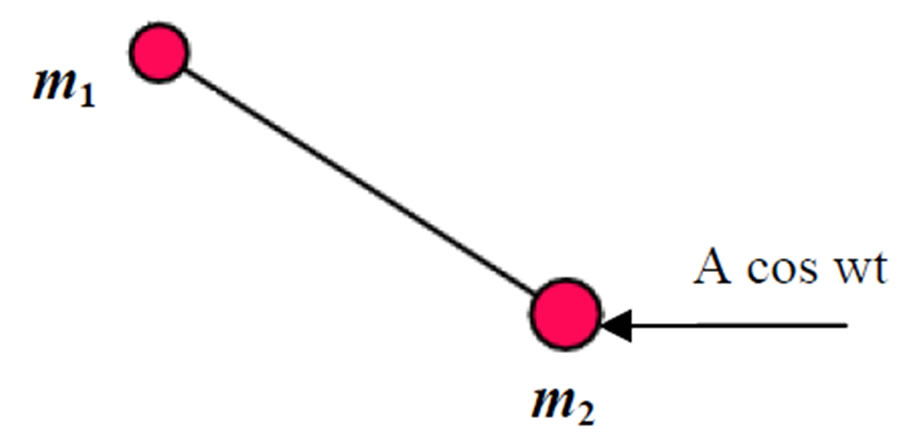
Figure 2. Case a—horizontal forcing.
Figure 3. Case b—vertical forcing.
Figure 4.Case c—axial forcing.
Figure 5. Case d—vertical forcing through the center of gravity of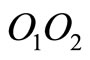 .
.
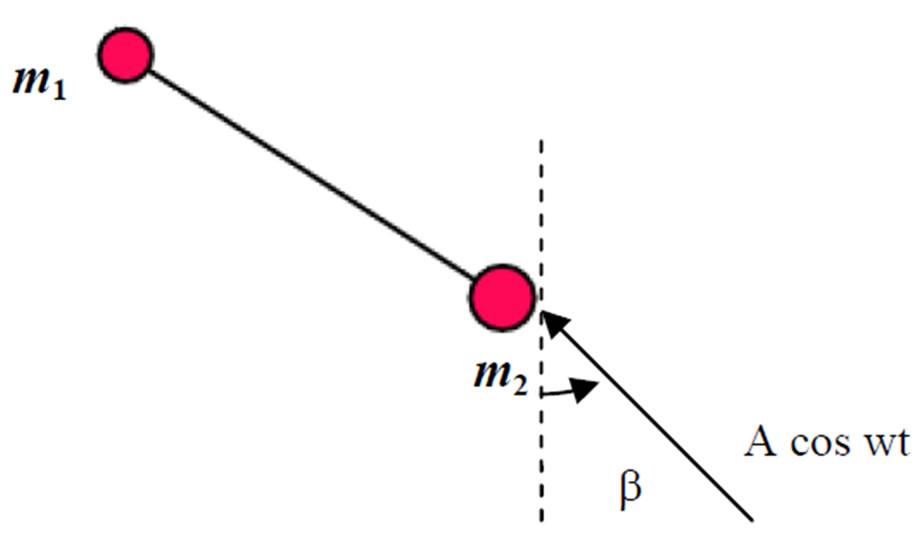
Figure 6. Case e—general forcing.
Generalized forces have been obtained using the relation
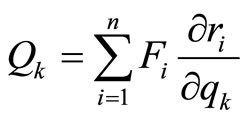 (13)
(13)
where 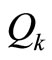 is the generalized force associated with the
is the generalized force associated with the 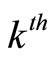 equation of motion,
equation of motion, 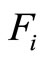 is the applied force,
is the applied force,  is the position of the point of application and
is the position of the point of application and 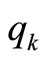 is the generalized coordinate. Apparently, no generalized forces appear in the equations of free motion and the right hand sides of Equation (10) vanish. In matrix notation, the above relation can be given as
is the generalized coordinate. Apparently, no generalized forces appear in the equations of free motion and the right hand sides of Equation (10) vanish. In matrix notation, the above relation can be given as
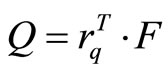 (14)
(14)
Generalized forces related to each of the forcing conditions given above were found as the following.
UCase aU Since  is the point of application,
is the point of application,
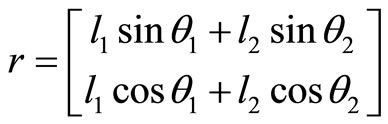

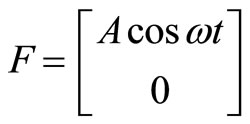

Thus, the generalized forces are
 (15)
(15)
 (16)
(16)
UCase bU Point of application is the same as in case a, and the applied force is
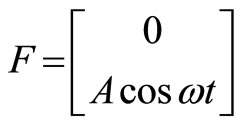
Thus, the generalized forces are
 (17)
(17)
 (18)
(18)
UCase cU Point of application is the same as in cases a and b, and the applied force is
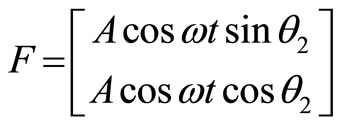
Thus, the generalized forces are
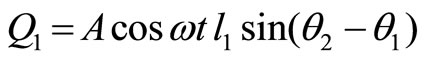 (19)
(19)
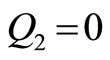 (20)
(20)
UCase dU Point of application is the midpoint of ,
,
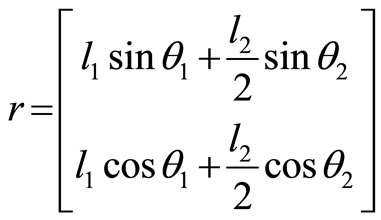
Applied force is the same as in case b. Thus, the generalized forces are
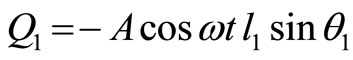 (21)
(21)
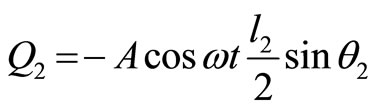 (22)
(22)
UCase eU Point of application is the same as in cases a, b and c, and the applied force is
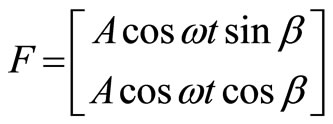
Thus, the generalized forces are
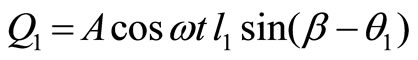 (23)
(23)
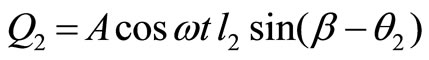 (24)
(24)
It should be observed that the generalized force terms in cases a, b and c (horizontal, vertical and axial forcing, respectively) can be derived from the generalized force term of case e. Replacing 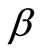 in Equations (23,24) with
in Equations (23,24) with  yields Equations (15,16); replacing
yields Equations (15,16); replacing  with 0 yields Equations (17,18); and replacing
with 0 yields Equations (17,18); and replacing 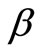 with
with 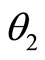 yields Equations (19,20). These are the results obtained by incorporating horizontal, vertical and axial forcing functions into the equations, respectively.
yields Equations (19,20). These are the results obtained by incorporating horizontal, vertical and axial forcing functions into the equations, respectively.
The generalized force terms 15-24 derived in this section constitute the right hand sides of the equations of motion of the forced double pendulum. 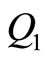 term represents the right hand side of the first equation of motion, which had been derived by differentiating the Lagrangian (2) with respect to
term represents the right hand side of the first equation of motion, which had been derived by differentiating the Lagrangian (2) with respect to  and its derivative, and likewise,
and its derivative, and likewise, 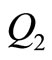 term represents the right hand side of the second equation of motion, which had been derived by differentiating the Lagrangian (2) with respect to
term represents the right hand side of the second equation of motion, which had been derived by differentiating the Lagrangian (2) with respect to 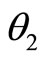 and its derivative. Apparently, both
and its derivative. Apparently, both 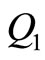 and
and 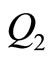 will be equal to zero when there is no forcing function.
will be equal to zero when there is no forcing function.
5. Equations of Motion
Equations describing the dynamics of the unforced double pendulum were derived in Section 2. Fractional terms related to fractional-order modeling of the system were defined in section 3. Generalized forces pertaining to each of the five forcing conditions were derived in Section 4. The complete set of equations describing the motion of the double pendulum thus become
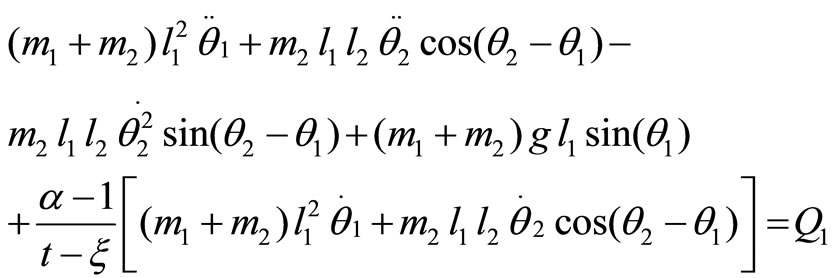 (25)
(25)
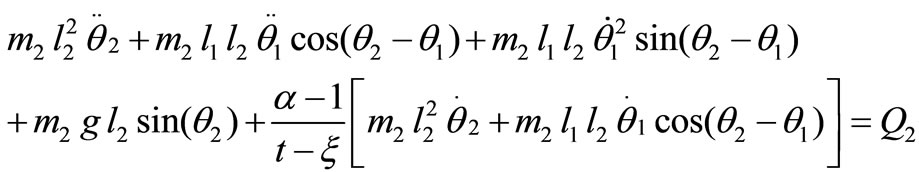 (26)
(26)
Left hand sides of the equations comprise of the terms in Equations (3,4,11,12). The terms containing 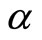 indicate the additional terms resulting from the fractional-order model, as given in Equations (11,12). Right hand sides denote the generalized force terms resulting from the forcing functions. There is a specific set of values for
indicate the additional terms resulting from the fractional-order model, as given in Equations (11,12). Right hand sides denote the generalized force terms resulting from the forcing functions. There is a specific set of values for 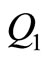 and
and  for each case of forcing, given by Equations (15-24).
for each case of forcing, given by Equations (15-24).
6. Initial Conditions and Numerical Values
In this study, three different sets of initial conditions were considered. Each equation of motion was solved for each set of these initial conditions, which are
set 1
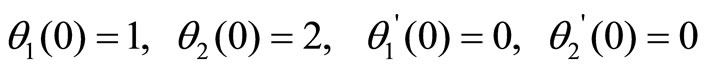
set 2
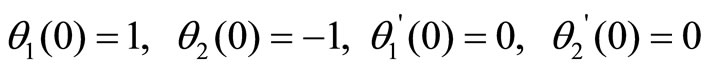
set 3
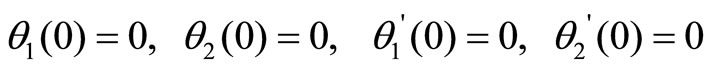
where the angles are measured in radians. Sets 1 and 2 correspond to the case where the pendulum bob has an initial displacement from equilibrium position but no initial velocity while set 3 corresponds to the case where the pendulum bob has no initial displacement and no initial velocity. It should be noticed that the last set of initial conditions yields no motion in the unforced case and cases b, c, and d. These cases are vertical forcing, axial forcing and vertical forcing through the center of gravity of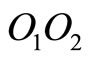 , respectively. This is because
, respectively. This is because 
 is a stable equilibrium point. Table 1 shows the cases considered in this study and the sets of boundary conditions utilized for each. Selected results will be presented in the following section.
is a stable equilibrium point. Table 1 shows the cases considered in this study and the sets of boundary conditions utilized for each. Selected results will be presented in the following section.
 ,
, 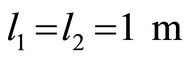 and
and 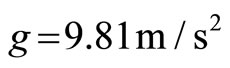 in this study.
in this study.
7. Results
A quick inspection of Table 1 reveals the cases examined in this study. The double pendulum has been modeled with and without external forcing, using both integer and fractional order modeling. It is stated above that the double pendulum cannot start its motion under null initial conditions in the unforced case and in cases of vertical forcing, axial forcing and forcing through the center of gravity of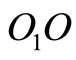 , not only when it is modeled with the integer-order approach, but also the fractional approach. Equations modeling the dynamics of all the other cases have been solved and their phase diagrams have been plotted. Blank phase diagrams were obtained for the cases where the double pendulum was not supposed to move, which verifies the calculations. The effect of the fractional variable
, not only when it is modeled with the integer-order approach, but also the fractional approach. Equations modeling the dynamics of all the other cases have been solved and their phase diagrams have been plotted. Blank phase diagrams were obtained for the cases where the double pendulum was not supposed to move, which verifies the calculations. The effect of the fractional variable  is observed. As
is observed. As  approaches 1, the results approach those obtained by integer-order modeling. This can be observed in the following figures in Table 2.
approaches 1, the results approach those obtained by integer-order modeling. This can be observed in the following figures in Table 2.

Table 1. Cases solved in this study.
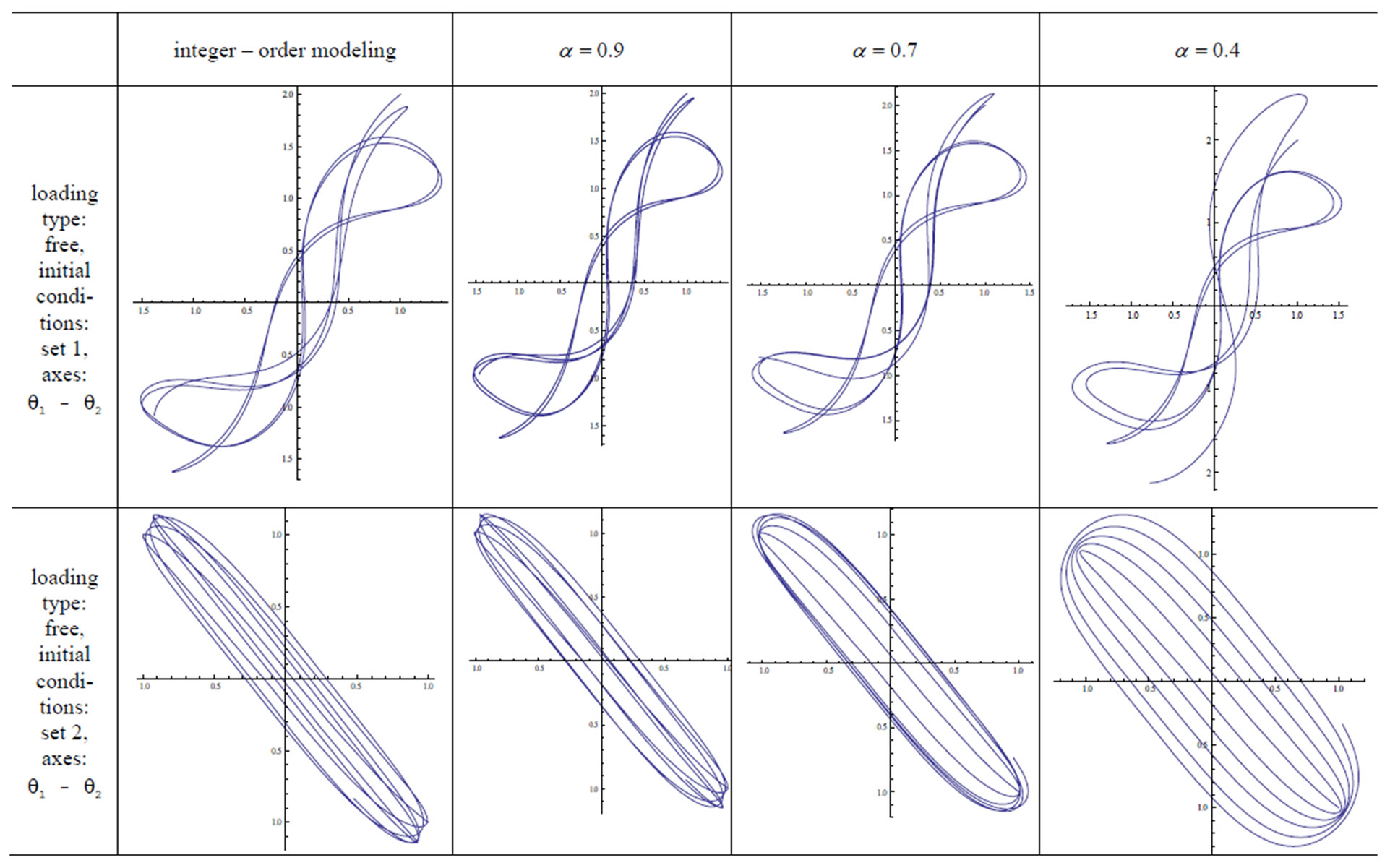
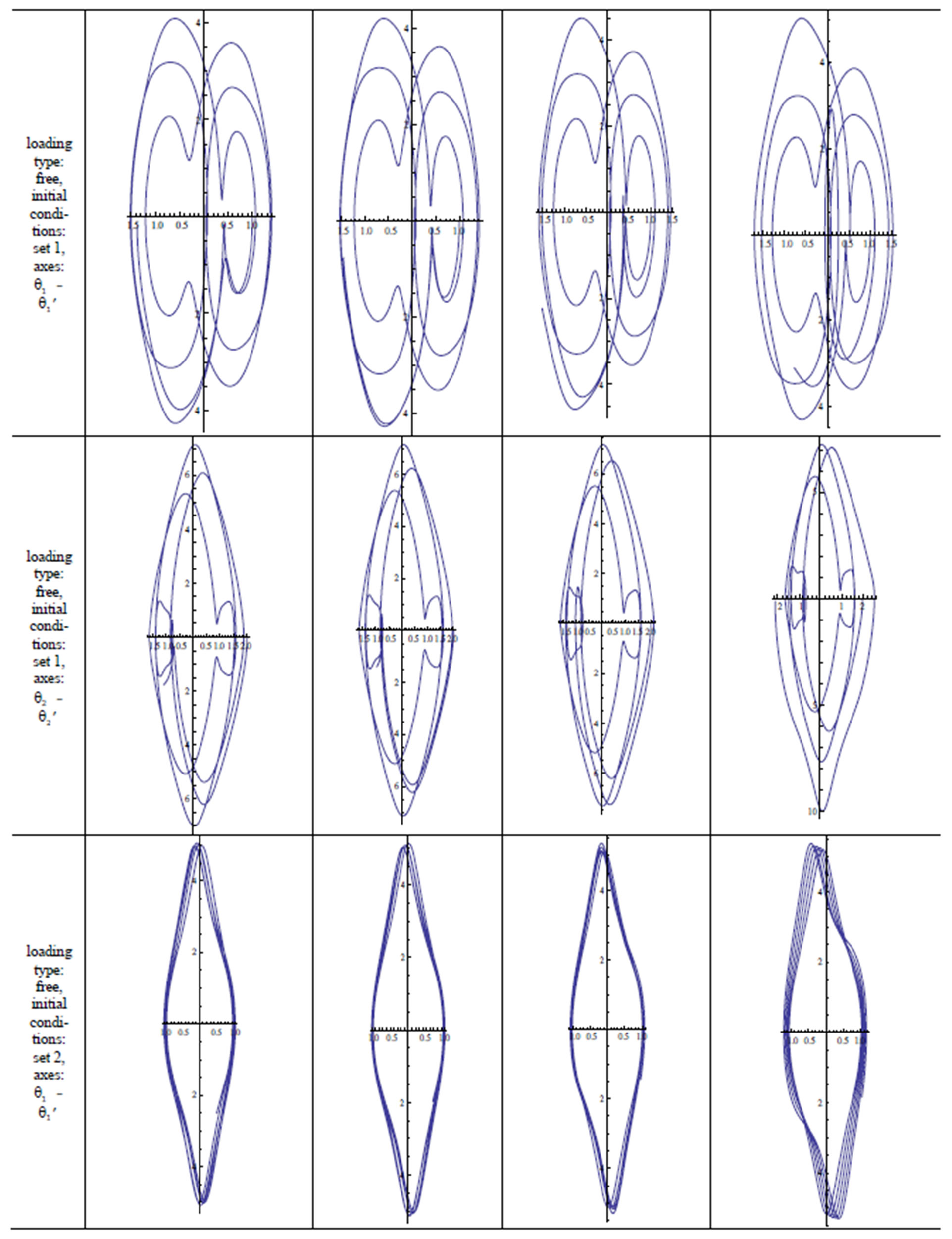

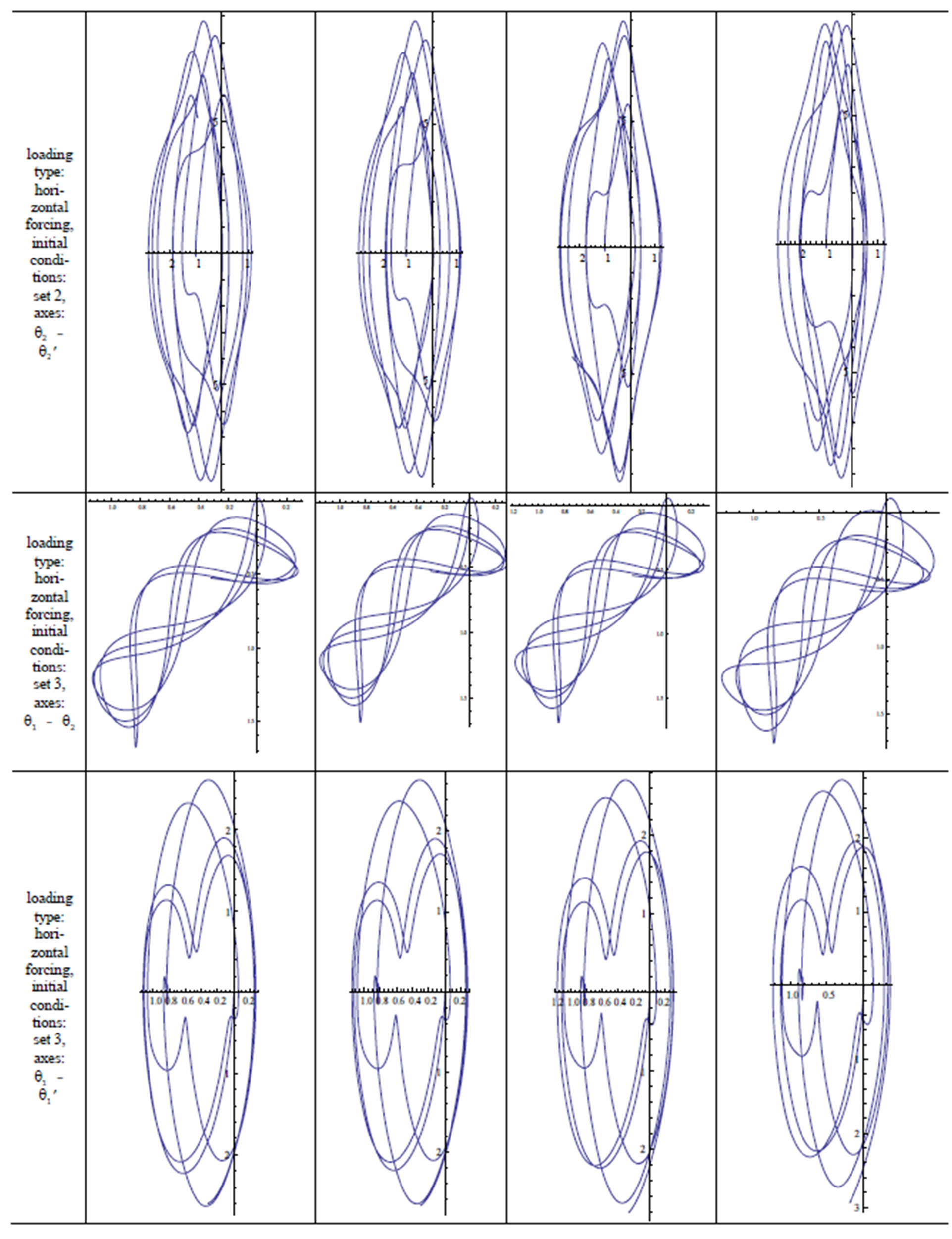
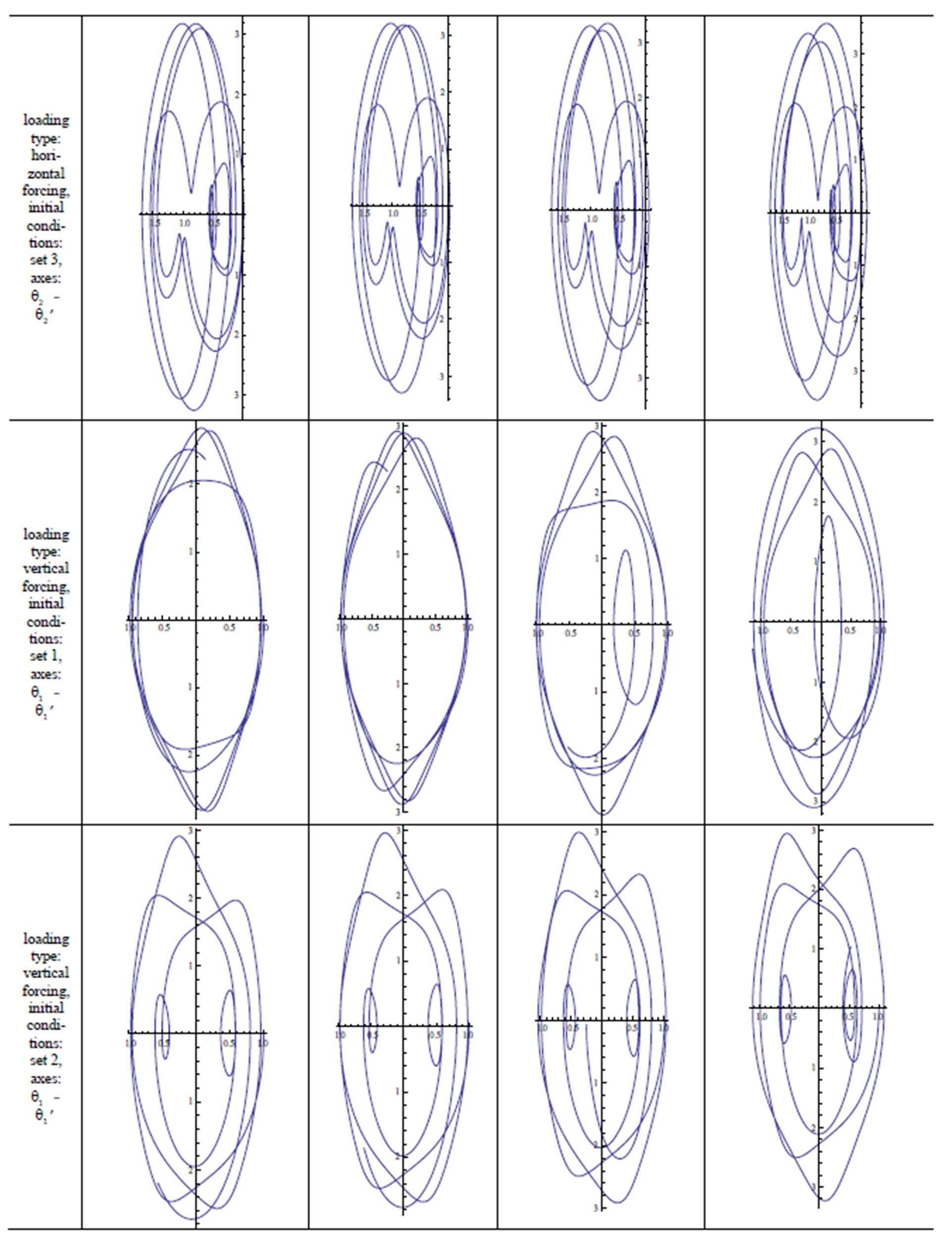
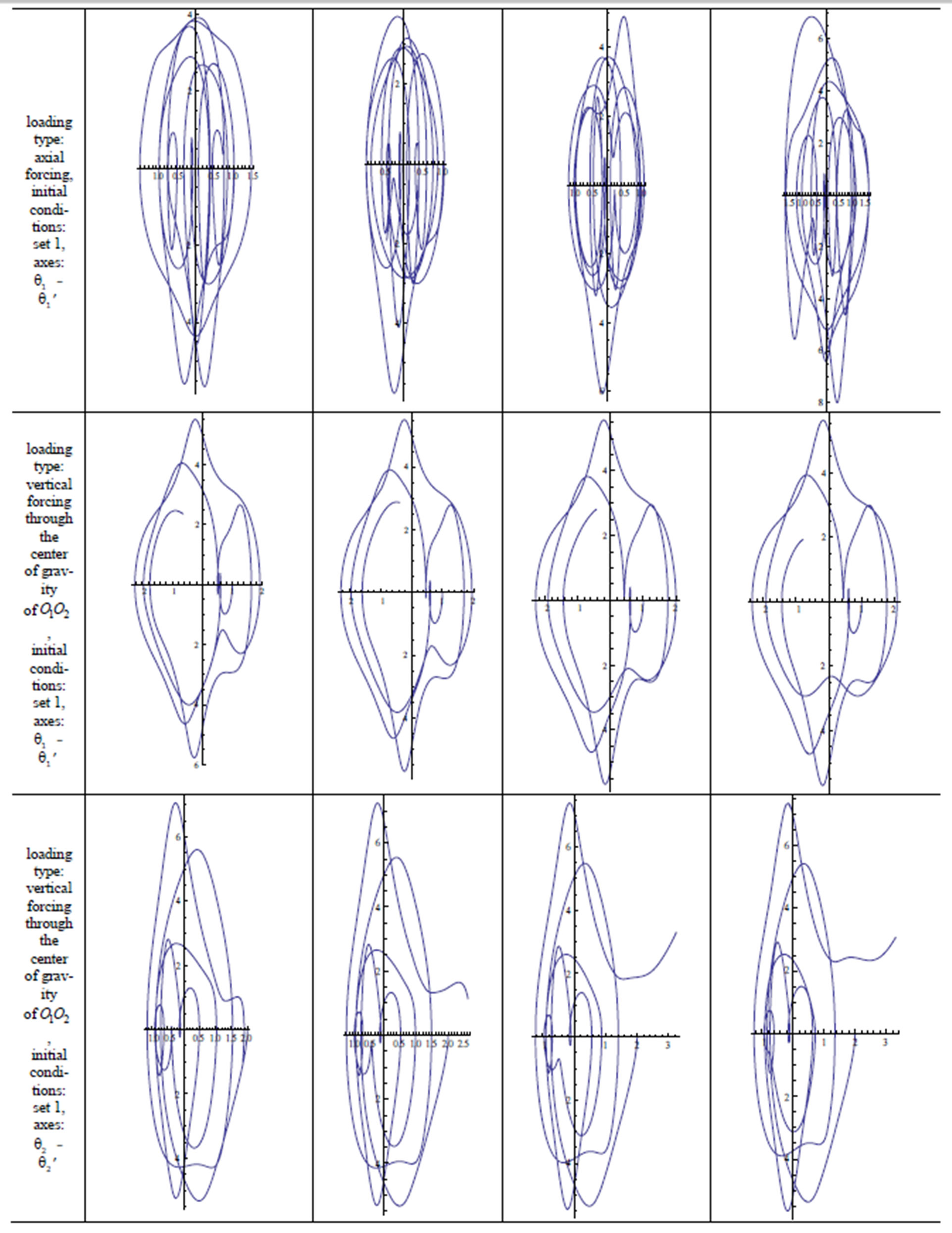
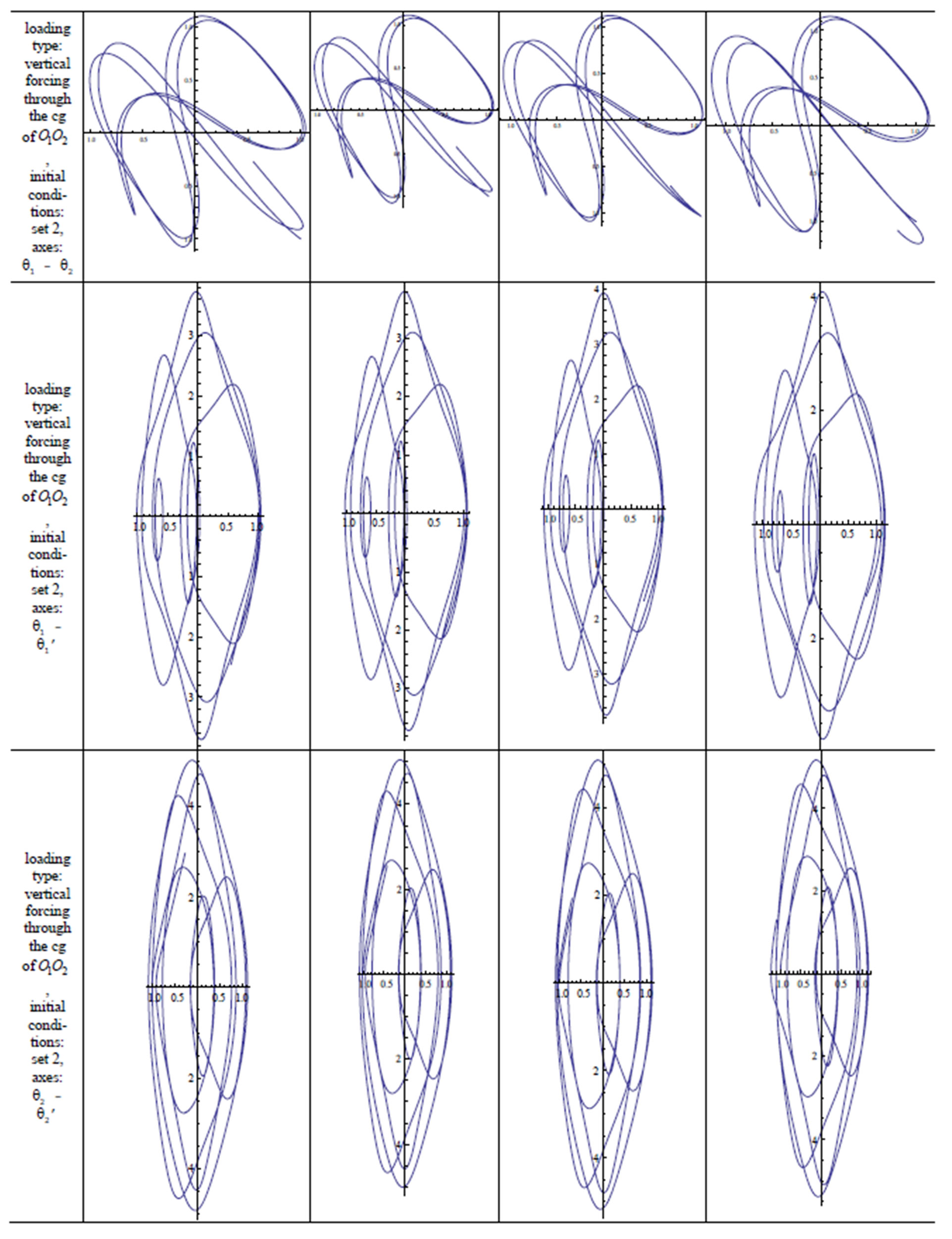

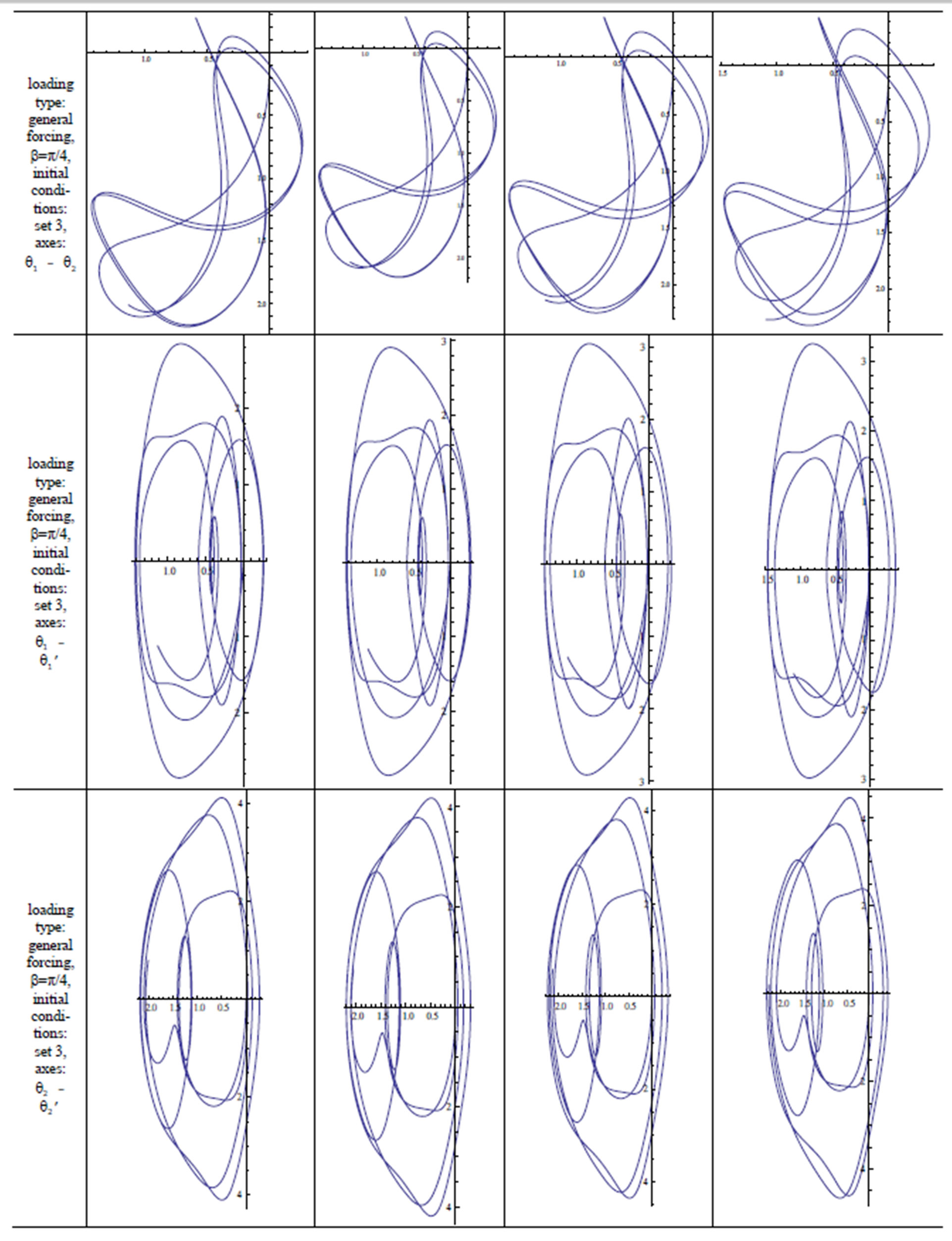
Table 2. Phase diagrams and trajectory diagrams.
In addition, this study can be used as a source for modeling pendulum-type structures in fractional space, since the governing equations are derived using a step by step procedure and the differences between integer modeling and fractional-order modeling are outlined. Physically possible initial conditions are applied in both modeling approaches and the results are presented graphically.
8. Discussion
Integer and fractional-order modeling of the double pendulum are done under various forcing conditions and three different sets of initial conditions. Three different values have been used for the fractional order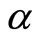 . It was observed that as
. It was observed that as 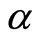 approaches 1, phase diagrams converge to those obtained by integer-order modeling. However, experiments should be conducted to obtain more realistic results about whether fractional-order models are more accurate than integer-order models.
approaches 1, phase diagrams converge to those obtained by integer-order modeling. However, experiments should be conducted to obtain more realistic results about whether fractional-order models are more accurate than integer-order models.
9. REFERENCES
- A. Ohlhoff and P. H. Richter, “Forces in the Double Pendulum, Zeitschrift für Angewandte Mathematik und Mechanik,” Journal of Applied Mathematics and Mechanics, Vol. 80, No. 8, 2000, pp. 517-534.
- A. A. Martynyuk and N. V. Nikitina, “The Theory of Motion of a Double Mathematical Pendulum,” International Applied Mechanics, Vol. 36, No. 9, 2000, pp. 1252-1258.
- U. Mackenroth, “Robust Stabilization of a Double Pendulum with an Elastic Joint and Uncertain High-Fre-
- quency Dynamics,” 16th Mediterrenean Conference on Control and Automation, France, 2008, pp. 1490-1495.
- D. Sado and K. Gajos, “Note on Chaos in Three Degree of Freedom Dynamical System with Double Pendulum,” Meccanica, Vol. 38, No. 6, 2003, pp. 719-729.
- M. P. Hanias, “Chaotic Behavior of an Electrical Analog to the Mechanical Double Pendulum,” Journal of Engineering Science and Technology Review, Vol. 1, No. 1, 2008, pp. 33-37.
- T. Stachowiak and T. Okada, “A Numerical Analysis of Chaos in the Double Pendulum,” Chaos, Solitons and Fractals, Vol. 29, No. 2, 2006, pp. 417-422.
- L. Sheu, H. Chen, J. Chen and L. Tam, “Chaotic Dynamics of the Fractionally Damped Duffing Equation,” Chaos, Solitons and Fractals, Vol. 32, No. 4, 2007, pp. 1459- 1468.
- X. Gao, J. Yu, “Chaos in the Fractional Order Periodically Forced Complex Duffing’s Oscillators,” Chaos, Solitons and Fractals, Vol. 24, No. 4, 2005, pp. 1097-1104.
- R. S. Barbosa, J. A. T. Machado, I. M. Ferreiraa and J. K. Tar, “Dynamics of the Fractional-Order Van der Pol Oscillator,” Second IEEE International Conference on Computational Cybernetics, 2004, pp. 373-378.
- M. Seredynska, “Nonlinear Differential Equations with Fractional Damping with Applications to the 1dof and 2dof Pendulum,” Acta Mechanica, Vol. 176, No. 3-4, 2005, pp. 169-183.
- S. I. Muslih and D. Baleanu, “Fractional Euler-Lagrange Equations of Motion in Fractional Space,” Journal of Vibration and Control, Vol. 13, 2007, No. 9-10, pp. 1209- 1216.
- I. Podlubny, “Fractional Differential Equati Equations,” Academic Press, San Diego, 1999.
- A. A. Kilbas, H. M. Srivastava and J. J Trujillo, “Theory and Applications of Fractional Differential Equations,” Elsevier, Amsterdam, 2006.
- L. Munteanu, T. Badea and V. Chiroiu, “Linear Equivalence Method for the Analysis of the Double Pendulum’s Motion,” Complexity International, Vol. 9, 2002, pp. 1-17.

