ABSTRACT

The connectivity of information has changed many things but not the way economists model consumers, firms and government. Information is here newly modeled as a fundamental element of microeconomic choices and utility, cost and tax functions. The results are more clearly defined metrics for losses due to cyber breaches or productivity gains from cyber investments. The integration of information into standard microeconomics also allows use of econometric and other tools to analyze the empirics of the consumer and the firm. In particular, the results identify ways in which losses in the Gordon and Loeb [1] model can be specified in more detail.

Keywords:

Microeconomics, Utility, Cost, Cyber Losses

1. Introduction

Capital and labor are the time honored categories for production inputs which are transformed into marketable goods and services. But the economy is more virtual now with information occupying a central place in economic activity. Economics has primarily dealt with information as an issue in information gathering for decision-making under uncertainty as in Bikhchandani, Hirshleifer and Riley [2] . A major area of application includes labor market signaling as in Rogerson, Shimer and Wright [3] . However, maintaining the abstraction that information is an imprecise signal for a decision or simply changes the quality or quantity of (computer) capital does not capture the many ways that information itself is an input into production. Shutting down a website and a consumer’s virtual access to a business is damaging; intellectual property and personal identity are stolen virtually, production processes can be controlled by or destroyed by changes in the information running the machines. Motivated by issues in cybersecurity, this note investigates the ways information alters fundamental structures of the consumer, firm and government. Analyzing those structures more clearly identifies microeconomic definitions of cybersecurity losses even in the absence of a decision involving uncertainty.

Gordon and Loeb [1] obtained significant insight by abstracting cyber information sets from the remainder of the economic activity of the firm or organization. Information sets were interpreted broadly; potentially including data sets, websites, accounting information, algorithms, intellectual property, electronic communications and so on. In their model and extensions as in Farrow and Szanton [4] , the effect of a cyber information breach results in a conditional loss, L, to the firm. The loss is a part of an expected value objective function where probabilities of loss are modeled separately. In Gordon, Loeb, Lucyshyn and Zhou [GLLZ, [5] ], the losses include external effects beyond the firm. There is however, value in re-integrating their sparsely defined conditional loss into the more detailed but standard microeconomic modeling of the firm, the consumer, and government. Such reintegration facilitates the decomposition of losses due to a breach, the differentiation of types of attacks, and the distinction between what GL refer to as private and external costs of an attack¹.

Microeconomics builds from an individual consumer and firm up to the market and general equilibrium levels. However, research on cyber losses to both consumers and firms has taken a more ad-hoc approach. Prior research seems to have taken two alternative approaches. One approach in the information technology literature is to develop taxonomies of types of attacks, potentially distinguished by their method of attack or the outcome as in Undercofer, et al. [8] . A second approach has focused on cost categories. Detica [9] focused on the costs associated with various stages of cyber-attacks, identifying categories of costs in anticipation, in consequence, in response, and indirect costs. Anderson, et al. [7] organize their cost analysis using direct, indirect, and defensive costs with the cost to society being the sum of these categories.

In contrast to the existing cyber focused work, the standard sequence of firm and consumer modeling is developed here in order to explicitly identify the pathways losses can occur. Such a delineation may encourage more detailed empirical modeling given the methodologies already developed for analyzing microeconomic structures. While the focus here is on the mechanism of losses due to some type of cyber activity, the dominant impact of cyber activity has been gains through many of the same mechanisms capable of generating losses.

2. Modeling Information as an Input

2.1. Information and the Consumer

Begin with the consumer who, for example, can be directly affected by breaches of Personal Identifying Information (PII) and whose choices create demand for a firm’s product.

A deterministic model identifies goods Q_i that may have characteristics dependent on embedded cyber information and capabilities, I, as is common with many consumer goods. Furthermore, transactions are facilitated by cyber information and processes typically embedded in computers, phones or other devices and linked to the internet. Consequently the good itself and its purchase is partially defined by cyber information, Q(I). Prices, P_i, are here assumed parametric in the budget constraint, Y such that:

Max Utility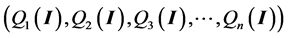

w.r.t. Q_i

Subject to: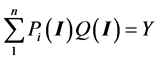

Cyber breaches can then affect the consumer’s utility through various pathways. The direct theft from a consumer, perhaps from the loss of PII, can be modeled as a discrete decline in income², Y(I). More complexly, consider that characteristics of differentiated goods are identified both by their embedded use of cyber information through software, displays, controls and so on while the transaction cost and purchase context is also influenced by cyber information. To the extent that there are changes in the cyber information embedded in the good, prices³, or income then the consumer’s demand, Q_i(I) = f(P_i(I), P_j(I), Y(I), I), changes. The total derivative of demand, Equation (1), thus identifies specific chains or pathways of effects from changes in information to observable quantities based on consumer behavior.

(1)

The consumer’s problem can also be written in terms of household production where household labor and purchased inputs yield household output as in Becker [10] or Gronau and Hammermesh [11] . For instance, loss of an individual’s time to re-establish identity or time involved with personal malware leads one to a household production model where time has a shadow price primarily measured by household labor. While not fully developing that model here, household labor can be affected, both positively and negatively, by cyber information, H(I). Other household inputs such as electricity and water are information dependent, HE(I) and HW(I), and are of concern due to potential cyber-physical infrastructure damage.

An information set (or just information) augmented consumer model thus captures: a) changes due to loss of income, b) costs associated with household production including unpaid time, c) changes in the quality of goods including the process of obtaining them, and d) potential changes in the utility function itself. For instance, the result of stolen PII from a retailer may involve changes in utility (and associated monetized value of that utility loss) reflected in a tighter budget constraint, having to spend time and other household inputs to restore their identity and changing their demand for products from that source or similar sources. In the latter case, there could be a public bad of decreased quality across multiple goods, a topic investigated in more detail below. Alternatively, the primary effect of cyber information change can be positive for the consumer (as it typically has been from non-criminal use of cyber information).

2.2. Information in the Firm and the Government

Firms are linked to consumers via the market demand (or inverse demand) function, shown above to depend on cyber information and upon aggregation across consumers. But the firm’s output also depends on its production function, f. Begin with a classical production function in which output, Q, is a function of capital and labor, f(K, L). Consideration is given first to the situation where no network or other externalities exist. The role of (ostensibly) internal cyber information, I, can be modeled as both a stand-alone input and an intermediate input embedded in and affecting the productivity of K and L. The usefulness of considering the stand-alone portion occurs for instance, when considering theft of PII or intellectual property. The capital and labor within the firm would still operate with the same productivity, but a loss occurs. Examples of an effect mediated through capital and labor is malware which can affect the productivity of both inputs. Within a firm, initially augment a production function as Q(I) = f(L(I), K(I), I). Cyber security from the firm’s perspective, absent externalities, is to consider how the production process is damaged if the I input is compromised, as from attacks which may affect confidentiality, integrity, authenticity, availability to users and so on. Further, I may affect the very definition of the output such that differentiated products may viewed by the consumer differently if they are secure or not.

Now consider the role of public goods (or bads) which is the mechanism through which externalities occur. Current production typically depends not only on the firm’s own cyber information input, I, but also that of the external cyber system to which it is connected, I, comprised at least of all the linkages the firm uses on the internet or more indirect effects as through communications, control of utilities, and so on. Such a public good input may affect production directly or indirectly through other inputs. For instance, infrastructure damage to I may both impair the firm’s internal cyber information input as well as capital. Further, an attack over the internet may result in technological adaptation or response by the firm. While this could be considered an entirely new production function, here such responsive actions are modeled as direct shifts in output or shifts mediated through capital and labor with resulting implications for costs. A production function including both types of internal and external cyber information can then be written as Q(I, I) = f(L(I, I), K(I, I), I(I), I). There is also the standard cost function―representing the minimum cost of producing a level of output given the production function and input prices―here shortened to focus on the role of information as C(I, I).

The final element affected by cyber information is demand for the firm’s product which, in perfect competition, is pre-determined at the firm level but jointly determined by supply and demand at the market level. At the market level, the internal cyber information is presumably so small as to not affect the price, but an external impact of cyber information may exist at the market level. Hence a competitive market price depends on external cyber information P(I). For an imperfectly competitive firm the price is a function of the firm’s marginal revenue and marginal cost and, given the prominent role of internet sales and communication, hence characterized as a function of both the internal and external cyber information, P(I, I).

Consequently the pre-tax profit function for a firm can be written as π(I, I) = P(I, I) Q(I, I) − C(Q(I, I)) with some of the internal cyber information possibly irrelevant to a competitive firm. However, government and industry also interact in a variety of ways. The production function itself may be constrained by various regulatory policies. Changes in such policies can result in a changed production function perhaps but not necessarily related to cyber information. More directly, a number of taxes transfer money from industry (and the consumer) to Government. The bi-directional impact of cyber information on taxes and tax revenue is here modeled by a tax on profits, τ(π(I, I)), although the focus below will be on the effect of the external effects. Including the tax effect allows for losses in government revenue potentially due to loss of intellectual property, or gains if government imposes taxes or fines on a firm due to cyber information breaches and or other actions.

Define the total potential private supply side loss due to information as the total derivative of the profit function:

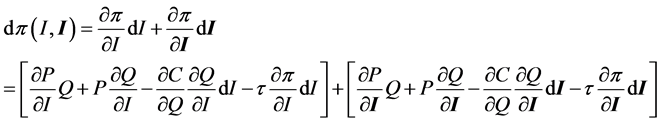(2)

Each term in Equation (2) represents a pathway through which changes in information can affect profit where the key pathways are through price, quantity, cost, and taxes. One may also ask, what about financial dimensions of firms such as stock market prices, net worth, and borrowing costs? These financial dimensions are considered here as derivative of the profit position of the firm. If profit expectations decline due to cyber breaches, that decline is expected to affect the financial condition of the firm including its forecast net worth, stock value and so on. Such links could be analyzed through the impact on the profit function as in Campbell et al. [12] .

Finally, Government is potentially affected by cyber information both through its own production and through its financing from taxes on firms and consumers. Regarding government production, the same pathways occur as with private firms with the caveat that neither costs are assumed to be minimized nor is social profit maximized. Hence government output is affected by both its internal and external cyber information, G(I,I) through the processes similar to those above.

3. Defining Losses

3.1. Deterministic Losses

The literature on cyber costs uses various loss categories such as direct, indirect, defensive and so on. Such categories may be informative for particular data sets but are not economically well defined terms. Table 1 presents several candidate classifications based on widely used language from accounting, microeconomics and macroeconomics.

The accounting terms “direct” and “indirect” have little classification power as cyber information losses (or gains) are spread across both production and “back office” processes which is central to the accounting definition. The distinction between private, external, and pecuniary effects from microeconomics has some classification power, although cyber losses are almost always initiated through an externality; they are not the result of a voluntary exchange. Like the spread of disease however, there can be an initial loss which is spread as an additional externality, as through malware. Pecuniary externalities can exist as markets are affected. Finally, macroeconomic terms have some classification power by incorporating the production and market linkages across industries. For instance, the banking sector may incur losses from re-issuing cards as the result of a PII data breach in another industry. In short, the macroeconomics reminds us of industry interactions such as when an information loss in industry j causes a change in industry i. That change may operate through the price mechanism, the legal system or other mechanisms. Similarly, interactions may occur through the endogeneity of the household sector as with induced effects. Finally, there may be political economic effects through government, including regulation.

The modeling of Section 2 allows loss definitions to depend on the partial derivatives that are affected. Consequently, direct effects are here taken to be the partial derivatives in the consumer, firm, and government problems that are not mediated through market prices or through non-market responses such as regulation. Secondary (or indirect including induced) effects are those responses mediated through the market. The direct effects

identified above are then the partial derivatives: 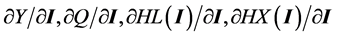for the consumer and 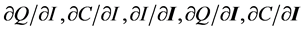for the firm, noting that (associated with taxation) is affected by both direct and indirect changes to be further defined below. These direct effects are identified by the economic actor and the mechanism of impact rather than whether the actor chooses, for instance, to alter their production function via changes in software, capital, labor or some other aspect. Consequently, in the case of PII, both damages incurred by a consumer and monitoring or re-issue costs in the financial sector would be deemed direct, while possible changes in interest rates charged would be indirect as that latter is mediated through the market mechanism.

The secondary or indirect effects are then reflecting the interactions through the marketplace or regulation.

Illustrative components of loss from two types of cyber breaches, payment card fraud and intellectual property, are presented in Figure 1 for direct costs and Figure 2 for indirect costs. The type of cyber breach is identified on the left with arrows leading to categories of effects―the partial derivatives―and a partial linkage to categories identified in Anderson, et al. [7] .

This enumeration of core pathways for cost in standard economic terms has the potential to identify costs typically ignored, such as potentially positive or negative price effects, and to provide a structure in which to identify other pathways and elements of loss. Economists are familiar with estimating elements of consumer demand and firm costs and production. The proposed framing of losses into a standard economic framework may facilitate the transition of empirical methodologies to cyber loss estimation and estimation of the partial derivatives based on data.

3.2. Some Effects of Uncertainty in Defining Losses

The loss estimates in Gordon and Loeb [1] and Gordon, Loeb, Lucyshyn and Zhou [5] are part of the objective function where the expected net benefit of a cyber investment is maximized. The losses, elaborated upon above, are the conditional losses where cyber security investment expenditures affect the probability of a successful attack. Continuing to focus on losses, the model of the consumer and firm has long been extended to conditions with uncertainty based on the expected utility model and more recently, non-expected utility models.

A natural extension to expected value optimization is expected utility maximization. To the extent that losses are potentially large so that a significant gamble is involved, then some risk aversion may be present as in Eeckhoudt, Gollier and Schlesinger [13] . Numerous methods exist in economics and decision analysis to elicit utility functions subject however, to the more restrictive assumptions that imply cardinal instead of ordinal utility (e.g. [14] [15] ). The concern by some firms for a reputational effect from a cyber breach or intellectual property theft may well warrant extending the model of losses to expected utility instead of expected value. Consideration of risk aversion leads naturally to consideration of insurance as a risk management strategy in addition to prevention which has indeed occurred.

However, the descriptive validity of the expected utility model is being questioned by behavioral economists and psychologists with a rich and rapidly evolving literature on consumer and firm behavior under uncertainty (Della Vigna, [16] ). That literature identifies a number of outcome anomalies such as the importance of reference points and asymmetric treatment of gains and losses as well as more complex treatment of probability than in the expected utility model. An analyst seeking a descriptive model of cyber losses may wish to include consideration of such factors. In empirical practice, such consideration can simply involve a different specification of an assumed utility function as compared in Farrow and Scott [17] .

Although this note has focused on defining conditional losses, cyber investments are often modeled as directly affecting the probability of the loss. Given that framework, the dynamic aspect of cyber security―new weakness are constantly being found and defenses are evolving―may best be incorporated into the probability function rather than making production functions dynamic although the latter remains a possibility. Similarly, behavioral models of probability as with cumulative prospect theory may be descriptively appropriate to consider as synthesized by Waaker [18] .

4. Conclusion

Previous categories of costs from cyber improvements and losses have conformed to general professional categories but have not been specific about the pathways through which gains and losses can occur. This paper brings information, both internal and external, into the canonical structure of microeconomic models of the consumer, the firm, and government. Impacts are then identified through the full set of partial derivatives for utility, price, quantity, profit, and taxes. The increased definitional detail facilitates the use of statistical tools to study the behavior of consumers and the firm.

Acknowledgements

Appreciation is extended to Anupam Joshi, Matt Shabat and Jules Szanton for comments and discussion. Funding was provided by the Department of Homeland Security National Center on the Risk and Economic Analysis of Terrorism Events (CREATE).

Cite this paper

Farrow, S. (2016) Cybersecurity: Integrating Information into the Microeconomics of the Consumer and the Firm. Journal of Information Security, 7, 281-290. http://dx.doi.org/10.4236/jis.2016.75023

References