Circuits and Systems
Vol.05 No.08(2014), Article ID:48609,10 pages
10.4236/cs.2014.58020
CMOS Phase and Quadrature Pulsed Differential Oscillators Coupled through Microstrip Delay-Lines
Francesco Stilgenbauer, Stefano Perticaroli, Fabrizio Palma
Department of Information Engineering, Electronics and Telecommunications, “Sapienza - University of Rome”, Rome, Italy
Email: francesco.stilgenbauer@gmail.com, perticaroli@die.uniroma1.it, palma@die.uniroma1.it
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 May 2014; revised 3 July 2014; accepted 11 July 2014
ABSTRACT
An innovative solution to design phase and quadrature pulsed coupled oscillators systems through electromagnetic waveguides is described in this paper. Each oscillator is constituted by an LC differential resonator refilled through a couple of current pulse generator circuits. The phase and quadrature coupling between the two differential oscillators is achieved using delayed replicas of generated fundamentals from a resonator as driving signal of pulse generator injecting in the other resonator. The delayed replicas are obtained by microstrip-based delay-lines. A 2.4 - 2.5 GHz VCO has been implemented in a 150 nm RF CMOS process. Simulations showed at 1 MHz offset a phase noise of −139.9 dBc/Hz and a FOM of −189.1 dB.
Keywords:
Voltage Controlled Oscillator, Microstrip, Delay-Line, Phase and Quadrature, Phase Noise

1. Introduction
Pushed from the ever-increasing demand in the electronic devices market for personal mobile devices and for wireless sensor networks, the research on innovative techniques for lowering energy requirements and costs of the electronic hardware is an extensively treated subject. At the core of every of above mentioned device, certainly an RF-IC resides, since it accomplish the necessary functional block for the establishment of a RF communication. In particular, the upconversion/downconversion task in RF-ICs usually represents the subsystems involving the major wafer area and power consumption. Toward the reduction of both areas occupation and power are placed CMOS Pulsed Bias Oscillators (PBOs). The PBO approach represents a technique exploiting the time-varying properties of electronic oscillators system. This technique can be applied to oscillators constituted of harmonic resonators refilled by active devices acting as current generators. This oscillator class aims to reach high performance in terms of phase noise with reduced energy requirements with respect to their non-pulsed counterparts. Basing on the results of Floquet Theory applied to a single oscillator [1] , we extended the pulsed bias concept to a coupled phase and quadrature system in [2] . We proved that the pulsed bias approach allows to minimize noise injection onto the Floquet Eigenvector with unitary eigenvalue, leading to decrease phase noise of generated fundamental in particular at low frequency offsets [3] [4] . However, in the effective implementation of pulsed bias architectures, the introduction of a delay is necessary for proper positioning of refilling current pulses. In the most common way, a delay can be obtained with the charging of a capacitor through a dissipative media [5] . Unfortunately, using an RC-based delay is not possible to set the pulse width independently from the pulse position. This issue is explained considering that, in the cascading of lumped elements circuits, the total delay time strictly depends on the number of stages and how they are connected. In this paper we propose a circuital solution based on the joint use of decoupling stages from resonator and of microstrip delay-lines capable to break such constraint and, at the same time, to establish coupling among oscillators with a desired phase relation. The paper is organized as follows. In Section 2 the proposed architecture is introduced, focusing on the explanation of the concept for the coupling between two oscillators in phase and quadrature. In Section 3 the theoretical analysis of the delay-line is pursued and insights for proper design are derived. In Section 4 the implementation on RF CMOS process is reported and simulation comparison with a non-pulsed architecture built in the same technology is discussed as well as a comparison with literature is given.
2. Proposed Architecture
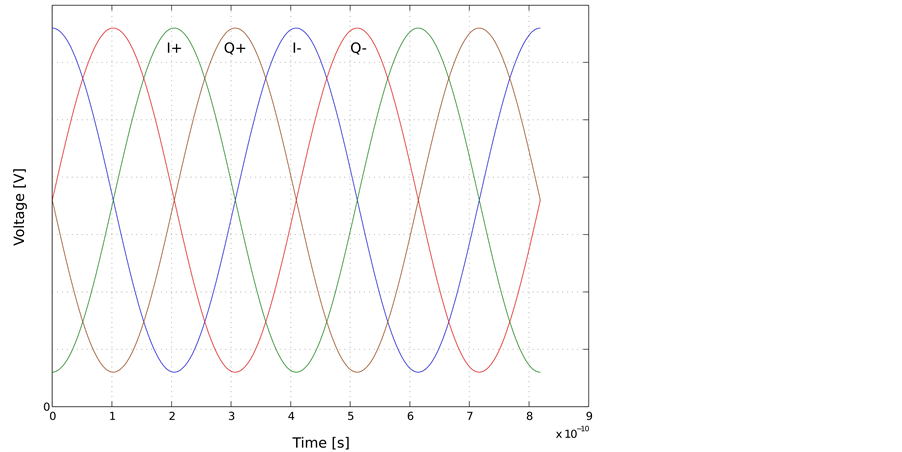
The outputs of a phase and quadrature oscillator are phase shifted replicas of a fundamental frequency 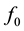 as drawn in Figure 1.
as drawn in Figure 1.
The voltage maximum of a delayed sinusoid from a resonator can be hence used to generate refilling pulses, synchronized at output voltage minimum of another resonator. Thus in this paper, we propose to couple two oscillators applying a fixed delay of 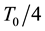 where
where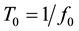 . In particular we choose to realize the delay by a microstrip transmission-line.
. In particular we choose to realize the delay by a microstrip transmission-line.
In a lossless transmission-line the secondary constants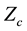 , characteristic line impedance, and
, characteristic line impedance, and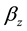 , propagation constant, are both real number. The voltage of the transmission-line equation as a function of the
, propagation constant, are both real number. The voltage of the transmission-line equation as a function of the  is given by
is given by
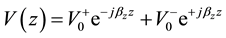 . If the load is matched to the
. If the load is matched to the , the contribution of the regressive term
, the contribution of the regressive term 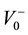 is neg-
is neg-
ligible and the transfer function between the input port, at , and the output port,
, and the output port, 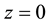 , of the transmission-line results in
, of the transmission-line results in
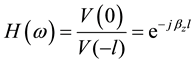 (1)
(1)
where  is the total line length.
is the total line length.
If 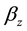 has linear increase with frequency, the transmission-line behaves as a delay-line. The delay
has linear increase with frequency, the transmission-line behaves as a delay-line. The delay 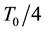 is related to the
is related to the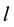 , through
, through

where 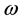
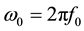
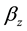
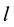
tablished considering the condition 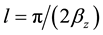
in a phase and quadrature PBO (PQPBO) are needed.
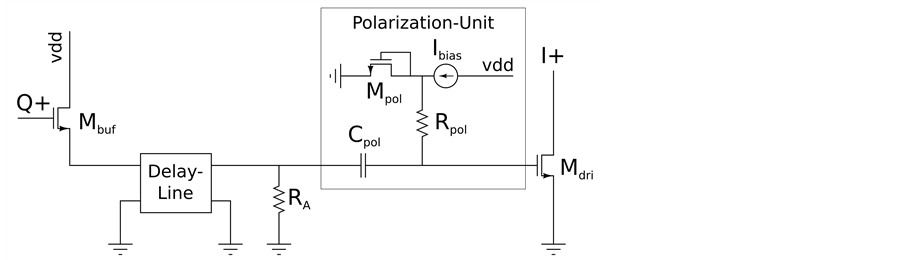
The reference schematic of the oscillator is presented in Figure 2. The system is formed by four coupled LC tanks, subdivided in two blocks, 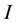
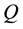
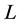

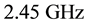
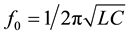
The losses are compensated by the introduction of the current pulse generators (PG) as showed in Figure 2. The PG circuit is reported in Figure 3.
Figure 1. Typical output signals of a phase and quadrature oscillator.
Figure 2. Oscillator schematic of the proposed PQPBO.
Figure 3. Pulse generator schematic.
The following description refers to the PG recharging the 

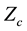
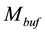
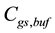
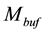
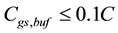
This bound grants an effective isolation of the resonator from the loading effect of PG input. Then, a triple- well is used to connect the 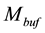
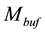
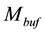
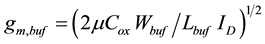
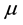
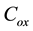
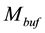
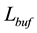
transistor width and length, respectively. If 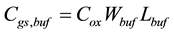
glecting the dependence on transistor operating region), we can derive an upper bound for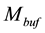
scending from Equation (3) it implies 

This bound must be accounted because an eventual low 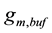
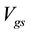
To this aim, the DL is introduced to obtain the delay necessary to synchronize the refilling instant. The values of 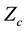
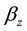
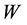
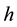
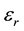
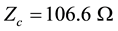
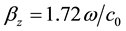
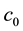
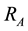
The Polarization-Unit (PU), formed by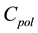


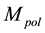
the driver transistor gate 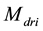
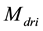
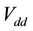

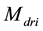
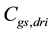
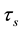
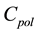
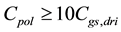
and, descending from this choice, the derivation of the equivalent resistance, 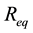
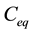
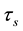
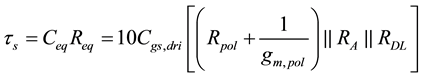
where 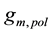
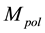
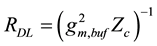
ter-wave DL transformer loaded by the source follower. In 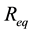
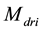
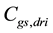
rapid exponential decay than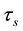
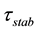
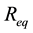
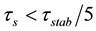
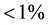
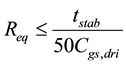
We notice in 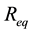
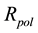
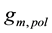
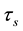
Finally, the 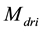
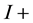
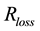
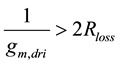
It worth noticing the 
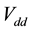
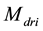
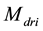
Follows the DL matching description. In first approximation, DL is described with its secondary constants 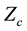
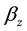
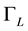

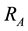
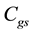
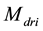


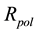
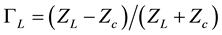
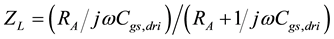
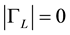
imposed because of the resistive matching, but the value of 
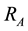
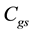
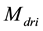
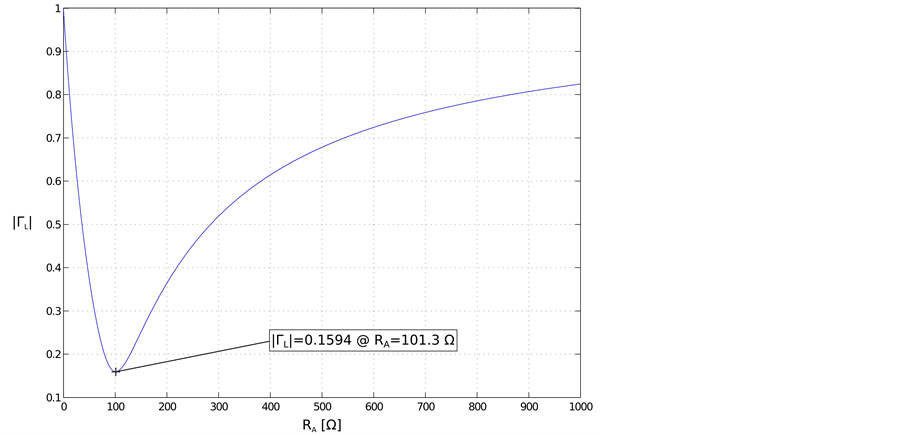
In Figure 4 the reflection coefficient as a function of 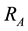


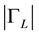

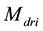
The delay-line is characterized by the transfer function on the 
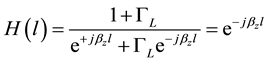
that takes into account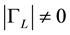
condition 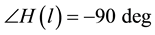
3. Delay-Line implementation
The DL unit is implemented through a waveguide structure such a microstrip. As a first microstrip design step, literature formulas [6] [7] can be used to obtain the desired 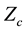
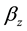
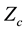
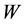
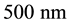
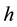
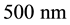
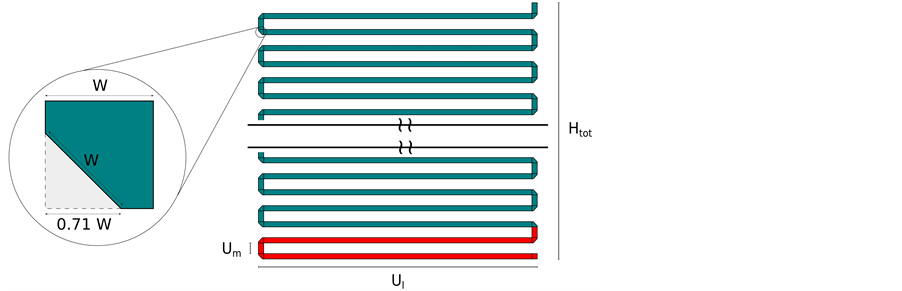
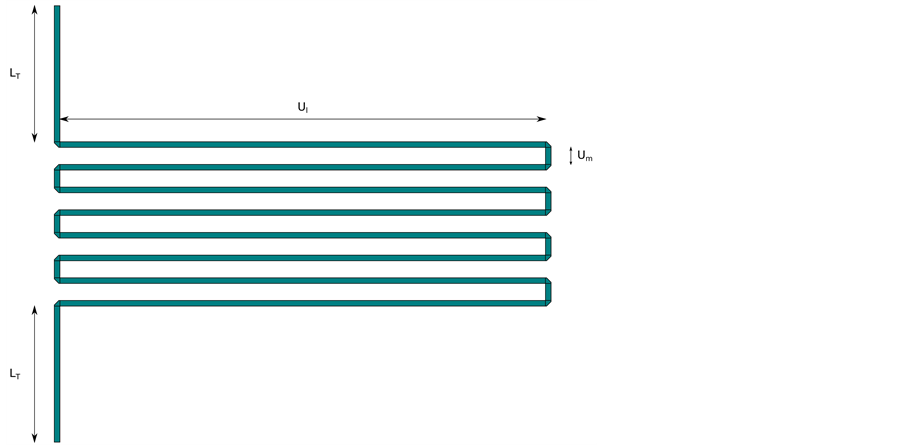
In Figure 5 a detail of the microstrip layout is reported. In black the basic module of the meander is highlighted in red. In detail of layout 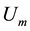
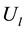

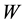
Figure 4. Reflection coefficient as a function of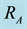
Figure 5. Detail of layout of the proposed folded microstrip delay-line.
The distance 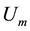
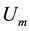
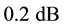
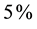
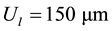
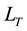
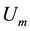
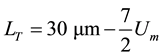
If the condition in Equation (10) is not respected, the scattering parameters variation also depends on the 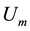
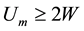
The microstrip reported in Figure 5 has been sized in order to obtain the 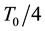

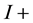
Figure 6. Simplified folded microstrip delay-line.
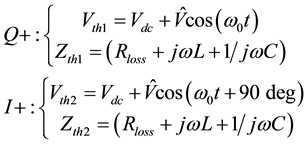
The value of 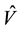
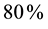
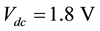
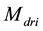
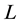
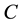
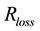
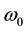
The length of the microstrip is initially chosen by Equation (9). Progressive adjustments of the 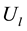
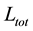
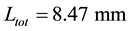
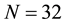
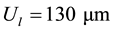
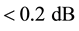
4. Simulation results and Literature Comparison
The oscillator has been implemented in the LFoundry 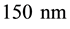
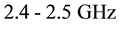

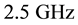
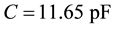
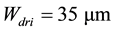
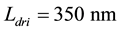
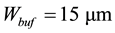
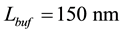
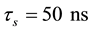


In architecture proposed in [9] the coupling between the two oscillators is reached by the introduction of coupling transistors in parallel to the crossed pair transistors. The crossed pair transistors of reference quadrature VCO, indicated with
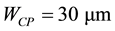
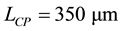

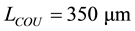
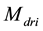
In the first comparison the oscillation amplitudes are kept at a fixed level of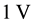

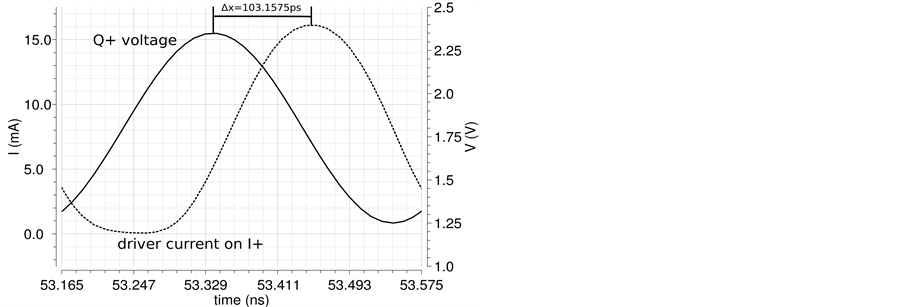
In Figure 7 the transient PSS node voltages of 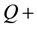
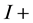
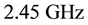
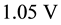
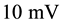
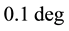
In Figure 8 the transient PSS results of the phase relation between the 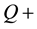
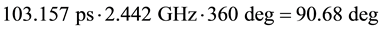

lation is not directly related to the overall quadrature phase error between the tank node voltages signals, since the receiving resonant tank undergoes to a pulling due to the whole current pulse rather than to the position of the peak only. This phenomenon results in an attenuation of the quadrature error of about an order of magnitude in phase degree, allowing the phase error between voltage signals to be lower than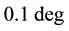
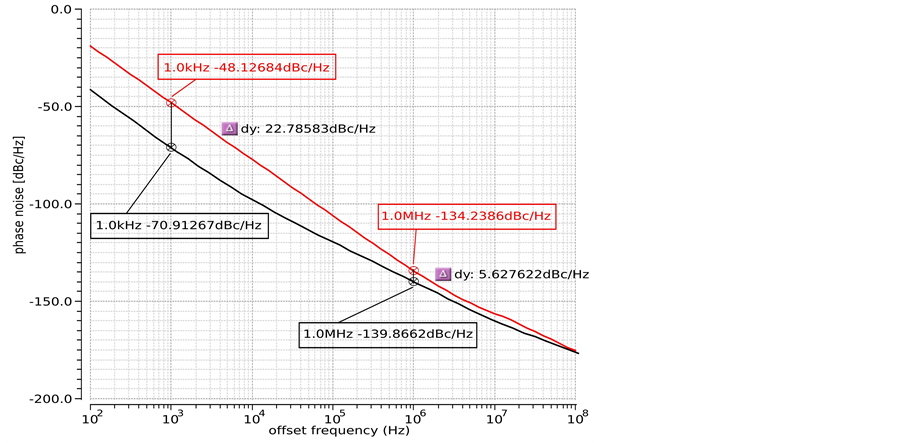
The phase noise results are presented in Figure 9 for VCOs running at 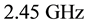
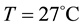
As expected from a pulsed bias architecture the phase noise improvement is consistent especially at low offsets. However, to avoid bias dependence on results, we set the comparison at 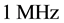
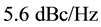
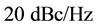
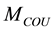
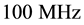
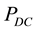
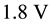
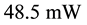
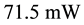
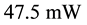

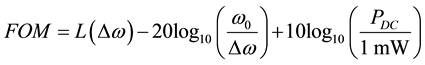
According to Figure of Merit in Equation (12), phase noise 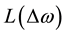
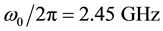
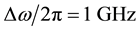



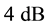
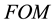
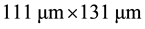

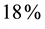
In the second comparison we gather a list of recently proposed phase and quadrature VCO architectures with both coupling based on active devices and on passive components. The results are reported in Table 1, showing that the proposed PQPBO may reach a state-of-the-art 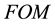
5. Concluding Remarks
In this paper a PQPBO based on a novel coupling method has been proposed. The coupling method adopts a delay-line implementation with an extremely compact meander microstrip structure. The design equations for the PQPBO, with a dedicated section on the DL optimization, have been pursued. The PQPBO has been implemented
Figure 7. PSS transient result of 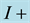
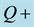
Figure 8. PSS transient result of 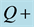

Figure 9. Phase noise results for the PQPBO (black trace) and for the refe- rence oscillator (red trace).
Table 1. Comparison with literature phase and quadrature VCOs.
at LVS level in a LFoundry 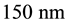
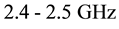
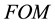
Cite this paper
FrancescoStilgenbauer,StefanoPerticaroli,FabrizioPalma, (2014) CMOS Phase and Quadrature Pulsed Differential Oscillators Coupled through Microstrip Delay-Lines. Circuits and Systems,05,181-190. doi: 10.4236/cs.2014.58020
References
- 1. Perticaroli, S., Luli, N. and Palma, F. (2011) Derivation of Floquet Eigenvectors Displacement for Optimal Design of LC Tank Pulsed Bias Oscillators. SCIRP Circuits and Systems, 2, 311-319.
http://dx.doi.org/10.4236/cs.2011.24043 - 2. Perticaroli, S., Palma, F. and Carbone, A. (2011) Phase and Quadrature Pulsed Bias LC-CMOS VCO. SCIRP Circuits and Systems, 2, 18-24.
http://dx.doi.org/10.4236/cs.2011.21004 - 3. Traversa, F.L. and Bonani, F. (2011) Oscillator Noise: A Nonlinear Perturbative Theory Including Orbital Fluctuations and Phase-Orbital Correlation. IEEE Transactions on Circuits and Systems I, 58, 311-319.
- 4. Carbone, A. and Palma, F. (2006) Considering Orbital Deviations on the Evaluation of Power Density Spectrum of Oscillators. IEEE Transactions on Circuits and Systems-II: Express Briefs, 53, 438-442.
- 5. Bizzarri, F., Brambilla, A., Perticaroli, S. and Gajani, G.S. (2011) Noise in a Phase-Quadrature Pulsed Energy Restore Oscillator. European Conference on Circuit Theory and Design (ECCTD), 465-468.
- 6. Bahl, I.J. (2003) Lumped Elements for RF and Microwave Circuits. Artech House, Norwood.
- 7. Gupta, K.C., Garg, R. and Bahl, I.J. (1996) Microstrip Lines and Slotlines. 2nd Edition, Artech House Inc., Norwood.
- 8. Douville, R.J.P. and James, D.S. (1978) Experimental Study of Symmetric Microstrip Bends and Their Compensation. IEEE Transactions on Microwave Theory and Techniques, 26, 175-182.
http://dx.doi.org/10.1109/TMTT.1978.1129340 - 9. Peng, K.C. and Lee, C.H. (2012) A 5 GHz CMOS Quadrature VCO with Precise Quadrature Phase. Microwave Conference Proceedings (APMC), Asia-Pacific, 1211-1213.
- 10. Torkzadeh, P., Atarodi, M. and Javidan, J. (2009) A Low Power, Low Phase Noise, Square Wave LC Quadrature VCO for ISM Band. Circuits and Systems and TAISA Conference, Toulose, 1-4.
- 11. Gierkink, S.L.J., Levantino, S., Frye, R.C., Samori, C. and Boccuzzi, V. (2003) A Low-Phase-Noise 5-GHz CMOS Quadrature VCO Using Superharmonic Coupling. IEEE Journal of Solid-State Circuits, 38, 1148-1154.
http://dx.doi.org/10.1109/JSSC.2003.813297 - 12. Huang, T.H. and Tseng, Y.R. (2008) A 1 V 2.2 mW 7 GHz CMOS Quadrature VCO Using Current-Reuse and Cross-Coupled Transformer-Feedback Technology. IEEE Microwave and Wireless Components Letters, 18, 698-700.
http://dx.doi.org/10.1109/LMWC.2008.2003477 - 13. Huang, G. and Kim, B.S. (2009) Low Phase Noise Self-Switched Biasing CMOS LC Quadrature VCO. IEEE Transactions on Microwave Theory and Techniques, 57, 344-351.
http://dx.doi.org/10.1109/TMTT.2008.2009901