Journal of Modern Physics
Vol.3 No.11(2012), Article ID:24388,6 pages DOI:10.4236/jmp.2012.311209
Symmetry Restoration by Acceleration
1Dipartimento di Fisica, Università di Catania, Catania, Italia
2INFN Sezione di Catania, Università di Catania, Catania, Italia
Email: castorina@ct.infn.it
Received August 6, 2012; revised September 9, 2012; accepted October 3, 2012
Keywords: Unruh Effect; Symmetry Breaking; Symmetry Restoration; Accelerated Frames
ABSTRACT
The restoration of spontaneous symmetry breaking for a scalar field theory for an accelerated observer is discussed by the one-loop effective potential calculation and by considering the effective potential for composite operators. Above a critical acceleration, corresponding to the critical restoration temperature, 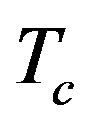 , for a Minkowski observer by Unruh relation, i.e.
, for a Minkowski observer by Unruh relation, i.e.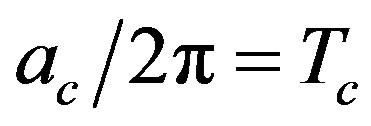 , the symmetry is restored. This result confirms other recent calculations in effective field theories that symmetry restoration can occur for an observer with an acceleration larger than some critical value. From the physical point of view, a constant acceleration mimics a gravitational field and the critical acceleration to restore the spontaneous symmetry breaking corresponds to a huge gravitational effect which prevents boson condensation.
, the symmetry is restored. This result confirms other recent calculations in effective field theories that symmetry restoration can occur for an observer with an acceleration larger than some critical value. From the physical point of view, a constant acceleration mimics a gravitational field and the critical acceleration to restore the spontaneous symmetry breaking corresponds to a huge gravitational effect which prevents boson condensation.
1. Introduction
In quantum field theory in flat space-time a spontaneously broken symmetry can be restored above some critical temperature [1-3]. On the other hand, whenever the background geometry is endowed with a black-hole or an event horizon, the related vacuum physically behaves like a thermal bath of quanta with a temperature, 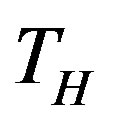 , proportional to the surface gravity [4]. Therefore one expects that symmetry restoration occurs also in strong enough gravitational fields, i.e. near a horizon [5]. On the other hand, the near horizon approximation of a black-hole metric corresponds to a Rindler metric, i.e. the metric of an observer with constant acceleration, a, equal to the surface gravity and Unruh [6,7] showed that for any accelerated observer there is an intrinsic thermal nature of the ground state: he/she feels a thermal bath with temperature
, proportional to the surface gravity [4]. Therefore one expects that symmetry restoration occurs also in strong enough gravitational fields, i.e. near a horizon [5]. On the other hand, the near horizon approximation of a black-hole metric corresponds to a Rindler metric, i.e. the metric of an observer with constant acceleration, a, equal to the surface gravity and Unruh [6,7] showed that for any accelerated observer there is an intrinsic thermal nature of the ground state: he/she feels a thermal bath with temperature . Moreover, a broken symmetry can be also restored if a classical external field strength (a magnetic field, for example) exceeds a critical value. Infact a particle coupled with an external field suffers a proper acceleration depending on the field strength.
. Moreover, a broken symmetry can be also restored if a classical external field strength (a magnetic field, for example) exceeds a critical value. Infact a particle coupled with an external field suffers a proper acceleration depending on the field strength.
The previous discussion clearly indicates that a restoration of the symmetry can occur for an observer with an acceleration larger than some critical value independently on the specific dynamical mechanism that produces the acceleration.
Indeed in Reference [8] it has been shown that for the Nambu-Jona Lasinio (NJL) model in an accelerated frame, the chiral symmetry (broken for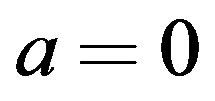 ) is restored for acceleration larger than a critical value
) is restored for acceleration larger than a critical value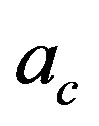 , corresponding to
, corresponding to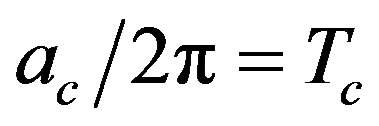 , where
, where 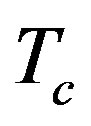 is the critical temperature for the restoration of the symmetry due to standard (flat space-time) thermal fluctuactions. In Reference [9] the behavior of quark and diquark condensates as seen by an accelerated observer has been studied and critical values of the acceleration for the restoration of chiral and color symmetries have been estimated. The dissociation of mesons, described as rotating string in Rindler space, by acceleration has been analyzed in ref. [10] with the conclusion that above a critical acceleration
is the critical temperature for the restoration of the symmetry due to standard (flat space-time) thermal fluctuactions. In Reference [9] the behavior of quark and diquark condensates as seen by an accelerated observer has been studied and critical values of the acceleration for the restoration of chiral and color symmetries have been estimated. The dissociation of mesons, described as rotating string in Rindler space, by acceleration has been analyzed in ref. [10] with the conclusion that above a critical acceleration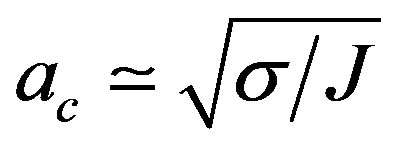 , where
, where  is the string tension and
is the string tension and  is the angular momentum, mesons undergo dissociation. In this letter we discuss the restoration of spontaneous symmetry breaking for
is the angular momentum, mesons undergo dissociation. In this letter we discuss the restoration of spontaneous symmetry breaking for 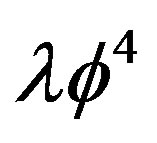 theory with similar results: above a critical acceleration, corresponding to the critical restoration temperature by Unruh relation, i.e.
theory with similar results: above a critical acceleration, corresponding to the critical restoration temperature by Unruh relation, i.e. 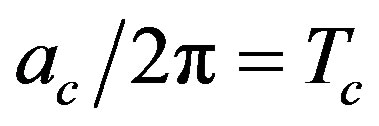 , the symmetry is restored. The calculations are based on the one-loop effective potential evaluation and its generalization for composite operators [11] (CJTmethod) which gives the resummation of an infinite set of diagrams by self-consistent gap equations. Initially (Sec.1) we recall briefly some general features of a scalar field theory in Rindler metric. In Section 2 we discuss the one-loop calculation of the effective potential for
, the symmetry is restored. The calculations are based on the one-loop effective potential evaluation and its generalization for composite operators [11] (CJTmethod) which gives the resummation of an infinite set of diagrams by self-consistent gap equations. Initially (Sec.1) we recall briefly some general features of a scalar field theory in Rindler metric. In Section 2 we discuss the one-loop calculation of the effective potential for 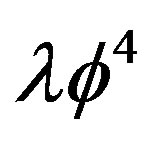 theory for an accelerated frame and the results by the CJT method. General considerations about the symmetry breaking due to acceleration and the Hawking-Unruh radiation are in the final section devoted to comments and conclusions. Lastly the effective action and effective potential methods for composite operators (CJT) are briefly reviewed in the appendix.
theory for an accelerated frame and the results by the CJT method. General considerations about the symmetry breaking due to acceleration and the Hawking-Unruh radiation are in the final section devoted to comments and conclusions. Lastly the effective action and effective potential methods for composite operators (CJT) are briefly reviewed in the appendix.
2. 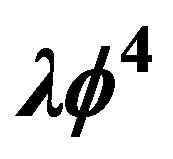 Theory in Rindler Metric
Theory in Rindler Metric
The action for the 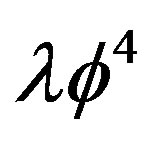 scalar theory in Rindler spacetimes [12] can be written as follow:
scalar theory in Rindler spacetimes [12] can be written as follow:
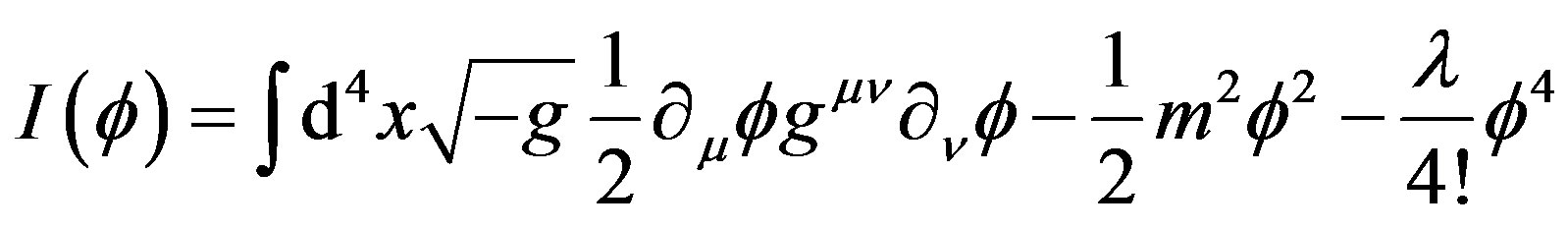 (1)
(1)
where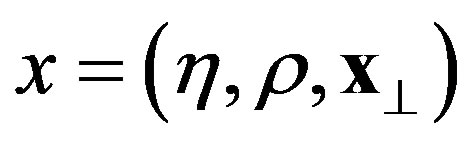 ,
, 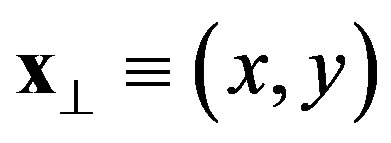 and the Rindler metric tensor
and the Rindler metric tensor 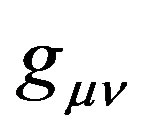 is given by:
is given by:
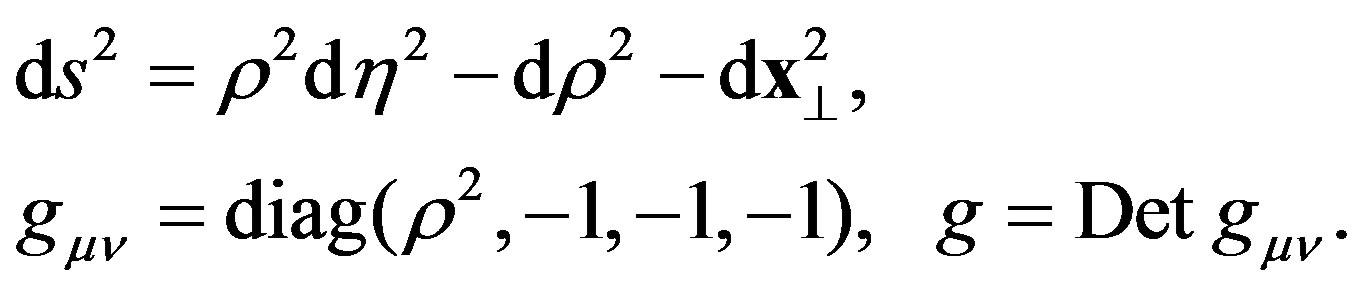 (2)
(2)
Since the two Rindler wedge are causally disconnected from each other [12] we restrict our consideration to the right Rindler wedge. Calculation in the left wedge can be performed in the same way. The Klein-Gordon equation for the scalar field 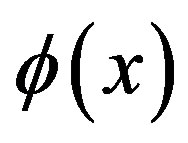 is
is
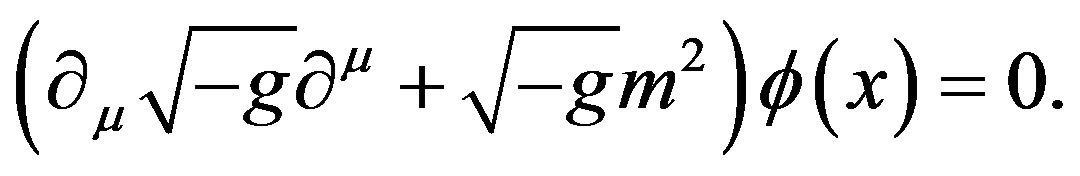 (3)
(3)
Taking the Fourier transform with respect to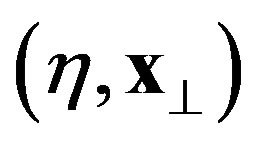 :
:
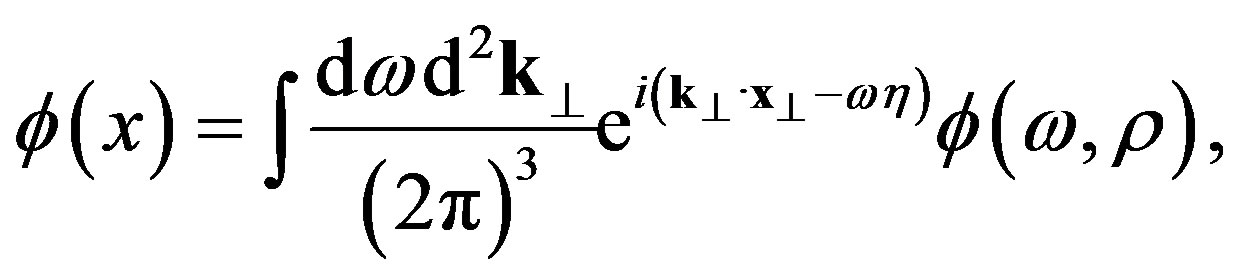 (4)
(4)
the normalized solution turns out
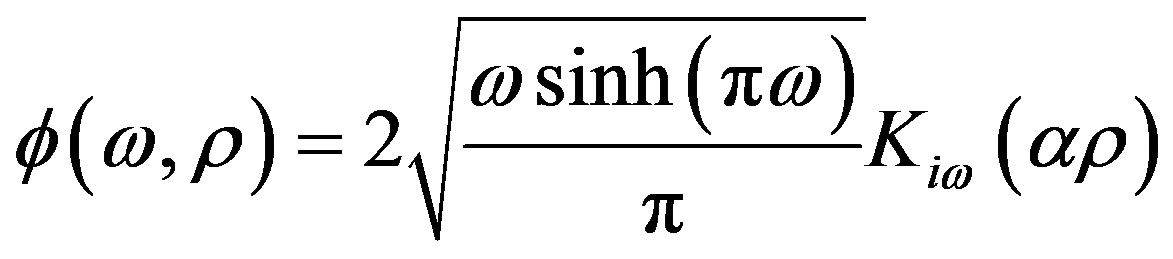 , (5)
, (5)
where is the modified Bessel function of second kind and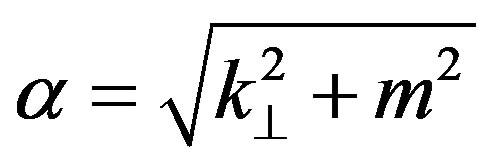 . The two-point Green’s function of the free scalar field in the right Rindler wedge
. The two-point Green’s function of the free scalar field in the right Rindler wedge , is defined by the equation:
, is defined by the equation:
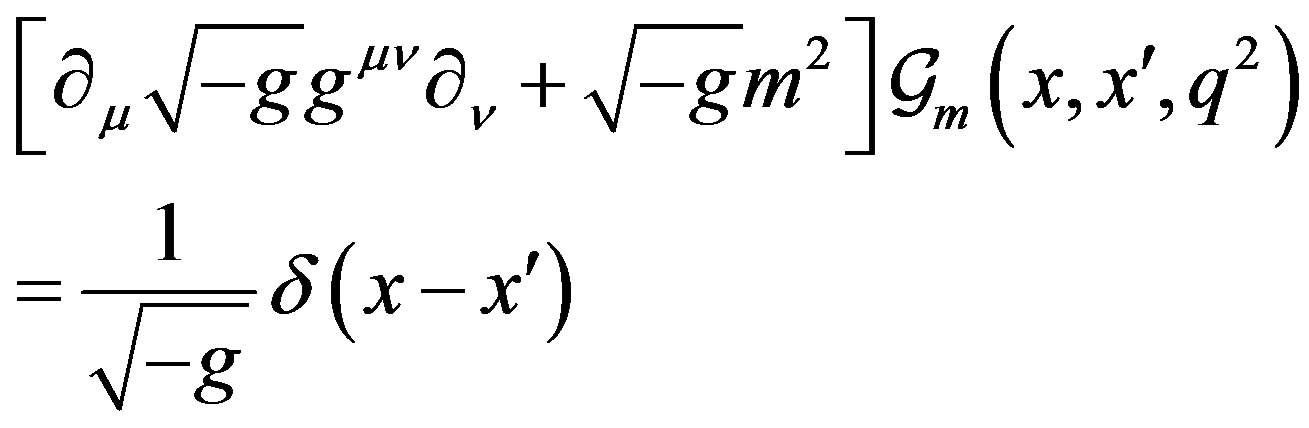 (6)
(6)
The Fourier transform of 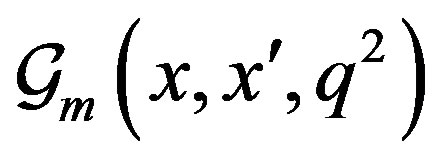 with respect to
with respect to  is given by
is given by
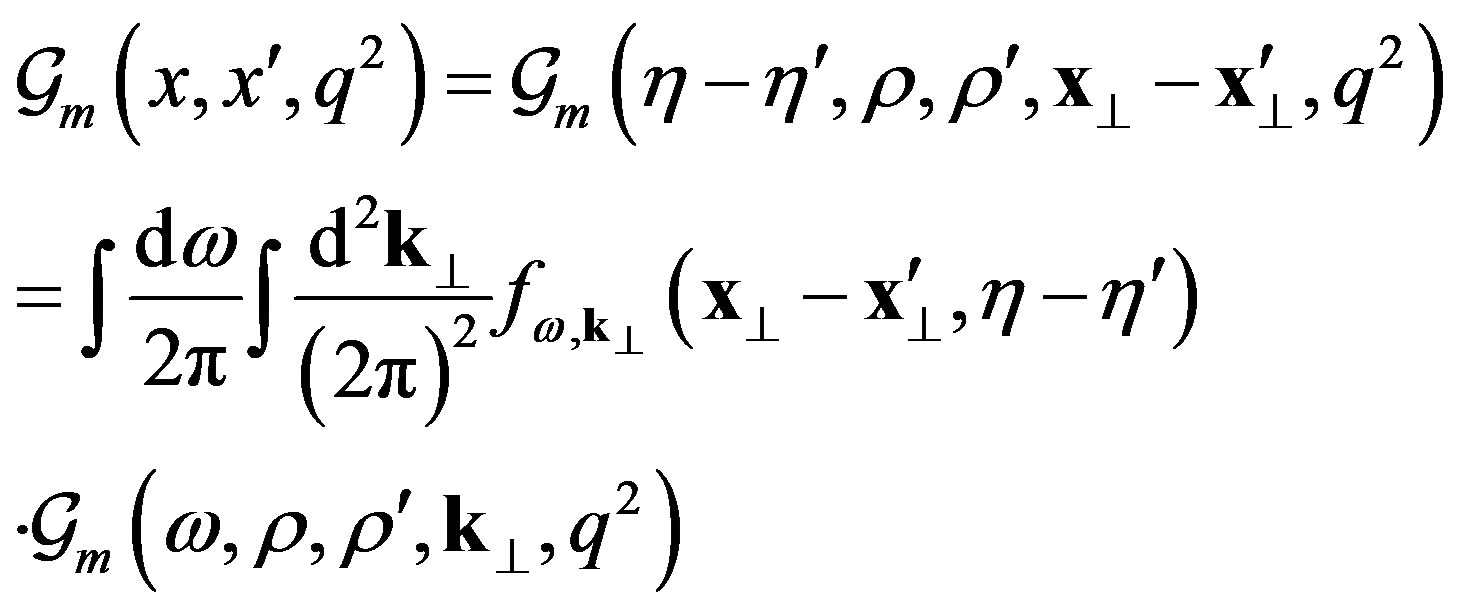 (7)
(7)
where
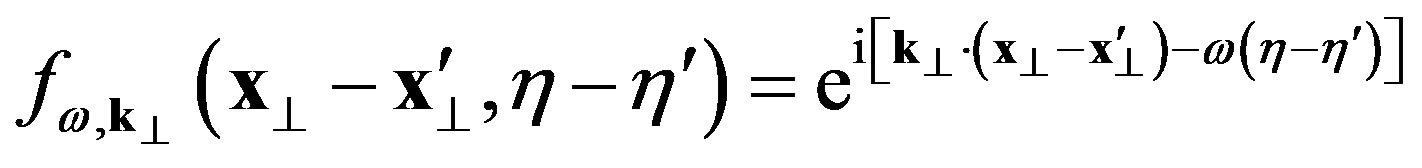 . (8)
. (8)
By substituting back into Equation (6) one finds:
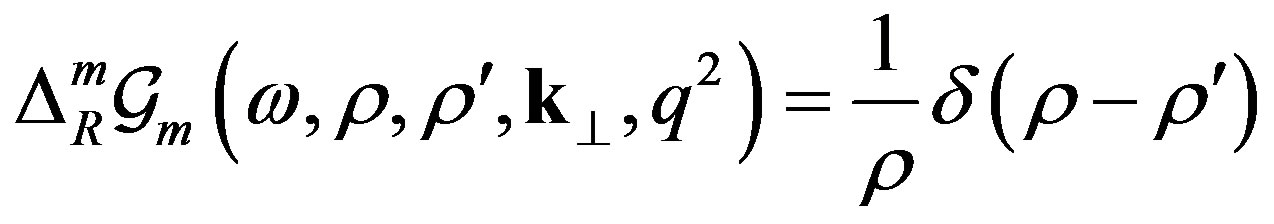 (9)
(9)
where
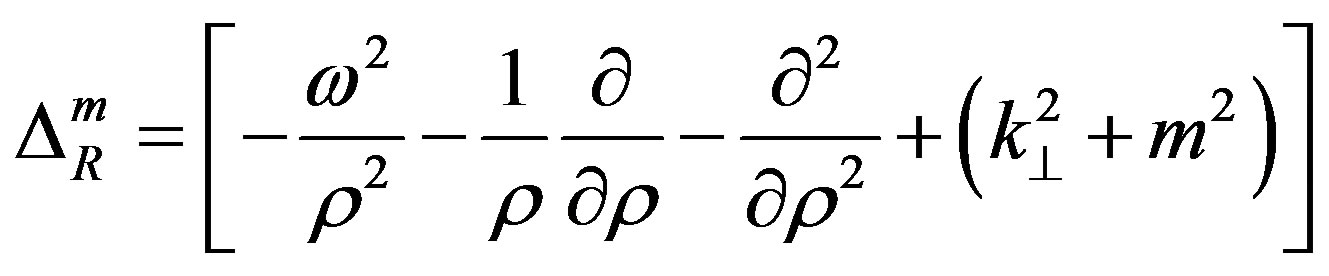 . (10)
. (10)
The world line in Rindler coordinates of a uniformly accelerated observer with proper constant acceleration 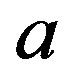 is given as,
is given as,
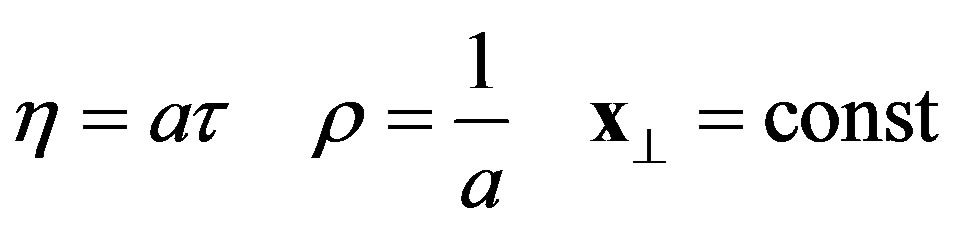 (11)
(11)
and it has been generally proved [7] that Euclidean two point functions in Rindler coordinates are periodic in the direction of time with period a.
Since the Euclidean Rindler spacetime has a singularity at 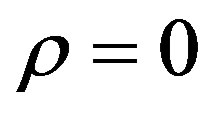 one requires that the period of the imaginary time is
one requires that the period of the imaginary time is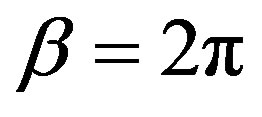 . With this particular choice the Euclidean formalism in Rindler coordinates coincides with the finite temperature Matsubara formalism and therefore the following substitutions will be necessary in evaluating the effective potential in the next sections:
. With this particular choice the Euclidean formalism in Rindler coordinates coincides with the finite temperature Matsubara formalism and therefore the following substitutions will be necessary in evaluating the effective potential in the next sections:
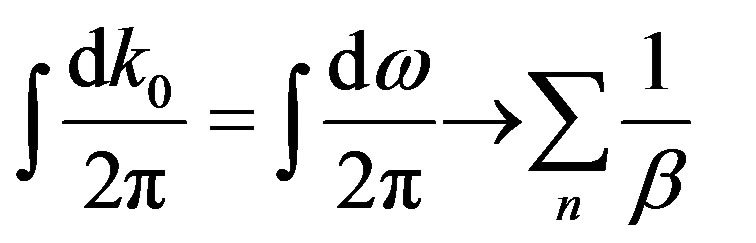 (12)
(12)
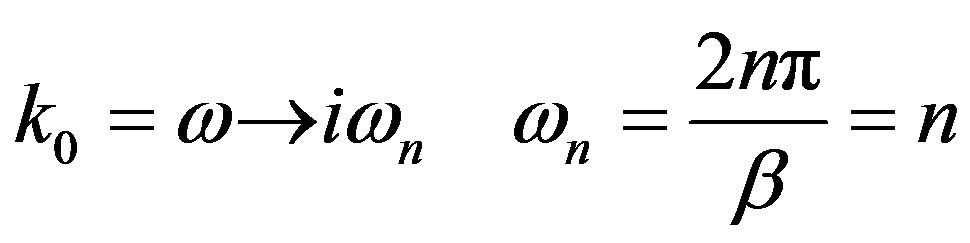 (13)
(13)
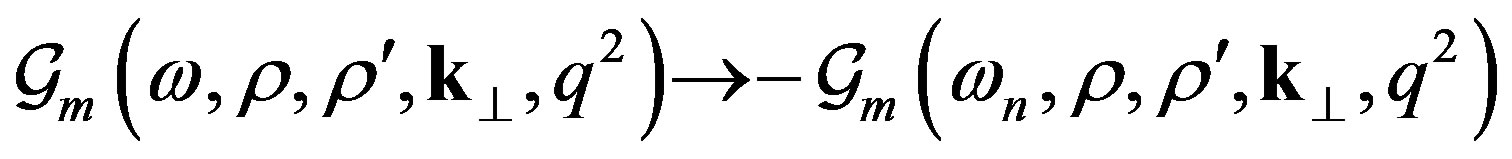 . (14)
. (14)
3. Effective Potential for Accelerated Observer
Let us now study the effective potential for a Rindler observer when for a Minkowski observer the effective potential is assumed to possess a symmetry breaking solution. For classical constant field configuration, 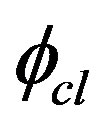 , the one loop effective action in Rindler coordinates turns out to be:
, the one loop effective action in Rindler coordinates turns out to be:
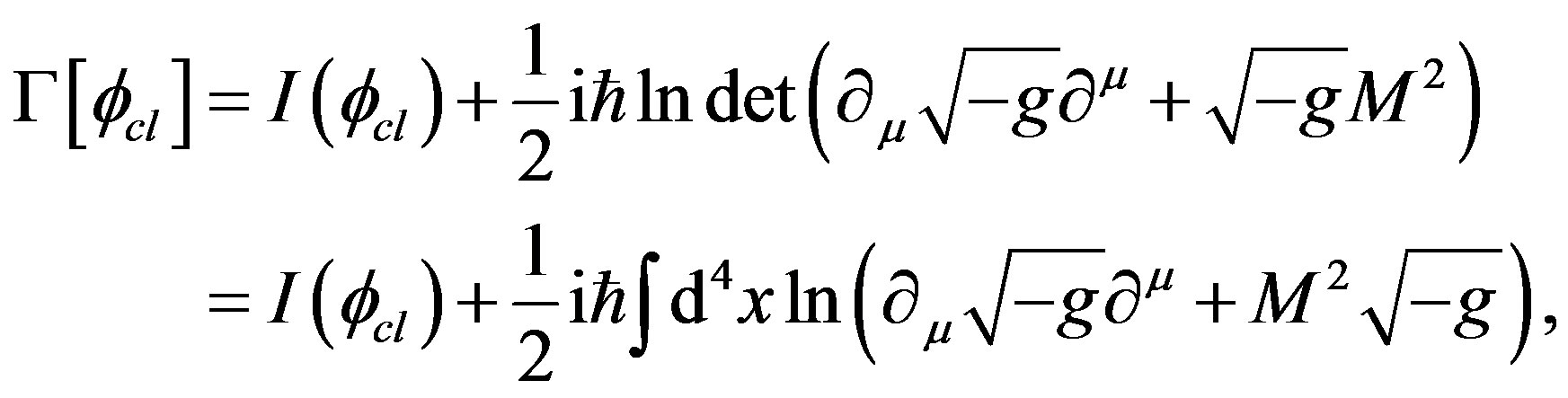 (15)
(15)
where 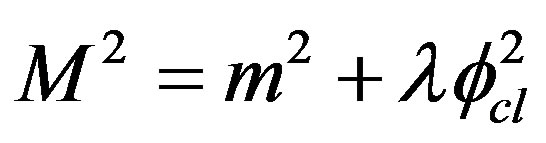 and
and 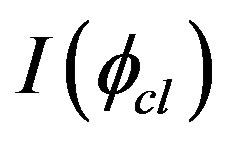 is given by
is given by
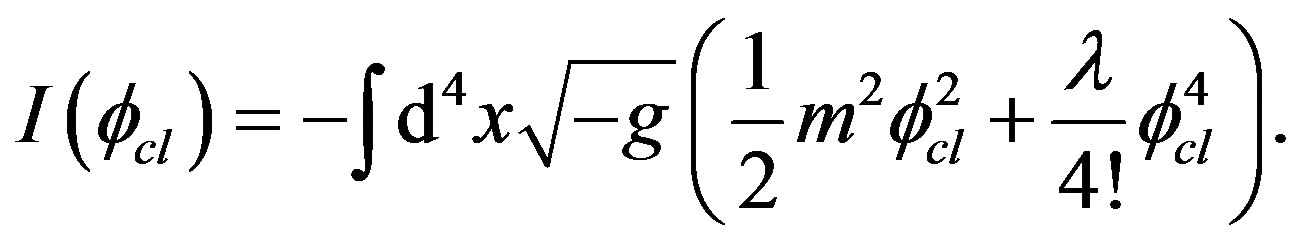 (16)
(16)
The effective potential (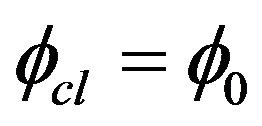 ,
,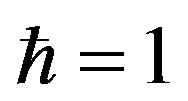 ) is defined as
) is defined as
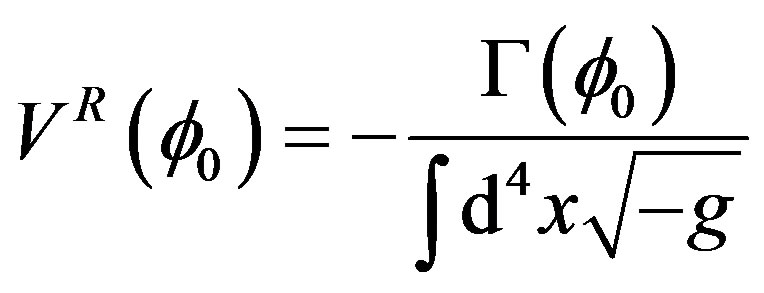 (17)
(17)
and by the following relation,
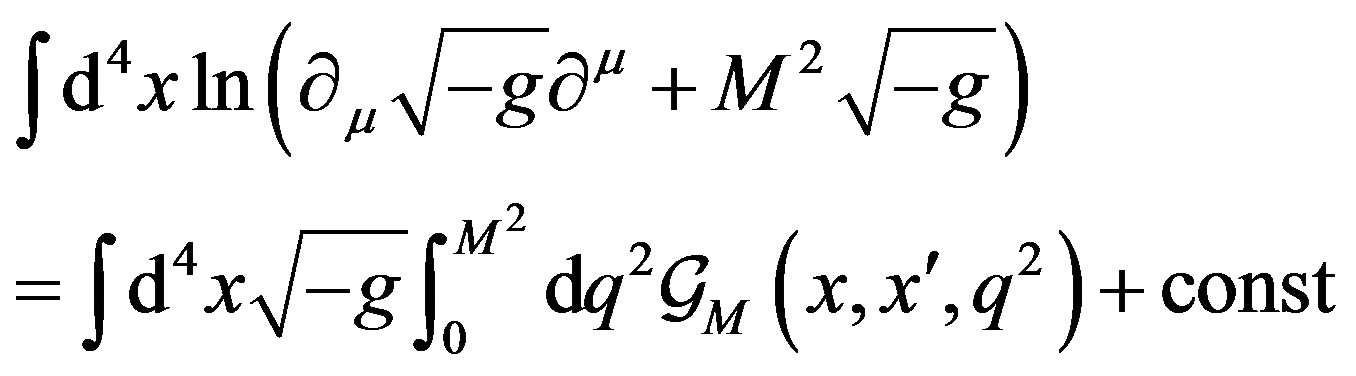 (18)
(18)
where 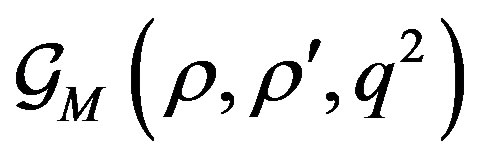 is defined by previous Equations (7)-(10) with the substitution,
is defined by previous Equations (7)-(10) with the substitution, 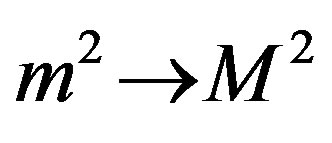 it turns out to be
it turns out to be
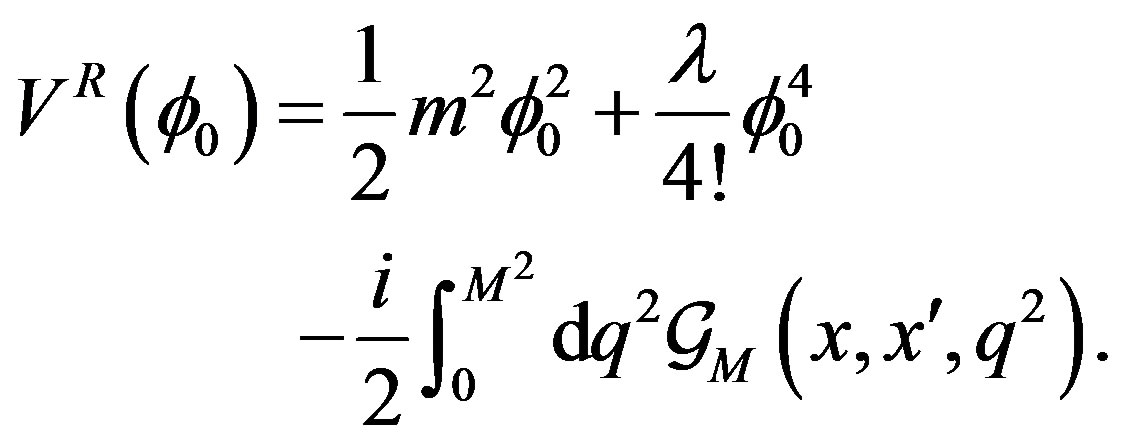 (19)
(19)
In Euclidean space with the periodic boundary condition in Equations (12) and (13) and by introducing the Fourier transform of the Green’s function, Equation (7), the previous equation gives
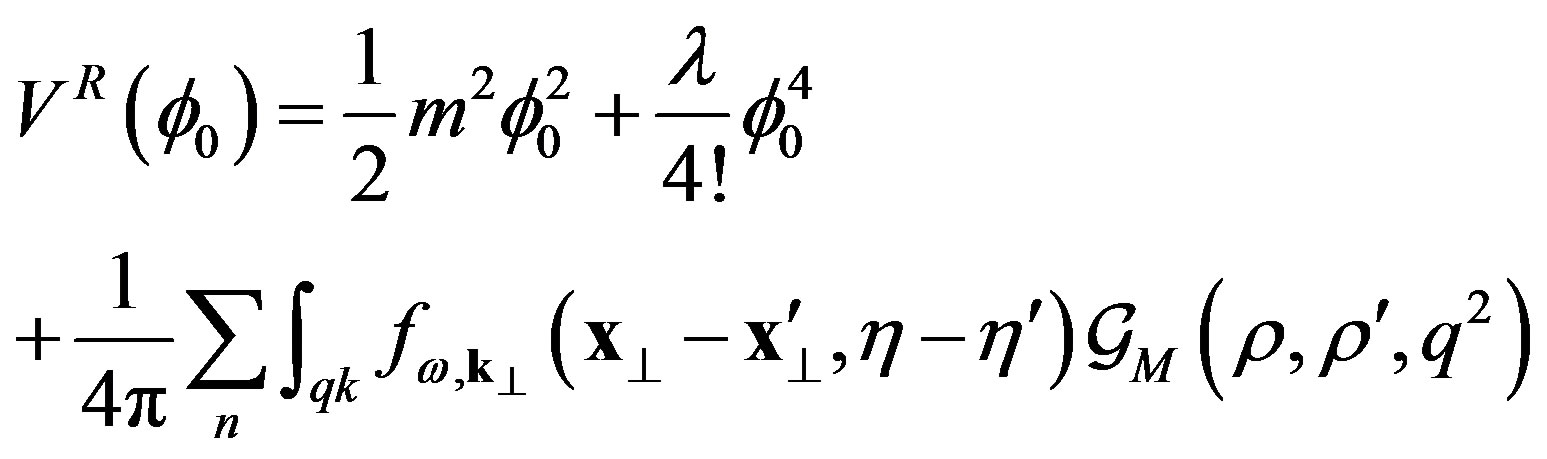 (20)
(20)
where
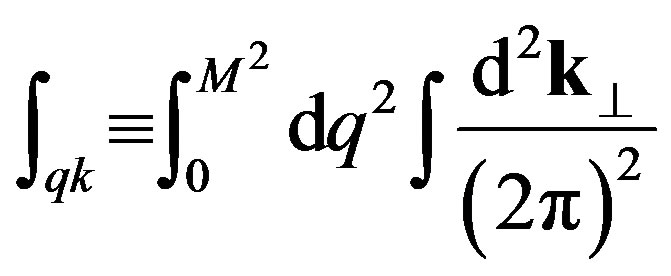 (21)
(21)
and 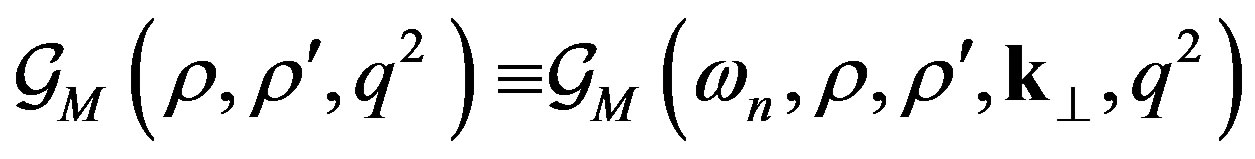 is now solution of the equation
is now solution of the equation
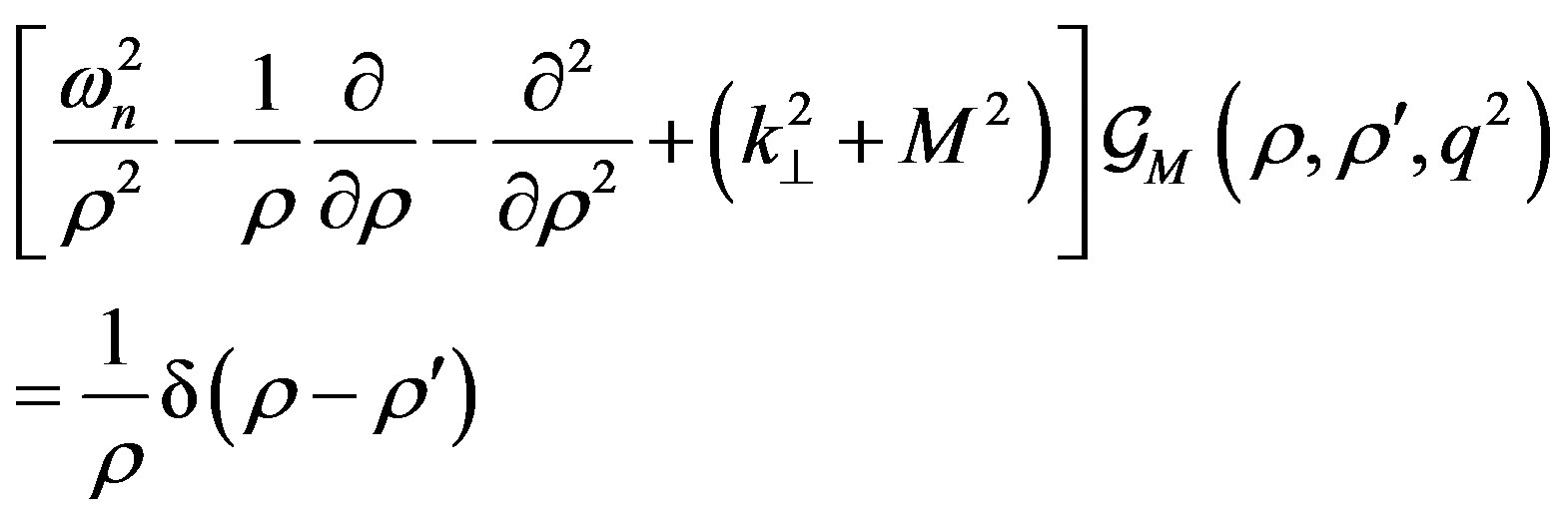 (22)
(22)
which, according to Equation (5) can be written as
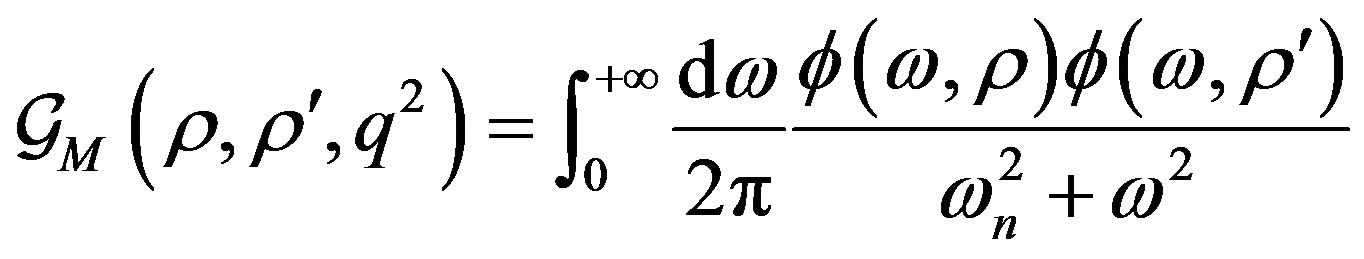 (23)
(23)
Since the world line in Rindler coordinates of a uniformly accelerated observer with proper constant acceleration 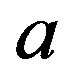 is given by Equation (11), one sets
is given by Equation (11), one sets 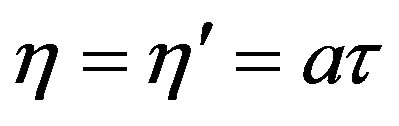 and
and 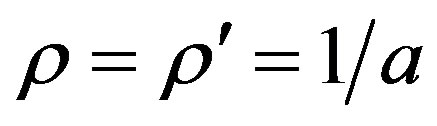 and by changing the integration variable in Equation (23) from
and by changing the integration variable in Equation (23) from 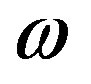 to
to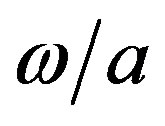 , it turns out
, it turns out
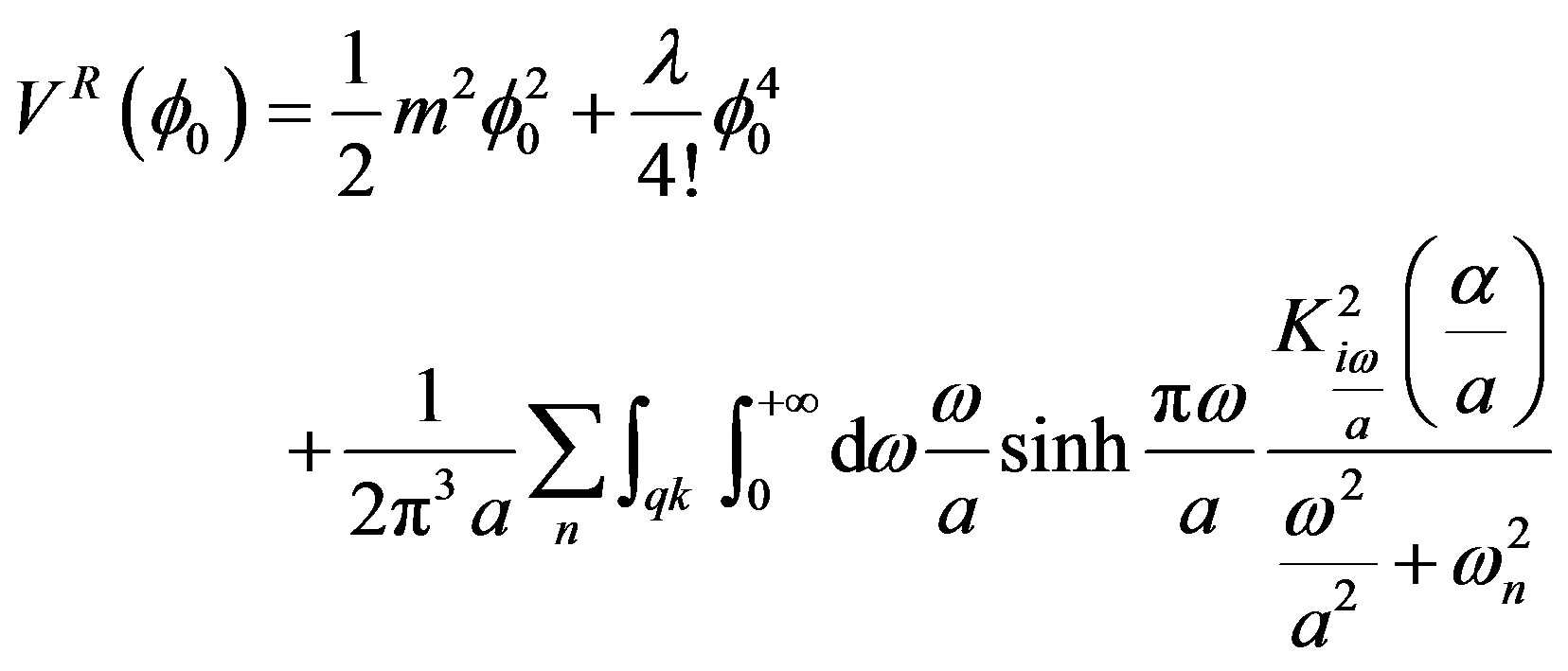 (24)
(24)
By performing the sum on the Matsubara frequencies the final result for the effective potential is
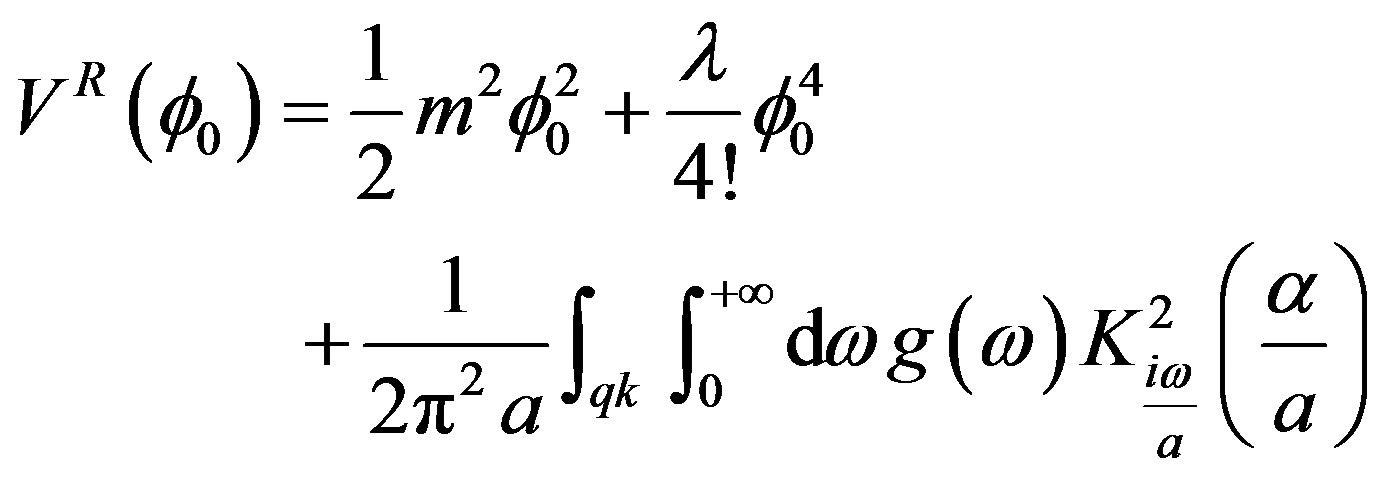 (25)
(25)
with  and
and 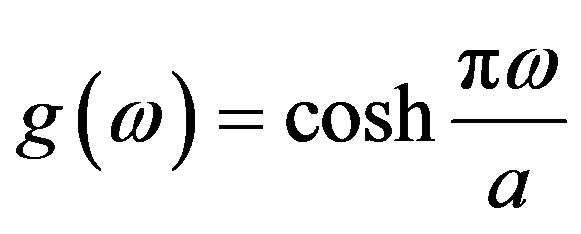
In order to calculate the critical acceleration 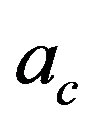 for symmetry restoration we will impose the following condition [3]:
for symmetry restoration we will impose the following condition [3]:
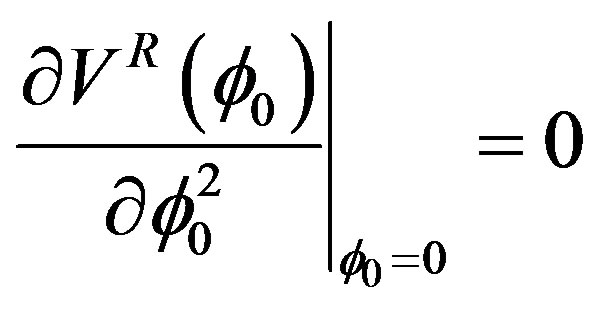 (26)
(26)
which gives
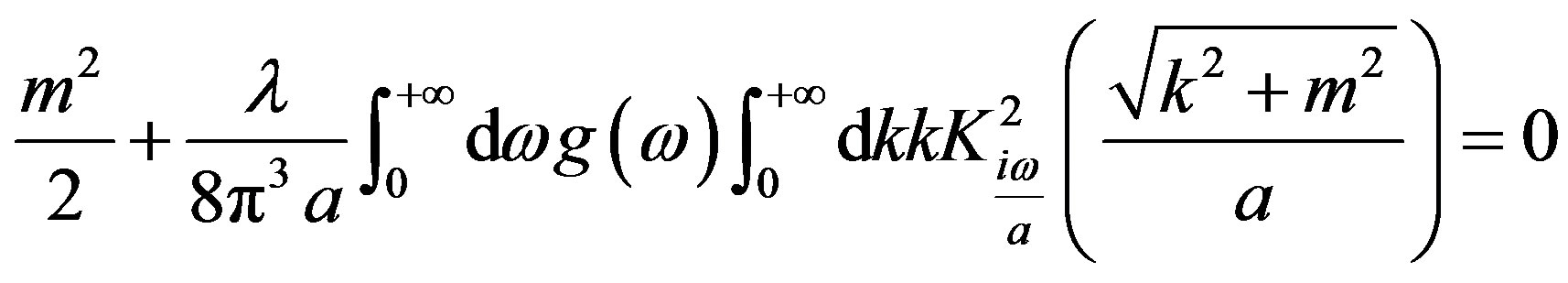 , (27)
, (27)
where we set 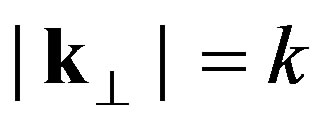 for notation convenience. The computation of the integrals is straithforward and one gets
for notation convenience. The computation of the integrals is straithforward and one gets
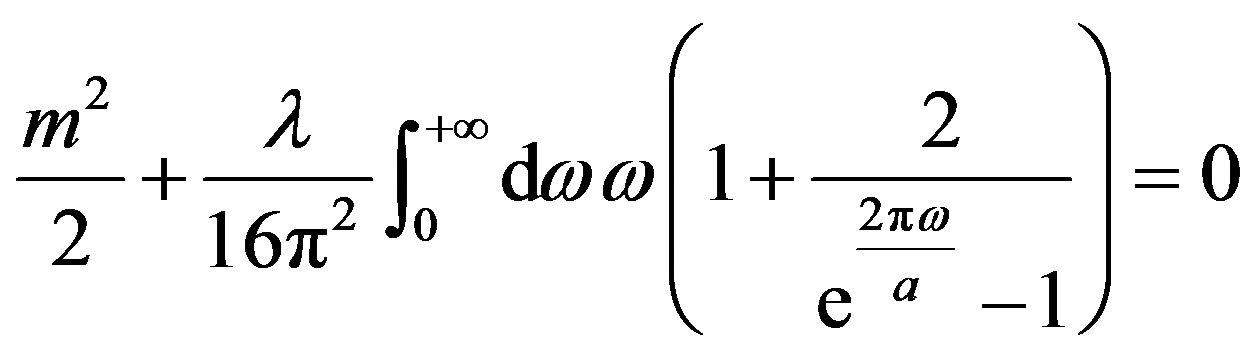 , (28)
, (28)
in complete analogy with the finite temperature case [3]. Indeed by defining the renormalized mass to cancel the quadratic divergence
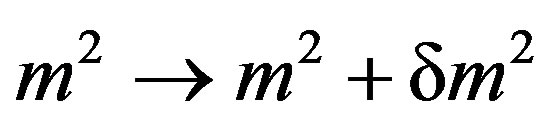 (29)
(29)
the critical acceleration is obtained by the equation
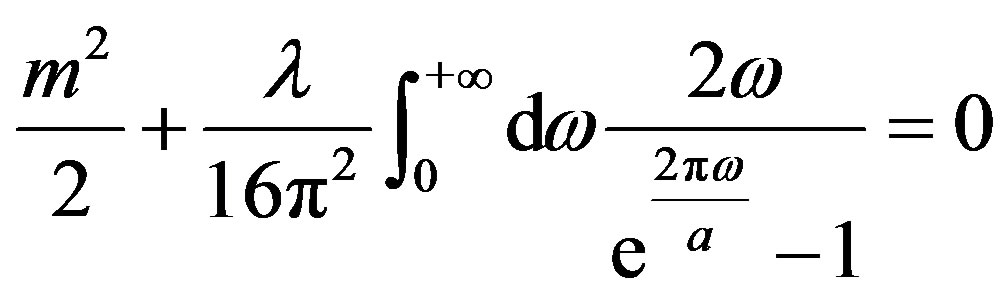 (30)
(30)
which, for large acceleration, gives
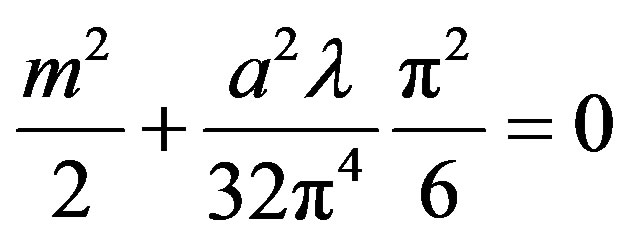 (31)
(31)
i.e.
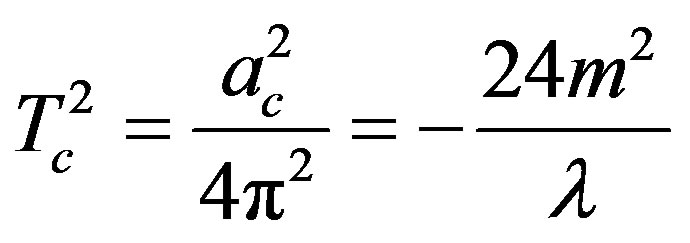 (32)
(32)
in agreement with the one-loop calculation in Minkowski space-time at finite temperature [3] (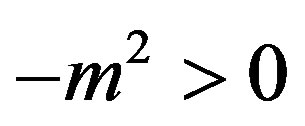 ). The previous expression in brackets might be confusing. Hence let me briefly clarify it. As we know the phenomenon of spontaneous symmetry breaking is characterized by the existence of a non-vanishing vacuum expectation value of the field
). The previous expression in brackets might be confusing. Hence let me briefly clarify it. As we know the phenomenon of spontaneous symmetry breaking is characterized by the existence of a non-vanishing vacuum expectation value of the field 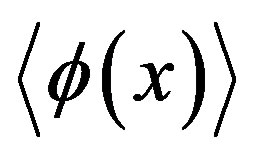 which minimize the effective potential
which minimize the effective potential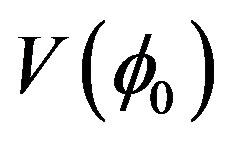 . The (renormalized) mass square
. The (renormalized) mass square 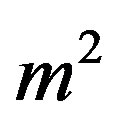 is defined as the functional second derivative of the effective action
is defined as the functional second derivative of the effective action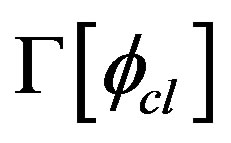 . For classical constant field configurations
. For classical constant field configurations 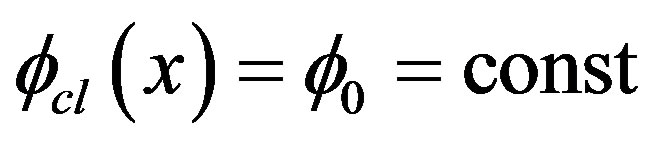 we can define the effective potential as we did in Equation (17) and the mass is given by:
we can define the effective potential as we did in Equation (17) and the mass is given by:
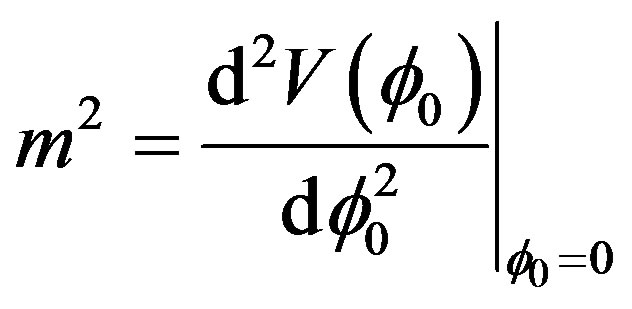 . (33)
. (33)
If the symmetry is unbroken then 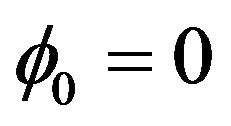 is a minimum for
is a minimum for 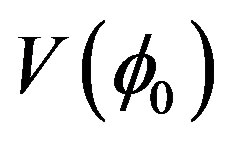 and the second derivative is positive. However in our case the symmetry is spontaneously broken and the effective potential develops two symmetric non-vanishing minima while
and the second derivative is positive. However in our case the symmetry is spontaneously broken and the effective potential develops two symmetric non-vanishing minima while 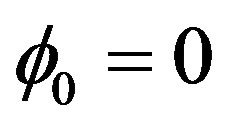 becomes a maximum. Then the fact that
becomes a maximum. Then the fact that 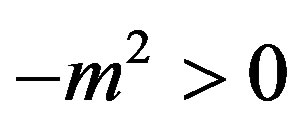 does not mean that the mass square is negative but simply tells us that we are computing the mass square in the wrong vacuum state i.e. in a field configuration which, because of symmetry breaking, is not the true vacuum state (the minimum) anymore (indeed it is a maximum and hence the second derivative is negative).
does not mean that the mass square is negative but simply tells us that we are computing the mass square in the wrong vacuum state i.e. in a field configuration which, because of symmetry breaking, is not the true vacuum state (the minimum) anymore (indeed it is a maximum and hence the second derivative is negative).
Although the final result is as expected, the calculation in not entirely trivial. Moreover the determination of the critical acceleration from one loop effective potential suffers the same infrared problem of the finite temperature calculation related with the mode . As well known, in finite temperature field theory a reliable evaluation of the critical temperature requires the resummation of an infinite subset of diagrams [3]. This can be more easily done by considering the effective potential for composite operators (CJT) [11], extensively applied at finite temperature [13], since the relevant, infinite, subset of diagrams is automatically resummed by the gap equations corresponding to the minimum conditions of the effective potential with respect to the relevant physical parameters in the theory. In the analysis of the spontaneous symmetry breaking and its restoration for
. As well known, in finite temperature field theory a reliable evaluation of the critical temperature requires the resummation of an infinite subset of diagrams [3]. This can be more easily done by considering the effective potential for composite operators (CJT) [11], extensively applied at finite temperature [13], since the relevant, infinite, subset of diagrams is automatically resummed by the gap equations corresponding to the minimum conditions of the effective potential with respect to the relevant physical parameters in the theory. In the analysis of the spontaneous symmetry breaking and its restoration for 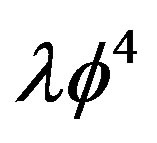 theory by CJT method in the Hartree-Fock approximation (i.e. by considering the lowest order contribution to the gap equation) the relevant operators are
theory by CJT method in the Hartree-Fock approximation (i.e. by considering the lowest order contribution to the gap equation) the relevant operators are 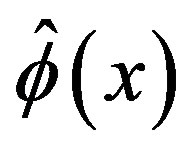 and
and 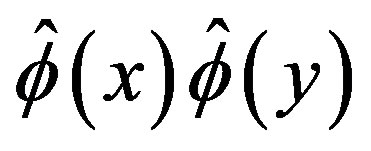 and the corresponding parameters are the vacuum expectation value of the field and the mass in the two-point function. Calculations at finite temperature have been carried out in [14]. Since the gap equation in the Hartree-Fock approximation correspond to one-loop selfconsistent calculation of the self-energy (see [14] for details) from our previous, explicit, oneloop calculation and from the complete analogy of the Green’s functions between a Minkowski observer at finite temperature and an accelerated observer with
and the corresponding parameters are the vacuum expectation value of the field and the mass in the two-point function. Calculations at finite temperature have been carried out in [14]. Since the gap equation in the Hartree-Fock approximation correspond to one-loop selfconsistent calculation of the self-energy (see [14] for details) from our previous, explicit, oneloop calculation and from the complete analogy of the Green’s functions between a Minkowski observer at finite temperature and an accelerated observer with 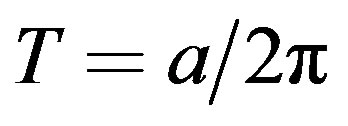 [7], it follows that a more reliable evaluation of the critical acceleration
[7], it follows that a more reliable evaluation of the critical acceleration 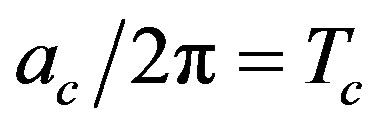 with respect to the one-loop result in Equation (32) can be obtained by following the same analysis of [14]. However the most interesting aspect is not the exact value of the critical acceleration but the restoration of the symmetry for an accelerated observer (see [7], Section 4, for a different point of view).
with respect to the one-loop result in Equation (32) can be obtained by following the same analysis of [14]. However the most interesting aspect is not the exact value of the critical acceleration but the restoration of the symmetry for an accelerated observer (see [7], Section 4, for a different point of view).
4. Comments and Conclusions
The restoration of chiral and color symmetries in the Nambu Jona-Lasinio model for an observer with a costant acceleration above a critical value [8,9] and the calculation performed in the previous section clearly indicate that one can restore broken symmetries by acceleration. Although the technical aspects of the previous calculations are sound, the physical mechanism of the restoration is unclear if one does not recall that a constant acceleration is locally equivalent to a gravitational field. The critical acceleration to restore the spontaneous symmetry breaking corresponds to a huge gravitational effect which prevents boson condensation as in the case of a non relativistic, ideal Bose gas [15].
More generally, the acceleration associated with the Hawking-Unruh temperature (and radiation) due to the observed gravitational fields is too small to produce measurable effects. There are very interesting attempts to find gravity-analogue of the Hawking-Unruh radiation [16,17] and, in our opinion, high energy particle physics seems the more promising sector to observe this effect. Indeed, a temperatute 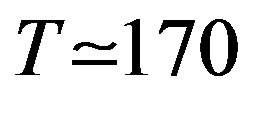 MeV, corresponding to an acceleration
MeV, corresponding to an acceleration 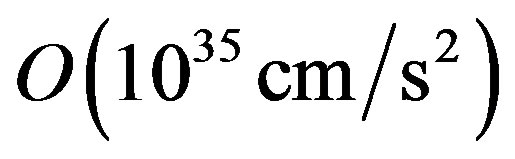 can be reached in relativistic heavy ion collisions and the hadronic production can be understood as Hawking-Unruh radiation in Quantum Chromodynamics [18-20].
can be reached in relativistic heavy ion collisions and the hadronic production can be understood as Hawking-Unruh radiation in Quantum Chromodynamics [18-20].
5. Acknowledgements
The authors thank H. Satz and D. Zappalà for useful comments.
REFERENCES
- D. A. Kirzhnits and A. D. Linde, “Macroscopic Consequence of the Weinberg Model,” Physics Letters B, Vol. 42, No. 4, 1972, pp. 471-474. doi:10.1016/0370-2693(72)90109-8
- S. Weinberg, “Gauge and Global Symmetry at High Temperature,” Physical Review D, Vol. 9, No. 12, 1974, pp. 3357-3378. doi:10.1103/PhysRevD.9.3357
- L. Dolan and R. Jackiw, “Symmetry Behavior at Finite Temperature,” Physical Review D, Vol. 9, No. 12, 1974, pp. 3320-3341. doi:10.1103/PhysRevD.9.3320
- S. W. Hawking, “Particle Creation by Black Holes,” Communications in Mathematical Physics, Vol. 43, No. 3, 1975, pp. 199-220. doi:10.1007/BF02345020
- G. Denardo and E. Spallucci, “Symmetry Restoration in Conformally Flat Metric,” Nuovo Cimento A, Vol. 64, No, 1, 1981, pp. 15-26. doi:10.1007/BF02773363
- W. G. Unruh, “Notes on Black Hole Evaporation,” Physical Review D, Vol. 14, No. 4, 1976, p. 870. doi:10.1103/PhysRevD.14.870
- W. G. Unruh and N. Weiss, “Acceleration Radiation in Interacting Field Theories,” Physical Review D, Vol. 29, No. 8, 1984, p. 1656. doi:10.1103/PhysRevD.29.1656
- T. Ohsaku, “Dynamical Chiral Symmetry Breaking and its Restoration for an Accelerated Observer,” Physics Letters B, Vol. 599, No. 1-2, 2004, pp. 102-110. doi:10.1016/j.physletb.2004.08.019
- D. Ebert and V. Ch. Zhukovsky, “Restoration of Dynamically Broken Chiral and Color Symmetry for an Accelerated Observer,” Physics Letters B, Vol. 645, No. 2-3, 2007, pp. 267-274. doi:10.1016/j.physletb.2006.12.013
- K. Peeters and M. Zamaklar, “Dissociation by Acceleration,” Journal of High Energy Physics, Vol. 801, 2008, p. 38. doi:10.1088/1126-6708/2008/01/038
- J. M. Cornwall, R. Jackiw and E. Tomboulis, “Effective Action for Composite Operators,” Physical Review D, Vol. 10, No. 8, 1974, pp. 2428-2445. doi:10.1103/PhysRevD.10.2428
- L. C. B. Crispino, A. Higuchi and G. E. A. Matsas, “The Unruh Effect and Its Applications,” Reviews of Modern Physics, Vol. 80, No. 3, 2008, pp. 787-838. doi:10.1103/RevModPhys.80.787
- G. Amelino-Camelia and S.-Y. Pi, “Selfconsistent Improvement of the Finite Temperature Effective Potential,” Physical Review D, Vol. 47, No. 6, 1993, pp. 2356-2362. doi:10.1103/PhysRevD.47.2356
- P. Castorina, M. Consoli and D. Zappalà, “Finite Temperature Hartree-Fock Approximation to λφ4 Theory,” Physics Letters B, Vol. 201, No. 1, 1988, pp. 90-94. doi:10.1016/0370-2693(88)90086-X
- R. M. Cavalcanti, P. Giacconi, G. Pupillo and R. Soldati, “Bose-Einstein Condensation in the Presence of a Uniform Field and a Point-Like Impurity,” Physical Review A, Vol. 65, No. 5, 2002, pp. 53-60. doi:10.1103/PhysRevA.65.053606
- C. Barcelo, S. Liberati and M. Visser, “Analogue Gravity,” Living Reviews in Relativity, Vol. 4, No. 3, 2011, p. 12. http://www.livingreviews.org/lrr-2011-3
- A. Iorio and G. Lambiase, “The Hawking-Unruh Phenomenon on Graphene,” Physics Letters B, Vol. 716, No. 2, 2012, pp. 334-337. doi:10.1016/j.physletb.2012.08.023
- P. Castorina, D. Kharzeev and H. Satz, “Thermal Hadronization and Hawking-Unruh Radiation in QCD,” The European Physical Journal, Vol. 52, No. 1, 2007, pp. 187-201. doi:10.1140/epjc/s10052-007-0368-6
- F. Becattini, P. Castorina, A. Milov and H. Satz, “Prediction of Hadron Abundances in pp Collision at LHC,” Journal of Physics G, Vol. 38, No. 2, p. 25. doi:10.1088/0954-3899/38/2/025002
- P. Castorina, R. V. Gavai and H. Satz, “The QCD Phase Structure at High Baryon Density,” The European Physical Journal, Vol. 69, No. 1-2, 2010, pp. 169-178. doi:10.1140/epjc/s10052-011-1653-y
Appendix: The Effective Action for Composite Operators
An efficient way to perform systematic selective summations is to use the method of the effective action for composite operators [11]. In this case, the effective action is the generating functional of the two-particle ireducible (2PI) vacuum graphs (a graph is called two-particle irreducible if it does not become disconnected upon opening two lines). Now, the effective action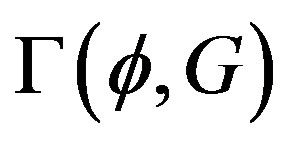 , depends not only on
, depends not only on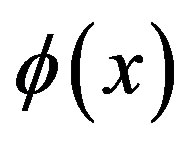 , but on
, but on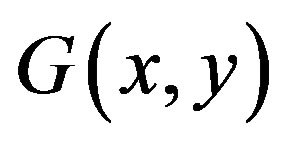 , as well. These two quantities are to be realized as the possible expectation values of a quantum field
, as well. These two quantities are to be realized as the possible expectation values of a quantum field 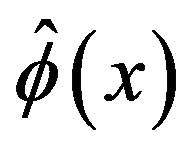 and as the time ordered product of the field operator
and as the time ordered product of the field operator 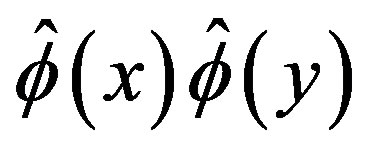 respectively. There is an advantage in using the CJT method to calculate the effective potential in certain approximations as is, for example, the Hartree-Fock approximation of the
respectively. There is an advantage in using the CJT method to calculate the effective potential in certain approximations as is, for example, the Hartree-Fock approximation of the 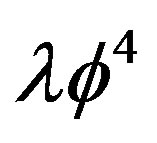 theory. Indeed, if we use an ansatz for a dressed propagator, we need to evaluate only the double bubble graph in Figure 1 (with lines representing dressed propagators), instead of summing the infinite class of daisy and super-daisy graphs. In order to define the effective action for composite operators, we can follow a path analogous to the one leading to the ordinary effective action. The essential difference is that the partition function depends also on a bilocal source
theory. Indeed, if we use an ansatz for a dressed propagator, we need to evaluate only the double bubble graph in Figure 1 (with lines representing dressed propagators), instead of summing the infinite class of daisy and super-daisy graphs. In order to define the effective action for composite operators, we can follow a path analogous to the one leading to the ordinary effective action. The essential difference is that the partition function depends also on a bilocal source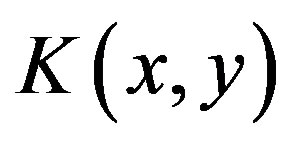 , in addition to the local source
, in addition to the local source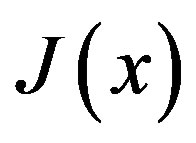 . As an example, we consider the
. As an example, we consider the 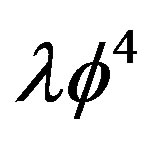 theory with Lagrangian:
theory with Lagrangian:
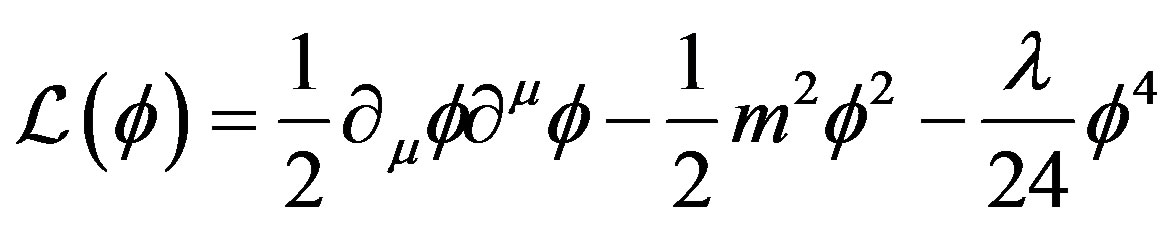 (34)
(34)
According [11], the generating functional for the Green functions in the presence of sources 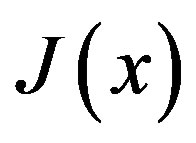 and
and 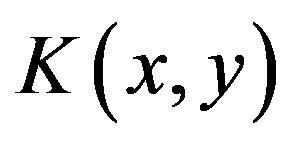 is given by (we set
is given by (we set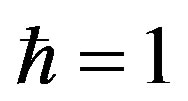 )
)
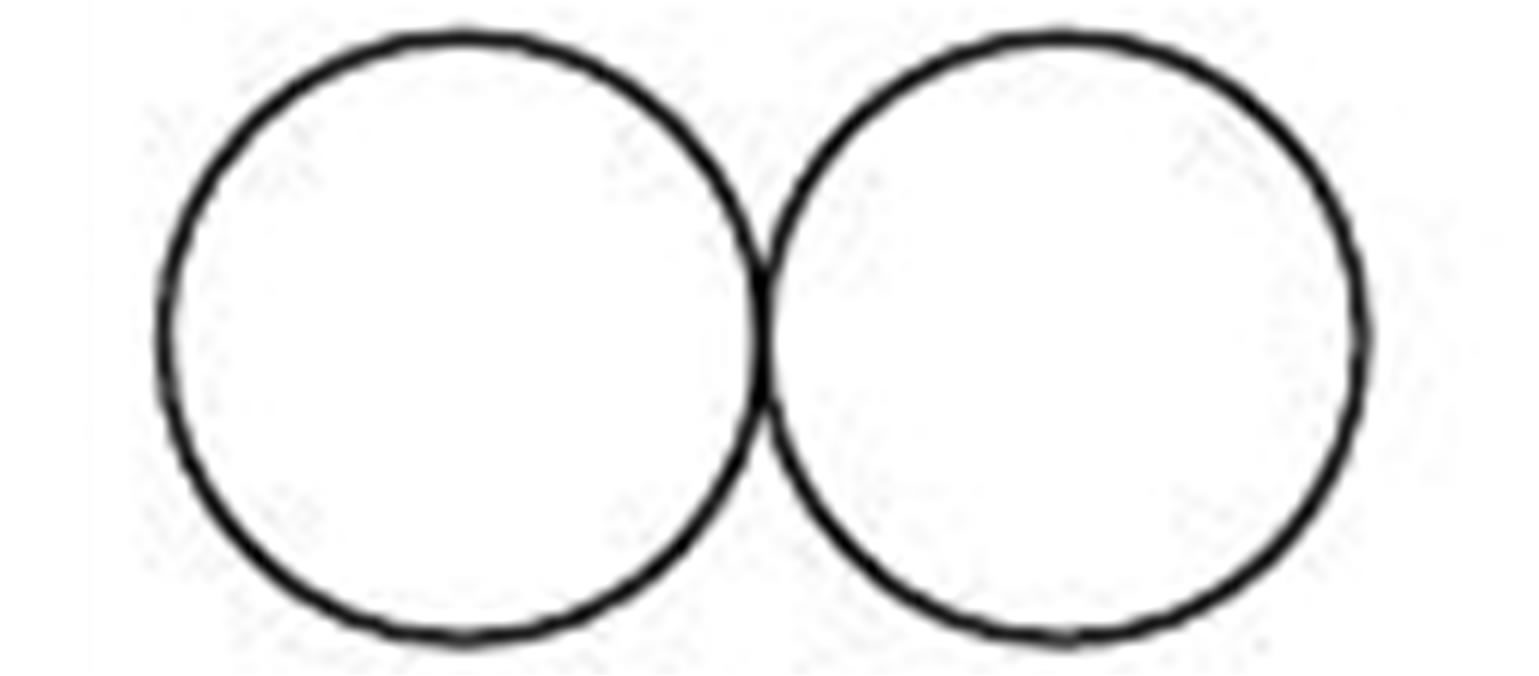
Figure 1. The double bubble graph contributing to the effective potential in the CJT method. The lines represent dressed propagators G(x, y).
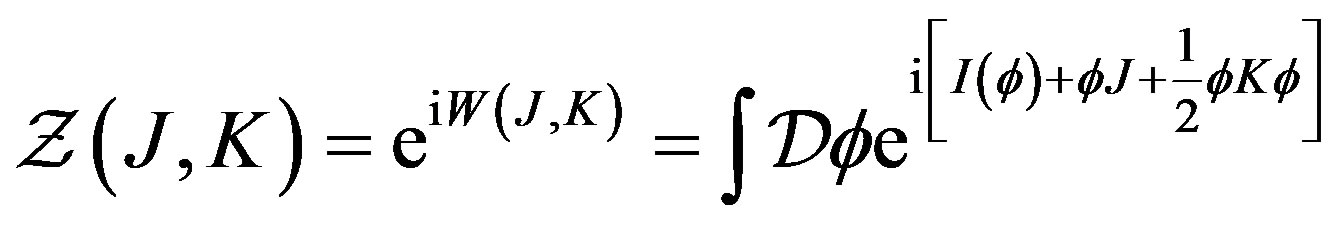 (35)
(35)
where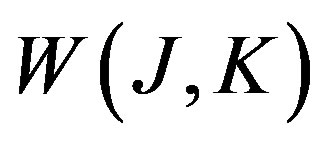 , is the generating functional for the connected Green functions, while
, is the generating functional for the connected Green functions, while 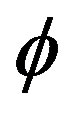 is the classical action. The effective action for composite operators
is the classical action. The effective action for composite operators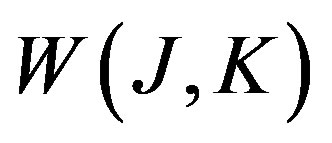 , is obtained through a double Legendre transformation of
, is obtained through a double Legendre transformation of 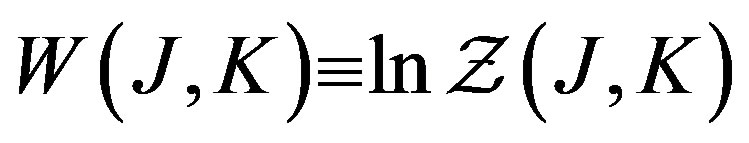
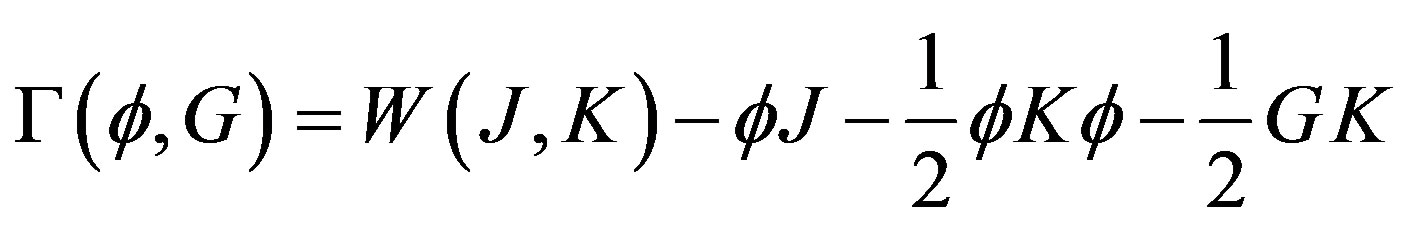 (36)
(36)
Physical processes correspond to vanishing sources, so the stationarity conditions which determine the expectation value of the field 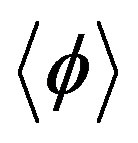 and the (dressed) propagator
and the (dressed) propagator 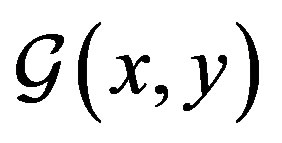 are given by
are given by
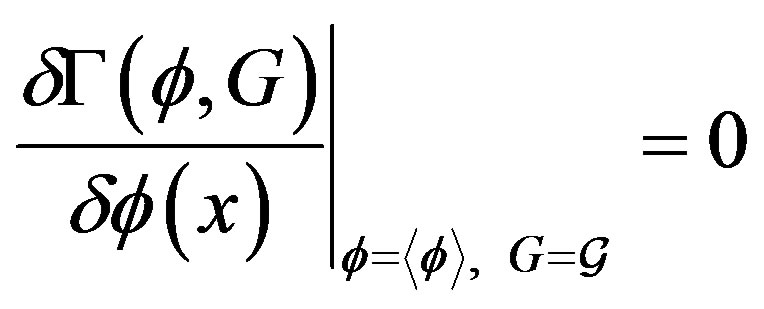 (37)
(37)
 (38)
(38)
As it was shown by in [11], the effective action 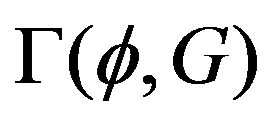 is given by
is given by
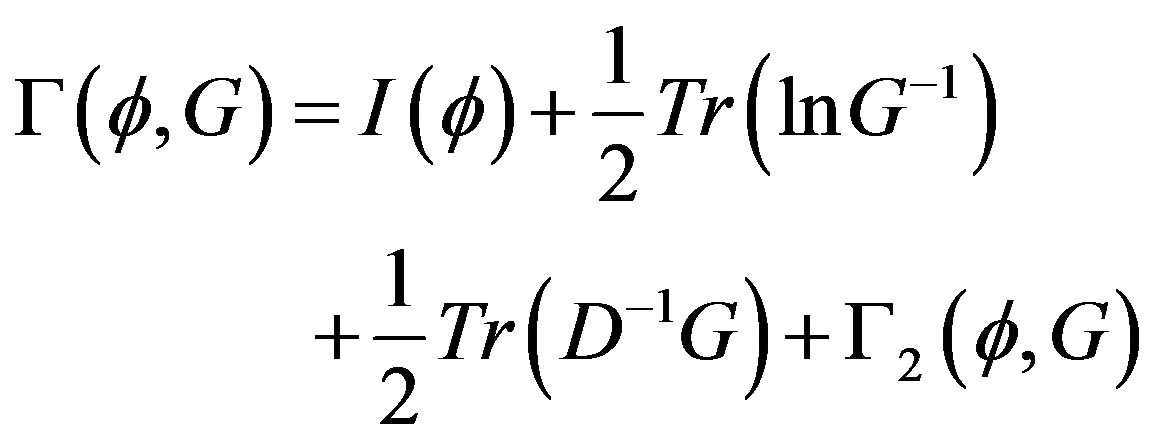 (39)
(39)
where in this last equation 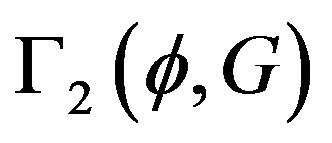 is the sum of all two-particle irreducible (2PI) diagrams in which all lines represent full (dressed) propagators
is the sum of all two-particle irreducible (2PI) diagrams in which all lines represent full (dressed) propagators , while
, while  is the inverse of the tree-level propagator. When translation invariance is not broken it is sufficient to consider a classical constant field configuration
is the inverse of the tree-level propagator. When translation invariance is not broken it is sufficient to consider a classical constant field configuration . Under this assumption we can factorize an overall four-dimensional volume factor and define the effective potential for composite operators
. Under this assumption we can factorize an overall four-dimensional volume factor and define the effective potential for composite operators 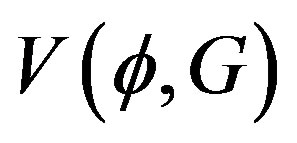 exactly as we did for the standard effective potential. Then the stationary condition are given by Equations (37) and (38) with
exactly as we did for the standard effective potential. Then the stationary condition are given by Equations (37) and (38) with 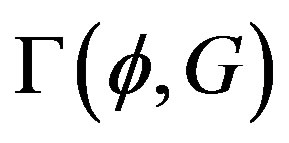 replaced by
replaced by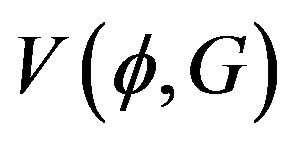 .
.

