Applied Mathematics
Vol.06 No.08(2015), Article ID:57741,5 pages
10.4236/am.2015.68108
On the Non-Common Neighbourhood Energy of Graphs
Ahmad N. Al-Kenani1, Anwar Alwardi2, Omar A. Al-Attas1
1Department of Mathematics, King Abdulaziz University, Jeddah, Saudi Arabia
2Department of Studies in Mathematics, University of Mysore, Mysore, India
Email: aalkenani10@hotmail.com, a_wardi@hotmail.com, Omar_alattas30@hotmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 May 2015; accepted 30 June 2015; published 3 July 2015
ABSTRACT
In this paper, we introduce a new type of graph energy called the non-common-neighborhood energy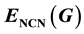 , NCN-energy for some standard graphs is obtained and an upper bound for
, NCN-energy for some standard graphs is obtained and an upper bound for 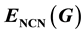 is found when G is a strongly regular graph. Also the relation between common neigh- bourhood energy and non-common neighbourhood energy of a graph is established.
is found when G is a strongly regular graph. Also the relation between common neigh- bourhood energy and non-common neighbourhood energy of a graph is established.
Keywords:
NCN-Eigenvalues (of Graph), NCN-Energy (of Graph), NCN-Adjacency Matrix (of Graph)

1. Introduction
Let G be a simple graph with n vertices, and let 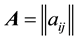 be its adjacency matrix. The eigenvalues
be its adjacency matrix. The eigenvalues 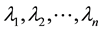 of
of 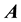 are the (ordinary) eigenvalues of the graph G [1] . Since
are the (ordinary) eigenvalues of the graph G [1] . Since 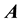 is a symmetric matrix with zero trace, these eigenvalues are real with sum equal to zero.
is a symmetric matrix with zero trace, these eigenvalues are real with sum equal to zero.
The energy of the graph G is defined [2] as the sum of the absolute values of its eigenvalues:
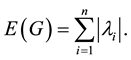
Details on the theory of graph energy can be found in the reviews [3] -[5] , whereas details on its chemical applications in the book [6] and in the review [7] . Let G be simple graph with vertex set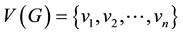 .
.
For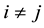 , the common neighborhood of the the vertices
, the common neighborhood of the the vertices 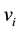 and
and , denoted by
, denoted by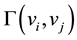 , is the set of
, is the set of
vertices, different from 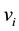 and
and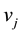 , which are adjacent to both
, which are adjacent to both 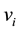 and
and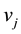 . The common-neighborhood matrix of G is then
. The common-neighborhood matrix of G is then
The common-neighborhood energy (or, shorter, CN-energy) of the graph G is
where 

Theorem 1. [8] For almost all n-vertex graphs
Theorem 1 immediately implies that almost all graphs are hyperenergetic, making any further search for them pointless.
In what follows we shall need a few auxiliary results.
Lemma 1. [1] Let G be a connected k-regular graph with n vertices and




Lemma 2. [1] Let G be a graph with an adjacency matrix A and with eigenvalues





Corollary 1. [9] Let G be a connected k-regular graph and let 
1) The common-neighborhood eigenvalues of the complement of G are
2) The common-neighborhood eigenvalues of the line graph 
where the CN-eigenvalue 

Definition. A strongly regular graph with parameters 


2. Non-Common Neighbourhood Energy of Graphs
Definition. Let G be simple graph with vertex set

borhood set of the the vertices 







According to the above definition, the non-common neighborhood matrix is a real symmetric 




Definition. The non-common neighborhood energy (or, shorter, CNC-energy) of the graph G is
We will Denote by 

Proposition 2.

Proof. Observing that

Proposition 3. 


Proof. First observe that if the vertices of 


Observing that 

Which implies
Corollary 2.
Proposition 4.


Proposition 5. For any totally disconnected graph

Proof. Observing that for any two vertices u and v in 

both vertices u and v. Therefore

complete graph with n vertices. Hence,
The complete multipartite graph 

partitioned into parts of cardinalities


the multipartite graph
Proposition 6. Let 


Proof. Let 

of complete multipartite graph we observe for any two distinct vertices 





where 

Corollary 3. For graph 
Corollary 4. For any cocktail party graph G which is the complement of
The proof of the following result is straightforward.
Proposition 7. If the graph G consists of (disconnected) components
Theorem 8. Let G be a graph on n vertices, and let 

and Let
Proof. Since 



Lemma 3. Let 

Then
Proof. Observing that if 

Therefore,
Hence
Proposition 9. For any k-regular graph G,
Proof. By Theorem 8 and Lemma 3, we have
Hence
Theorem 10. For any graph G,
Proof. Since 



equal to the number of vertices which adjacent to both 



Theorem 11. Let G be a connected k-regular graph with eigenvalues
of G are
Proof. Theorem 11 follows from Proposition 8 and Lemma 2 or by applying Theorem 10 and Corollary 1
Theorem 12. Let G be a connected k-regular graph and let 

Proof. Theorem 12 follows from Proposition 8 and Lemma 2 or by applying Theorem 10 and Corollary 1
Theorem 13. For any connected graph G, 




Proof. Let 









Conversely, if G is connected graph and
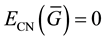


for some positive integer


Lemma 4. If G is a strongly regular graph with parameters

Proof. If 




tices of G, then


non-adjacent vertices,
from which Equation (1) follows straightforwardly.
Theorem 14. If G is a strongly regular graph with parameters

Proof. follows an idea first used by Koolen and Moulton [10] [11] . Let 


The Cauchy-Schwarz inequality states that if 

Now, by setting 


Therefore
i.e.,
i.e.,
By using Lemma 4,
Acknowledgements
We thank the Editor and the referee for their comments.
References
- Cvetković, D., Doob, M. and Sachs, H. (1995) Spectra of Graphs―Theory and Application. Barth, Heidelberg.
- Gutman, I. (1978) The Energy of a Graph. Ber. Math. Stat. Sekt. Forschungsz. Graz, 103, 1-22.
- Gutman, I. (2001) The Energy of a Graph: Old and New Results. In: Betten, A., Kohnert, A., Laue, R. and Wassermann, A., Eds., Algebraic Combinatorics and Applications, Springer-Verlag, Berlin, 196-211. http://dx.doi.org/10.1007/978-3-642-59448-9_13
- Gutman, I. (2011) Hyperenergetic and Hypoenergetic Graphs. In: Cvetković, D. and Gutman, I., Eds., Selected Topics on Applications of Graph Spectra, Math. Inst., Belgrade, 113-135.
- Gutman, I., Li, X. and Zhang, J. (2009) Graph Energy. In: Dehmer, M. and Emmert-Streib, F., Eds., Analysis of Complex Networks. From Biology to Linguistics, Wiley-VCH, Weinheim, 145-174. http://dx.doi.org/10.1002/9783527627981.ch7
- Gutman, I. and Polansky, O.E. (1986) Mathematical Concepts in Organic Chemistry. Springer-Verlag, Berlin. http://dx.doi.org/10.1007/978-3-642-70982-1
- Gutman, I. (2005) Topology and Stability of Conjugated Hydrocarbons. The Dependence of Total p-Electron Energy on Molecular Topology. Journal of the Serbian Chemical Society, 70, 441-456.
- Nikiforov, V. (2007) The Energy of Graphs and Matrices. Journal of Mathematical Analysis and Applications, 326, 1472-1475. http://dx.doi.org/10.1016/j.jmaa.2006.03.072
- Alwardi, A., Soner, N.D. and Gutman, I. (2011) On the Common-Neighborhood Energy of a Graph. Bulletin T. CXLIII de l’Académie Serbe des Sciences et des Arts 2011 Classe des Sciences Mathématiques et Naturelles Sciences Mathé- matiques, 143, 49-59.
- Koolen, J. and Moulton, V. (2001) Maximal Energy Graphs. Advances in Applied Mathematics, 26, 47-52. http://dx.doi.org/10.1006/aama.2000.0705
- Koolen, J.H., Moulton, V. and Gutman, I. (2000) Improving the McClelland Inequality for Total p-Electron Energy. Chemical Physics Letters, 320, 213-216. http://dx.doi.org/10.1016/S0009-2614(00)00232-3





































