Applied Mathematics
Vol.4 No.5(2013), Article ID:31223,5 pages DOI:10.4236/am.2013.45102
Least Squares Symmetrizable Solutions for a Class of Matrix Equations
School of Sciences, Institute of Mathematics and Physics, Central South University of Forestry and Technology, Changsha, China
Email: lfl302@tom.com
Copyright © 2013 Fanliang Li. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 30, 2013; revised March 27, 2013; accepted April 4, 2013
Keywords: Matrix Equations; Matrix Row Stacking; Topological Isomorphism; Least Squares Solution; Optimal Approximation
ABSTRACT
In this paper, we discuss least squares symmetrizable solutions of matrix equations (AX = B, XC = D) and its optimal approximation solution. With the matrix row stacking, Kronecker product and special relations between two linear subspaces are topological isomorphism, and we derive the general solutions of least squares problem. With the invariance of the Frobenius norm under orthogonal transformations, we obtain the unique solution of optimal approximation problem. In addition, we present an algorithm and numerical experiment to obtain the optimal approximation solution.
1. Introduction
The matrix equations (AX = B, XC = D), where A, B, C, D are usually given by experiments, have a long history [1]. Many authors considered these matrix equations. For example, Mitra [2,3], Chu [4] discussed its unconstraint solutions with the generalized inverse of matrix and the singular value decomposition (SVD), respectively. In recent years, many authors considered its constraint solutions. A series of meaningful results were achieved [1,5- 10]. The methods in these papers are mainly the generalized inverse of matrix and special properties of finite dimensional vector spaces [1,5,6], the decomposition of matrix or matrix pairs [7,8] and the special properties of constraint matrices [9,10]. However, the least squares symmetrizable solutions for these matrix equations have not been considered. The purpose of this paper is to discuss its least squares symmetrizable solutions with the matrix row stacking, Kronecker product and special relations between two linear subspaces which are topological isomorphism because the structure of symmetrizable matrices can not be found and the methods applied in [1-10] can not solve the problem in this paper. The background for introducing the definition of symmetrizable matrices is to get “symmetric” matrices from nonsymmetric matrices [11] because of nice properties and multi-areas of applications of symmetric matrices. For example, Sun [12] introduced the definition of positive definite symmetrizable matrices to study an efficient algorithm for solving the nonsymmetry second-order elliptic discrete systems.
Throughout this paper we use some notations as follows. Let  be the set of all
be the set of all ![]() real matrices and denote
real matrices and denote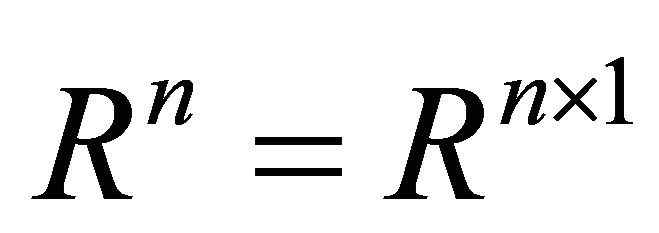 ;
;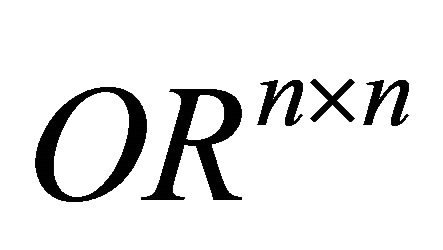 ,
, 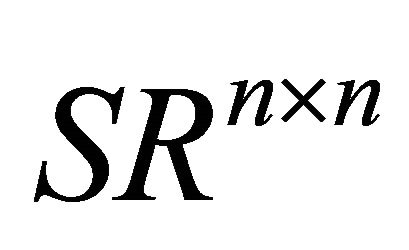 and
and 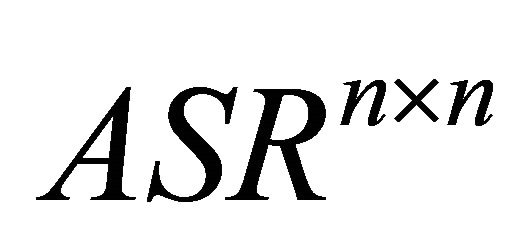 are the set of all
are the set of all ![]() orthogonal, symmetric and skewsymmetric matrices, respectively.
orthogonal, symmetric and skewsymmetric matrices, respectively.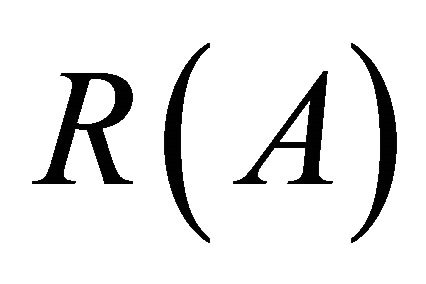 ,
,  and
and  represent the range, the transpose and the Moore-Penrose generalized inverse of A, respectively.
represent the range, the transpose and the Moore-Penrose generalized inverse of A, respectively.
In denotes the identity matrix of order n. For ,
, 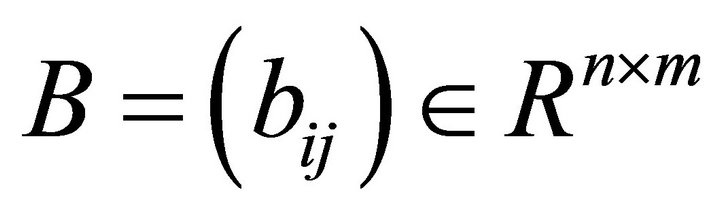 ,
, 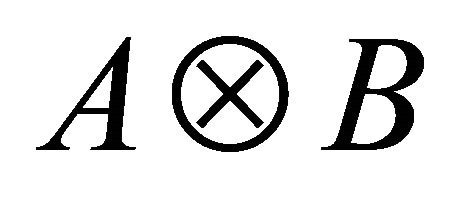 denotes Kronecker product of matrix A and B;
denotes Kronecker product of matrix A and B; 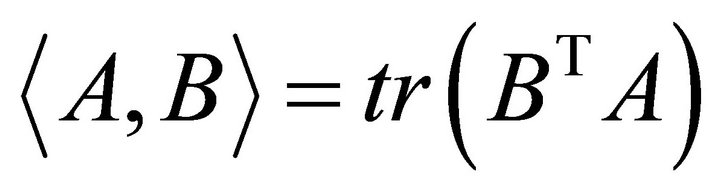 denotes the inner product of matrix A and B. The induced matrix norm is called Frobenius norm, i.e.
denotes the inner product of matrix A and B. The induced matrix norm is called Frobenius norm, i.e.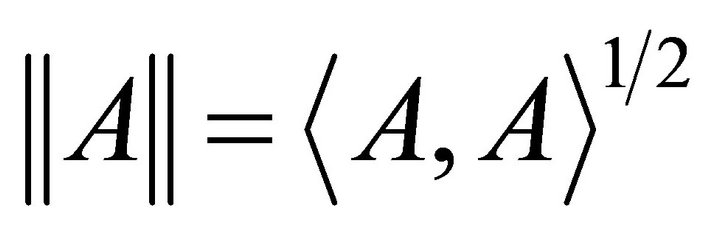 , then
, then  is a Hilbert inner product space.
is a Hilbert inner product space.
Definition 1. A real ![]() matrix A is called a symmetrizable (skew-symmetrizable) matrix if A is similar to a symmetric (skew-symmetric) matrix A. The set of symmetrizable (skew-symmetrizable) matrices is denoted by
matrix A is called a symmetrizable (skew-symmetrizable) matrix if A is similar to a symmetric (skew-symmetric) matrix A. The set of symmetrizable (skew-symmetrizable) matrices is denoted by 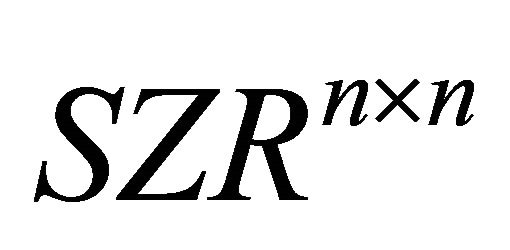
 .
.
From Definition 1, it is easy to prove that 
 if and only if there exists a nonsingular matrix W and a symmetric (skew-symmetric) matrix
if and only if there exists a nonsingular matrix W and a symmetric (skew-symmetric) matrix  such that
such that
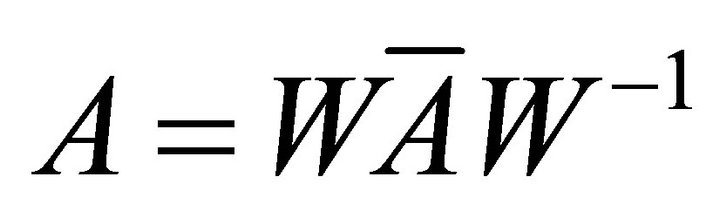
We now introduce the following two special classes of subspaces in![]() .
.
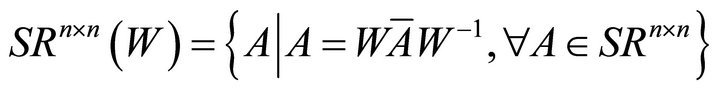 ,
,
 .
.
It is easy to see that if W is a given nonsingular matrix, then 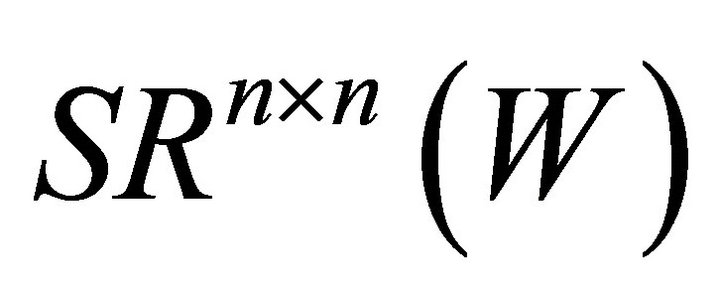 and
and 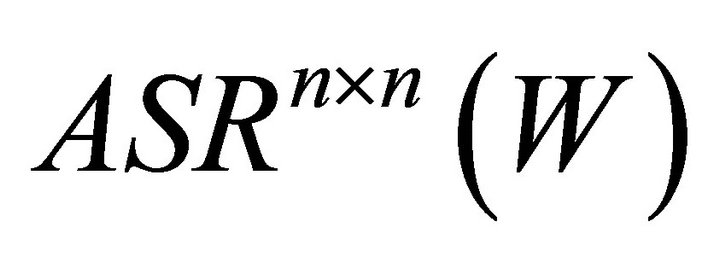 are two closed linear subspace of
are two closed linear subspace of![]() . In this paper, we suppose that W is a given nonsingular matrix and
. In this paper, we suppose that W is a given nonsingular matrix and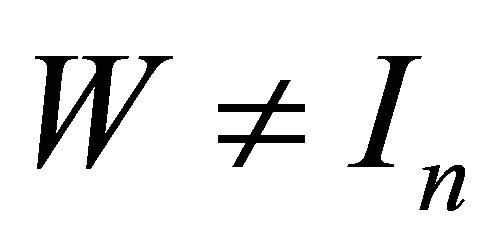 . We will consider the following problems.
. We will consider the following problems.
Problem I. Giving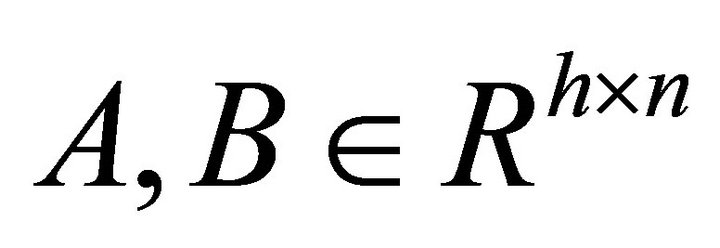 ,
,  , find
, find 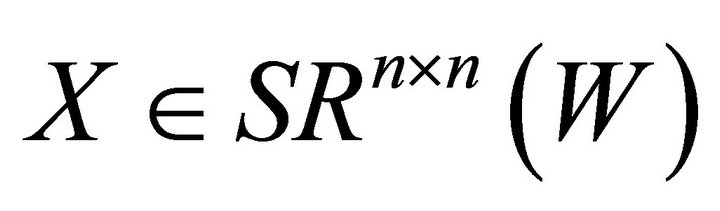 such that
such that
 .
.
Problem II. Given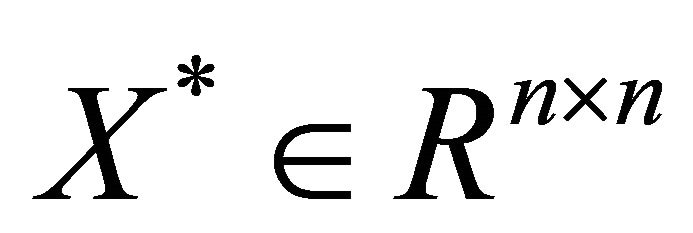 , find
, find 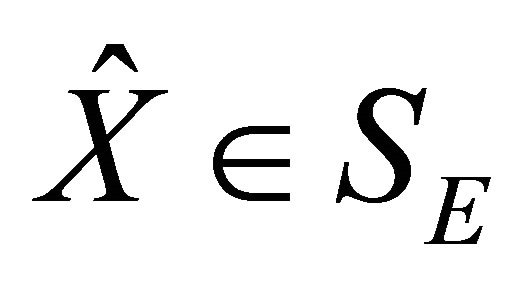 such that
such that
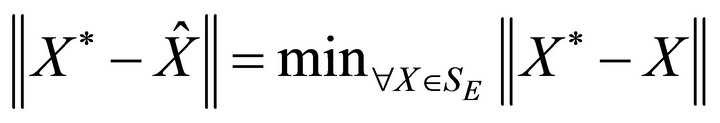 where
where 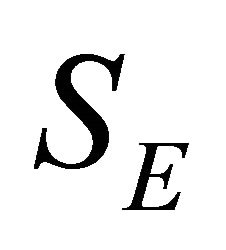 is the solution set of Problem I.
is the solution set of Problem I.
In this paper, if C = 0, D = 0 in Problem I, then Problem I becomes Problem I of [13]. Peng [13] studied the least squares symmetrizable solutions of the matrix equation AX = B with the singular value decomposition of matrix. The method applied in [13] can not solve Problem I in this paper. In this paper, we first take matrix equations (AX = B, XC = D) into linear equations with matrix row stacking and Kronecker product. Then we obtain an orthogonal basis-set for  with special relations between two linear subspaces which are topological isomorphism. Based on these results, we obtain the general expression of Problem I.
with special relations between two linear subspaces which are topological isomorphism. Based on these results, we obtain the general expression of Problem I.
This paper is organized as follows. In Section 2, we first discuss the matrix row stacking methods, Kronecker product of matrix and relations between 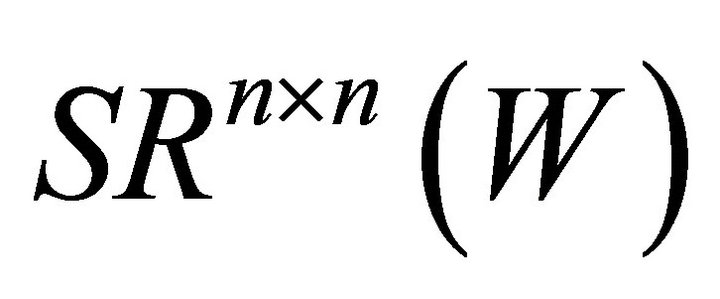 and
and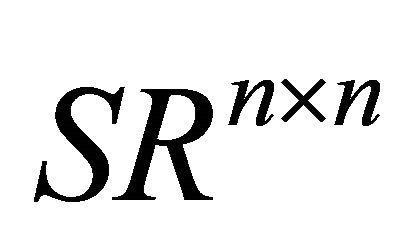 . Then we obtain the general solutions of Problem I. In Section 3, we derive the solution of Problem II with the invariance of Frobenius norm under orthogonal transformations. In the end, we give an algorithm and numerical experiment to obtain the optimal approximation solution.
. Then we obtain the general solutions of Problem I. In Section 3, we derive the solution of Problem II with the invariance of Frobenius norm under orthogonal transformations. In the end, we give an algorithm and numerical experiment to obtain the optimal approximation solution.
2. The Solution Set of Problem I
At first, we discuss the matrix row stacking methods, Kronecker product of matrix and relations between two linear subspaces which are topological isomorphism.
For any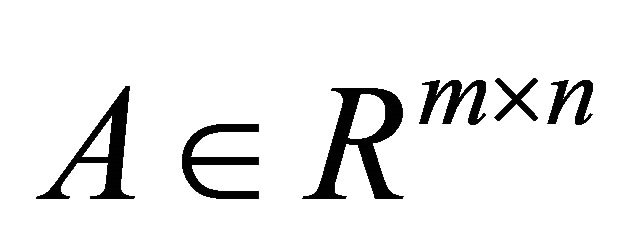 , let
, let 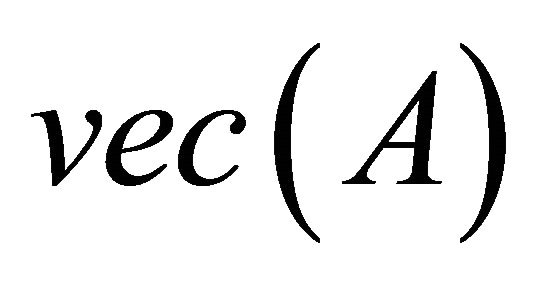 denote an ordered stack of the row of A from upper to low stacking with the first row, i.e.
denote an ordered stack of the row of A from upper to low stacking with the first row, i.e.
 , (2.1)
, (2.1)
where 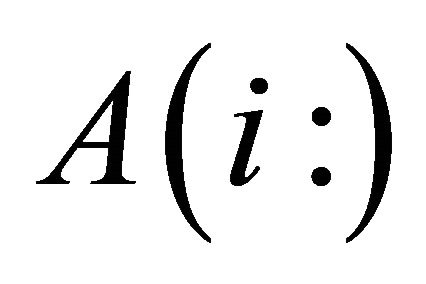 denotes the ith row of A. For any vector
denotes the ith row of A. For any vector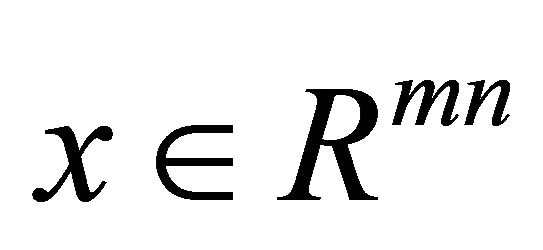 , let
, let 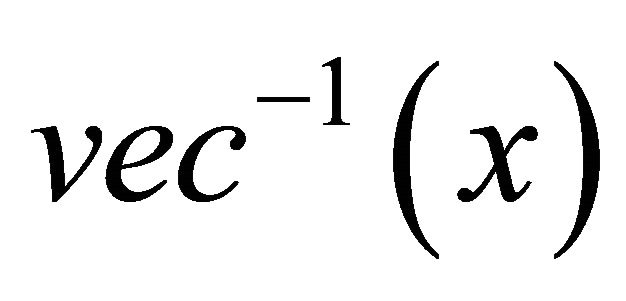 denote the following matrix containing all the entries of vector x.
denote the following matrix containing all the entries of vector x.
 , (2.2)
, (2.2)
where  denotes the elements from i to j of vector
denotes the elements from i to j of vector![]() . From (2.1), we can derive the following two linear subspaces of
. From (2.1), we can derive the following two linear subspaces of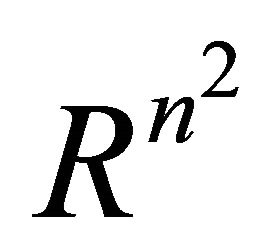 .
.
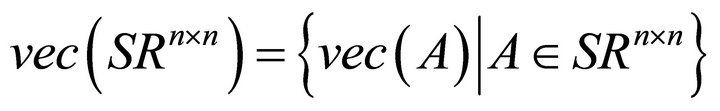 , (2.3)
, (2.3)
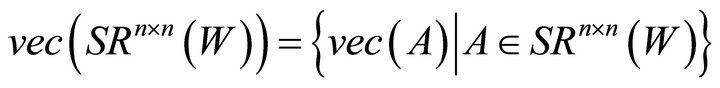 .
.
Lemma 1. [14] If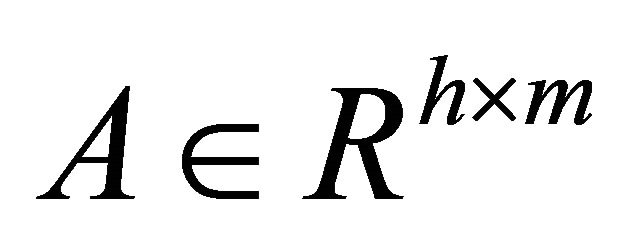 ,
, 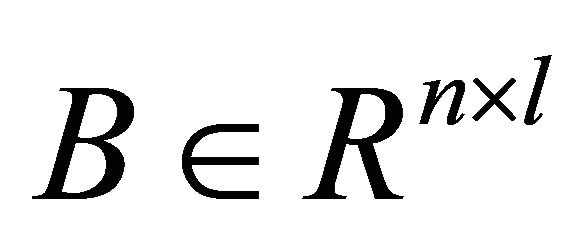 ,
,  , then
, then
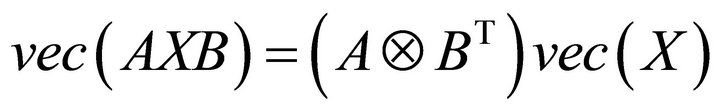 . (2.4)
. (2.4)
For any , let
, let
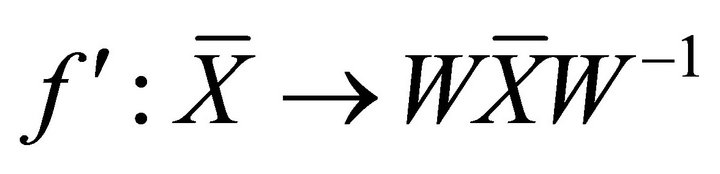 , i.e.
, i.e.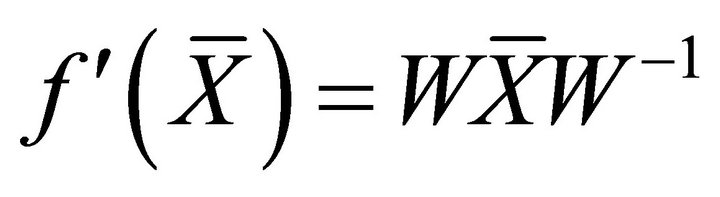 . (2.5)
. (2.5)
It is no difficult to prove that mapping  is a topological isomorphism mapping from
is a topological isomorphism mapping from 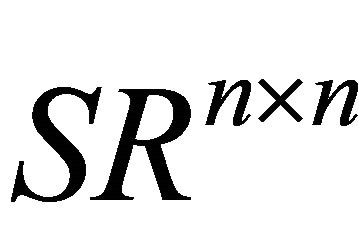 to
to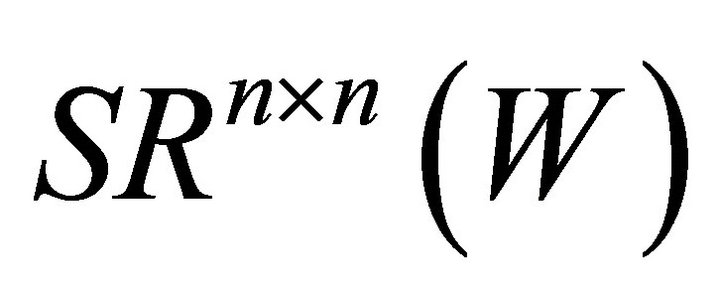 . According to (2.1) and (2.5), it is easy to derive the following mapping from linear subspaces
. According to (2.1) and (2.5), it is easy to derive the following mapping from linear subspaces 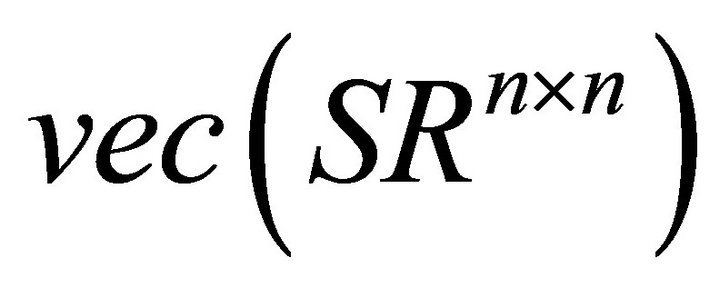 to
to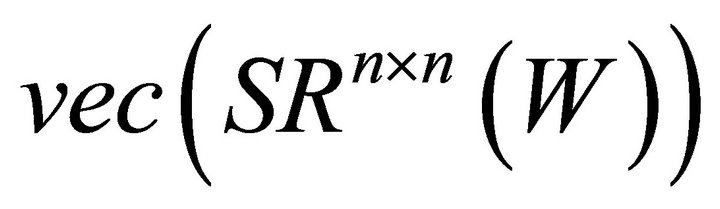 .
.
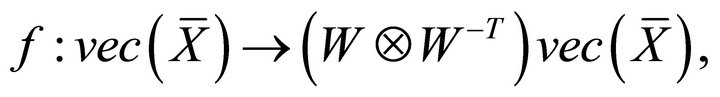
i.e.
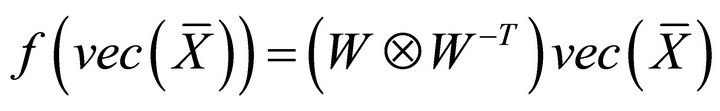 (2.6)
(2.6)
It is also easy to prove that mapping 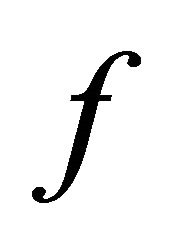 is a topological isomorphism mapping from
is a topological isomorphism mapping from 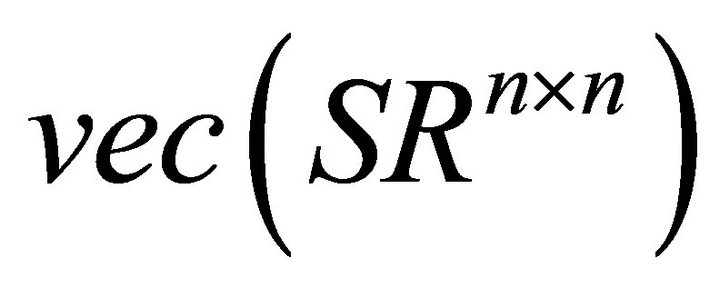 to
to
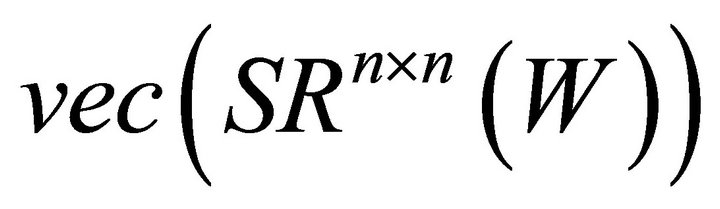 . It is clear that the dimension of
. It is clear that the dimension of 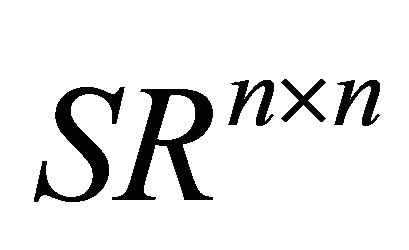
is . This implies that the dimension of
. This implies that the dimension of 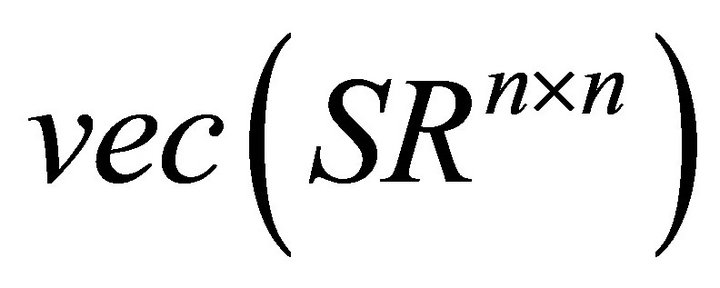 and
and 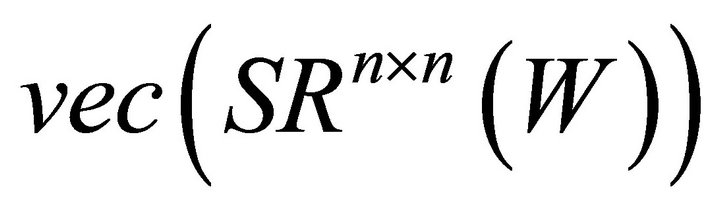 are also
are also . In this paper, let
. In this paper, let .
.
Lemma 2. If 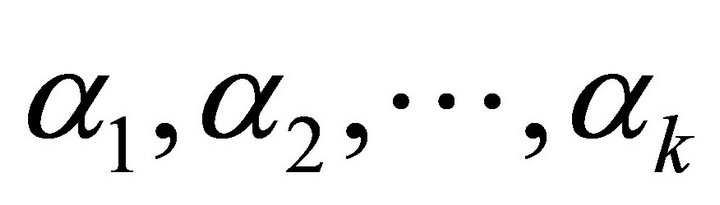 is an orthonormal basisset for
is an orthonormal basisset for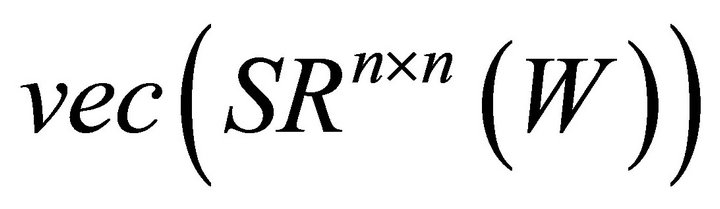 , and let
, and let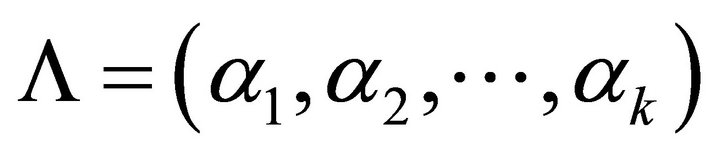 , then the following relations hold.
, then the following relations hold.
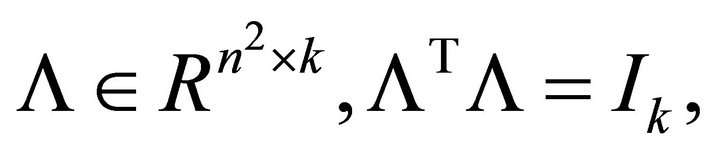 (2.7)
(2.7)

From the definition of the orthonormal basis-set, it is easy to prove Lemma 2, so the proof is omitted.
For any matrix , if let
, if let 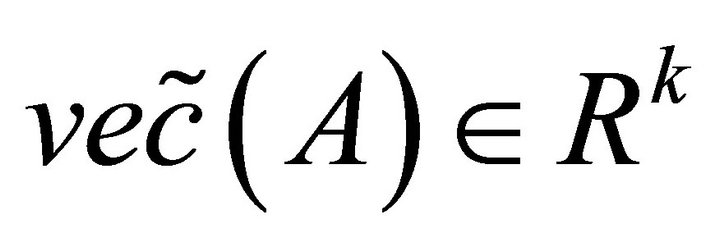 denote the vector of coordinates of
denote the vector of coordinates of 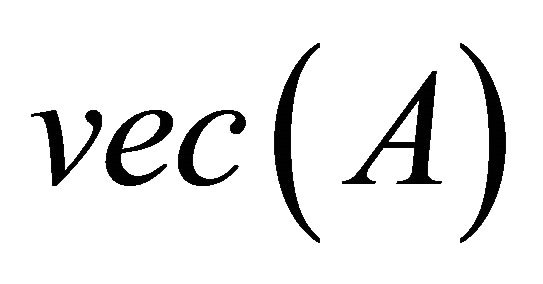 with respect to the basis-set
with respect to the basis-set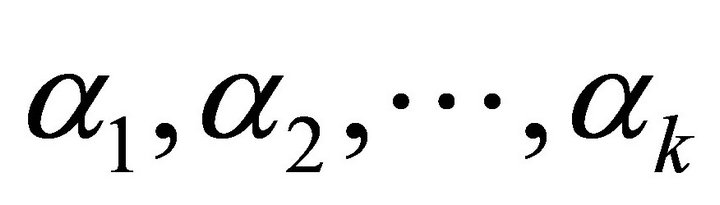 , then combining (2.4) and (2.7), we have
, then combining (2.4) and (2.7), we have
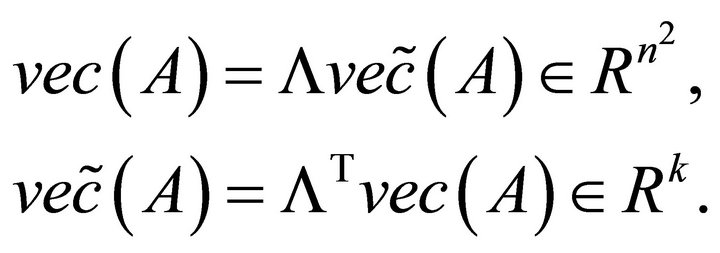 (2.8)
(2.8)
Moreover, for any , the following conclusion holds.
, the following conclusion holds.
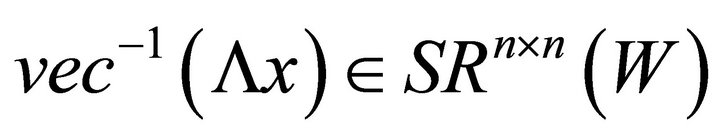 . (2.9)
. (2.9)
The orthonormal basis-set  for
for  can be obtained by the following calculation procedure.
can be obtained by the following calculation procedure.
Calculation procedure
Step 1. Input a basis-set 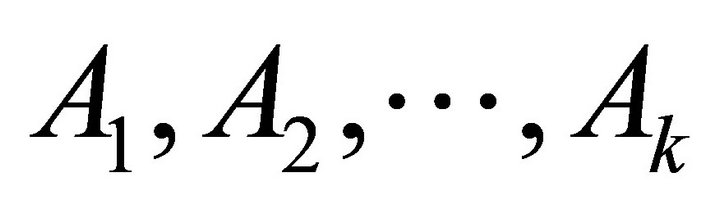 for
for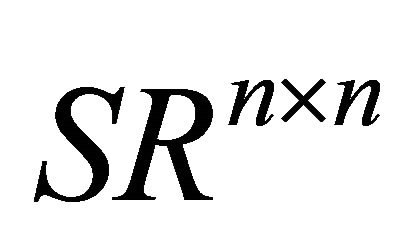 .
.
Step 2. According to (2.1), compute 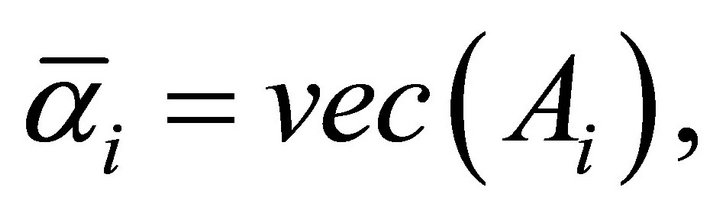
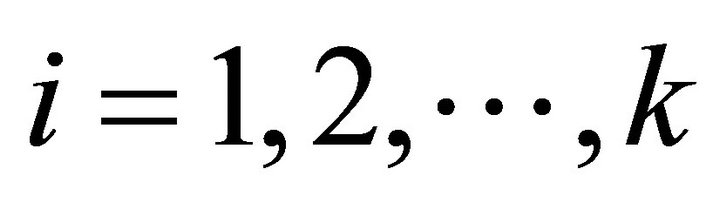 , and obtain a basis-set
, and obtain a basis-set 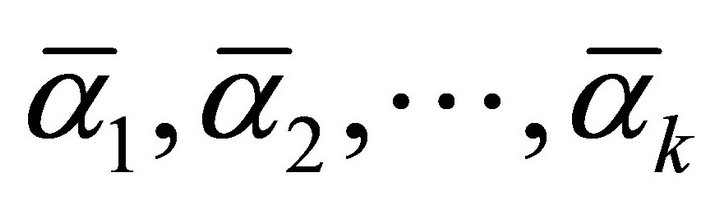 for
for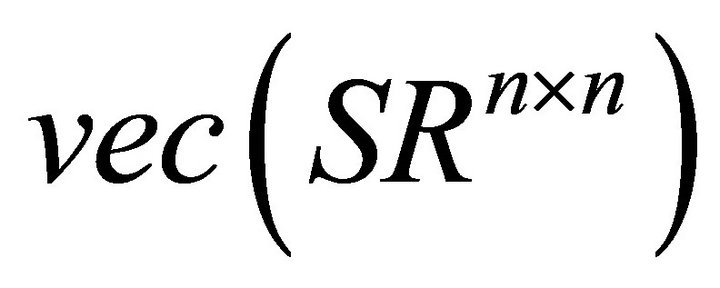 .
.
Step 3. Input a nonsingular matrix W, compute
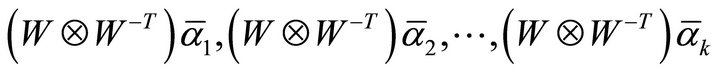 and obtain a basis-set for
and obtain a basis-set for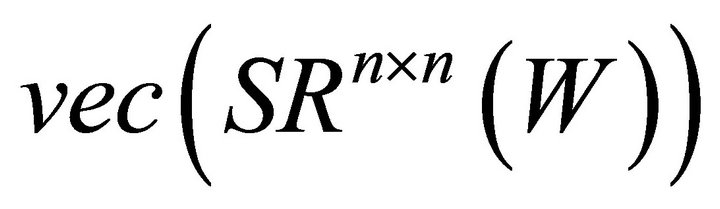 .
.
Step 4. Compute the QR decomposition of matrix
 and obtain an orthonormal basis-set
and obtain an orthonormal basis-set 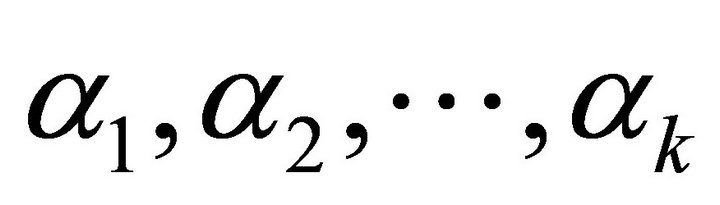 for
for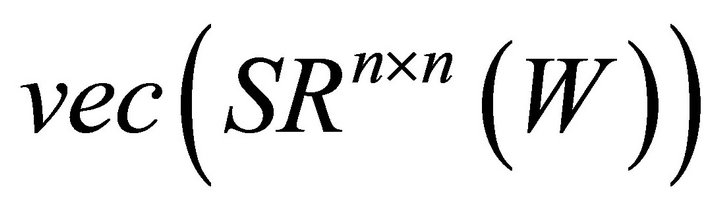 .
.
Lemma 3. If ,
, 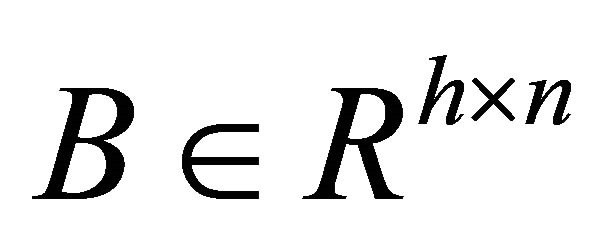 , then the general solutions of least squares problem
, then the general solutions of least squares problem

is
 .
.
With the singular value decomposition of matrix, it is easy to prove this lemma. So the proof is omitted.
Theorem 1. Giving ,
,  , and let
, and let
 , (2.11)
, (2.11)
then the general solutions of Problem I is
 (2.12)
(2.12)
Proof. From Lemma 1, we have
This implies that finding  such that
such that  if and only if finding
if and only if finding  such that
such that
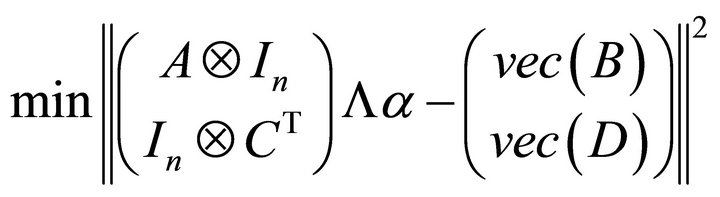 , (2.13)
, (2.13)
where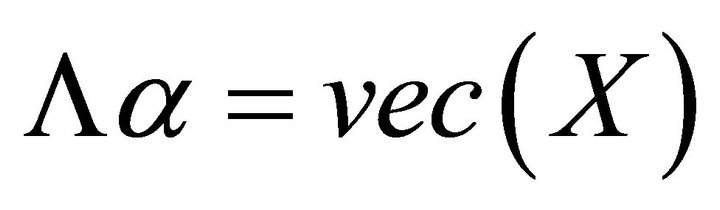 . From Lemma 3, the general solutions of (2.13) is
. From Lemma 3, the general solutions of (2.13) is
 (2.14)
(2.14)
Combining (2.13) and (2.14) gives (2.12). □
3. The Solution of Problem II
Let  be the solution set of Problem I. From (2.12), it is easy to see that
be the solution set of Problem I. From (2.12), it is easy to see that  is a nonempty closed convex set. So we claim that for any given
is a nonempty closed convex set. So we claim that for any given , there exists the unique optimal approximation for Problem II.
, there exists the unique optimal approximation for Problem II.
Theorem 2. If given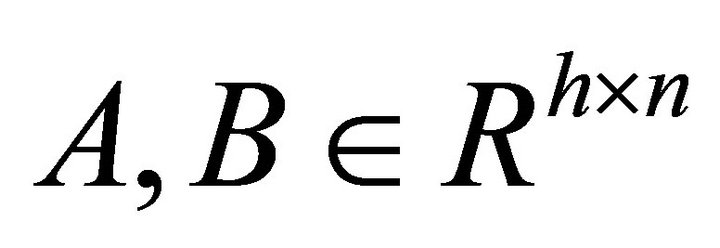 ,
,  ,
, ![]()
 , then Problem II has a unique solution
, then Problem II has a unique solution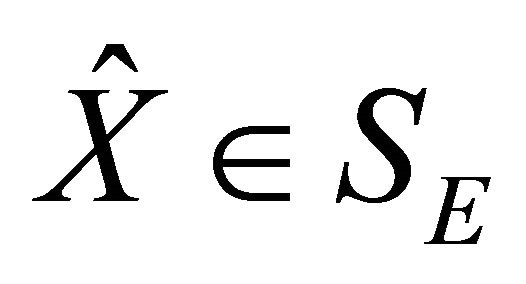 . Moreover,
. Moreover, 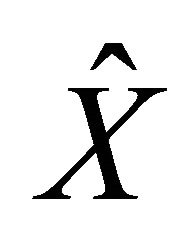 can be expressed as
can be expressed as
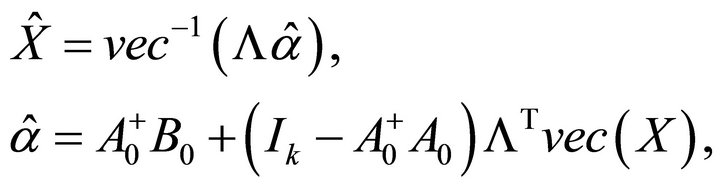 (3.1)
(3.1)
where 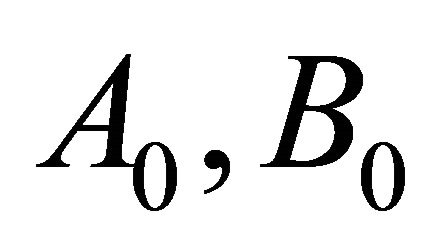 are denoted by (2.11).
are denoted by (2.11).
Proof. Choose  such that
such that![]() . Combining the invariance of the Frobenius norm under orthogonal transformations, (2.12) and (2.14), we have
. Combining the invariance of the Frobenius norm under orthogonal transformations, (2.12) and (2.14), we have

Let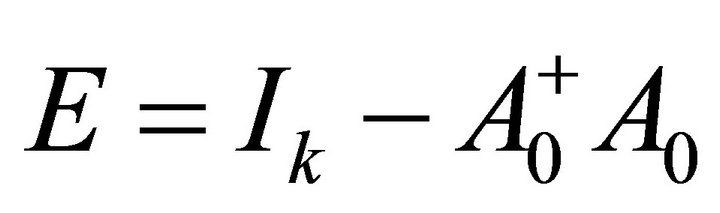 ,
, 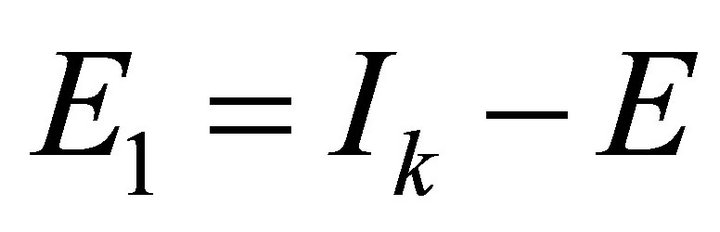 , it is clear that
, it is clear that  are orthogonal projection matrices satisfying
are orthogonal projection matrices satisfying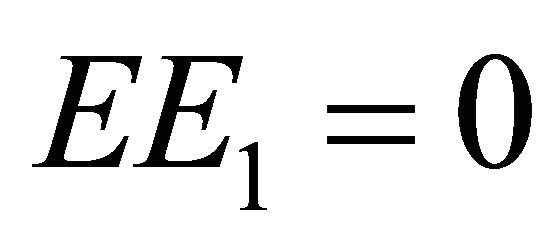 . Hence, we have
. Hence, we have

It is easy to prove that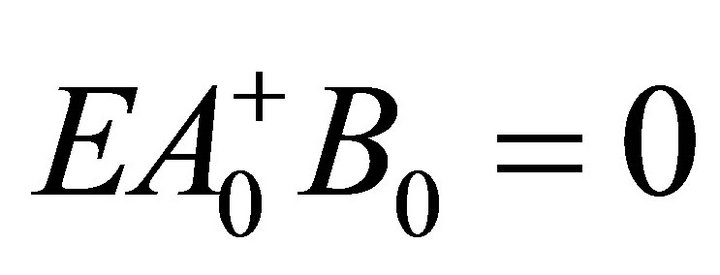 . This implies that
. This implies that
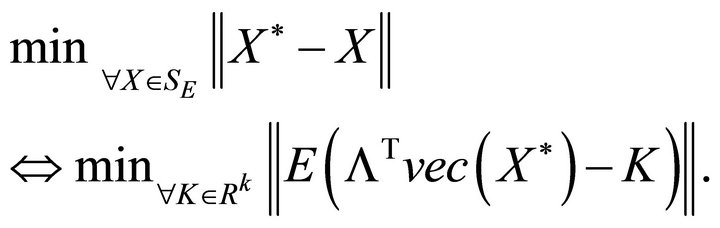 (3.2)
(3.2)
The solution of (3.2) is
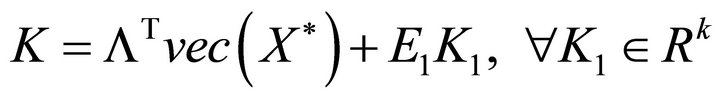 . (3.3)
. (3.3)
Substituting (3.3) to (2.12) gives (3.1). □
From Theorem 2, we can design the following algorithm to obtain the optimal approximate solution.
Algorithm
1) Input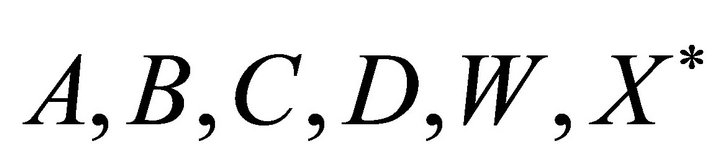 .
.
2) Input a basis-set 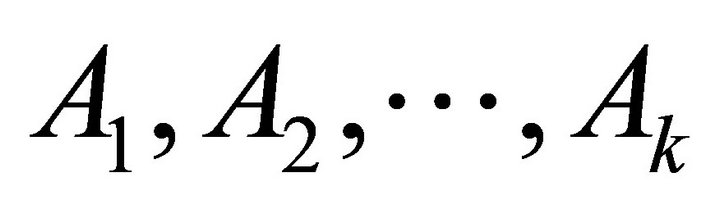 for
for .
.
3) According to the calculation procedure before, compute 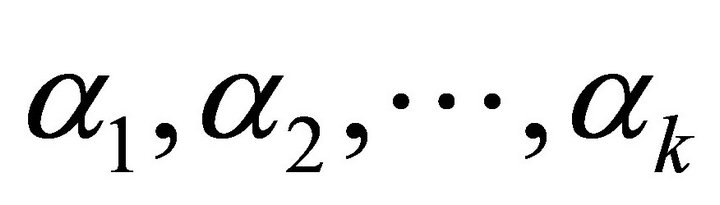 and obtain an orthonormal basis-set for
and obtain an orthonormal basis-set for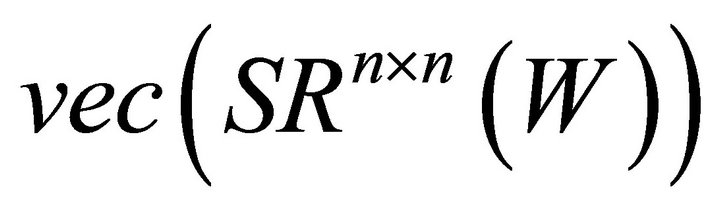 .
.
4) Let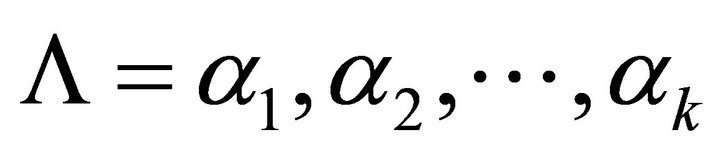 , compute A0, B0 from (2.11).
, compute A0, B0 from (2.11).
5) Compute  from the second equation of (3.1).
from the second equation of (3.1).
6) According to the first equation of (3.1), calculate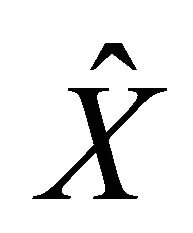 .
.
Example 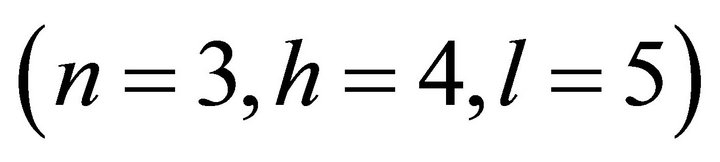
1) Input  as follows.
as follows.
 ,
,
 ,
,
 ,
,
 ,
,
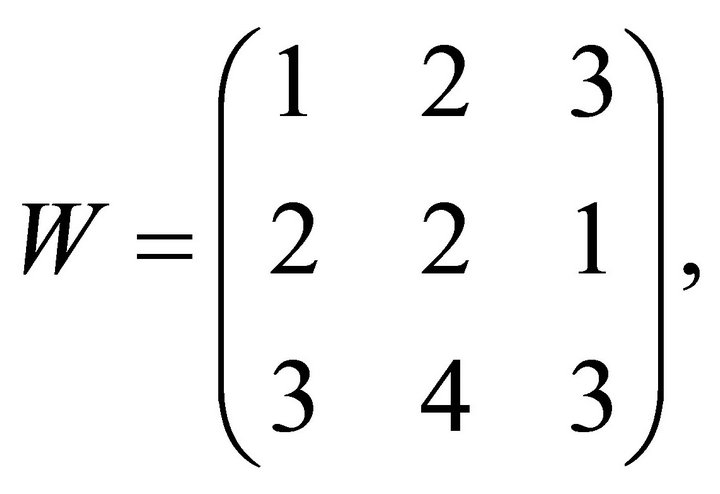
 .
.
2) Input a basis-set 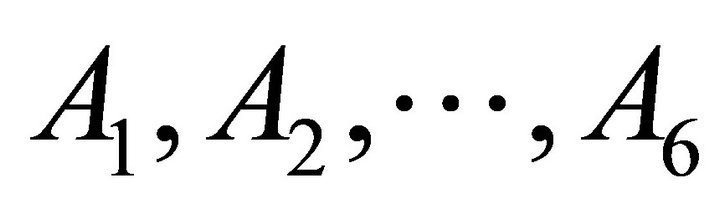 for
for 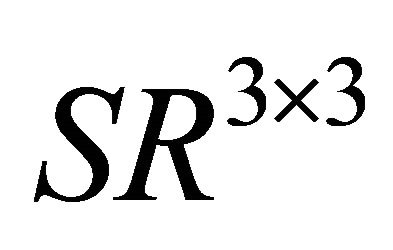 as follows.
as follows.
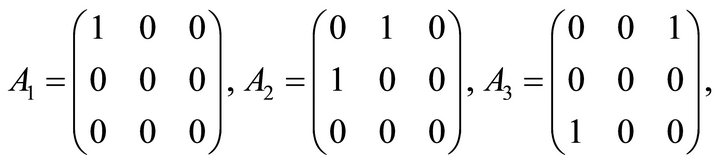
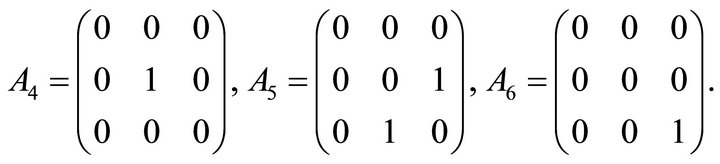
3) According to the calculation procedure, we obtain an orthonormal basis-set 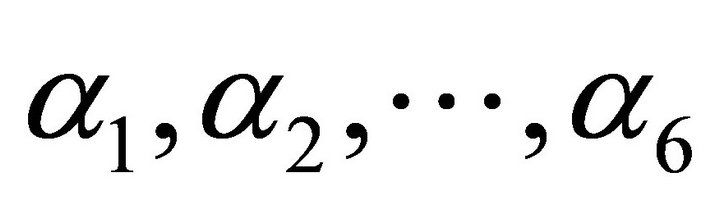 for
for
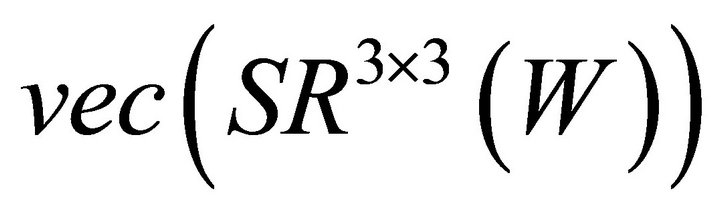 as follows.
as follows.


4) Using the software “MATLAB”, we obtain the unique solution 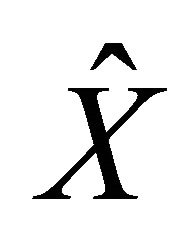 of Problem II.
of Problem II.
 .
.
4. Conclusion
In this paper, we first derive the least squares symmetrizable solutions of matrix equations (AX = B, XC = D) with the matrix row stacking and the theory of topological isomorphism, i.e. Theorem 1. Then we give the unique optimal approximation solution, i.e. Theorem 2. Based on Theorem 1 and 2, we design an algorithm to find the optimal approximation solution. Compare to [1-10], this paper has two important achievements. One is we apply the topological isomorphism theory to obtain the least squares symmetrizable solutions of matrix equations (AX = B, XC = D), and provide a method to solve the matrix equation, where the construct of constraint matrix can not be found. The other is we present a stable calculation procedure to obtain an orthonormal basis-set for 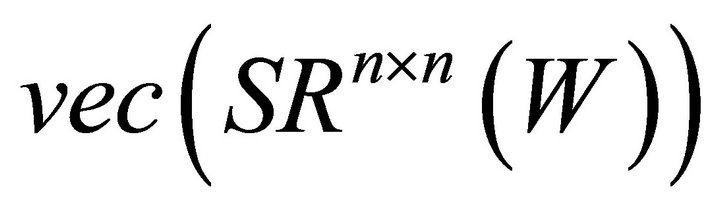 , and solve the key problem of the algorithm.
, and solve the key problem of the algorithm.
5. Acknowledgements
The authors are very grateful to the referee for their valuable comments, and also thank for his helpful suggestions.
This research was supported by National natural Science Foundation of China (31170532).
REFERENCES
- A. Dajić and J. J. Koliha, “Equations ax = c and xb = b in Rings and Rings with Involution with Applications to Hilbert Space Operators,” Linear Algebra and Its Applications, Vol. 429, No. 7, 2008, pp. 1779-1809. doi:10.1016/j.laa.2008.05.012
- S. K. Mitra, “The Matrix Equations AX = C, XB = D,” Linear Algebra and Its Applications, Vol. 59, 1984, pp. 171-181. doi:10.1016/0024-3795(84)90166-6
- K. W. E. Chu, “Singular Value and Generalized Singular Value Decomposition and the Solution of Linear Matrix Equations,” Linear Algebra and Its Applications, Vol. 88-89, 1987, pp. 83-98. doi:10.1016/0024-3795(87)90104-2
- S. K. Mitra, “A Pair of Simultaneous Linear Matrix Equations A1XB1 = C1, A2XB2 = C2 and a Matrix Programming Problem,” Linear Algebra and Its Applications, Vol. 131, 1990, pp. 107-123. doi:10.1016/0024-3795(90)90377-O
- A. Dajić and J. J. Koliha, “Positive Solutions to the Equations AX = C, and XB = D for Hilbert Space Operators,” Journal of Mathematical Analysis and Applications, Vol. 333, No. 2, 2007, pp. 567-576. doi:10.1016/j.jmaa.2006.11.016
- Q. X. Xu, “Common Hermitian and Positive Solutions to the Adjointable Operator Equations AX = C, XB = D,” Linear Algebra and Its Applications, Vol. 429, No. 1, 2008, pp. 1-11. doi:10.1016/j.laa.2008.01.030
- Q. W. Wang, “Bisymmetric and Centrosymmetric Solutions to Systems of Real Quaternion Matrix Equations,” Computers and Mathematics with Applications, Vol. 49, No. 5-6, 2005, pp. 641-650. doi:10.1016/j.camwa.2005.01.014
- Y. Qiu and A. Wang, “Least Squares Solutions to the Equations AX = B, XC = D with Some Constraints,” Applied Mathematics and Computation, Vol. 204, No. 2, 2008, pp. 872-880. doi:10.1016/j.amc.2008.07.035
- F. L. Li, X. Y. Hu and L. Zhang, “The Generalized Reflexive Solution for a Class of Matrix Equations (AX = B, XC = D),” Acta Mathematica Scientia Series B, Vol. 1, No. 28, 2008, pp. 185-193.
- F. L. Li, X. Y. Hu and L. Zhang, “The Generalized Anti-Reflexive Solution for a Class of Matrix Equations (BX = C, XD = E),” Computational & Applied Mathematics, Vol. 1, No. 27, 2008, pp. 31-46.
- O. Taussky, “The Role of Symmetric Matrices in the Study of General Matrices,” Linear Algebra and Its Applications, Vol. 51, 1972, pp. 13-18.
- S. J. Chang, “On Positive Symmetrizable Matrices and Pre-Symmetry Iteration Algorithms,” Mathematica Numerica Sinica, Vol. 3, No. 22, 2000, pp. 379-384.
- Z. Y. Peng, “The Least-Squares Solution of Inverse Problem for One Kind of Symmetrizable Matrices,” Chinese Journal of Numerical Mathematics and Applications, No. 3, 2004, pp. 219-224.
- D. W. Fausett and C. T. Fulton, “Large Least Squares Problems Involving Kronecker Products,” SIAM Journal on Matrix Analysis and Applications, Vol. 15, No. 1, 1994, pp. 219-227. doi:10.1137/S0895479891222106

