Received 6 November 2014; revised 3 December 2014; accepted 9 December 2014

ABSTRACT

We proposed a kind of doubly periodic Riemann boundary value problem on two parallel curves. By using the method of complex functions, we investigated the method for solving this kind of dou- bly periodic Riemann boundary value problem of normal type and gave the general solutions and the solvable conditions for it.

Keywords:

Normal Type, Doubly Periodic, Riemann Boundary Problem

1. Introduction

Various kinds of Riemann boundary value problems (BVPs) for analytic functions on closed curves or on open arcs, doubly periodic Riemann BVPs, doubly periodic or quasi-periodic Riemann BVPs and Dirichlet Problems, and BVPs for polyanalytic functions have been widely investigated in papers [1] -[8] . The main approach is to use the decomposition of polyanalytic functions and their generalization to transform the boundary value problems to their corresponding boundary value problems for analytic functions. Recently, inverse Riemann BVPs for generalized analytic functions or bianalytic functions have been investigated in papers [9] - [13] .

In this paper, we consider a kind of doubly periodic Riemann boundary value problem on two parallel curves. By using the method of complex functions, we investigate the method for solving kind of doubly periodic Riemann boundary value problem of normal type and give the general solutions and the solvable conditions for it.

2. A Kind of Doubly Periodic Riemann Boundary Value Problem on Two Parallel Curves

Suppose that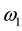, 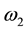are complex constants with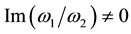, and P denotes the fundamental period parallelogram with vertices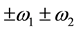. The function

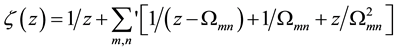
is called the Weierstrass 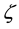-function, where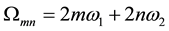, and 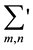denotes the sum for all m,

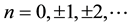, except for.

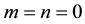Let 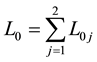be the set of two parallel curves, lying entirely in the fundamental period parallelogram P,

not passing the origin, with endpoints being periodic congruent and having the same tangent lines at the periodic congruent points. Let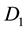, , 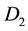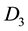denote the domains entirely in the fundamental period parallelogram P, cut by 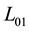and, respectively. Without loss of generality, we suppose that see Figure 1. Let, be the curves periodically extended for and with period, respectively. And be the curves periodically extended for with.

Our objective is to find sectionally holomorphic doubly periodic functions and, satisfying the following boundary conditions

(1)

where, , and be doubly periodic with. are the boundary values of the

function, which is analytic in and, belonging to the class on, satisfying the boun-

dary conditions (1), and are the boundary values of the function, which is analytic in, belonging to the class on, satisfying the boundary conditions (1).

Since plays the same roles as other points on , it is natural to require that the unknown functions are bounded at, that is, the unknown functions and are both bounded on and.

Problem (1) is called the normal type if, otherwise the non-normal type. And if we allow the solution has poles of order m at z = 0, it is actually to solve problem (1) in DR_m.

3. Preliminary Notes

Since with, by taking logarithm of for some branch on, we may obtain a continuous single-valued function such as

with. Now we call the integer the index of problem (1), where is the integer satisfying

.

Since can only be 0 and, the index can only take.

Set

(2)

(3)

We can easily see that will have singularities at most less than one order near the endpoints and. Let

(4)

then we have

, ,

where and. Thus is not doubly periodic generally. In fact, is doubly periodic if and only if

, is positive integer for. (5)

Lemma 1. Formula (5) is valid if and only if

,.

And if both and are true, then we have and, where, are all integers.

4. Solution for Problem (1) of Normal Type

Problem (1) can be transferred by using (3) as

(6)

Multiplying to the two sides of the first identity in equations (6), and multiplying to the two

sides of the second identity in Equations (6), gives

(7)

The function always has singularities at most less than one order near the endpoints and

whatever. And then, , must belong to class H or class

H^* on L₀₁ and L₀₂, respectively.

Case 1. If formula (5) holds, that is, is doubly periodic, then by Lemma 1 we have

. (8)

Let

(9)

(10)

Then by formulas (9) and (10), we may rewrite (7) as

(11)

Now we introduce the function

then has -order at z = 0, and has singularities at most less than one order near the endpoints a_j and. Thus we can get the following results.

When m > 0, problem (1) is solvable without any restrictive conditions and the general solution is given by

(12)

where are arbitrary constants.

When m = 0, problem (1) is solvable if and only if the restrictive conditions

(13)

are satisfied, and now the solution is given by

(14)

where is arbitrary constant.

When m < 0, if and only if the restrictive conditions (13) and

(15)

(when, the condition (15) is unnecessary) are necessary, problem (1) is solvable and the solution can still be given by (14) but with

,

Case 2. If formula (5) fails to hold, then by Lemma 1 we see that. Let

,

then the function become doubly periodic, and function has singularities at most less

than one order near the endpoints and. Thus now, we can transform (6) to

(16)

where, belong to class H or class H^* on L₀₁ and L₀₂, respectively. Write

(17)

(18)

By (17) and (18), we can rewrite (16) as

(19)

Now we will meet two kinds of situations in solving problem (1) in DR_m.

(a) When, the function is an entire function. And we can write it without counting nonzero constant as

,

where are determined by the identity.

When m > 0, problem (1) is solvable without any restrictive conditions and the general solution is given by

(20)

where are arbitrary constants.

When, problem (1) is solvable if and only if the restrictive conditions

(21)

are satisfied, and the general solution for (1) is given by

(22)

where is arbitrary constant.

When m < 0, if and only if the restrictive conditions (21) and

(23)

(when, the condition (23) is unnecessary) are both necessary, problem (1) is solvable and the solution can still be given by (22) but with

.

(b) When fails to hold, the function has singularity of one order at z = 0,

has singularities at most less than one order near the endpoints and, and has a zero of order one at. Write

(24)

then must be at most m + 1 ordered at z = 0, and has singularities less than one order at z = a_j (j = 1, 2).

When, problem (1) is solvable without any restrictive conditions and the general solution is given by

(25)

with the restrictive condition that

,

or

,

where are arbitrary constants, which is to ensure that, that is, to ensure and be bounded.

When, problem (1) is solvable if and only if the restrictive conditions

(26)

are satisfied, and now the solution is given by

(27)

which is finite at owing to its structure.

When, problem (1) is solvable if and only if both conditions (26) and the following conditions

(28)

(29)

(when, (28) is unnecessary) are necessary, and the solution is given by

(30)

which is finite at owing to its structure.

Funding

The project of this thesis is supported by “Heilongjiang Province Education Department Natural Science Research Item”, China (12541089).

References