Advances in Pure Mathematics
Vol.3 No.7(2013), Article ID:38113,6 pages DOI:10.4236/apm.2013.37078
On Some Integral Inequalities of Hardy-Type Operators
Department of Mathematics, University of Ilorin, Ilorin, Nigeria
Email: krauf@unilorin.edu.ng, omolehin_joseph@yahoo.com, sanusiakm@gmail.com
Copyright © 2013 Rauf Kamilu et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 12, 2013; revised May 15, 2013; accepted June 18, 2013
Keywords: Hardy’s Inequality; Measurable; Weight Functions & Hardy-Type Operators
ABSTRACT
In recent time, hardy integral inequalities have received attentions of many researchers. The aim of this paper is to obtain new integral inequalities of hardy-type which complement some recent results.
1. Introduction
The classical hardy integral inequality reads:
Theorem 1 Let 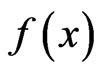 be a non-negative p-integrable function defined on
be a non-negative p-integrable function defined on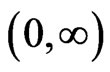 , and
, and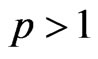 . Then,
. Then,  is integrable over the interval
is integrable over the interval 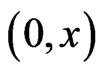 for each
for each 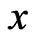 and the following inequality:
and the following inequality:
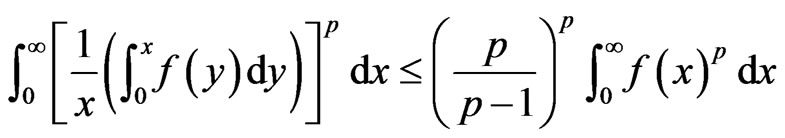 (1)
(1)
holds, where 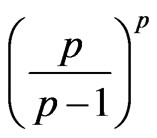 is the best possible constant (see [1]).
is the best possible constant (see [1]).
This inequality can be found in many standard books (see [2-7]). Inequality (1) has found much interest from a number of researchers and there are numerous new proofs, as well as, extensions, refinements and variants which is refer to as Hardy type inequalities.
In the recent paper [8], the author proved the following generalization which is an extension of [9].
Theorem 2 Let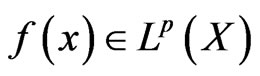 ,
, 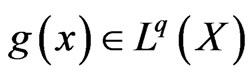 and
and 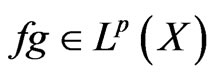 be finite, non-negative measurable functions on
be finite, non-negative measurable functions on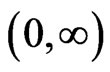 ,
, 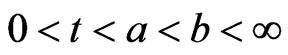 and
and 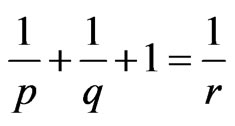
with 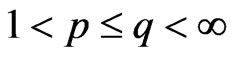 such that
such that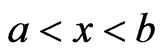 . Then, the following inequality holds:
. Then, the following inequality holds:
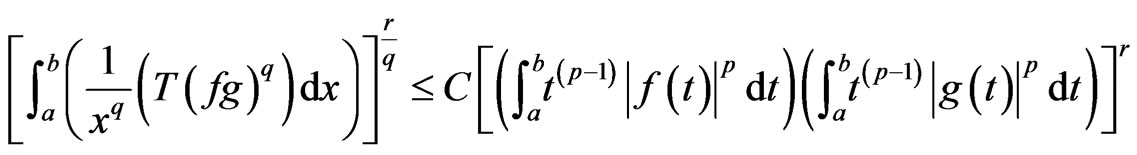 (2)
(2)
where,
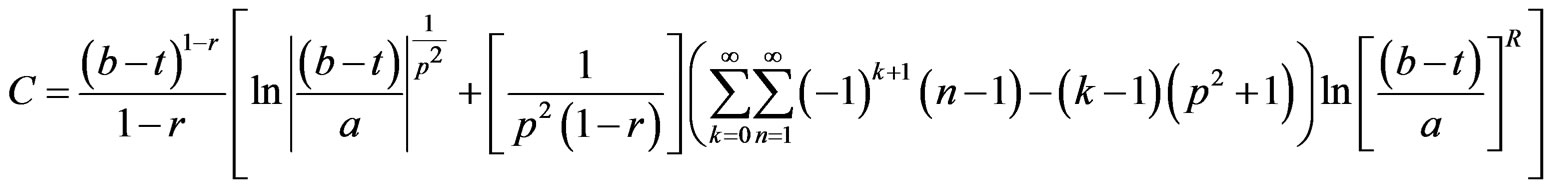
and
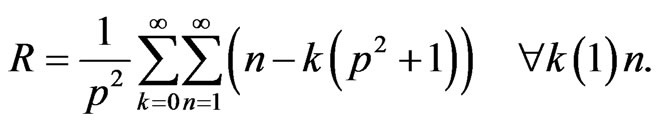
[10] also proved the following integral inequality of Hardy-type mainly by Jensen’s Inequality:
Theorem 3 Let 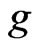 be continuous and nondecreasing on
be continuous and nondecreasing on 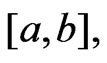
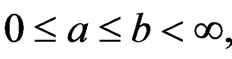 with
with 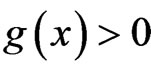 for
for 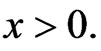 Let
Let 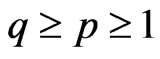 and
and  be nonnegative and LebesgueStieltjes integrable with respect to
be nonnegative and LebesgueStieltjes integrable with respect to 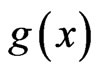 on
on 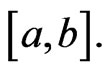
Suppose 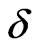 is a real number such that
is a real number such that 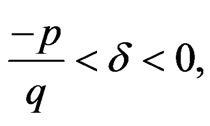 then
then
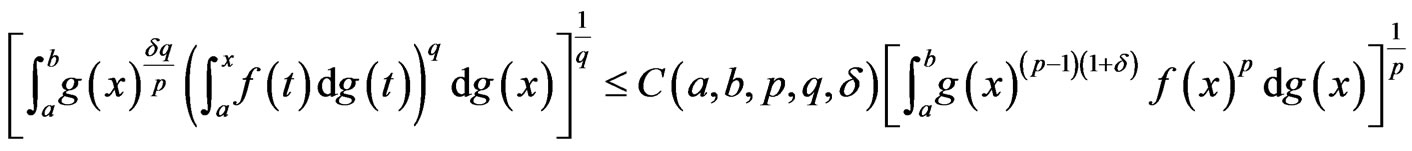 (3)
(3)
where,
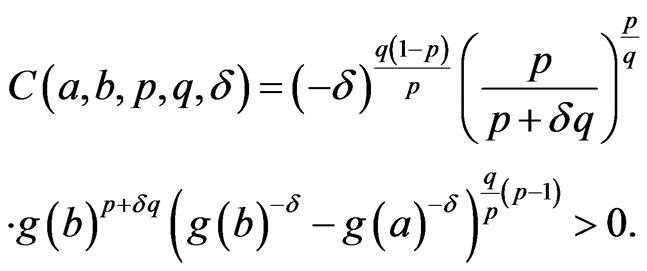
Other recent developments of the Hardy-type inequalities can be seen in the papers [11-16]. In this article, we point out some other Hardy-type inequalities which will complement the above results (2) and (3).
2. Main Results
The following lemma is of particular interest (see also [8]).
Lemma. Let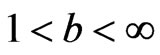 ,
, 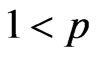 ,
,  , and let
, and let
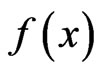 be a non-negative measurable function such that
be a non-negative measurable function such that
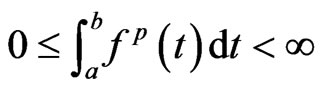 . Then the following inequality holds:
. Then the following inequality holds:
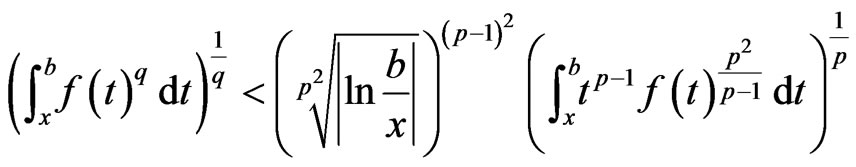 (4)
(4)
Proof
Let
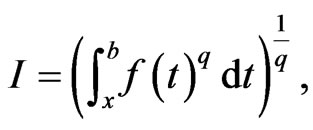
then,
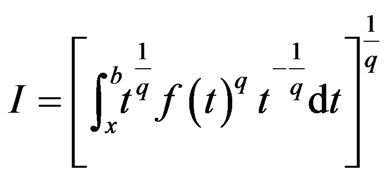
by Holder’s inequality, we have,
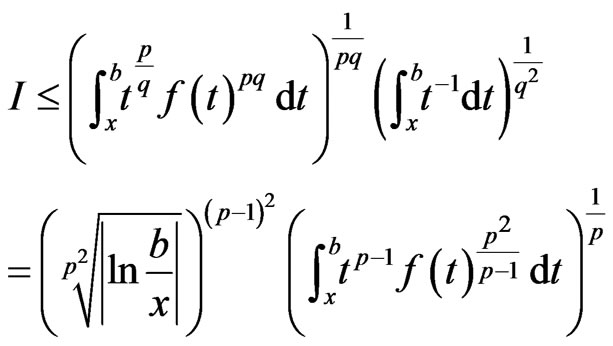
We need to show that there exists 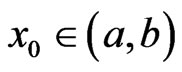 such that for any
such that for any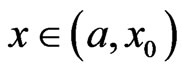 , equality in (4) does not hold. If otherwise, there exist a decreasing sequence
, equality in (4) does not hold. If otherwise, there exist a decreasing sequence 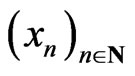 in
in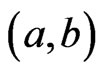 ,
, 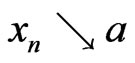 such that for
such that for 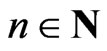 the inequality (4), written
the inequality (4), written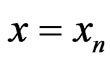 , becomes an equality. Then, to every
, becomes an equality. Then, to every 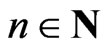 there correspond real constants
there correspond real constants 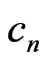 and
and 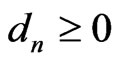
not both zero, such that 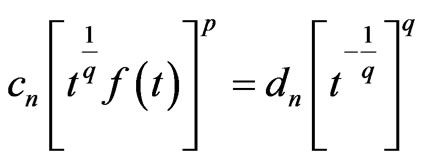 almost everywhere in
almost everywhere in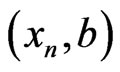 .
.
There exists positive integer N such that for 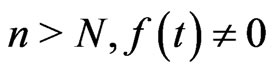 almost everywhere in (x,b). Hence,
almost everywhere in (x,b). Hence, 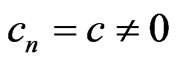 and
and 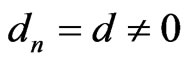 for
for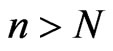 , and also
, and also
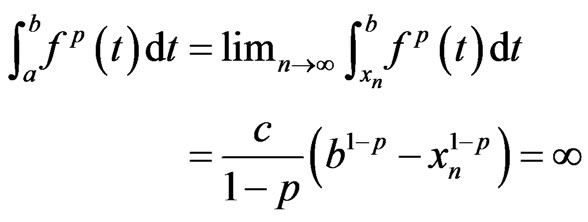
This contradicts the facts that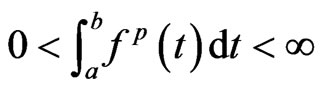 . The lemma is proved.
. The lemma is proved.
Theorem 4 Let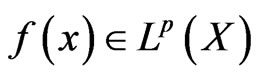 ,
, 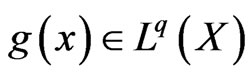 be finite non-negative measurable functions on
be finite non-negative measurable functions on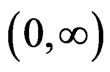 ,
,
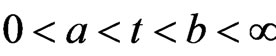 and
and  with
with 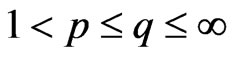
such that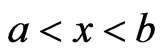 , then the following inequality holds:
, then the following inequality holds:
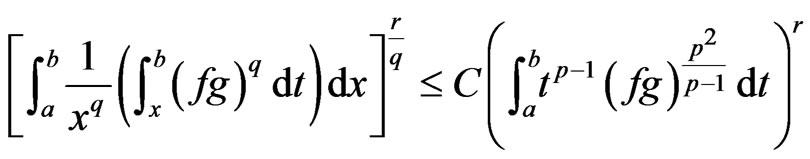 (5)
(5)
where
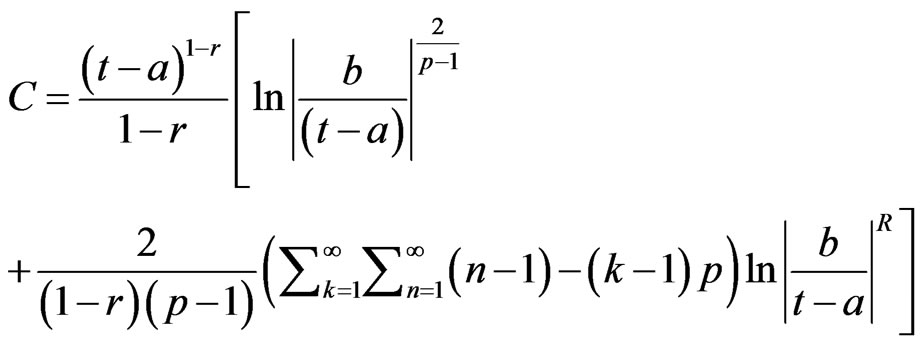
and
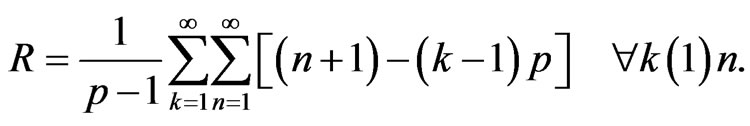
Proof
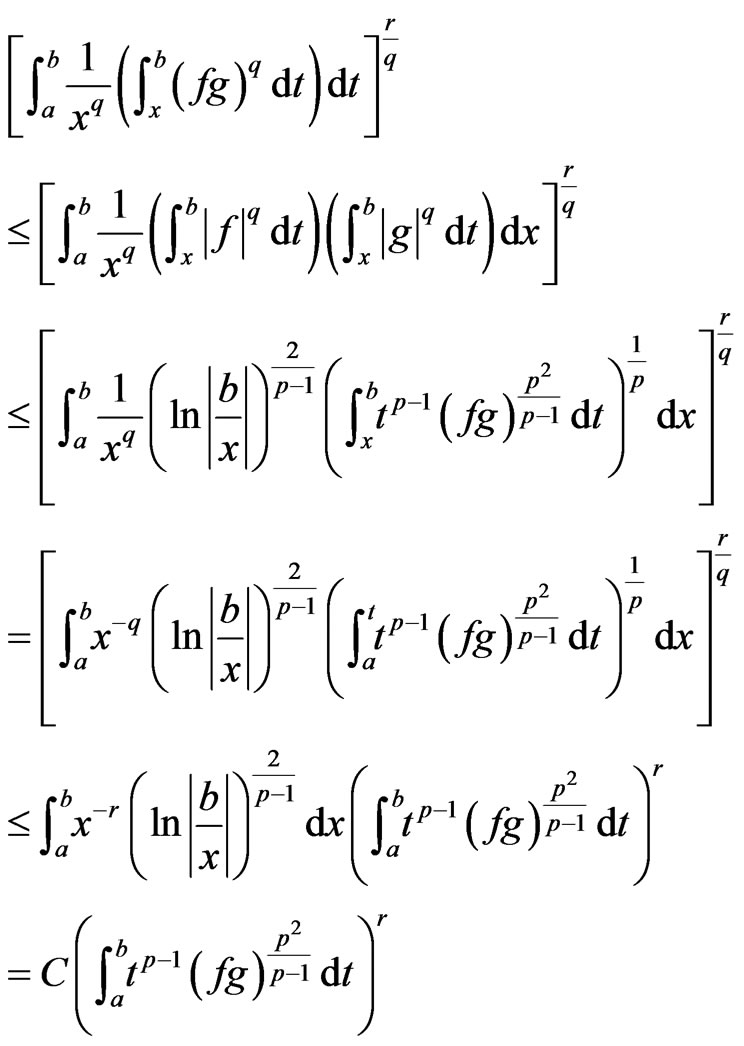
where C is as stated in the statement of the theorem and this proves the theorem.
The next results are on convex functions as it applies to Hardy-type inequalities.
Lemma. local minimum of a function f is a global minimum if and only if f is strictly convex.
Proof
The necessary part follows from the fact that if a point 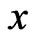 is a local optimum of a convex function
is a local optimum of a convex function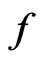 . Then
. Then 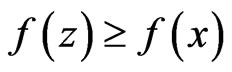 for any
for any 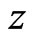 in some neighborhood
in some neighborhood 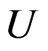 of
of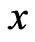 . For any
. For any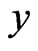 ,
, 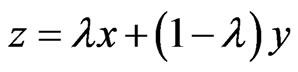 belongs to
belongs to 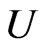 and
and 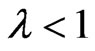 sufficiently close to
sufficiently close to 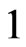 implies that
implies that 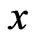 is a global optimum. For the sufficient part, we let
is a global optimum. For the sufficient part, we let 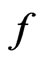 be a strictly convex function with convex domain. Suppose
be a strictly convex function with convex domain. Suppose 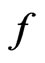 has a local minimum at
has a local minimum at 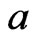 and
and 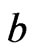 such that
such that 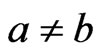 and assuming
and assuming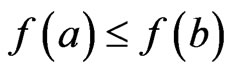 . By strict convexity and for any
. By strict convexity and for any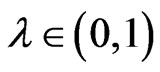 , we have,
, we have,
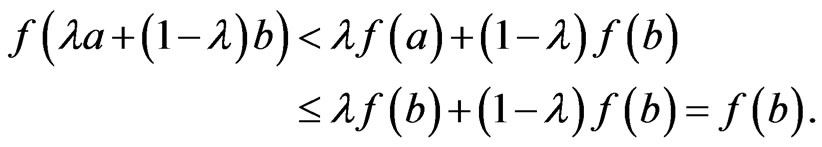
Since any neighborhood of 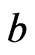 contains points of the form
contains points of the form 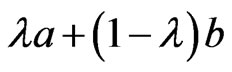 with
with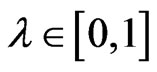 , thus the neighborhood of
, thus the neighborhood of 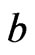 contains points
contains points 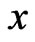 for which
for which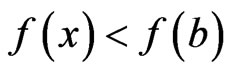 . Hence,
. Hence,  does not have a local minimum at
does not have a local minimum at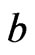 , a contradiction. It must be that
, a contradiction. It must be that , this shows that
, this shows that 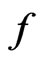 has at most one local minimum.
has at most one local minimum.
Lemma. Let 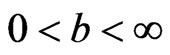 and
and . If
. If 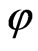 is a positive convex function on (a,c), then
is a positive convex function on (a,c), then
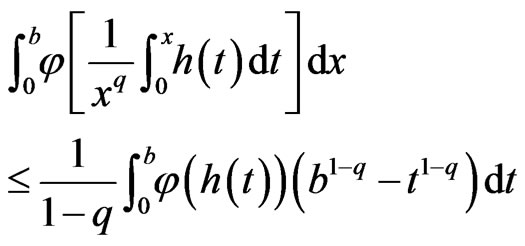 (6)
(6)
Proof
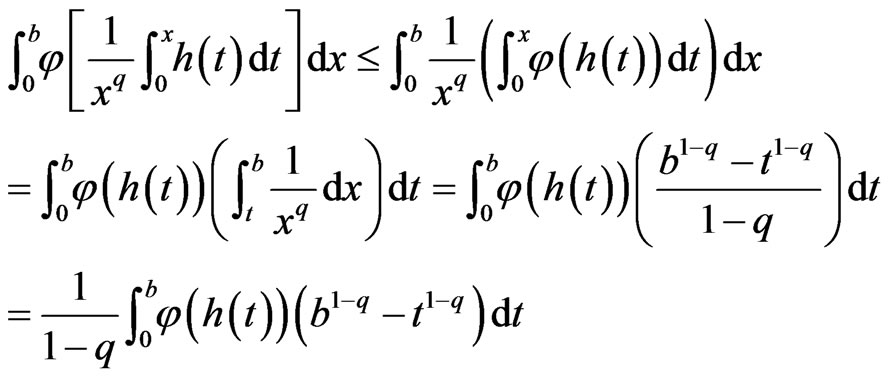
Hence the proof.
Lemma. Let 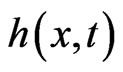 be non-negative for
be non-negative for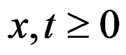 ,
, 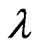 non decreasing and
non decreasing and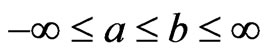 . then
. then
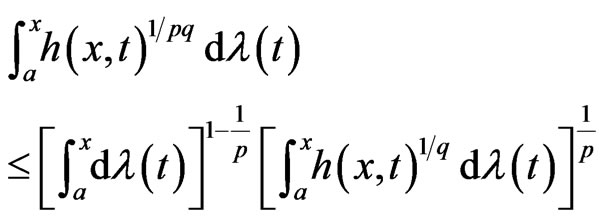 (7)
(7)
Proof
Let 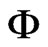 be continuous and convex, If
be continuous and convex, If  has a continuous inverse which is neccessarily concave, then by Jensen’s inequality we have
has a continuous inverse which is neccessarily concave, then by Jensen’s inequality we have
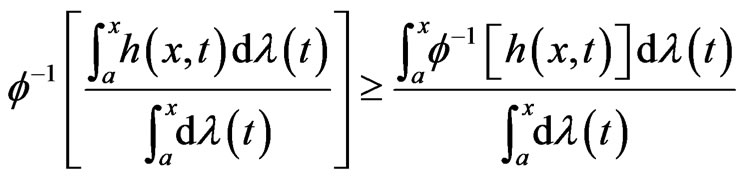
Taking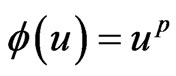 ,
, 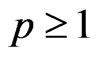 , we obtain
, we obtain
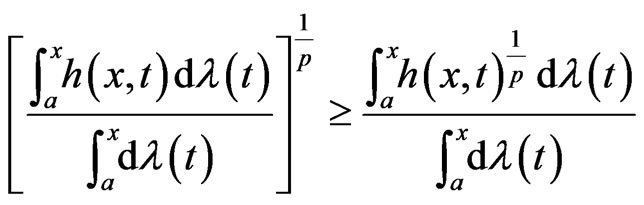
for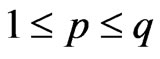 , we have
, we have
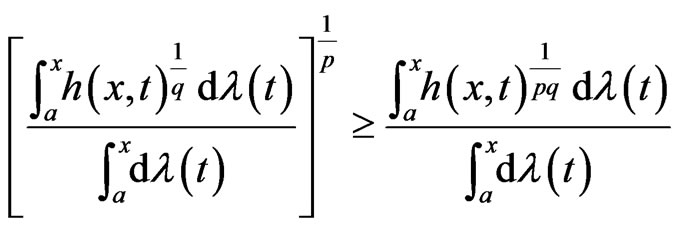
which we write as
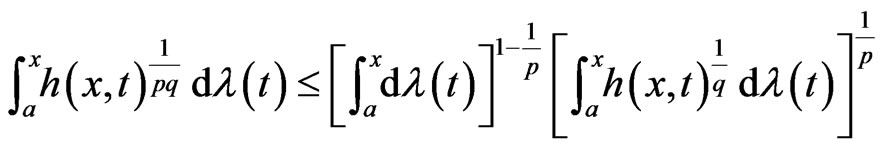
This complete the proof.
Theorem 5 If 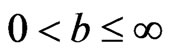 and
and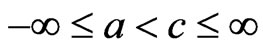 , let f, g be defined on (0,b) such that
, let f, g be defined on (0,b) such that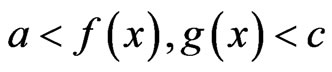 , then
, then
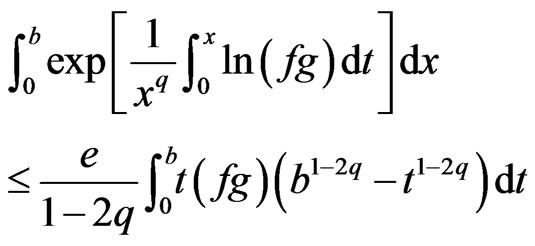 (8)
(8)
Proof

Since 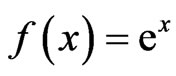 is a convex function, applying Jensen’s inequality to the above gives
is a convex function, applying Jensen’s inequality to the above gives
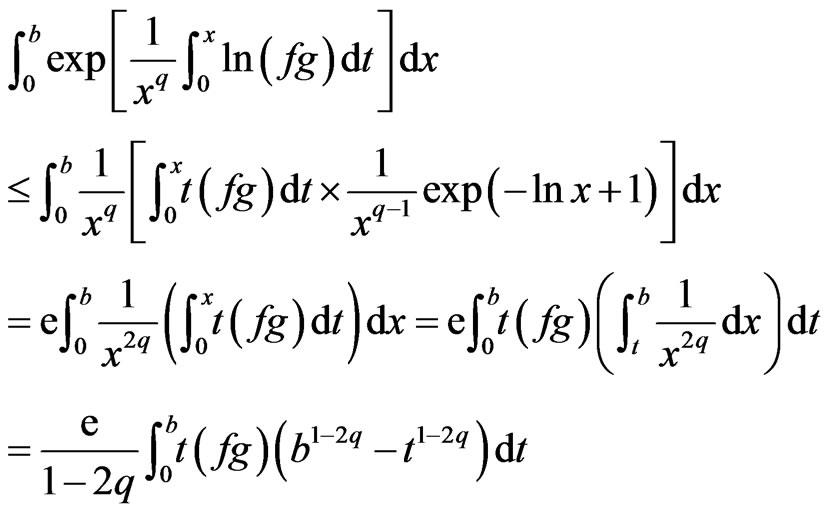
The result follows.
Theorem 6 Let g be a continuous and nondecreasing on ,
,  , with
, with 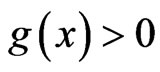 for
for 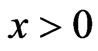 and
and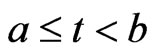 . Let
. Let 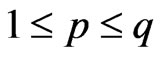 and
and 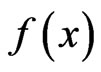 be nonnegative and Lebesgue-Stieltjes integrable with respect to
be nonnegative and Lebesgue-Stieltjes integrable with respect to 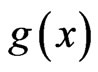 on
on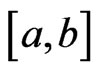 . Suppose r is a real number such that
. Suppose r is a real number such that 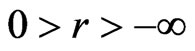 then,
then,
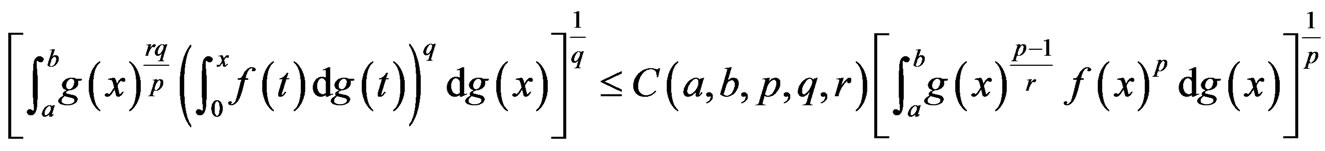 (9)
(9)
where
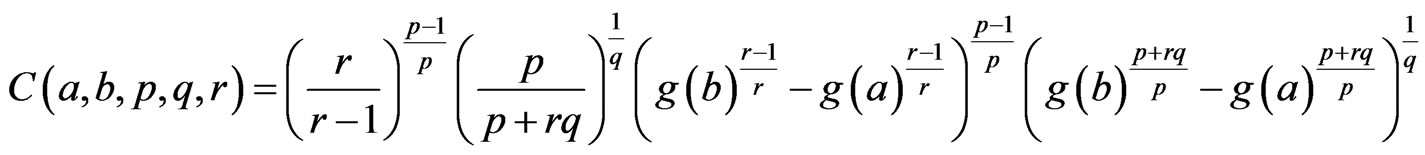
Proof
In the inequality (2.5), we let
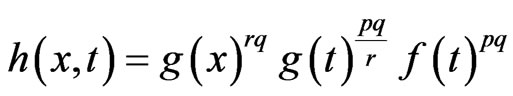
and
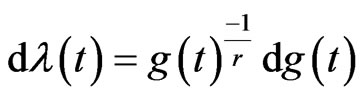
Then, the left hand side of (2.5) becomes
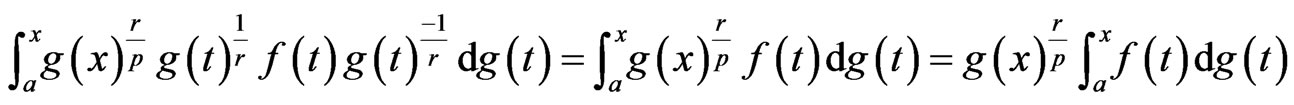
and the right hand side reduces to
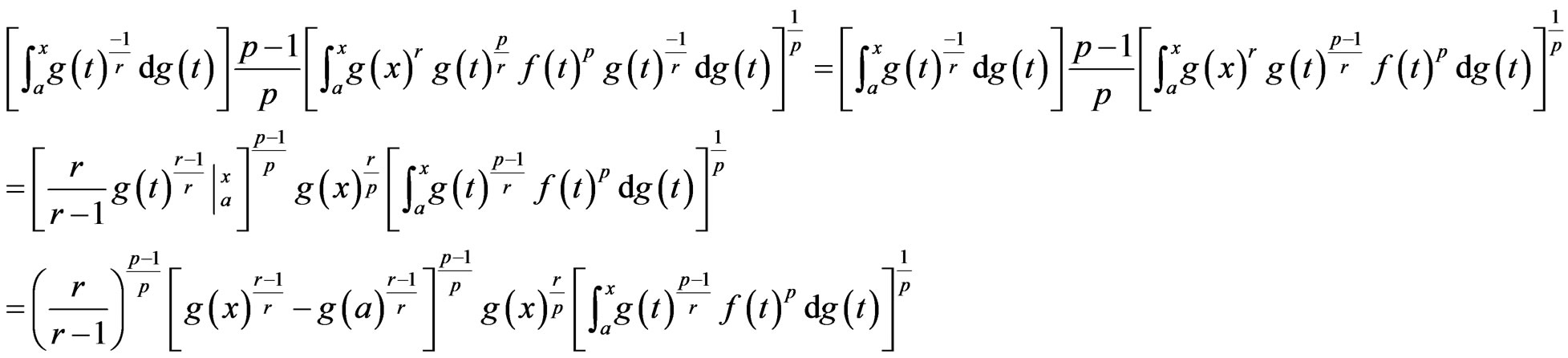
Hence, inequality (2.5) becomes
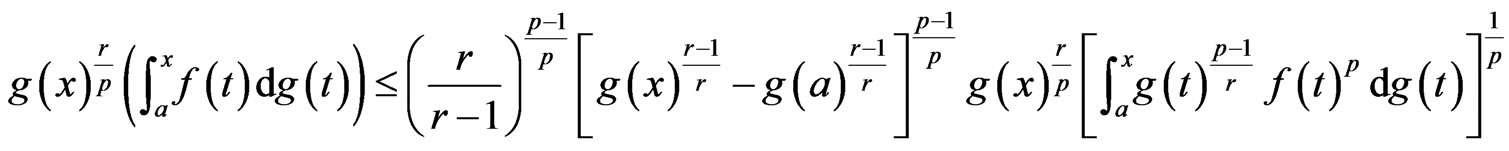
for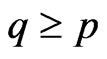 , we have
, we have
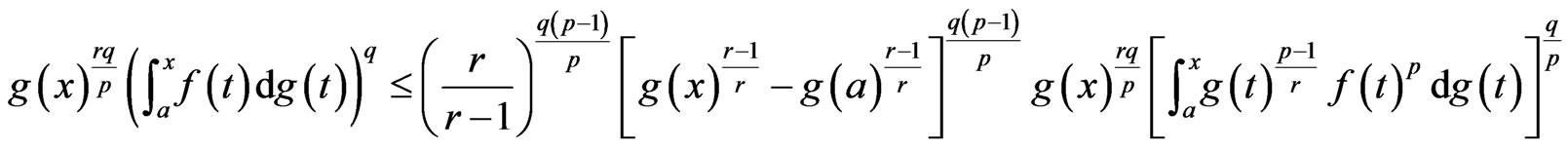
Integrating both sides with respect to 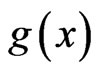 and then raising both sides to power
and then raising both sides to power  yields
yields
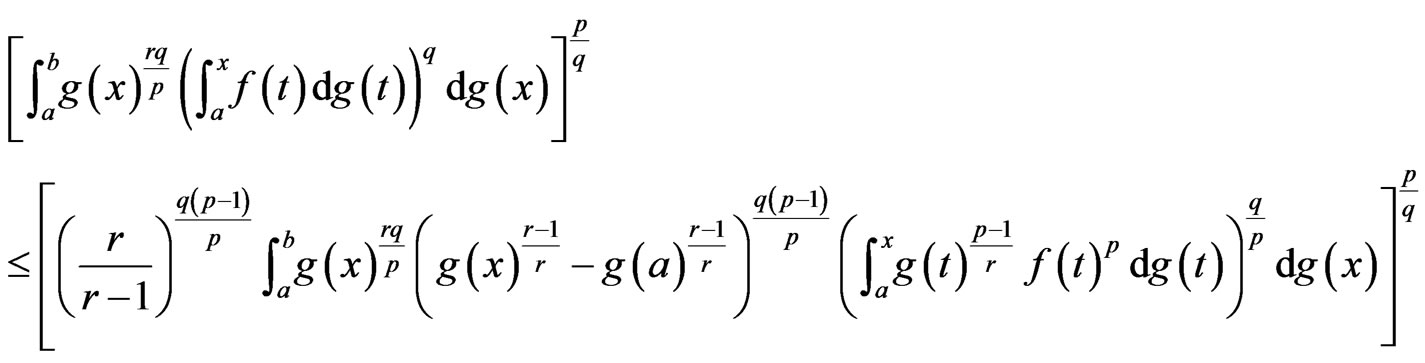
Applying Minkowski integral inequality to the right hand side implies
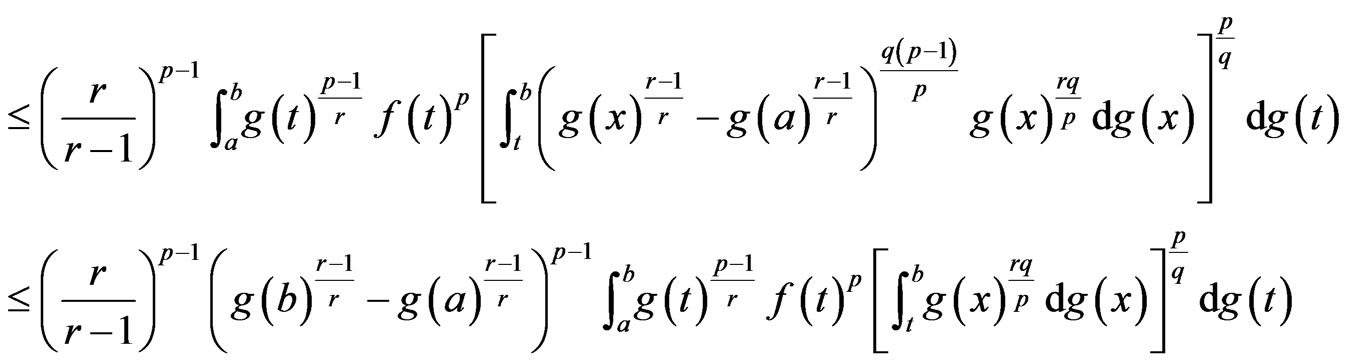
Since 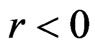
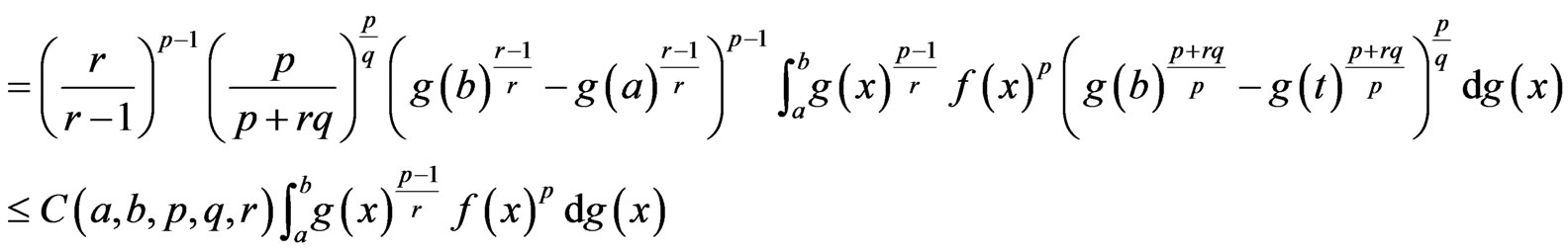
Hence, we have
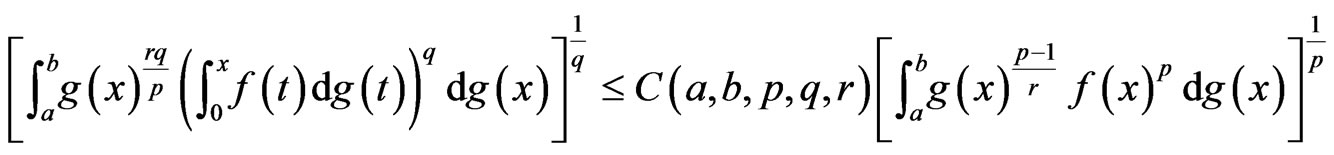
Which complete the proof of the Theorem.
3. Conclusion
This work obtained considerable improvement on AdeagboSheikh and Imoru results and applications for measurable and convex functions are also given.
REFERENCES
- G. H. Hardy, “Notes on a Theorem of HILBERT,” Mathematische Zeltschrift, Vol. 6, 1920, pp. 314-317.
- R. A. Adams, “Sobolev Spaces,” Academic Press, New York-London, 1975.
- G. H. Hardy, J. E. Littlewood and G. Polya, “Inequalities,” Cambridge University Press, Cambridge, 1952, MR0046395(13:727e), Reprinted 1991.
- A. Kufner and L.-E. Persson, “Weighted Inequalities of Hardy Type,” The American Mathematical Monthly, World Scientific, New Jersey, London, Singapore, Hong Kong, 2003. http://dx.doi.org/10.1142/5129
- A. Kufner, L. Maligranda and L.-E. Persson, “The Hardy Inequality—About Its History and Some Related Results,” Vydavatelsky Servis Publishing House, Pilsen, 2007.
- C. P. Niculescu and L.-E. Persson, “Convex Functions and Their Applications. A Contemporary Approach,” Springer, Berlin, Heidelberg, New York, Hong Kong, London, Milan, Paris, Tokyo, 2005.
- B. Opic and A. Kufner, “Hardy Type Inequalities,” Longman, Harlow, 1990.
- K. Rauf, J. O. Omolehin and J. A. Gbadeyan, “On Some Refinement of Results on Hardy’s Integral Inequality,” International Journal of Scientific Computing, Vol. 1, No. 1, 2007, pp. 15-20.
- Y. Bicheng, Z. Zhuohua and L. Debnath, “Note on New Generalizations of Hardy’s Integral Inequality,” Journal of Mathematical Analysis and Applications, Vol. 217, No. 1, 1998, pp. 321-327. http://dx.doi.org/10.1006/jmaa.1998.5758
- A. G. Adeagbo-Sheikh and C. O. Imoru, “An Integral Inequality of the Hardy’s Type,” Kragujevac Journal of Mathematics, Vol. 29, 2006, pp. 57-61.
- S. S. Dragomir and N. M. Ionescu, “Some Converse of Jensen’s Inequality and Applications,” Revue d'Analyse Numérique et de Théorie de l’Approximation, Vol. 23, No. 1, 1994, pp. 71-78.
- C. O. Imoru and A. G. Adeagbo-Sheikh, “On Some Weighted Mixed Norm Hardy-Type Integral Inequalities,” Journal of Inequalities in Pure and Applied Mathamatics, Vol. 8, No. 4, 2007, pp. 1-12.
- S. Kaijser, L. Nikolova, L.-E. Persson and A. Wedestig, “Hardy-Type Inequalities via Convexity,” Mathematical Inequalities & Applications, Vol. 8, No. 3, 2005, pp. 403- 417.
- K. Rauf and J. O. Omolehin, “Some Notes on an Integral Inequality Related to G.H. Hardy’s Integral Inequality,” Punjab University Journal of Mathematics, Vol. 38, 2006, pp. 9-13.
- M. Z. Sarkaya and H. Yildirim, “Some Hardy Type Integral Inequalities,” Journal of Inequalities in Pure and Applied Mathematics, Vol. 7, No. 5, 2006, pp. 1-5.
- L. Zhongxue, G. Mingzhe and L. Debnath, “On New Generalizations of the Hilbert Integral Inequality,” Journal of Mathematical Analysis and Applications, Vol. 326, No. 2, 2007, pp. 1452-1457. http://dx.doi.org/10.1016/j.jmaa.2006.03.039

