ABSTRACT

The role of nonlinearities in the dynamics of the non-equilibrium systems is considered. Various types of nonlinearities for dynamical systems with holonomic and nonholonomic constraints are studied. Features of the nonlinearity responsible for the evolution of the systems to the equilibrium are considered. The interrelation of the nonlinearities with the concepts of symmetry breaking is analyzed. Mathematical justification of the irreversibility of the dynamics of systems is offered. Peculiarities of nonlinear nonequilibrium systems connected with hierarchical structure of natural objects are studied.

Keywords:

Nonlinear, Nonequilibrium Dissipative Classical Mechanics, Holonomicity

1. Introduction

Natural systems in generally are open and nonequilibrium. Evolutionary pro- cesses of emergence and development of new structures are inherent to them. These processes are nonlinear because they are associated with increasing of the entropy but the increment of the entropy is determined by the infinitesimal quadratic nonlinear terms [1] . Therefore, the study of the natural evolutionary phenomena is impossible without the development of the mathematical apparatus for solving systems of nonlinear differential equations. Despite the considerable efforts to develop methods for solving nonlinear equations [2] [3] [4] [5] , there are no methods to solve them today. There are only a limited number of such equations, for which it is possible to obtain an analytical solution [5] [6] .

As a rule, for solving systems of nonlinear differential equations, they reduced to integrable equations by replacing the variables. The choice of the independent variables is determined by the nature of the symmetry of equations. Most of the nonlinear equations are simplified by the linearization. Sometimes the simplifications of the models of the systems under study, or hypothesis for simplification of the systems of equations are used. As a rule, with such simplifications, the nonlinear effects that determine the evolution of the system are lost. For example, the use of the hypothesis about holonomicity constraints in the construction of the canonical formalisms for a system of material points (MP) has led to the exclusion of nonlinear terms, responsible for dissipative processes [7] . As a result, the description of the irreversible evolution of open nonequilibrium systems within the formalism of classical mechanics became impossible [7] [8] .

The development of computer technology helps to solve nonlinear equations using numerical methods. However, numerical methods are convenient for pra- ctical applications or checking theoretical conclusions but they almost did not disclose the physical nature of the process.

The difficulty of the analytical solutions of nonlinear equations led to the development of qualitative methods of analysis. They, in particular, used to identify the statistical regularities of systems dynamics for the study of their phase portraits. These methods are effective in the study of dynamical chaos. They are also widely used for bifurcation analysis, for studying the characteristics of the nonlinear equations and for seeking of new nonlinear effects [3] [9] [10] .

The presence of the universal laws of evolution of systems, regardless of whe- ther these are objects of the universe, or it is the atomic system [11] , indicates on the universality of non-linear processes. This means the possibility the existence of universal methods for solving nonlinear equations. To find these techniques, the classification of different types of nonlinearities in line with the nature of the physical process can be useful. Such a classification is useful also for studying the nonlinear processes of evolution of systems in nature, for the development of physical theories of the foundations of evolutionary processes in open nonequilibrium systems [12] . The classification of the nonlinearities and corresponding processes can help to simplify the corresponding equations, not excluding the possibility of studying the effects associated with the evolution and to develop analytical and numerical methods for solving nonlinear equations, basing on the knowledge of the nature of the processes.

The classification of the different types of the nonlinearity is possible to realize by starting from the analysis of the physical nature of the corresponding nonlinearities. The most natural criterion for separating the different types of nonlinearities, inherent for the dynamical systems of classical mechanics, is divide these systems in connection with holonomic and nonholonomic constraints. Accordingly, the first type of the nonlinearities consists from those nonlinearities, that inherent for the conservative Hamiltonian systems with the holonomic constraints. The second type of non-linearity consists of nonlinearities, which determines the dynamics of non-Hamiltonian systems with nonholonomic constraints. This type of non-linearity belongs to the dissipative systems [1] [8] .

The main purpose of the work is to analyze the class of the nonlinearities, responsible for the irreversible dynamical systems of the classical mechanics. For this purpose, we determine the nature of the class nonlinearities which response for irreversibility. The connection between the nonlinearities and irreversibility of the systems dynamic will be analyzed also. The characteristics of these nonlinearities for nonequilibrium systems (NS), taking into account their hierarchical structure, will be studied.

2. Nonlinearities for Hamiltonian and Non-Hamiltonian Systems

The possibility of integrating the dynamics equations of the classical mechanics is determined by the properties of the system itself and by the nature of the restriction that are imposed on the system. The restrictions are divided on the holonomic and nonholonomic.

Holonomic constraints are such restrictions, which can be expressed through the full differential of the spatial variables. For systems with holonomic constraints, the task is reduced to the solution of independent equations for the generalized independent variables. Hypothesis about holonomicity constraints is used for obtain the Lagrange and Hamilton canonical equations [13] .

For Hamiltonian systems, the energy of each element is invariant. The nonlinearities, existing in Hamiltonian systems, causes fragmentation of scale that characterizes the dynamics of each individual element [12] [14] . An example of Hamiltonian systems is a system of non-interacting of oscillators. Therefore, the canonical formalisms of classical mechanics do not apply for the study of nonlinear processes responsible for the evolution, because evolution is possible for the interaction elements. Interactions of components lead to the dissipation and the presence of attractors, which is a characteristic feature of evolution. Thus, the hypothesis of holonomic constraints leads to the fact that canonical Lagrange and Hamilton equations cannot be applied to analysis of the irreversible pro- cesses [14] [15] [16] [17] .

Non-holonomic constraints cannot be expressed through the total differential of a function of space variables [13] [18] . Uncouple generalized variables for nonholonomic systems are impossible. Non-holonomic constraints mean presence a nonlinear transformation of energy between elements of the system. The total energy of the system elements, rather than energy of a single element, is an invariant of the system, i.e. the dynamic of the non-holonomic system, unlike holonomic, can only be nonlinear, because they are characteristic of the energy exchange between the system components or between interacting systems. These processes of the systems interaction are determined only by the nonlinear terms.

Thus, the nonlinearities responsible for the evolution of the NS to the equilibrium or for the interaction systems are inherent only for the systems with non- holonomic constraints. Since these nonlinearities responsible for the evolution of the system, we will call them “evolutionary nonlinearities”.

3. The Dynamic of the MP Systems and Non-Linearity

We will construct this work based on the mechanics of structured particles (SP), where SP is equilibrium system from a great enough number of the potentially interaction MP [14] [15] [16] . The essence of the mechanics of SP is that the base elements of the bodies for the motion equations are SP, unlike classical me- chanics where elements of bodies are MP. This mechanics allows studying the nonlinear dissipative processes, which inherent to the NS, basing on the laws of classical mechanics [14] [15] [19] .

The generality of the analysis of dynamics of systems of nonlinear equations of classical mechanics is that any non-equilibrium systems in the local thermodynamics equilibrium approach with sufficient accuracy can be represented by a set of interacting SP [1] [20] .

The motion of MP system is determined by the influence of two independent types of internal and external of forces. The internal forces are determined by the interaction of MP. The sum of these forces is equal to zero. External forces determine the motion of the system in space. The external forces may be different for different MP due to the inhomogeneity of the external field. In this case, the external forces will change the internal energy of the system. The internal motions of the MP in the system relative to the CM, do not contribute into the motion of the system in space.

Since the internal energy and the motion energy are independent, the energy of the system should be presented as the sum of the energy of motion of the system and of the internal energy. We can do this presentation of the energy with the help of independents macro- and micro-variables. The energy of the system that provided in these variables has the form [14] [15] :

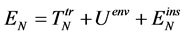(1)

where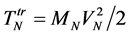,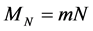; 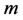is a mass of MP (let’s assume m = 1); is a number of MPs into SP; 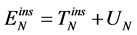is internal energy;

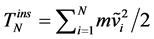is a kinetic component of the internal energy;

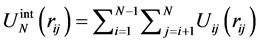is MPs interaction energy; 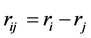is a distance between 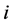-th and 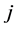-th MP; 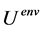is the potential energy of the external field, which depends on the micro- and macro-variables in general. By differentiating Equation (1) with respect to time and performing some conversion, we obtain [14] [15] :

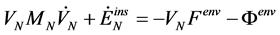(2)

where 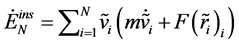is a change of the internal energy; 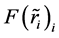is a force which acts on -th MP;, 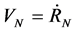are coordinates and velocities of the CM;, are coordinates and velocities of MPs;, are coordinate and velocity of -th MP relative to the CM;;; (Here we call as a force the gradient of the potential energy. Therefore, these forces are negative in relation forces which determined from forces potential function [18] ).

Let’s assume that, then, where is a scale of non-homogeneity of the external field. As we can see, is expanded on a small parameter. By retaining the terms of the zero and first order, we obtain

. Since

and, the following expression for Equation (2) takes place [15] :

(3)

We see that the second term on the right hand side of Equation (5) depends on the micro- and macro-variables. It is different from zero only when the existence of a gradient of external forces. It is because a change of internal energy of the bodies is possible only due to the difference of the external forces acting on the different elements of the system. It is not just a bilinear but bisymmetrical as it depends on the variables of two different groups of symmetry. The motion equation for the system can be obtained from Equation (2) [15] :

(4)

where is a coefficient which determines the change of the internal energy.

The first term in the right hand side of Equation (4) is a potential force, which applied to the CM of the system. The second term is determine the change of the SP’s internal energy and depends on both micro- and macro-variables. This nonlinear term is appeared due to taking into account of the internal energy of the system.

Equation (4) generalizes equation Aristotle and Newton. As Aristotle equation says that the speed of a body is proportional to the force. According to Equation (4) is true when the frictional force becomes equal to the driving force.

Newton’s equation states that the acceleration is proportional to force. This case is realized when external forces are uniform, or when the internal forces are large, so that the system can be considered a solid.

Let us compare the mechanics of SP [14] with classical mechanics of MP. For MP, the work of external forces goes only on its acceleration. However, for the system MP the work of external forces goes both on its acceleration and on the change of the internal energy. Therefore, the motion energy each MP, non-uni- quely determine the motion energy of SP because part of the energy of MP belong to the internal energy of SP. The sum of forces acting on MPs changes the motion energy of the system. But the internal energy is changes only in the case when we have difference of these forces for different MP. It is possible only in the non-homogeneous external field of forces and similar as excitation of the strings or oscillator [5] [7] . If the gradient of external forces is absent, Equation (6) is transformed into a reversible Newton equation. In an inhomogeneous field of force the motion equation is defines the transformation of the motion energy into the internal energy; i.e. the motion energy is not invariant. The invariant of the motion of the system is the total energy.

Nature of the “evolutionary nonlinearity” can be easily understood by the ex- ample of the oscillator in a non-uniform field of the force. To understand this nature the energy of oscillator should be expressed in terms of micro- and macro-variables as the sum of the motion energy and the internal energy. In the non-uniform external forces when the characteristics scales of irregularities of the forces are commensurate with the characteristics scale of oscillator, both types of energy are related. Depending on the initial phase, the oscillator is able to pass through the potential barrier, even when the energy of motion is less than the height of the barrier. This transition is carried out due to transformation of the internal energy into the motion energy [7] . Thus, these nonlinearities define the dissipation and symmetry violation of time [14] [21] .

We start from the condition that the symmetry breaking always connected with the violation of the invariance of the measure corresponding to this symmetry group. A measure of the translational symmetry in classical mechanics is the phase volume, or motion energy of the system. The violation of the invariance of the motion energy is a breaking of the time symmetry. In our case, a breaking of the time symmetry is due to transformation of the motion energy into internal energy. Such a transformation is determined by the second bilinear term of Equation (5), which is simultaneously dependent from the micro- and macro-variables.

4. Evolutionary Nonlinearity for Nonequilibrium Systems

Let us consider the dynamics of the nonequilibrium systems. In the approach of the local thermodynamic equilibrium, nonequilibrium system can be submitted as a set of the equilibrium subsystems SP, which in the relative motion to each other (Figure 1) [1] [20] . Then to describe the dynamic of nonequilibrium systems, we can use the motion equations for SP Equation (6). For nonequilibrium systems, the work of the external forces will go on the motion and on the change of the internal energy. The energy of nonequilibrium systems is equal to the sum of the SP energy. The energy of SP consists from the SP motion energy in the external field of force, from the motion energy of SP in the field of force of another SP, and from the internal energy.

Let us consider nonequilibrium system consists from MP. All MP redistributes between K SP. i.e. p = 1, 2, 3 … K, where p is a number of SP. Each p-SP is consists from L_p number of MP, i.e. l = 1, 2, 3 … L_p; is a coordinates of CM for nonequilibrium system;; R_p is coordinates of CM for p-SP relative to the CM of nonequilibrium system; is a coordinates of l-MP relative CM of p-SP; is a coordinate of CM of nonequilibrium system. The velocity of -МP is equal to where is a velocity of CM for p-s SP relative to the CM of nonequilibrium system, is a velocity of -s MP relative to the CM of p-s SP. In these variables, the energy of nonequilibrium system can be written as:

(5)

Here is a mass of p-SP; is a potential energy of p-SP, which determined by interaction all its MP; is a distance between and MP; is energy of potential interaction of and SP. The indexes and belong to MP from different SP,.

The first term in Equation (5) is motion energy of nonequilibrium system. The second term is a sum of internal kinetic energy of SP. The third term defines of the kinetic component of the internal energy of each MP. The fourth term is the sum of the internal potential energy of all SP. It is determined by summing the indices corresponding for SP. The fifth term is the potential energy of interaction of SP. The term is a sum of the potential energies of all SP in the field of external forces, is a potential energy p-SP in the field of external forces.

As in the case of SP, the motion equation of the nonequilibrium system can be obtained from the energy Equation (5) which represented by the hierarchy of the micro- and macro-variables. The internal energy of the nonequilibrium system is divided into the sum of the SP motion energies and their internal energy. This means that the energy of the external field go on the change the motion energy of nonequilibrium system, on the change of the energy of SP relative motion and on the change of the internal energy of SP. The last two types of energy is the internal energy of the nonequilibrium system, i.e. in the nonequilibrium system, in contrast to the SP, there is an additional hierarchical level. It leads to a hierarchy of energy and entropy of the nonequilibrium system.

The phase space of nonequilibrium system is determined by coordinates and velocity of CM for SP. It was called S-space [14] . The dimension of S-space is 6K −1. For SP, in addition to changing of the velocity of the CM, the internal energy also changes. The micro- and macro-variables are independent. The compression determined by the extended Liouville equation for the SP [19] . Only when the internal energy of the SP is not changed, the S-space coincides with the usual phase space. Therefore, the one point of the S-space corresponds to different values of internal energy of the SP. This ambiguity is possible to eliminate if to the S-space add by the space of the micro variables, determining motion of all MP relative of CM for SP.

5. The Nature of the Irreversibility of Nonequilibrium Systems

The physical nature of the irreversibility of SP dynamics in an inhomogeneous field of external forces was enough to set out in detail in [14] [22] . Here, based on evolutionary nonlinearity, consider the nature of the irreversibility of the NS.

According to the statistical physics, the closed NS tend to equilibrium, which corresponds to zero relative velocities of all SP. That is, the kinetic energy of the relative motions of the SP, 0 when [1] . This is proved by the variation of the entropy of the NS under the condition its maximum value in the equilibrium state, i.e. in the statistical physics, the proof of the equilibration of the NS is constructed using the condition that the equilibrium corresponds to the maximum entropy and the state with the maximum entropy corresponds to a state in which the system is the maximum time. At the same time, under the laws of mechanics, the equilibration of the NS explains by the fact that when the SP in an inhomogeneous field of force its internal energy can increase due to the non-linear transformation of the motion energy into internal energy [14] .

Now let us show how the equilibration of the system follows from the evolutionary nonlinearity. For this purpose we consider the motion SP in an inhomogeneous field of forces. According to Equations (3) and (4) the motion energy of the SP can be converted into the internal energy. Suppose that the value of this transformation is equal to. The value is determined by bilinear terms of the expansion of the field of external forces, which depend on micro- and macro-variablesles. So it has the second order of smallness. It can be written as, where, is a small parameter, for example, the ratio of the characteristic scale of the SP to the characteristic scale of inhomogeneity of the external field of forces. We emphasize that this conclusion corresponds to the change in entropy of the system, which has a second order of smallness [1] [20] .

If the field of external forces is small, the equilibrium violation for SP can be ignored. This means that the energy of its motion is irreversible converted into the internal energy. But with sufficient quantities of forces and their gradients, equilibrium of the SP can be broken. In this case, it can represent as a set of equilibrium subsystems having nonzero relative velocity. Then the increase in the internal energy of the system is the sum of the increments of energy relative motion of equilibrium subsystems and their internal energies. We write it like this: where is the increment of energy relative motions of equilibrium subsystems, and is increment of internal energy of equilibrium subsystems. Consequently, the inequality: < have a place.

Only the energy of the relative motions of equilibrium subsystems can go back into the energy of motion of the full system because the internal energy of the equilibrium system cannot be going into the motion energy of this system due to momentum conservation. Let the return energy is equal to. The value is also determined by a nonlinear function of the micro- and macro-variables that characterize the motion of the whole system and equilibrium subsystems consequently. Here are the micro variables determining the motion equilibrium subsystems with respect of CM system, and macro-variables determine the motion of the CM of SP. Since forward and reverse energy flows are determined by bilinear terms, then also will be determined by the terms not less than quadratic power terms. But is a term of at least second order of smallness. Therefore, is not lower than fourth order. Hence we have. Consequently, for sufficiently large systems the inequality << will take place. This leads to equilibration, and hence to an increase in entropy of SP in the non-homogeneous field of the external forces.

Let us explain why the increase of the internal energy becomes irreversible only for the big enough systems.

According to the law of statistical physics, the fluctuations in the value of the energy are proportional to the, where -is a number MP in a system [1] . This means that fluctuations and will be determined by the value. The inequality > holds only on average. For sufficiently small, the fluctuating value of the reverse flow of energy relative movements SP into the energy of motion, at some point of the phase space may be greater than the value of the fluctuating motion the flow of energy into internal energy (where the sign, , used to indicate the fluctuations of the corresponding quantities). That is, for sufficiently small, in some cases there may be inequality, despite the fact that in average the value of in two orders of magnitude higher than. However, with increasing number of particles in the system, the fluctuations are reduced and the inequality < not violated. But according to the numerical calculations D-entropy, this conclusion is also following from motion equations for SP Equations (3) and (4) [14] [22] . Thus, the tendency of the system to an equilibrium state corresponding to the maximum probability arises from the laws of mechanics!

It is necessary to emphasize that the only condition that was used for proving of violations of equality forward and reverse energy flow in a sufficiently large system, moving in a non-uniform force field, was the condition of inability to transform the internal energy of an equilibrium system in its kinetic energy. It is equivalently to the statement of inability transformation of the thermal energy into the body’s energy of motion due to law of momentum conservation. This provided us an opportunity to introduce the concept of entropy in classical mechanics. Let us briefly explain how this was done.

The entropy in classical mechanics was called as D-entropy. D-entropy is defined as the ratio of the increment of internal energy of the system at the expense of the energy of motion to the value of the internal energy. Expression of D-entropy has the form [17] :

(6)

is internal energy of p-SP; is external MP for p-SP which interaction with the -th MP from p-SP; -is a force changing the velocity of -th MP relative of CM p-SP. This force acted from the -МP another SP; is a velocity -th МP relative CM of SP.

The amount of D-entropy is determined by summing over the part of the work of external forces that is goes to the change internal energy of the NS. D- entropy is a deterministic because its follows from the motion equations of the system.

Determination of D-entropy is acceptable for small systems. However, for them the D-entropy, in contrast from the entropy of Clausius, may be both positive and negative. The oscillator is example of small systems. The energy of the relative motion of the elements of oscillator, which is the internal energy of the oscillator, in a non-uniform field of force can goes into its motion energy [7] . For systems from a sufficiently large number of MP, D-entropy up to a numerical factor is equal to the entropy of Clausius and can be expressed in terms of temperature and function of heat.

D-entropy can be used to determine the limits of applicability of the thermodynamic description of the system, the limits of applicability of the laws of statistical probability. This is confirmed by the numerical calculations of the change of the internal energy of the system depending from the number of MP when the system is moving in the inhomogeneous field of external forces.

6. Hierarchical Structure of Matter

The possibility of transformation of the motion energy of the NS into the internal energy depends on the characteristic scale of the inhomogeneity of the external field of forces and the characteristic scales of the NS (Figure 1).

Let the scale of the NS is. If then internal energy of the NS does not change and all the work of the field of external forces goes on motion of the NS.

When, where is a characterized scale of SP (Figure 1), the internal energy of the NS system is increased by increasing the energy of the relative motion of the SP. In this case, the external field of force does not change the internal energy of the SP.

If the external field of force changes not only the energy of the relative motion of SP, but also change the internal energy of the SP.

It is follows from the mechanics of the SP that according to the laws of classical mechanics, the matter is infinitely divisible [14] . The infinite divisibility of matter follows from the impossibility of formation of an attractor for systems from elements that no have a structure [23] . The idea of the infinite divisibility subsequently expressed also in the work, which substantiates the existence of the mass for photon [23] . The infinite divisibility means that MP should be regarded as a system consisting from elements that also have a structure, and so to the infinity. That is, the bodies represent the infinite hierarchy of embedded systems with the hierarchy of the characteristic scales, which is a numbers of the hierarchical levels that tends to infinity. The degree of hierarchy corresponds to the degree of non-linearity. Each hierarchical level, as a rule, corresponds to other forces. For example, the hierarchy molecules, atoms, the nucleus are determined by respective molecular, atomic, nuclear forces. For the hierarchy of forces with increasing scale the forces reduced. Matter is stable due to the large difference of forces on each hierarchical level. This difference is connected with evolutionary nonlinearities. The degree of hierarchy, “n”, which manifests itself in a concrete evolutionary process, is determined by the order of the expansion of the external forces. Than higher harmonics of the force expansion, the deeper on the hierarchical ladder is the change in internal energy of the system. In practice, the value “n” will be limited by the required accuracy for describe the dynamics system.

The nonlinear terms defining the process of transformation of the body’s motion energy into their internal energy are functions of the variables hierarchical levels. Therefore, D-entropy, and different types of energies are defined, in general, by the variables for the all hierarchical levels. The dynamics of the body is determined by the dualism of energy on any hierarchical level, because the work of external forces for any hierarchical element going both on its motion and on the change of the internal energy.

Evolution of the bodies is connected with the non-linear transformation of the flows of external energy into internal energy of its structural elements arranged in the hierarchy. Therefore, the description of the evolution is a self-consistent nonlinear dynamic task. That is, the field of forces created by the structure the nested hierarchical elements of the system, defines the structure of the system, as well as the structure of the system is determined by the hierarchy of the field of forces.

The conditions of stationary of the body structures, requires a balance of incoming and out-going energy flows at all hierarchical levels. These flows are hierarchically chain of non-linear transformations of the body’s motion energy. Therefore, for stationary the compensation of dissipative processes for the all hierarchical levels is necessary. It is only known the electromagnetic radiation for the body, which can to compensate the energy inflow into the bodies [20] .

A key role in the dynamics of systems plays symmetry. The nature of the transformation of energy at all hierarchical levels is determined by the external symmetries and symmetries of these levels. The nature of spontaneous symmetry breaking in the microcosm [23] [24] is similar to the nature of symmetry breaking in classical mechanics. The heterogeneity of the external fields of forces determines the symmetry breaking of the time.

7. Conclusions

In the framework of classical mechanics, all systems divided into two categories― 1) systems with holonomic constraints and 2) systems with nonholonomic constraints. This fact defines an obvious criterion to classify the types of nonlinearity.

So, there are fundamentally different types of nonlinearities that characterize the dynamics of the classical systems. The first type is nonlinearities that belong to the systems with holonomic constraints. The nonlinearities of the Hamiltonian systems belong to the first type of nonlinearities, since the requirement of holonomicity of the constraints is used in the derivation of Lagrange equation. Hamiltonian systems are reversible. For them, the volume of the phase space is preserved. The nonlinearities inherent to the Hamiltonian systems do not lead to evolution, because evolution is impossible without the dissipative processes.

Another type of nonlinearity, which we have called “evolutionary nonlinearities”, is only possible for systems with nonholonomic constraints. A distinctive feature of “evolutionary nonlinearity” is that the corresponding nonlinear terms depend on variables of different symmetry groups, which is connected with the different hierarchical levels of the body. In the classical mechanics, the “evolutionary nonlinearities” have a place when the system of MP is moving in a nonhomogeneous field of force. The presence of the gradient of field of force leads to engagement of the micro- and macro-variables defining the system dynamics and the dynamics of its internal structure. This leads to the transformation of the system motion energy into the internal energy. Thus, the “evolutionary nonlinearity” is inherent for the dissipative processes. They lead to the formation and development of structures accompanied by production of D-entropy in all hierarchical levels of the system. They determine the irreversibility of the system dynamics and violation of time symmetry.

The irreversibility of the dynamics of systems occurs when a sufficiently large number of MP in a system have a place. This is due to the fact that direct flow of energy into the system is determined by the non-linear terms of the second order, and the reverse flow of internal energy into kinetic energy of the system is determined by the terms of more than fourth order of smallness. With an increasing number of MP, the fluctuations of these flows decrease. Therefore, for sufficiently large numbers of MP, the value of the fluctuation of reverse flow energy not more than the value of the direct flow of energy

The condition of the infinite divisibility of matter implies that the bodies are represented by a number of embedded systems. Their dynamics are determined by the “evolutionary nonlinearities”, and by the hierarchical order, which corresponds to the degree of heterogeneity of the field of forces.

Dynamics systems are determined by the principle of dualism of symmetry at all hierarchical levels, as the work for any hierarchical level and on the change of its internal energy.

Cite this paper

Somsikov, V.M. (2017) Non-Linearity of Dynamics of the Non-Equilibrium Systems. World Journal of Mechanics, 7, 11-23. https://doi.org/10.4236/wjm.2017.72002

References