ABSTRACT

In this work we present a model for the determination of the interaction energy for triplet and singlet states in atoms with incomplete filled shells. Our model includes the modification of the Coulomb’s law by the interaction between the magnetic moments of the electrons. We find that the energy of the triplet state is lower than the energy of the singlet state. We calculate the interaction energy between the electrons from the adjacent atoms in fcc lattices and we find that the minimum interaction energy is attained for the triplet state. The result is presented for the interaction between the electrons of the first coordination group and those of the second coordination group. The interaction energy which aligns the spins is used to evaluate the Curie temperature in a mean field model.

1. Introduction

In condensed matter physics we are often interested on the importance that interactions between particles have on ground and excited states of the system and on its physical properties. To solve the many-body problem is a very difficult task and different methods and models are used which explain more or less accurate the physical effects that are measured. For example, magnetism in materials remains a very hot topic of research but the fundamental question of the magnetic order is based on the assumptions of the model used. Recent notable research in magnetism includes the nature of the ground state of an interacting two-dimensional (2D) electron gas in a magnetic field, as in quantum Hall effect and giant magnetoresistance [1- 4].

An important problem is that of the origin of ferromagnetism. The physical effect that produces magnetic ordering of adjacent magnetic moments is the same that leads to magnetic ordering within an ion and produces Hund’s rules. Interactions between spins are actually just a convenient way to record the end result of electrostatic repulsion [5]. Two electrons circling a nucleus reduce their Coulomb interaction by adopting an anti-symmetric wave function that vanishes whenever they come near each other. The Pauli principle demands that the overall wave function must be anti-symmetric, so the spin wave function must be symmetric. The electrons lower their energy by adopting the same spin state and developing a local magnetic moment. The important concepts were introduced by Heisenberg [6] and Stoner [7]. It was shown by Hubbard [8] that the correlation effects will lower the energy of non-magnetic states more than that of the ferromagnetic states and make the condition for ferromagnetism more stringent. The spin wave excitations give a way to explain the temperature dependence of the magnetization in magnetic materials at low temperatures [9].

In this paper, using an effective field Hamiltonian (detailed in [10]), we investigate the influence of the magnetic moments on the electron-electron interaction. We first discuss the modification of Coulomb’s law by the interaction between the magnetic moments of the electrons. Next, we present the case of an isolated atom with applications to Hund’s rules and the condition for ferromagnetism in fcc lattices.

2. Model and Formalism

In this section, we review the electron-electron interaction by using an effective field Hamiltonian [9] and extend the results to the case of the interaction between the magnetic moments of the electrons. The energy of the electron-electron interaction is given by the expression (see Appendix):

(1)

where D is a coupling constant, m is the mass of an electron, R is the distance between the two electrons, ρ_o is the massive density of the interacting field, DR/c² is the “massless density” of the interacting field, ω_q = cq is the classical oscillation frequency of the interacting field, 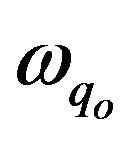is the oscillation frequency of an electron, q is the wave vector of the interacting field, q_o is the wave vector of the boson associated with the electron, k is the wave vector of the electron and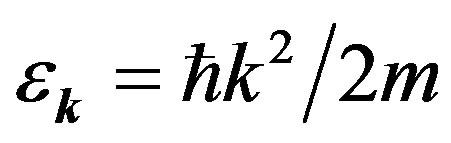, n_q is the occupation number of the bosons associated with the interacting field, is the occupation number of the bosons associated with the electrons, n_k is the occupation number for the electrons. When the interacting field is a photon field, then ρ_o = 0. For a quasi free electron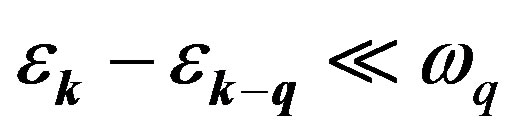, ( m is an effective electron mass) and by using that n_q, 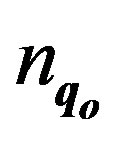= 0, n_k, n_k–q = 1, Equation (1) becomes:

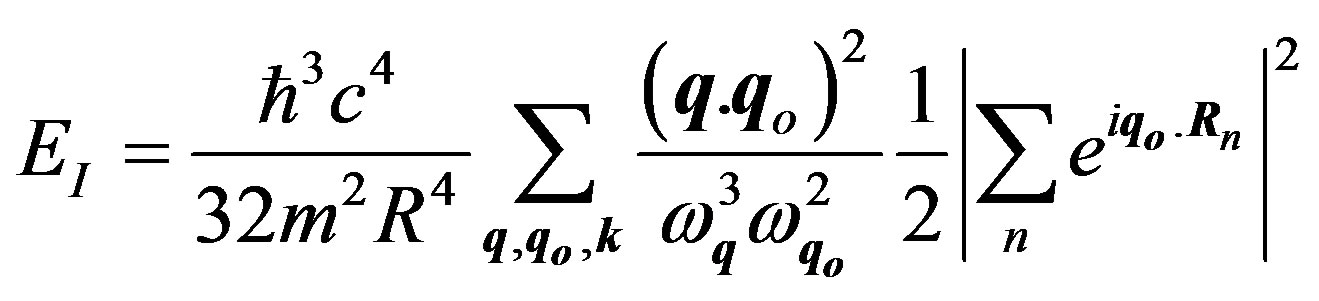(2)

To calculate Equation (2) we consider the two sums separately. The first sum can be easily calculated as:

and from the second one we obtain for q₁ = q₂ = q_o, R₂ – R₁ = R:

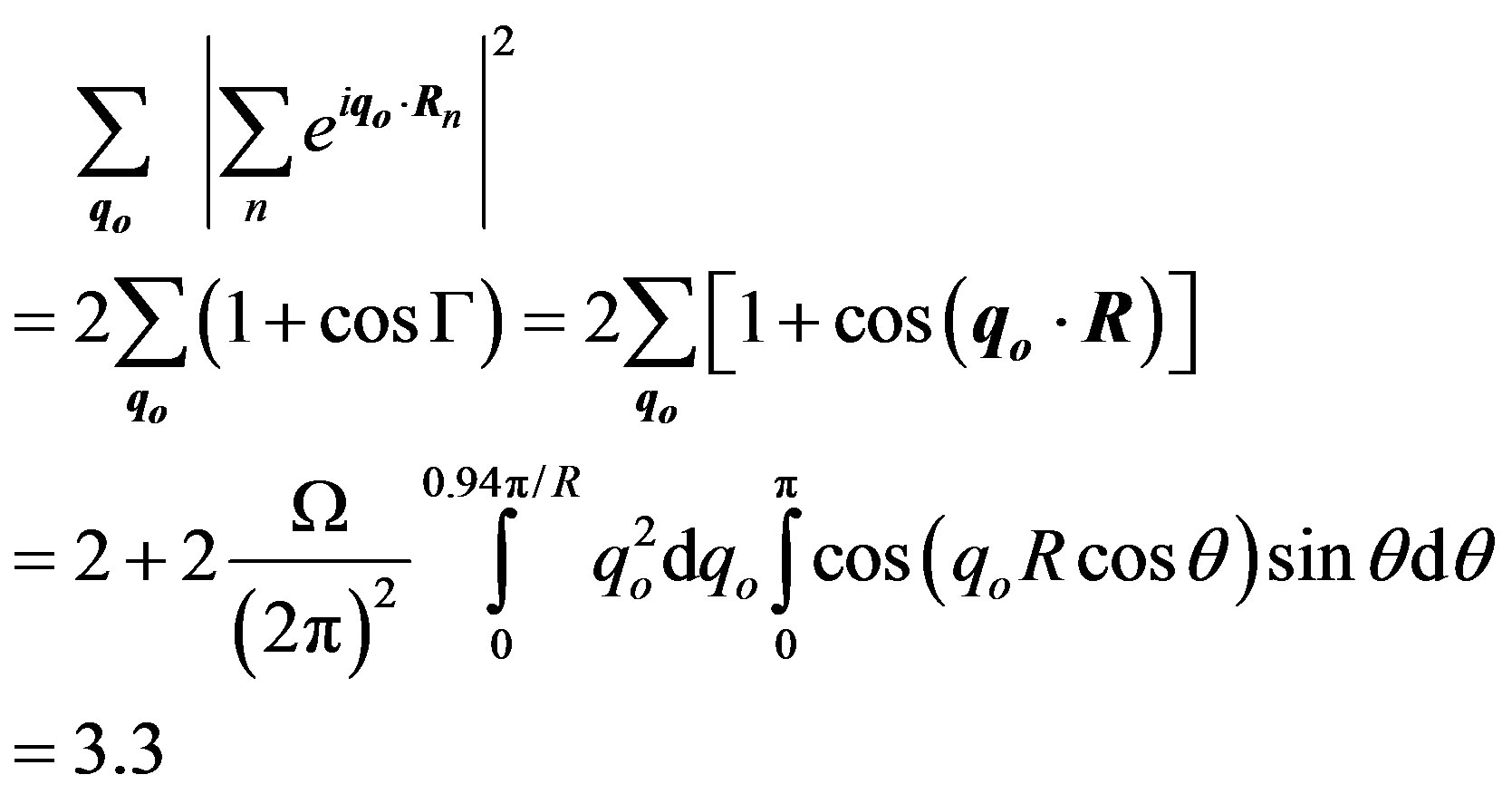(3)

where Γ = q₂ R₂ – q₁ R₁ for n = 1, 2.

The interaction energy becomes:

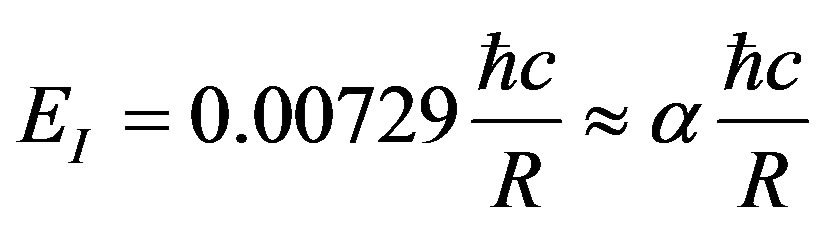(4)

Taking the upper limit of q_o as 0.94π/R, which is with 6% lower than π/R one obtains the value of α just as experimental value. The relation (4) represents the Coulomb’s law, which now is obtained without taken into account the electric charge concept. It can be shown [9] that for the charges of opposite sign the interaction energy (4) has the sign minus.

In presence of a magnetic field in the above equations we introduce the vector potential and thus we substitute q_o·r by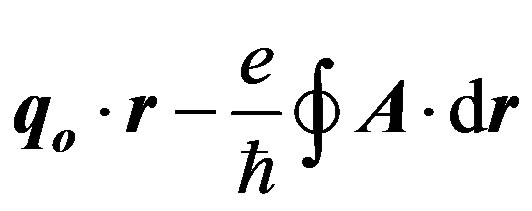. The second sum becomes: (See Equation (5), below).

The energy levels of atomic electrons are affected by the interaction between the electron spin magnetic moment and the orbital magnetic momentum of the electron. It can be visualized as a magnetic field caused by the electron’s orbital motion interacting with the spin magnetic moment. The effective magnetic field can be expressed in terms of the electron orbital angular momentum. We consider the vector potential where μ

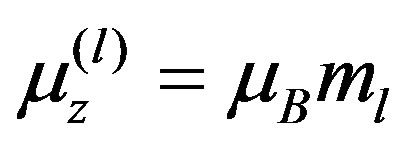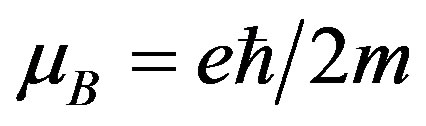is the magnetic dipole moment and r is a vector from the middle of the loop to an observation point. An electron in a stationary state in an atom, having a definite angular momentum projection L_z = ħm_l (m_l the quantum magnetic number), has a magnetic moment where is the Bohr magneton. 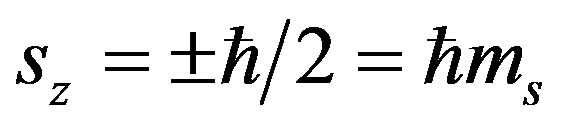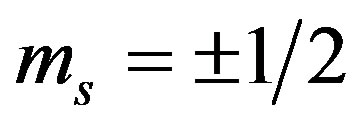The theory and experiments demonstrate that the free electron has a magnetic moment equal to the Bohr magneton μ_B, and a spin s, the projection of which on a specified direction are where is the spin quantum number. For 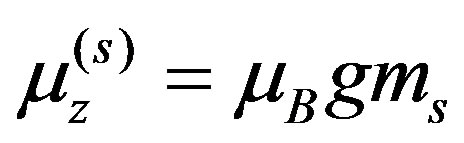with g = 2 we obtain:

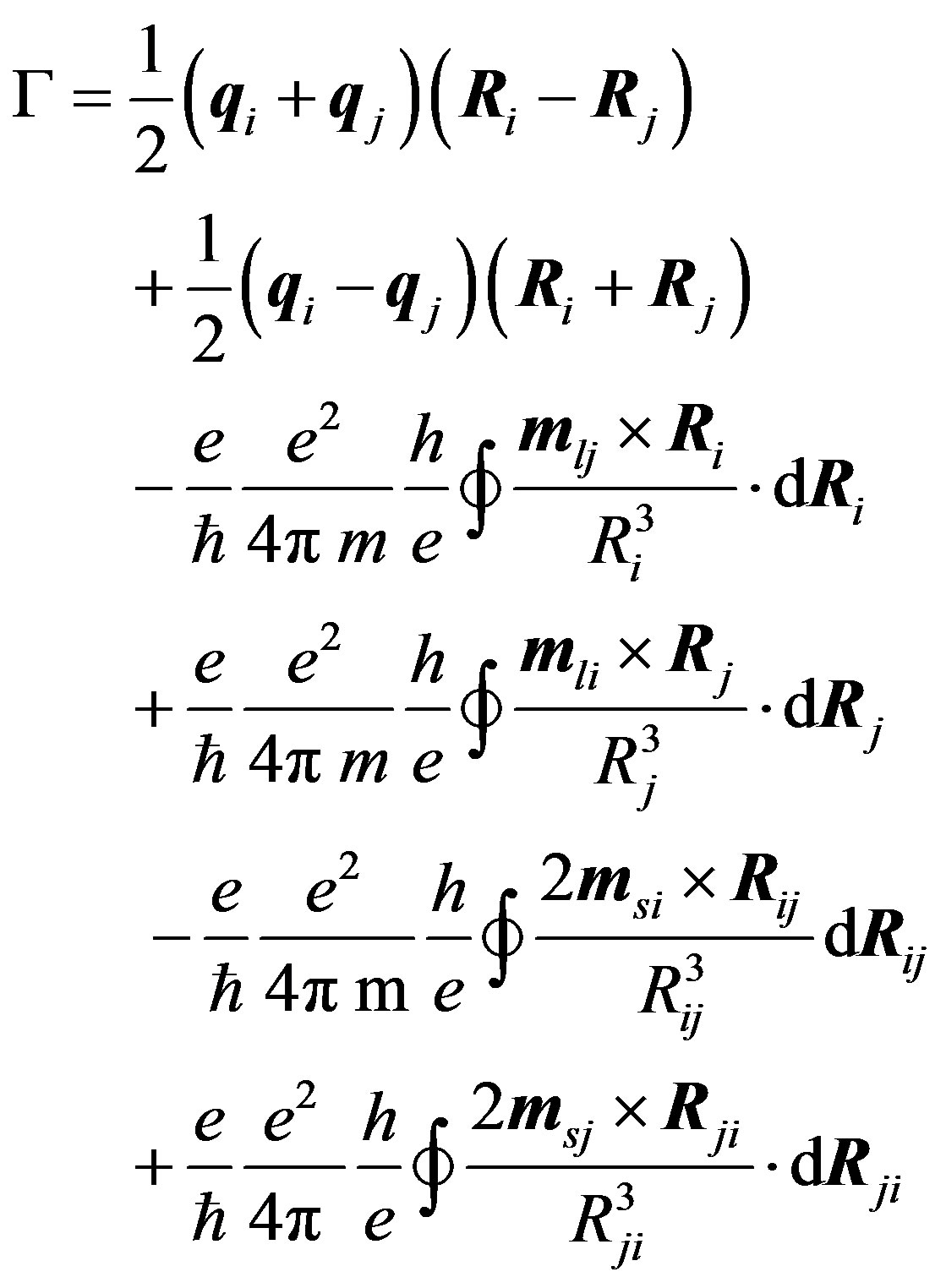
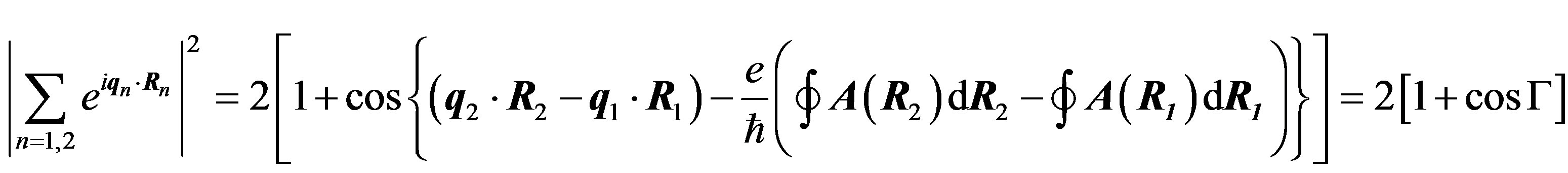(5)

where 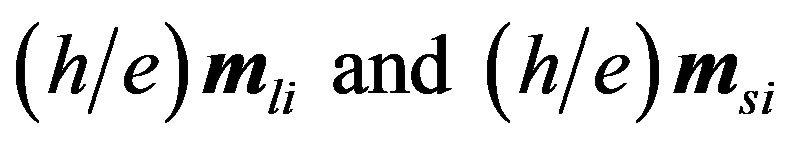are the flux vectors. For q_i = q_j =q_o:

In these conditions, where

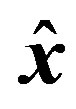is a unit vector perpendicular to R and μ. The interaction energy between two electrons, by taken into account their magnetic moments, becomes:

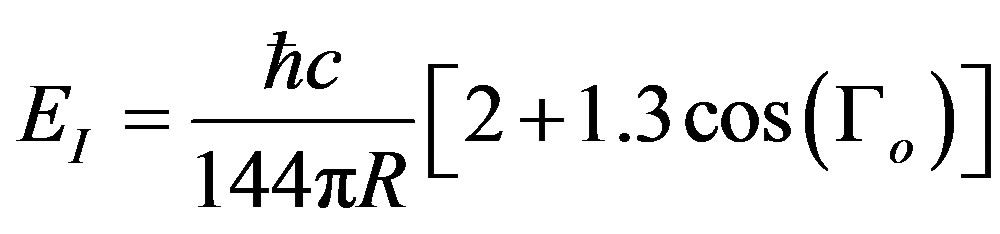(6)

For m_si = m_sj = 1/2, Γ_o reduces to:

(7a)

where R_o = R_i = R_j is the radius of the electron orbit and R = R_ij. For m_li – m_lj = 1, we obtain:

(7b)

For m_si = 1/2, m_sj = –1/2, we obtain:

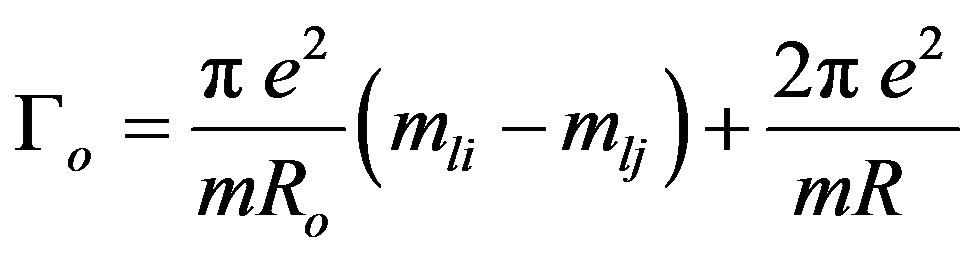(8)

For m_li = m_lj the above relation reduces to:

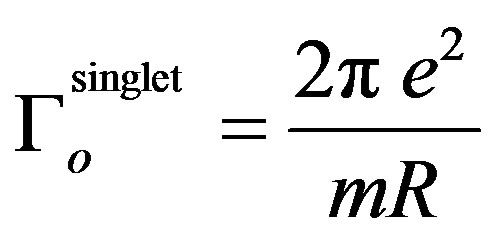(9)

For an average value of R equal to R_o, 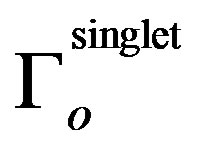= 2. In Figure 1, we plot, that is the difference between the function for the triplet state and the function for the singlet state. It is observed that for Γ_o = π the amplitude of this function has an absolute maximum, which is negative and therefore the interaction energy for the triplet state is lower than that associated with the singlet state. Thus for an atom with two valence electrons in a shell with l > 1, the interaction energy between the two electrons when they occupy different L_z states (all degenerate in energy) and adopt a triplet spin state, is smaller than the interaction energy when they occupy the same L_z state, in which case they must have opposite spins. Therefore, the triplet state is favorable. This may explain Hund’s rules related to the organization of electrons in incompletely filled shells.

3. Condition for Ferromagnetism

We consider an atom that has its total spin in the up direction. The intra-atomic interactions are of such a nature that this atom tends to attract electrons with spin up and repel those with spin down. In the case of the face-centered cubic lattice every atom is surrounded by 12 nearest neighbors, which have the coordinates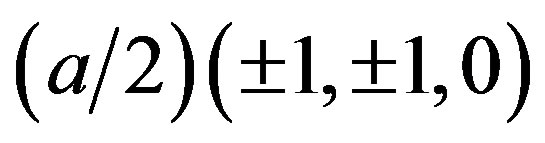,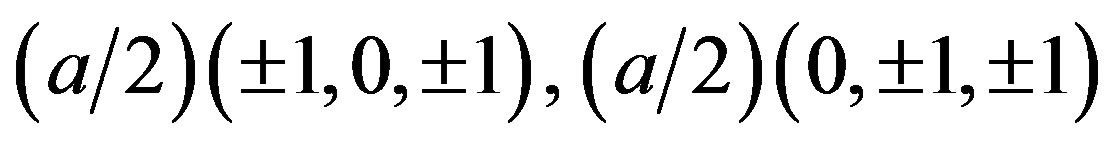. Suppose the magnetic moment μ(0, 0, μ). Then, the vector potential can be chosen in the following form A(A_x, A_y, 0). We obtain:

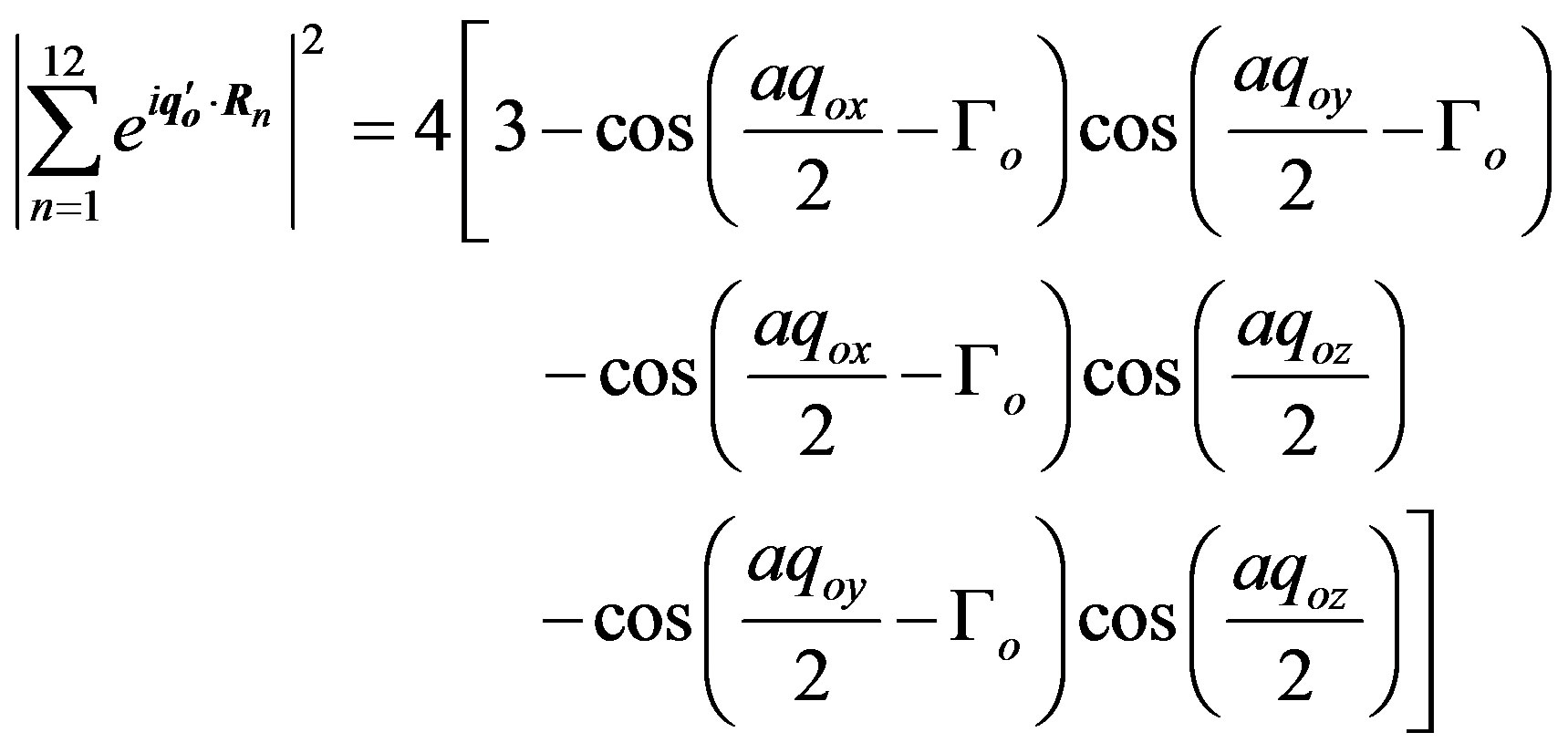(10)

where Γ_o is given by Equation (7b) for the triplet state and by Equation (9) for the singlet state. The sum in the interaction energy becomes:

(11)

with:

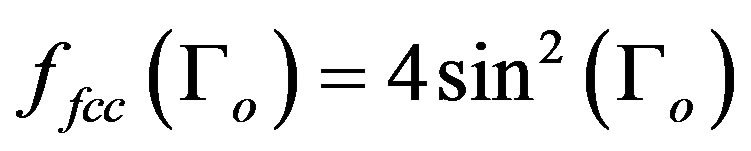(12)

The interaction energy becomes:

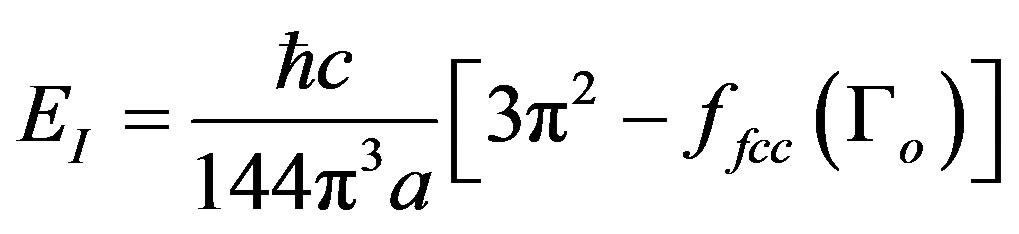(13)

From Equations (12) and (13), it appears that there is an oscillating interaction between the two electrons belonging to different atoms. The nature of this interaction may be not different of that which is encountered in the case of interaction between two ions by indirect exchange [11]. In the later case, the electrons belonging to an ion flip a conduction electron which then travels to another site and interacts with the spin of the ion of the second site. Perhaps the most significant application of the RKKY theory has been to the theory of giant magneto resistance (GMR) [3,4]. GMR was discovered when the coupling between thin layers of magnetic materials separated by a non-magnetic spacer material was found to oscillate between ferromagnetic and anti ferromagnetic as a function of the distance between the layers. The period of an oscillation is determined by the Fermi wave vector, in the case of free electron gas, via

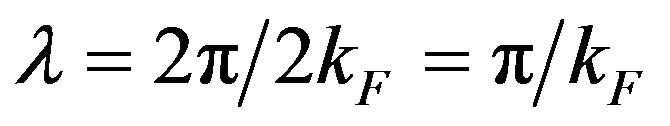. The phase of the cosine in RKKY theory is k_FR while in our theory this phase is 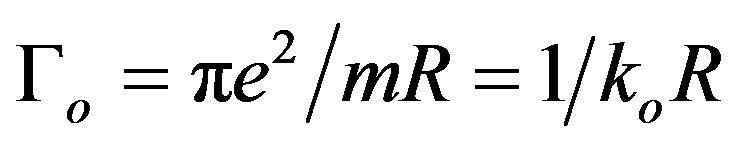where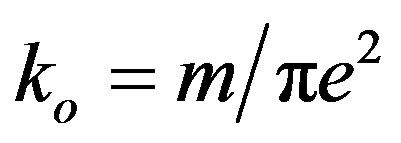. In this case the “period” of an oscillation is dependent of R. From the condition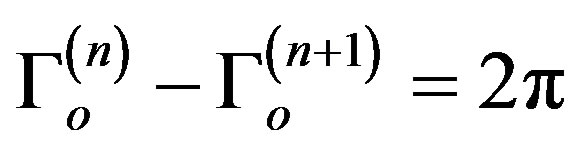, one obtains 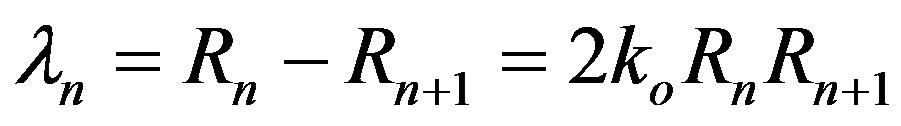The effective mass of the electron in d-band is larger than the free electron mass. For R_n ~ 3.3 Ǻ and m = 5m_o results λ_n ~ 0.4 Ǻ a value which is larger than the Compton wavelength, ħ/mc = 8 × 10^–3 Ǻ, and is lower than the period of the RKKY oscillation, which is of the order of 3 Ǻ. The oscillatory behaviour is the result of the interference of two oscillating fields generated by the magnetic moments of the two electrons. Each fringe arises from a definite difference in phase. The effect is an oscillatory polarization of the conduction electrons as it occurs in RKKY model.

In Figure 2, we show, that is the difference between the function f_fcc for the triplet state and the singlet state. It is observed that this function attains its absolute maximum at 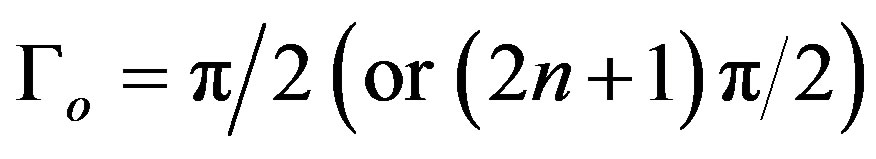and therefore the interaction energy between the two electrons for the triplet state is lower than that for the singlet state. The component of E_I which aligns the spins in the triplet state is:

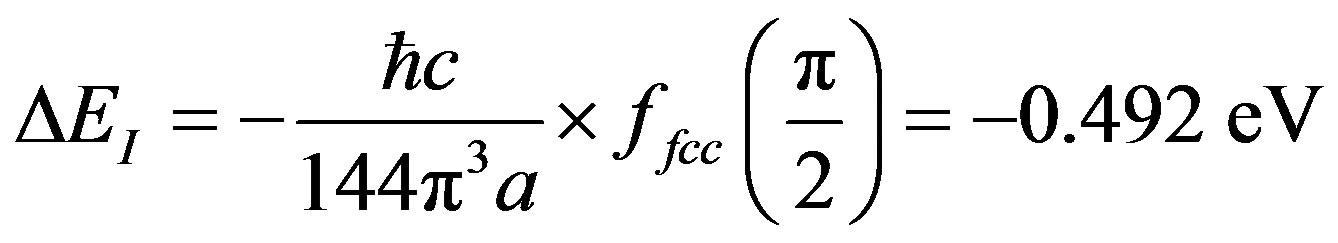
for a = 3.55 Ǻ. We must now take into account the screening effect due to the conduction electrons. The appropriate screening constant is κ₂ =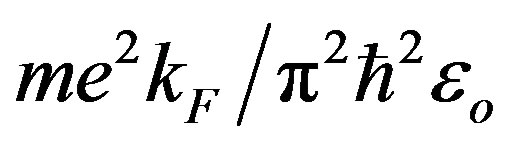, where the wave vector at the Fermi level is . In the Co fcc lattice, the density of electrons is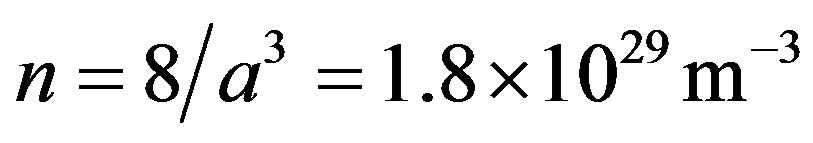. For the effective mass of the conduction electrons, m = 0.76 m_o, where m_o is the free electron mass, one obtains κ = 2.8 × 10⁹ m^–1. If we substitute in Equation (12) q'_os by q'_os + iκ (s = x, y, z) we obtain a multiplicative factor e^–κa (Yukawa form) to the above estimate ΔE_I reducing it to the order of magnitude –0.18 eV. The Curie temperature may be estimated as in the mean field theory applied to the spin-wave model [12,13]:

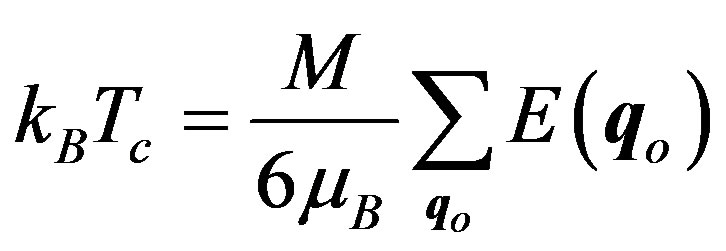
where M is the magnetic moment per atom, μ_B is the Bohr magneton, E(q_o) is the spin-wave energy which is related to the exchange parameter J_oj by a simple Fourier transformation:

Substituting the exchange parameter by our interaction parameter used in Equation (2), finally we obtain:

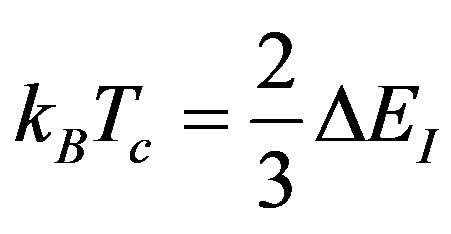
where ΔE_I is given by the above expression. For cobalt results T_c = 1411 K. A more elaborate method is the random phase approximation [12-14]. The Curie temperature can be also estimated numerically by employing the method of Monte Carlo simulations applied to effective Heisenberg Hamiltonian [15].

We take now into account the interaction with the atoms of the second group of coordination. If in a fcc structure we take into account the fact that every atom is surrounded by 6 neighbours of second order, which have the coordinates a(±1, 0, 0), a(0, ±1, 0), a(0, 0, ±1), then we must add to Equation (10) the term:

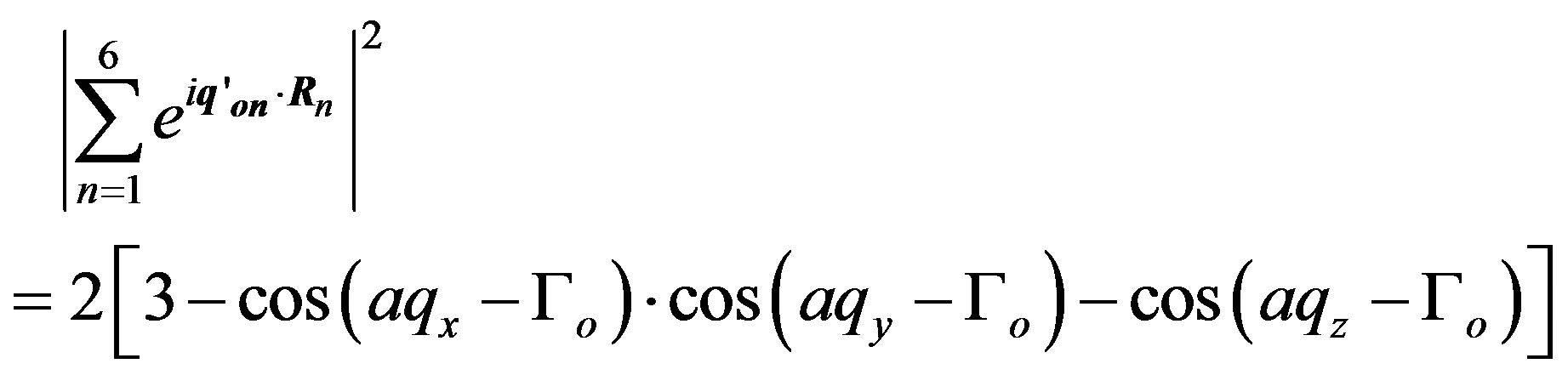
and the corresponding energy of interaction is:

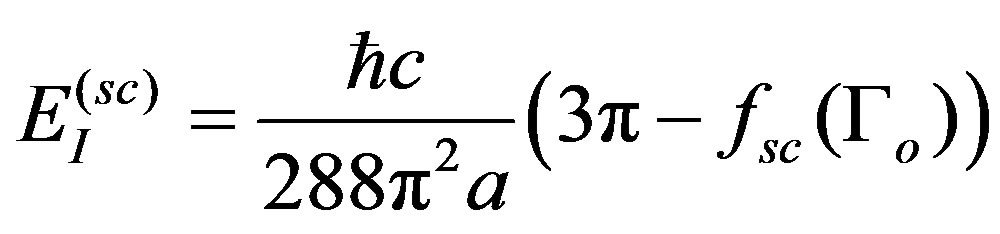(15)

with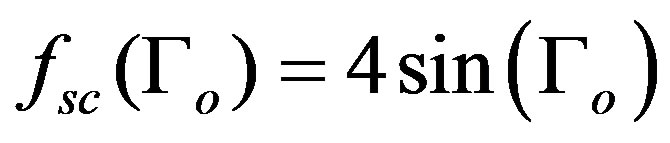

In Figure 3 Δf_sc = f_sc(Γ_o) – f_sc(2Γ_o) as a function of Γ_o is shown. It is observed that depending on the distance between the atoms the coupling may be ferromagnetic at Γ_o = 2.1 + 2sπ, as well as antiferromagnetic at 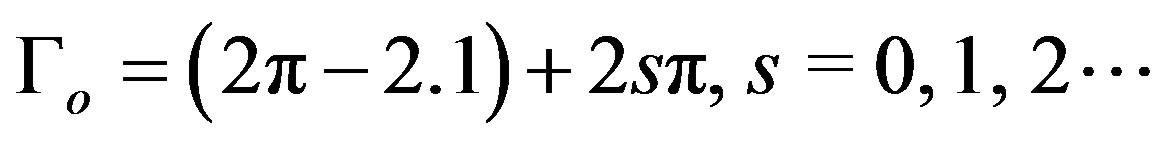This situation is also adequate for a simple cubic lattice. We note that in an fcc lattice of transition metals the ferromagnetic state is determined by the interaction between nearest neighbours.

4. Conclusion

Using an effective field Hamiltonian we have shown that the Coulomb’s law is modified by the spin-spin interaction. If we take into account the spin magnetic moment, when the spins are oriented antiparallel, the Coulomb interaction is modulated by a cosine term whose argument depends on the spin magnetic moment and on the distance between the two electrons. Evidently, this situation occurs in the absence of the magnetic field, for example in superconductors. Further, we have studied the influence of the electron magnetic moments, both orbital and spin, on the electron-electron interaction in an isolated atom. We have found that in an incomplete shell the interaction energy of the triplet state is smaller than the energy of the singlet state. On this basis may be explained Hund’s rules. The condition of ferromagnetism is studied in a fcc lattice of transition metals and the obtained results are in a good agreement with experimental data. By using the mean field approximation, we have estimated the Curie temperature. The coupling, due to the magnetic field generated by the two interacting electrons, oscillate with a “period” 1/k_oR where k_o = m/πe². This period of oscillation is dependent of R and for R = 3.3 Ǻ and m/m_o = 5, is equal to 0.4 Ǻ, a value which is smaller than the RKKY period of ~3 Ǻ. This means that the magnetic field generated by the magnetic moments of the electrons is modulated by an oscillation which has a period of π/k_F, where k_F is the Fermi wave vector.

REFERENCES

Appendix

The electron will always carry with it a lattice polarization field. The composite particle, electron plus phonon field, is called a polaron; it has a larger effective mass than the electron in the unperturbed lattice. By analogy, in our model, we consider a coupling between an electron and a boson.

Consider a linear chain of N bodies, separated at a distance R. The Hamiltonian operator of the interacting bodies (electrons) and the boson connecting field takes the general form:

where

is the Hamiltonian of the electrons of mass m, 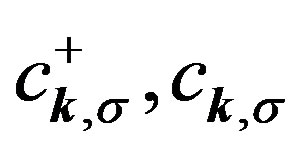are the electron creation and annihilation operators, k is the wave vector of an electron and σ is the spin quantum number,

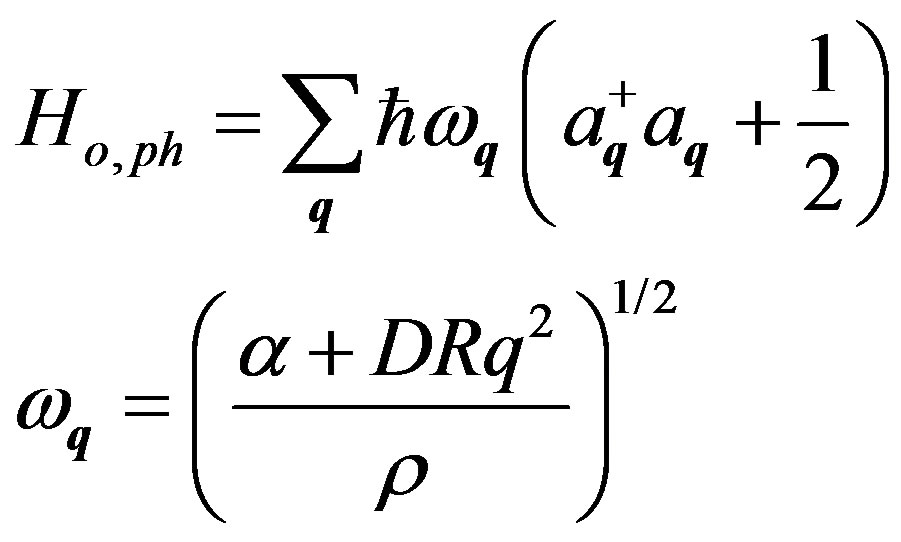
where 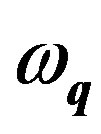is the classical oscillation frequency, α is the restoring force constant, D is the coupling constant, ρ is the linear density of flux lines, 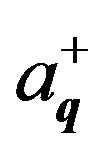, are the boson creation and annihilation operators and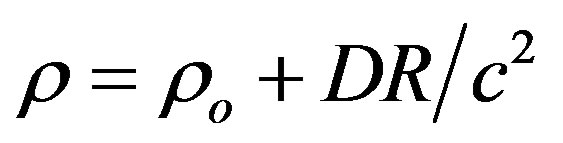, ρ_o is the density of the interacting field, if this is a massive field, c is the velocity of the boson waves. The interaction Hamiltonian operator H_I is given by the expression [16]:

where

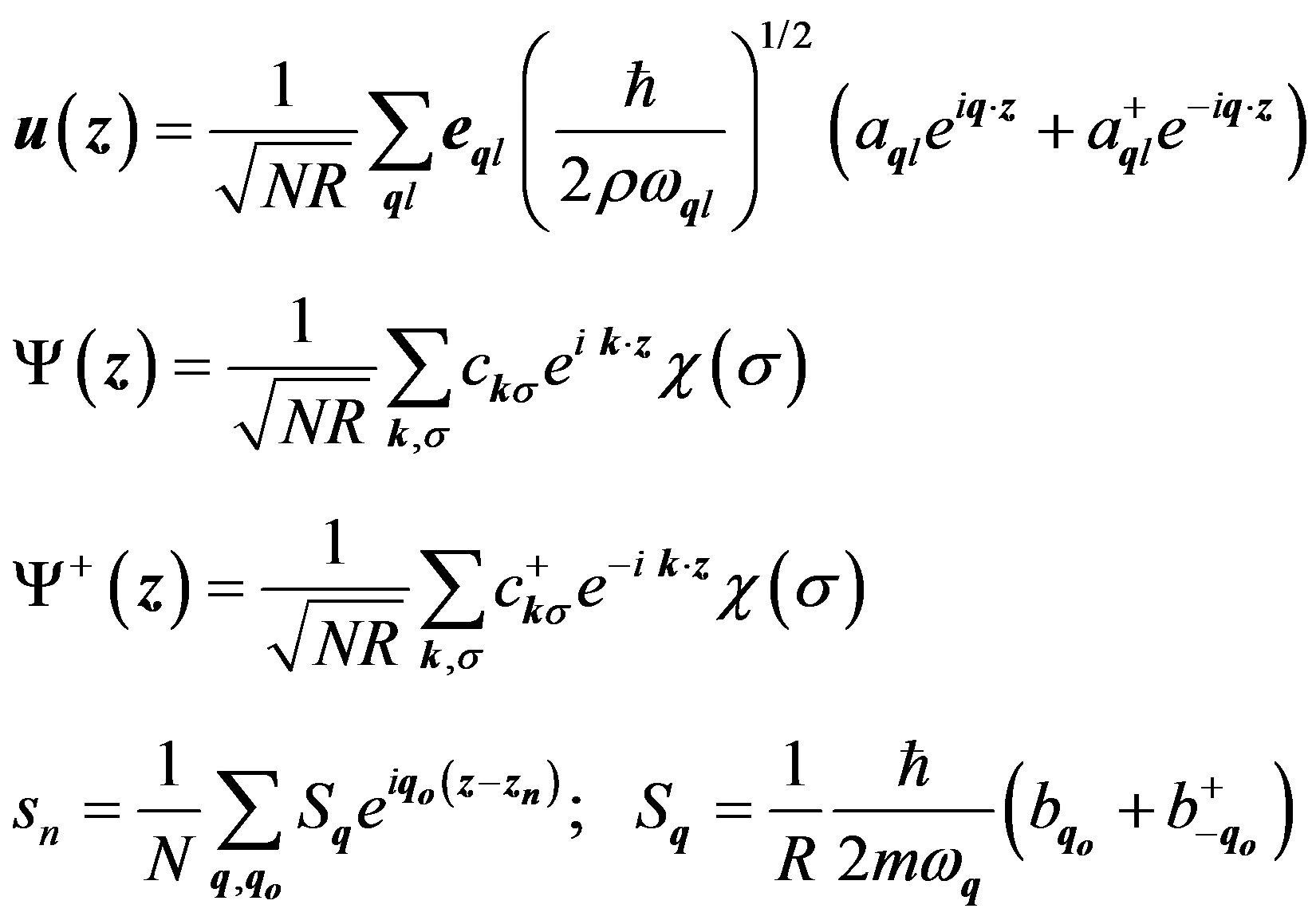
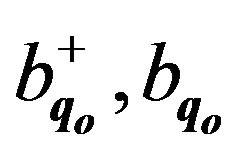are creation and annihilation operators associated with the electron oscillations, e_ql denotes the polarization vectors and χ(σ) is the spin wave function. s_n is the displacement of a body near its equilibrium position in the direction of R and, in the approximation of nearest neighbours, it is assumed that D does not depend on n. The Hamiltonian of interaction between electrons via bosons becomes:

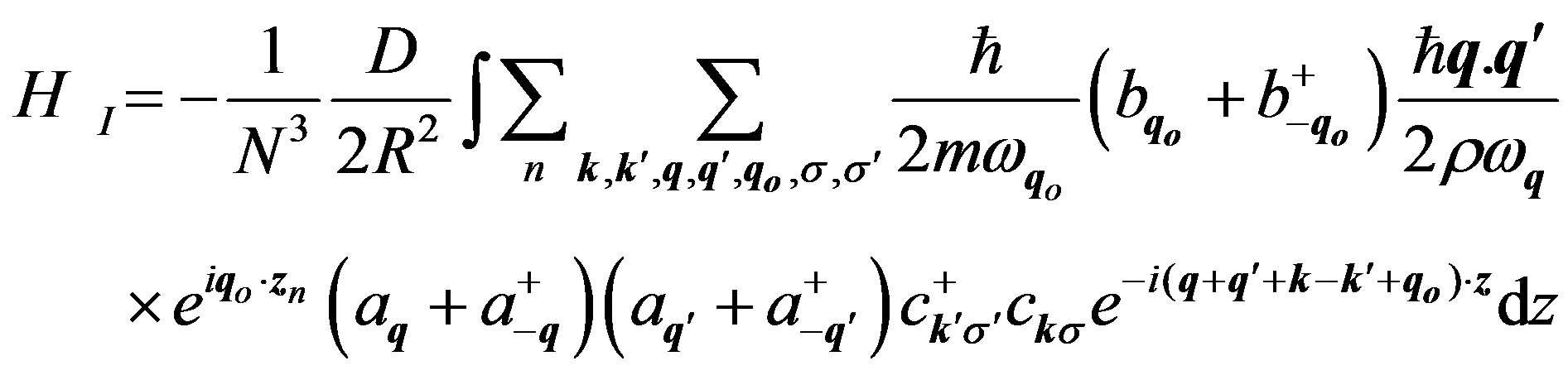
q, q' are the wave vectors associated with the bosons of the connecting field, q_o is the wave vector associated with the oscillations of the electron, and k, k' are the wave vectors of the electrons. Consider the integral over z:

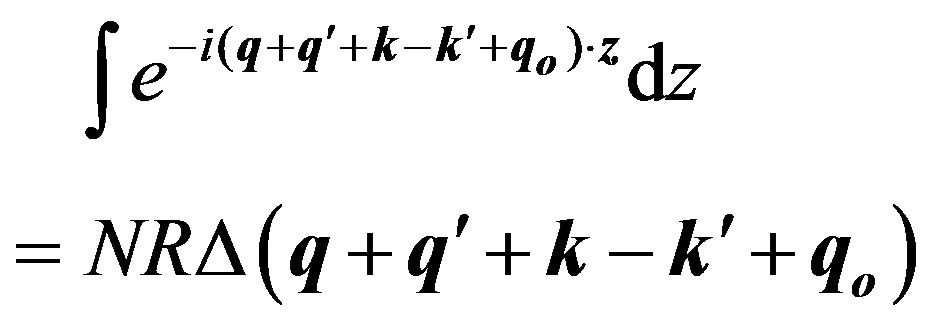(A1)

where Δ(x) = 1 for x = 0 and Δ(x) = 0, otherwise. In the bulk crystal NR is replaced by V = NΩ where Ω is the volume of a unit cell and N is the number of unit cells. We write:

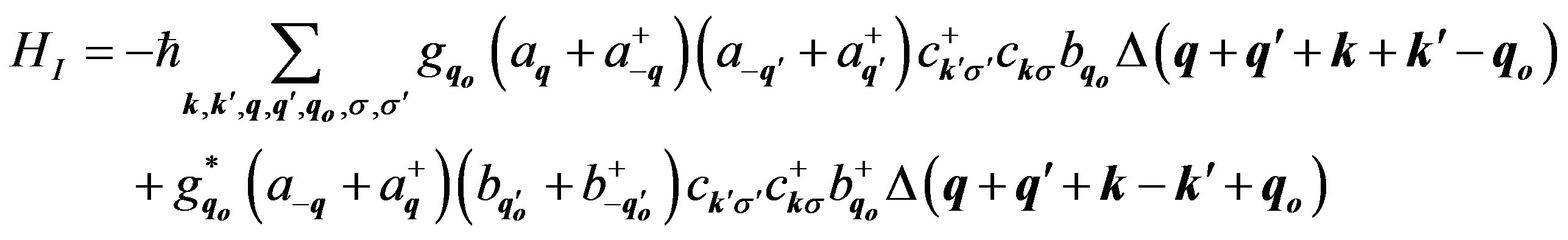
where

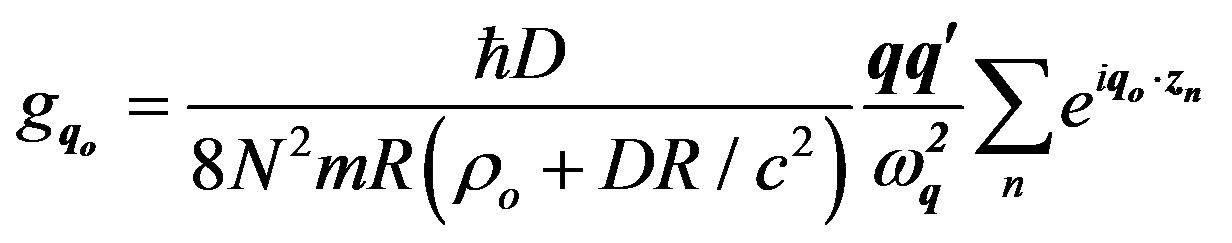
Approximating

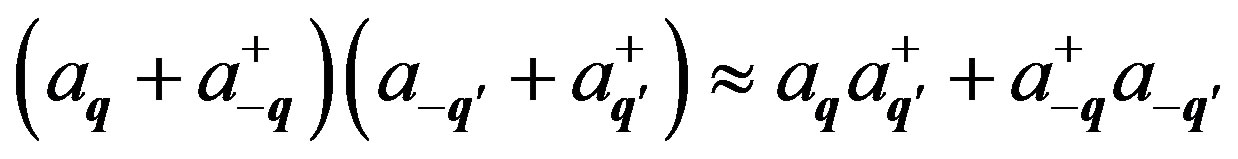
In Equation (A1) we choose q' =q_o, k' = k + q. In the interaction picture the effective Hamiltonian is given by:

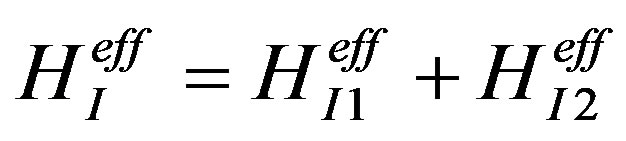
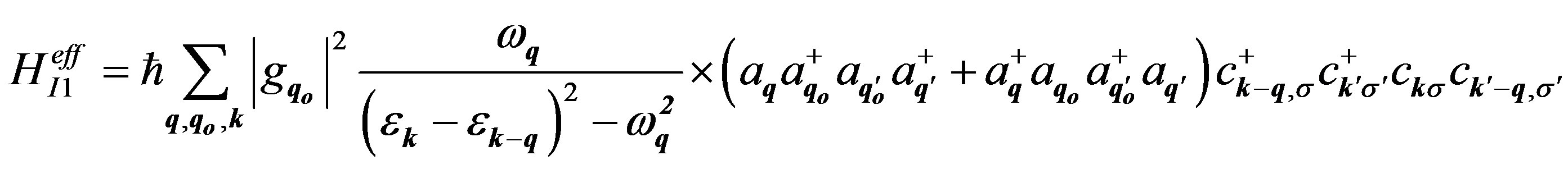
The expectation value of the energy of H_I1^eff is the energy of the electron-electron interaction given by Equation (1) in the text. The expectation value of the energy of H_I2^eff is the self energy of the electron and is used to calculate, for example, the polaron energy [10].

NOTES

^*Corresponding author.