International Journal of Astronomy and Astrophysics
Vol.07 No.01(2017), Article ID:73850,10 pages
10.4236/ijaa.2017.71001
Relativistic Variation of Black Hole Temperature with Respect to Velocity in XRBs and AGN
Dipo Mahto1, Alok Ranjan2, Krishna Murari Singh1
1Department of Physics, Marwari College, T. M. B. University, Bhagalpur, India
2Department of Physics, T. M. B. University, Bhagalpur, India

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: September 25, 2016; Accepted: January 22, 2017; Published: January 25, 2017
ABSTRACT
Stephen Hawking gave a formula for the temperature of black holes as given by (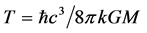 ). Some of the black holes have their spinning velocity from 50% to 99% of the velocity of light. Due to this velocity, the mass of black holes will vary which cause the variation in the temperature of black holes. In the present research article, we have applied the variation of mass with velocity
). Some of the black holes have their spinning velocity from 50% to 99% of the velocity of light. Due to this velocity, the mass of black holes will vary which cause the variation in the temperature of black holes. In the present research article, we have applied the variation of mass with velocity 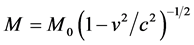 to obtain the rate of change in temperature of the black holes with respect to velocity. We have also calculated their values for super dense stars like black holes existing in XRBs and AGN and concluded that for super dense stars like black holes of lower velocity as well as the velocity comparable to the velocity of light, the rate of change in temperature with respect to velocity is directly proportional to their velocities. This work will help us to find out the variation in temperature of different black holes spinning with different velocity percentage related to light speed and can be used as the references for other research works.
to obtain the rate of change in temperature of the black holes with respect to velocity. We have also calculated their values for super dense stars like black holes existing in XRBs and AGN and concluded that for super dense stars like black holes of lower velocity as well as the velocity comparable to the velocity of light, the rate of change in temperature with respect to velocity is directly proportional to their velocities. This work will help us to find out the variation in temperature of different black holes spinning with different velocity percentage related to light speed and can be used as the references for other research works.
Keywords:
Hawking Temperature, Black Holes, XRBs, AGN

1. Introduction
In classical theory, black holes can only absorb and not emit particles. However, it is shown that quantum mechanical effects cause black holes to create and emit particles like a black body [1] [2] . But according to general theory of relativity, a black hole is a solution of Einstein’s gravitational field equations in the absence of matter that describes the space time around a gravitationally collapsed star and its gravitational pull is so strong that even light cannot escape from it [3] .
In 1974, Hawking discovered black hole evaporation. Quantum fields on a black hole background space-time radiate thermal spectrum of particles, with a temperature (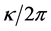 ), where
), where 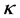 is the surface gravity of the horizon [1] . Hawking (1974, 1975) introduced what is now called Hawking radiation as the effective black body radiation from a black hole in terms of the 4th power of the black hole temperature and the Stefan-Boltzmann constant [4] [5] . Stephan Hawking provided a theoretical argument for its existence in 1974, and sometimes also after the physicist Jacob Bekenstein who predicted that black holes should have a finite, non-zero temperature and entropy and also stated that it is proportional to the black hole area A [6] . Bardeen, Carter and Hawking performed calculations using a semi-classical approximation, putting Bekenstein conjecture on a firm basis. They established that the black hole temperature is proportional to its surface gravity [7] . The surface gravity has the same role in black hole thermodynamics as the temperature in the ordinary thermodynamics. Silva proposed intuitive derivations of the Hawking temperature and the Bekenstein-Hawking entropy of a Schwarzschild black hole [8] . Ved Prakash et al. have discussed the statistical analysis of lifetime and temperature of the black holes existing in X-ray binaries and active galactic nuclei [9] . Mehta et al. derived an expression for the variation of temperature of the black holes with respect to mass and also calculated their values of different test black holes existing only in X-ray binaries [10] . Mahto et al. converted the Hawking temperature in terms of Chandrasekhar limit (Mch) and calculated their values for different test black holes in XRBs and AGN [11] . In the present research work, we have applied the variation of mass with velocity as proposed by Albert Einstein to the Hawking temperature (
is the surface gravity of the horizon [1] . Hawking (1974, 1975) introduced what is now called Hawking radiation as the effective black body radiation from a black hole in terms of the 4th power of the black hole temperature and the Stefan-Boltzmann constant [4] [5] . Stephan Hawking provided a theoretical argument for its existence in 1974, and sometimes also after the physicist Jacob Bekenstein who predicted that black holes should have a finite, non-zero temperature and entropy and also stated that it is proportional to the black hole area A [6] . Bardeen, Carter and Hawking performed calculations using a semi-classical approximation, putting Bekenstein conjecture on a firm basis. They established that the black hole temperature is proportional to its surface gravity [7] . The surface gravity has the same role in black hole thermodynamics as the temperature in the ordinary thermodynamics. Silva proposed intuitive derivations of the Hawking temperature and the Bekenstein-Hawking entropy of a Schwarzschild black hole [8] . Ved Prakash et al. have discussed the statistical analysis of lifetime and temperature of the black holes existing in X-ray binaries and active galactic nuclei [9] . Mehta et al. derived an expression for the variation of temperature of the black holes with respect to mass and also calculated their values of different test black holes existing only in X-ray binaries [10] . Mahto et al. converted the Hawking temperature in terms of Chandrasekhar limit (Mch) and calculated their values for different test black holes in XRBs and AGN [11] . In the present research work, we have applied the variation of mass with velocity as proposed by Albert Einstein to the Hawking temperature (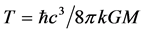 ), where
), where 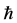 is the reduced Planck constant, c is the speed of light,
is the reduced Planck constant, c is the speed of light, 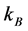 is the Boltzmann constant, G is the gravitational constant, and M is the mass of the black hole, to obtain the rate of change in temperature with respect to velocity and also calculated their values for super dense stars like black holes existing in XRBs & AGN.
is the Boltzmann constant, G is the gravitational constant, and M is the mass of the black hole, to obtain the rate of change in temperature with respect to velocity and also calculated their values for super dense stars like black holes existing in XRBs & AGN.
2. Method
Zee presented a nice intuitive derivation of the Hawking temperature on the basis of Schwarzschild solution of Einstein equations for vacuum in his book entitled: Quantum field Theory in a Nutshell [12] as given below.
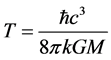 (1)
(1)
The above equation for the temperature of black holes was Stephan Hawking’s discovery in 1974, showing that the temperature associated with black holes is inversely proportional to their mass as follows:
 (2)
(2)
With using  in natural units, Equation (2) immediately implies that a Schwarzschild black hole in isolation is unstable: it will radiate and so doing loss energy, hence the mass decreases, thus increasing the temperature causing it to radiate with more power leading to runway effect [13] .
in natural units, Equation (2) immediately implies that a Schwarzschild black hole in isolation is unstable: it will radiate and so doing loss energy, hence the mass decreases, thus increasing the temperature causing it to radiate with more power leading to runway effect [13] .
Equation (2) can be written as
 (3)
(3)
Some of the black holes have their spinning velocity from 50% to 99% of the velocity of light [14] and hence the mass of black holes do not remain constant, but the mass will vary with velocity as proposed by Albert Einstein’s special theory of relativity as [15] :
 (4)
(4)
where  is the rest mass and v be the spinning velocity of black holes.
is the rest mass and v be the spinning velocity of black holes.
or, (5)
(5)
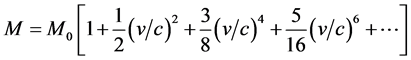 (6)
(6)
Since, 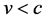 , hence
, hence
 ,
, 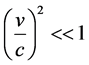 ,
, 

Hence, it is clear that the terms of higher power of 

Putting the value of M in Equation (3), we have

or

The terms containing Equation (10) have positive and negative contributions, so the resultant value of the terms in big bracket will be negligible. Also applying the condition of Equation (7), the higher power of 

Equation (11) may be designated as Relativistic Hawking temperature of the black holes which is less than Hawking temperature of the black holes. This means that the temperature of black hole decreases with the increase the velocity of black holes. The simplest form of Equation (11) may be written to assume for convenience

The relativistic temperature of different black holes can be calculated with the help of Equation (12) for known rest mass and spinning velocity of the black holes. To obtain the rate of variation of the temperature of the black holes relative to velocity, Equation (12) is differentiated with respect to v.

or,

so that

The above equation shows that for super dense stars like black holes of lower velocity as well as the velocity comparable to the velocity of light, the magnitude of rate of change in temperature with respect to velocity is directly proportional to spinning velocity of black hole.
3. Data in Support of Spinning Velocity of Black Holes
E.S. Reich demonstrated graphically in his research work that the spinning rate of the super massive black holes begin from about 50% of the speed of light to 99% of the speed of light and there are some super massive black holes spinning at more than 90% of the speed of light. The graph also shows that no super massive black holes spin at rate below than 40% of the speed of light [14] . From above it is clear that the super massive black holes existing in AGN have spinning rate from about 50% to 99% of the velocity of light and the massive black holes existing in XRBs may have spinning rate from about 1% to 99% of the velocity of light.
4. Data in Support of Mass of Black Holes
There are two categories of black holes classified on the basis of their masses clearly very distinct from each other, with very different masses M ~ 5 20 



5. Results and Discussion
A black hole has a temperature which is inversely proportional to the mass of black holes as per Hawking temperature formula. A body having mass with a finite temperature radiates energy. Anything that radiates energy is also losing mass according to Einstein’s mass-energy equivalence relation (E = mc2). Looking at the equation, we can see that as the black hole loses mass, the emission of energy from the black hole increases and its temperature increases, and thus the rate of mass loss increases.
In the present work, we have applied the variation of mass with velocity to the Hawking temperature and derived an expression for the relativistic Hawking temperature given by Equation (12). With the help of Equation (12), the rate of change in temperature of black holes with respect to the spinning velocity is obtained by Equation (13). We also calculated their values with the help of Equation (13) for different masses of different massive, 5







Table 1. The rate of change of temperature of black holes w.r.t. spinning velocity in XRBs.
Table 2. The rate of change of temperature of black holes w.r.t. spinning velocity in AGN.
Figure 1. The graph plotted between % spinning velocity of black holes of velocity of light and the rate of change of temperature of black holes w.r.t. spinning velocity for mass M = 5 
Figure 2. The graph plotted between % spinning velocity of black holes of velocity of light and the rate of change of temperature of black holes w.r.t. spinning velocity for mass M = 10 
Figure 3. The graph plotted between % spinning velocity of black holes of velocity of light and the rate of change of temperature of black holes w.r.t. spinning velocity for mass M = 15 
Figure 4. The graph plotted between % spinning velocity of black holes of velocity of light and the rate of change of temperature of black holes w.r.t. spinning velocity for mass M = 20 
Figure 5. The graph plotted between % spinning velocity of black holes of velocity of light and the rate of change of temperature of black holes w.r.t. spinning velocity for mass M = 106 
Figure 6. The graph plotted between % spinning velocity of black holes of velocity of light and the rate of change of temperature of black holes w.r.t. spinning velocity for mass M = 107 
Figure 7. The graph plotted between % spinning velocity of black holes of velocity of light and the rate of change of temperature of black holes w.r.t. spinning velocity for mass M = 108 
Figure 8. The graph plotted between % spinning velocity of black holes of velocity of light and the rate of change of temperature of black holes w.r.t. spinning velocity for mass M = 109 
with the help of Table 2. When we observe the graphs plotted in Figures 1-8, we see that all the graphs are straight lines which show that there are uniform variation of the rate of change of temperature of black holes w.r.t. spinning velocity (



6. Conclusions
In the study of present research paper, we conclude that:
1) The relativistic Hawking temperature of the black hole is less than to that of Hawking temperature.
2) The black hole of lower velocity as well as the velocity comparable to the velocity of light, the rate of change in temperature with respect to velocity is directly proportional to its spinning velocity.
3) All the graphs between % spinning velocity of black holes of velocity of light and the rate of change of temperature of black holes w.r.t. spinning velocity for different masses of black holes either for XRBs or AGN are in straight line showing that there is a definite relation and uniform variation between the rate of change in temperature with respect to velocity and spinning velocity.
4) The straight line graph gives the validity of relation between the rate of change in temperature with respect to velocity and its spinning velocity.
Acknowledgements
Authors are highly grateful and obliged to the reviewers specially Najat M.R. Al- Ubaidi who made some excellent unbelievable corrections and editors for pointing out the technical errors in the original manuscript and providing valuable suggestions to make it better.
Cite this paper
Mahto, D., Ranjan, A. and Singh, K.M. (2017) Relativistic Variation of Black Hole Temperature with Re- spect to Velocity in XRBs and AGN. International Journal of Astronomy and Astrophysics, 7, 1-10. https://doi.org/10.4236/ijaa.2017.71001
References
- 1. Wald, R.M. (2001) The Thermodynamics of Black Holes. Living Reviews in Relativity, 4, 6.
https://doi.org/10.12942/lrr-2001-6 - 2. Mahto, D., Prakash, V., Singh, B.K. and Singh, K.M. (2012) Change in Entropy of Non-Spinning Black Holes w.r.t. the Radius of Event Horizon in XRBs. Astrophysics and Space Science, 343, 153-159.
https://doi.org/10.1007/s10509-012-1219-y - 3. Dabholkar, A. (2005) Black Hole Entropy in String Theory—A Window into the Quantum Structure of Gravity. Current Science, 89, 25.
- 4. Hawking, S.W. (1975) Particle Creation by Black Holes. Communications in Mathematical Physic, 43, 199-220.
https://doi.org/10.1007/BF02345020 - 5. Hawking, S.W. (1974) Black Hole Explosions? Nature, 248, 30-31.
https://doi.org/10.1038/248030a0 - 6. Hawking, S.W. (1988) A Brief History of Time. Bantam Books, New York.
- 7. Bardeen, J.M., Carter, B. and Hawking, S.W. (1973) The Four Laws of Black Hole Mechanics. Communications in Mathematical Physics, 31, 161-170.
https://doi.org/10.1007/BF01645742 - 8. Mehta, R.N., Prasad, U., Kumar, A. and Mahto, D. (2013) Study of Variation of Temperature of Black Holes with Respect to Mass in XRBs. International Journal of Astrophysics and Space Science , 1, 61-63.
https://doi.org/10.11648/j.ijass.20130104.18 - 9. Silva, P.R. (2006) A Note on Black Hole Temperature and Entropy. General Relativity and Quantum Cosmology. arXiv.org/pdf/gr-qc/0605051
- 10. Prakash, V., Mahto, D., Kumar, V. and Das, B.K. (2013) Statistical Analysis of Life-Time and Temperature of Black Holes. American Journal of Theoretical and Applied Statistics, 2, 228-232.
https://doi.org/10.11648/j.ajtas.20130206.20 - 11. Mahto, D., Jha, B.K., Singh, K.M. and Ram, M. (2015) Study of Temperature of Black Holes in Terms of Chandrasekhar Limit. International Letters of Chemistry, Physics and Astronomy, 40, 43-50.
https://doi.org/10.18052/www.scipress.com/ILCPA.40.43 - 12. Zee, A. (2003) Quantum Field Theory in a Nutshell. Princeton University Press, Princeton.
- 13. Dolan, B.P. (2012) Where Is the PdV Term in the First Law of Black-Hole Thermodynamics? 9th Vienna Central European Seminar on Particle Physics and Quantum Field Theory, Vienna, 30 November-2 December 2012, 1-13.
- 14. Reich, E.S. (2013) Spin Rate of Black Holes Pinned Down. Nature, 500, 135.
https://doi.org/10.1038/500135a - 15. Bergmann, P.G. (1969) Introduction to the Theory of Relativity. Prentice-Hall of India, New Delhi.
- 16. Narayan, R. (2005) Black Holes in Astrophysics. New Journal Physics, 7, 1-31.
https://doi.org/10.1088/1367-2630/7/1/199 - 17. Mahto, D., Nadeem, M.S., Prasad, U., Kumar, A. and Singh, K.M. (2013) Change in Entropy of Non-Spinning Black Holes w.r.t. the Radius of Event Horizon in AGN. Journal of Modern Physics, 4, 321-326.
https://doi.org/10.4236/jmp.2013.43043 - 18. Madejski, G. (2003) Black Holes in Active Galactic Nuclei. SLAC-PUB-9702.
https://doi.org/10.2172/812998 - 19. Sargent, W.L.W. (1978) Dynamical Evidence for a Central Mass Concentration in the Galaxy M87. The Astrophysical Journal, 221, 731-744.
https://doi.org/10.1086/156077 - 20. Ferrarese, L. and Ford, H. (2005) Super Massive Black Holes in Galactic Nuclei: Past Present & Future Research. Space Science Reviews, 116, 523-624.
https://doi.org/10.1007/s11214-005-3947-6 - 21. Blandford, R.D. (1999) Recent Results on Active Galactic Nuclei. Astrophysics and Space Science, 261, 245-252.
https://doi.org/10.1023/A:1002093710287










