Received 25 June 2015; accepted 24 August 2015; published 27 August 2015

ABSTRACT

We review here the recent success in modeling our expanding universe according to the rules of flat space cosmology. Given only a few basic and reasonable assumptions and a single observational input, our model derives a variety of results which correlate with astronomical observations, including best estimates of the size, total mass, temperature, age and expansion rate of our observable universe. Considering the apparent success of our model, we attempt to explain why we think it works so well, including the fact that it incorporates elements of both general relativity and quantum mechanics. We offer this approach as a possible avenue towards understanding cosmology at the quantum level (“quantum gravity”).

Keywords:

Flat space Cosmology, Hubble Parameter, Hubble Radius, CMBR Redshift, Schwarzschild Formula, Hawking Black Hole Temperature Formula, Quantum Gravity

1. Introduction

Flat space cosmology is our newly introduced heuristic model of cosmology [1] [2] . Relying on only a few basic and reasonable assumptions, it has allowed us to derive a variety of numbers in close agreement with astrono- mical observations, including 2015 Planck survey results [3] . In our introductory paper [1] , we derived Hubble parameter H₀, Hubble radius R₀, Hubble time H_T and total mass M₀ values for our current observable universe relying only on our basic assumptions and current CMB radiation temperature T₀ = 2.725 K. In the follow-up paper [2] , we derived current Hubble radius R₀, Hubble time H_T (universal age), total mass M₀, cosmic temperature T₀ and CMBR redshift, knowing only the current Hubble parameter H₀ value of 68.6 km/sec/Mpc (2015 Planck survey upper limit). In this paper, we summarize the key mathematical relationships and attempt to explain why such a simple model works so well.

2. Our Key Model Assumptions

Our key model assumptions can be expressed as follows, for any scale from the Planck scale to the scale of our observable universe:

1) Cosmic radius 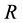and total mass 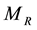follow the Schwarzschild formula 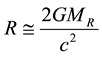at all times.

2) The cosmic event horizon always translates at speed of light c with respect to its geometric center. Thus, in our model, the Hubble parameter H_R can be expressed as c/R. And considering assumptions 1 and 2 together, the

cosmic Hubble radius can be expressed as 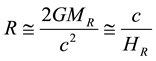and Hubble time (universal age) can be expressed

as 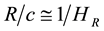for any stage of cosmic expansion.

3) The possible range of cosmic linear velocity of rotation at the Planck scale can be assumed to be anywhere from zero up to the special relativity limit of c. If we start by assuming the maximum possible value (c), then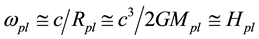, where 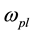is the Planck scale angular velocity, 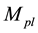is the Planck mass, is the Planck scale Hubble parameter and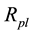_, according to assumption 1, is the Planck radius and equals twice the

Planck length. As such,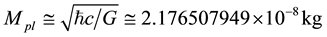 , and,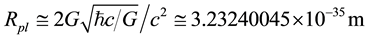

and the Planck scale Hubble parameter 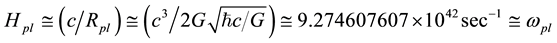in rad・sec⁻¹.

4) Following thermodynamics of Hawking’s black hole temperature formula [4] , at any radius 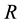cosmic temperature 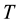is inversely proportional to the geometric mean of cosmic total mass M_R and the Planck mass.

(1)

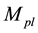3. Our Model Formulae Based on These Assumptions

3.1. Relations between Cosmic Radius, Total Mass and Hubble Parameter

(2)

(3)

where, and represent cosmic radius, total mass and Hubble parameter, respectively. Average mass density equaling Friedmann’s critical density is seen in the second line. Hence, our cosmic model is constantly “flat” by the Friedmann formula.

3.2. Relations between Temperature, Mass, Radius and Hubble Parameter (Thermodynamics)

(4)

(5)

(6)

(7)

where T_R represents the cosmic temperature for a given cosmic radius R.

4. Our Derivations of Current Cosmological Parameters

Using only our basic assumptions and the equations they generate above, derivations of current values for our observable universe are as follows:

Relations between universal current radius R₀, current temperature T₀, current Hubble parameter H₀, current total mass M₀, and current average mass density:

(8)

(9)

(10)

(11)

where is the average mass density and is Friedmann’s critical average mass density.

The above-derived radius and mass values simulate a current observable universe with a radius of 14.6 billion light-years and roughly 2 × 10²² visible stars plus 5 × dark matter, roughly 10⁵³ kg.

Derived current cosmological values are consistent with 2015 Planck survey data. As per the 2015 Planck survey data, the current value of the Hubble parameter is reported to be:

As per the 2015 Planck data, the current value of CMBR temperature is reported to be:

As per COBE/FIRAS, CMBR temperature is reported to be:.

From our recent analysis of conservation of angular momentum in flat space cosmology (pending publication), the maximum possible Planck scale angular momentum is:

(12)

where

Assuming angular momentum conservation, maximum possible current angular momentum is:

(13)

Hence, the maximum possible current angular velocity is:

(14)

Based upon this extremely small derived maximum theoretical value, our pending angular momentum paper concludes “this number is well beyond our ability to observe cosmic rotation effects in the present” or, presumably, even at the universal age at recombination.

Thus, our model predicts that rotational effects are unlikely to be detectable in higher resolutions of the cosmic microwave background radiation (CMBR).

As our cosmic model is always assumed to be expanding at light speed, from the beginning of the Planck scale, cosmic age can be expressed as follows:

(15)

For the current case, since is very small and

(16)

5. Our Model Correlations with Observed Cosmic Redshifts

We have proposed simple model equations (relations 17 - 23) for observed and predicted cosmic redshifts [2] , including the CMBR redshift. One particularly simple model equation under current study is:

(17)

and where and represent current and past cosmic radii, respectively. With reference to the assumed equivalent cosmic temperature [2] , redshift term Z can be obtained in the following way:

(18)

From relation (5) it is clear that the cosmic radius is inversely proportional to the squared cosmic temperature. The above relation (17) can be expressed, approximately, as follows:

(19)

For past higher cosmic temperatures,

(20)

This can be compared with the famous relation familiar to modern cosmologists:

(21)

Given our stated basic assumptions, our expanding cosmic model shows average mass-energy density to be inversely proportional to. See relation (11). In a very real sense, the deeper an observer from Earth looks into space (and time), the greater the temperature stage and average mass energy density stage of the cosmos one is observing. Thus, each progressively higher temperature stage and average mass density stage of the cosmos is associated with higher gravitational field strengths. So, there must be associated gravitational time dilation effects. This conclusion is firmly grounded in general relativity. Thus, it appears likely that at least a portion of the progressively higher redshift we observe with increasing look-back distance is a manifestation of gravitational time dilation. In addition, because of this inverse square relationship over very long distances, plots of proximal galactic redshifts per unit of distance observed would be expected to look relatively linear (as seen by the weaker telescopes of the 1920’s and 1930’s) and deep space galactic redshifts per unit of distance observed would be expected to clearly fall away from linearity, along with decreasing luminosity (as redshifts extend into the infrared range), similar to the 1998 Type Ia supernovae observations [5] . Such an effect may possibly create an illusion of dark energy where there is none. This is for further study.

The following graph (Figure 1), according to above relation (17), shows expected cosmic redshift as a function of the log ratio of current cosmic radius (R₀) to past cosmic radius (R_x) pertaining to a particular astronomical observation. In this manner, increasingly greater redshifts would be expected to correspond with more distant galactic observations. However, notice the apparent near-linearity below the radius ratio of about 20 (Log 1.3), and the increasingly nonlinear appearance with deeper space observations. The authors propose that something like this mathematical relationship could be useful in modeling the results of progressively deeper space observations. For data, see Table 1. The last row of Table 1 correlates cosmic radius (R_x), Log (R_x/R₀), redshift and universal age corresponding to a temperature of 3116 K.

Thus, simple model formula relations (17) and (20) closely approximate the recombination temperature of 3000 K and CMBR redshift of 1093 believed to be related to formation of the first hydrogen atoms.

Of course, since we are modeling flat space cosmology, we are also testing a slightly more complex model formula, Minkowski’s relativistic Doppler formula for flat space:

(22)

In order to keep scaling similar to Figure 1, the velocity term in the Minkowski formula can be substituted with where. The reduced relation can be expressed as:

(23)

Figure 2 shows the Minkowski relativistic Doppler redshift term as a function of decreasing log cosmic radius ratio pertaining to progressively deeper space observations. The reader should note that the CMBR redshift of 1093 correlates with the place on the horizontal axis corresponding to log value −5.777. Perhaps more importantly, however, the reader’s attention is directed to the place on the horizontal axis corresponding to the log value of −1.5. A greatly magnified portion of this region of Figure 2 would show the nonlinearity corresponding to the earliest visible galaxies, which appear to be receding at up to about 0.95 c.

Thus, a combination of gravitational time dilation (Figure 1) and flat space relativistic Doppler effect (Figure 2) may possibly provide an explanation for the nonlinearity of deep space Type Ia supernovae observations currently being attributed to “dark energy.” The reader will, of course, object that dark energy is actually causing cosmic acceleration. However, there are recent credible arguments that the 1998 Type Ia supernovae data are

not at all conclusive in this regard. Please see 2015 references [6] and [7] . In particular, a very strong case has been made by Jun-Jie Wei, et al., that the Type Ia supernovae data are a better fit for a cosmic horizon coasting along at speed of light c [7] !

This important question requires further study.

6. Summary Discussion

Given the apparent simplicity of our mathematical model, we have been pleasantly surprised by the excellent correlation between derivations from our model formulae and astronomical observations. However, upon closer inspection, the reason for this should be fairly obvious. Science progresses not by completely discarding reliable mathematical models from the past, but by refining them along with improvements in observation. Frequently, the older formulae exist as remnants within the newer refined formulae. Such will ultimately be the case when elements of general relativity and quantum mechanics come together as “quantum gravity”.

In this tradition, our mathematical model incorporates a formula (Schwarzschild) derived from general relativity, combining it with Hubble’s velocity-distance relation [8] , conservation of angular momentum (to set a limit on cosmic rotation), and incorporating all of these relationships into formulae (relations 4) which closely resemble Hawking’s black hole temperature formula [4] . Seeds in the development of these mathematical inter-relationships can be followed in references [9] -[14] . It is, therefore, not particularly unreasonable that our mathematical formulation has some relevance to our observable universe. While it may seem mysterious to some observers that quantum terms from the Planck scale, Boltzmann’s constant, and are creeping into our cosmological equations and derivations, we predict that further iterations of this process will ultimately lead us towards a more complete theory of “quantum gravity”.

Acknowledgements

The authors express their thanks to Dr. Abhas Mitra for his kind and valuable suggestions in developing this subject. One of the authors, Seshavatharam U.V.S., is indebted to professors K.V. Krishna Murthy, Chairman, Institute of Scientific Research in Vedas (I-SERVE), Hyderabad, India and Shri K.V.R.S. Murthy, former scientist IICT (CSIR), Govt. of India, Director, Research and Development, I-SERVE, for their valuable guidance and great support in developing this subject. Author Dr. E. Terry Tatum would also like to thank Dr. Rudy Schild, Harvard Center for Astrophysics, for his support and encouragement in developing this subject.

Cite this paper

Eugene TerryTatum,U. V. S.Seshavatharam,S.Lakshminarayana, (2015) Flat Space Cosmology as a Mathematical Model of Quantum Gravity or Quantum Cosmology. International Journal of Astronomy and Astrophysics,05,133-140. doi: 10.4236/ijaa.2015.53017

References