International Journal of Astronomy and Astrophysics
Vol.05 No.01(2015), Article ID:54400,9 pages
10.4236/ijaa.2015.51001
Approximate Metric for a Rotating Deformed Mass
Francisco Frutos-Alfaro1, Paulo Montero-Camacho1, Miguel Araya1, Javier Bonatti-González2
1Space Research Center and School of Physics, University of Costa Rica, San José, Costa Rica
2Nuclear Research Center and School of Physics, University of Costa Rica, San José, Costa Rica
Email: frutos@fisica.ucr.ac.cr
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 February 2015; accepted 1 March 2015; published 4 March 2015
ABSTRACT
A new Kerr-like metric with quadrupole moment is obtained by means of perturbing the Kerr spacetime. The form of this new metric is simple as the Kerr metric. By comparison with the exterior Hartle-Thorne metric, it is shown that it could be matched to an interior solution. This approximate metric may represent the spacetime of a real astrophysical object with any Kerr rotation parameter a and slightly deformed.
Keywords:
Approximate Solutions of Einstein Equations, Kerr Metric, Erez-Rosen Metric, Quadrupole

1. Introduction
In 1963, R. P. Kerr [1] proposed a metric that describes a massive rotating object. Since then, a huge amount of papers about the structure and astrophysical applications of this spacetime appeared. Now, it is widely believed that this metric does not represent the spacetime of a rotating astrophysical object. In 1967, Hernández [2] stated that reasonable perfect fluid type solutions which might serve as source of the Kerr metric may not exist. In 1971, Thorne [3] [4] added that because of the relationship between multipole moments and angular momentum, the Kerr solution cannot represent correctly the external field of any realistic stars. Moreover, the Kerr metric has difficulties when matching it to a realistic interior metric according to [5] . However, there has been a con- siderable amount of efforts trying to match the Kerr metric with a realistic interior metric that represents a physical source, see for example [6] - [12] . For a concise and comprehensive review of the different methods that have been used in order to try and obtain an interior solution for the Kerr metric, see [13] .
In [14] and [15] , the Newman-Janis algorithm was applied to look for interior solutions. Drake and Turolla [14] also propose a general method for finding interior solutions with oblate spheroidal boundary surfaces and note that the boundary surfaces reduce to a sphere in the case with no rotation, however Vaggiu in [15] argues that it is more helpful to start with the Schwarzschild interior and then proceed to the Kerr interior. Vaggiu uses an anisotropic conformally flat static interior and is led to interior Kerr solutions with oblate spheroidal boun- dary surfaces, additionally he points out that his procedure can be applied to find interior solutions matching with a general asymptotically flat vacuum stationary spacetime.
Other exact rotating solutions to the Einstein field equations (EFE) containing mass multipoles and magnetic dipole were obtained by [16] - [23] . In the first four articles, they used the Ernst formalism [24] , while in the four last ones, the solutions were obtained with the help of the Hoenselaers-Kinnersley-Xanthopoulos (HKX) trans- formations [25] . These authors obtain new metrics from a given seed metric. These formalisms allow to include other desirable characteristics (rotation, multipole moments, magnetic dipole, etc.) to a given seed metrics. Furthermore, Quevedo in [26] not only presents an exact electrovacuum solution that can be used to describe the exterior gravitational field of a rotating charged mass distribution, but also considers the matching using the derivatives of the curvature eigenvalues, this leads to matching conditions from which one can expect to obtain the minimum radius at which the matching can be made.
In Nature, it is expected that astrophysical objects are rotating and slightly deformed as is pointed out in [27] and in [28] . In addition, Andersson and Comer in [27] use a two-fluid model for a neutron star, one layer with neutrons that has a differential rotation and another layer consisting of a solid crust with constant rotation. The aim of this article is to derive an appropriate analytical tractable metric for calculations in which the quadrupole moment can be treated as a perturbation, but for arbitrary angular momentum. Moreover, this metric should be useful to tackle astrophysical problems, for instance, accretion disk in compact stellar objects [27] - [30] , re- lativistic magnetohydrodynamic jet formation [31] , astrometry [32] [33] and gravitational lensing [34] . Further- more, software related with applications of the Kerr metric can be easily modified in order to include the quad- rupole moment [35] - [37] .
This paper is organized as follows. In Section 2, we give a succinct explanation of the Kerr metric, and the weak limit of the Erez-Rosen metric is presented. In Section 3, the Lewis metric is presented, and the pertur- bation method is discussed. The application of this method leads to a new solution to the EFE with quadrupole moment and rotation. It is checked by means of the REDUCE software [38] that the resulting metric is a solu- tion of the EFE. In section 4, we compare our solution with the exterior Hartle-Thorne metric in order to assure that our metric has astrophysical meaning. Forthcoming works with this metric are discussed in Section 6.
2. The Kerr Metric and the Erez-Rosen Metric
2.1. The Kerr Metric
The Kerr metric represents the spacetime of a non-deformed massive rotating object. The Kerr metric is given by [1] [39]
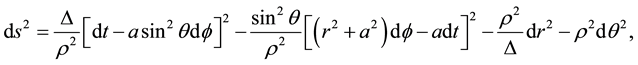 (1)
(1)
where
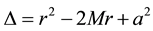 and
and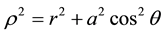 . M and a represent the mass and the rotation parameter, respectively. The angular momentum of the object is
. M and a represent the mass and the rotation parameter, respectively. The angular momentum of the object is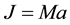 .
.
2.2. The Erez-Rosen Metric
The Erez-Rosen metric [39] - [42] represents the spacetime of a body with quadrupole moment. The principal axis of the quadrupole moment is chosen along the spin axis, so that gravitational radiation can be ignored. Here, we write down an approximate expression for this metric obtained by doing Taylor series [32]
 (2)
(2)
where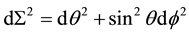 , and
, and
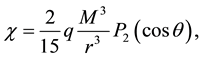 (3)
(3)
where . The quadrupole parameter is given by
. The quadrupole parameter is given by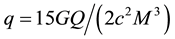 , with Q representing the quadrupole moment. This metric is valid up to the order
, with Q representing the quadrupole moment. This metric is valid up to the order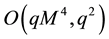 .
.
3. Perturbing the Kerr Metric
3.1. The Lewis Metrics
The Lewis metric is given by [39] [43]
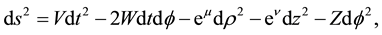 (4)
(4)
where we have chosen the canonical coordinates
 and
and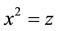 , V, W, Z, m and n are functions of r and z
, V, W, Z, m and n are functions of r and z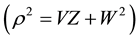 . Choosing
. Choosing
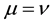 and performing the following changes of potentials
and performing the following changes of potentials
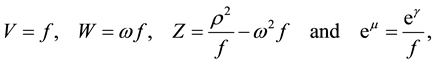
we get the Papapetrou metric

3.2. The Perturbation Method
In order to include a small quadrupole moment into the Kerr metric we will modify the Lewis-Papapetrou metric (5). First of all, we choose expressions for the canonical coordinates r and z. For the Kerr metric [1] , one particular choice is [39] [44]

where
From (6) we get

If we choose
the term (7) becomes
where
From (5), we propose the following metric

where

where the potentials




Now, let us choose

The only potential we have to find is

where

In our calculations, we consider the potential

Terms containing factors of the form
are also neglected. Substituting the known potentials



The solution for this equation is

where



Then, the new modified Kerr metric containing quadrupole moment is

where the tilde over

We verified that the metric (14) is indeed a solution of the EFE using REDUCE [38] up to the order
Note that (14) has four important limiting cases. One obtains the Kerr metric (1) if



4. Comparison with the Exterior Hartle-Thorne Metric
In order to validate the metric (14) as representing the gravitational field of a real astrophysical object, one should show that it is possible to construct an interior solution, which can appropriately be matched with our exterior solution. To this aim, we employed the exterior Hartle-Thorne metric [5] [32] [45] [46]

where


The spacetime (14) has the same weak limit as the metric obtained by Frutos-Alfaro et al. [32] . A comparison of the exterior Hartle-Thorne metric (15) with the weak limit of the metric (14) shows that upon defining

both metrics coincide up to the order
5. Conclusions
The new Kerr metric with quadrupole moment was obtained by solving the EFE approximately. It may represent the spacetime of a rotating and slightly deformed astrophysical object, which is possible since it can match an interior solution. We showed this by comparison of our metric with the exterior Hartle-Thorne metric. The limit- ing cases for the new Kerr metric correspond to the Kerr metric, the Erez-Rosen-like metric, and the Schwarz- schild metric as expected.
The inclusion of the quadrupole moment in the Kerr metric is more suitable for astrophysical calculations than the Kerr metric alone and there are a large variety of applications which can be tackled with this new metric. Amongst the applications for this metric are astrometry, gravitational lensing, relativistic magnetohydrodynamic jet formation, and accretion disks in compact stellar objects, additionally we would like to point out that pre- vious works in superfluid neutron stars can be repeated using this new metric instead of the Hartle-Thorne me- tric as an exterior solution. Furthermore, existing software with applications of the Kerr metric can be easily modified to include the quadrupole moment.
Acknowledgements
We thank H. Quevedo for reading the manuscript.
References
- Kerr, R.P. (1963) Gravitational Field of a Spinning Mass as an Example of Algebraically Special Metrics. Physical Review Letters, 11, 237-238. http://dx.doi.org/10.1103/PhysRevLett.11.237
- Hernández, W. (1967) Material Sources for the Kerr Metric. Physical Review, 159, 1070-1072. http://dx.doi.org/10.1103/PhysRev.159.1070
- Thorne, K.S. (1969) Relativistic Stars, Black Holes and Gravitational Waves. Sachs, B.K., Ed., General Relativity and Cosmology, Proceedings of the International School of Physics Enrico Fermi, Course XLVII, Academic Press, Waltham, 237-283. http://www.its.caltech.edu/kip/scripts/publications.html
- Marsh, G.E. (2014) Rigid Rotation and the Kerr Metric. http://arxiv.org/abs/1404.5297
- Boshkayev, K., Quevedo, H. and Ruffini, R. (2012) Gravitational Field of Compact Objects in General Relativity. Physical Review D, 86, Article ID: 064043. http://dx.doi.org/10.1103/PhysRevD.86.064043
- Cuchí, J.E., Molina, A. and Ruiz, E. (2011) Double Shell Stars as Source of the Kerr Metric in the CMMR Approximation. Journal of Physics: Conference Series, 314, Article ID: 012070.
- Krisch, J.P. and Glass, E.N. (2009) Counter-Rotating Kerr Manifolds Separated by a Fluid Shell. Classical and Quantum Gravity, 26, Article ID: 175010. http://dx.doi.org/10.1088/0264-9381/26/17/175010
- Haggag, S. and Marek, J. (1981) A Nearly-Perfect-Fluid Source for the Kerr metric. Il Nuovo Cimento B, 62, 273-282. http://dx.doi.org/10.1007/BF02721277
- Haggag, S. (1990) A Fluid Source for the Kerr Metric. Il Nuovo Cimento B, 105, 365-370. http://dx.doi.org/10.1007/BF02728818
- Haggag, S. (1990) A Static Axisymmetric Anisotropic Fluid Solution in General Relativity. Astrophysics and Space Science, 173, 47-51. http://dx.doi.org/10.1007/BF00642561
- Krasi?ski, A. (1980) A Newtonian Model of the Source of the Kerr Metric. Physics Letters, 80A, 238-242. http://dx.doi.org/10.1016/0375-9601(80)90010-9
- Ramadan, A. (2004) Fluid Sources for the Kerr Metric. Il Nuovo Cimento, 119B, 123-129.
- Krasi?ski, A. (1978) Ellipsoidal Space-Times, Sources for the Kerr Metric. Annals of Physics, 112, 22-40. http://dx.doi.org/10.1016/0003-4916(78)90079-9
- Drake, S.P. and Turolla, R. (1997) The Application of the Newman-Janis Algorithm in Obtaining Interior Solutions of the Kerr Metric. Classical and Quantum Gravity, 14, 1883-1897. http://dx.doi.org/10.1088/0264-9381/14/7/021
- Viaggiu, S. (2006) Interior Kerr Solutions with the Newman-Janis Algorithm Starting with Physically Reasonable Space-Times. International Journal of Modern Physics D, 15, 1441-1453. http://dx.doi.org/10.1142/S0218271806009169
- Castejon-Amenedo, J. and Manko, V.S. (1990) Superposition of the Kerr Metric with the Generalized Erez-Rosen Solution. Physical Review D, 41, 2018-2020. http://dx.doi.org/10.1103/PhysRevD.41.2018
- Manko, V.S. and Novikov, I.D. (1992) Generalizations of the Kerr and Kerr-Newman Metrics Possessing an Arbitrary Set of Mass-Multipole Moments. Classical and Quantum Gravity, 9, 2477-2487. http://dx.doi.org/10.1088/0264-9381/9/11/013
- Manko, V.S., Mielke, E.W. and Sanabria-Gómez, J.D. (2000) Exact Solution for the Exterior Field of a Rotating Neutron Star. Physical Review D, 61, Article ID: 081501. http://dx.doi.org/10.1103/PhysRevD.61.081501
- Pachón, L.A., Rueda, J.A. and Sanabria-Gómez, J.D. (2006) Realistic Exact Solution for the Exterior Field of a Rotating Neutron Star. Physical Review D, 73, Article ID: 104038. http://dx.doi.org/10.1103/PhysRevD.73.104038
- Quevedo, H. (1986) Class of Stationary Axisymmetric Solutions of Einsteins Equations in Empty Space. Physical Review D, 33, 324-327. http://dx.doi.org/10.1103/PhysRevD.33.324
- Quevedo, H. (1989) General Static Axisymmetric Solution of Einsteins Vacuum Field Equations in Prolate Spheroidal Coordinates. Physical Review D, 39, 2904-2911. http://dx.doi.org/10.1103/PhysRevD.39.2904
- Quevedo, H. and Mashhoon, B. (1991) Generalization of Kerr Spacetime. Physical Review D, 43, 3902-3906. http://dx.doi.org/10.1103/PhysRevD.43.3902
- Quevedo, H. (2011) Exterior and Interior Metrics with Quadrupole Moment. General Relativity and Gravitation, 43, 1141-1152. http://dx.doi.org/10.1007/s10714-010-0940-5
- Ernst, F.J. (1968) New Formulation of the Axially Symmetric Gravitational Field Problem. Physical Review, 167, 1175-1177. http://dx.doi.org/10.1103/PhysRev.167.1175
- Hoenselaers, C., Kinnersley, W. and Xanthopoulos, B.C. (1979) Symmetries of the Stationary Einstein-Maxwell Equations. VI. Transformations Which Generate Asymptotically Flat Spacetimes with Arbitrary Multipole Moments. Journal of Mathematical Physics, 20, 2530-2536. http://dx.doi.org/10.1063/1.523580
- Quevedo, H. (2012) Matching Conditions in Relativistic Astrophysics. In: Damour, T., Jantzen, R.T. and Ruffini, R., Eds., Proceedings of the Twelfth Marcel Grossmann Meeting on General Relativity, World Scientific, Singapore. http://arxiv.org/abs/1205.0500
- Andersson, N. and Comer, G.L. (2001) Slowly Rotating General Relativistic Superfluid Neutron Stars. Classical and Quantum Gravity, 18, 969-1002. http://dx.doi.org/10.1088/0264-9381/18/6/302
- Stergioulas, N. (2003) Rotating Stars in Relativity. Living Reviews in Relativity, 6. http://www.livingreviews.org/lrr-2003-3
- Fragile, P.C., Blaes, O.M., Anninos, P. and Salmonson, J.D. (2007) Global General Relativistic Magnetohydrodynamic Simulation of a Tilted Black Hole Accretion Disk. Astrophysical Journal, 668, 417-429. http://dx.doi.org/10.1086/521092
- Hawley, J.F. (2009) MHD Simulations of Accretion Disks and Jets: Strengths and Limitations. Astrophysics and Space Science, 320, 107-114. http://dx.doi.org/10.1007/s10509-008-9799-2
- Fendt, C. and Memola, E. (2008) Formation of Relativistic MHD Jets: Stationary State Solutions and Numerical Simulations. International Journal of Modern Physics, D17, 1677-1686. http://dx.doi.org/10.1142/S0218271808013297
- Frutos-Alfaro, F., Retana-Montenegro, E., Cordero-Garca, I. and Bonatti-González, J. (2013) Metric of a Slow Rotating Body with Quadrupole Moment from the Erez-Rosen Metric. International Journal of Astronomy and Astrophysics, 3, 431-437. http://dx.doi.org/10.4236/ijaa.2013.34051
- Soffel, M.H. (1989) Relativity in Astrometry, Celestial Mechanics and Geodesy (Astronomy and Astrophysics Library). Springer-Verlag, Berlin. http://www.springer.com/us/book/9783642734083
- Frutos-Alfaro, F. (2001) A Computer Program to Visualize Gravitational Lenses. American Journal of Physics, 69, 218-222. http://dx.doi.org/10.1119/1.1290251
- Dexter, J. and Algol, E. (2009) A Fast New Public Code for Computing Photon Orbits in a Kerr Spacetime. Astrophysical Journal, 696, 1616-1629. http://dx.doi.org/10.1088/0004-637X/696/2/1616
- Frutos-Alfaro, F., Grave, F., Müller, T. and Adis, D. (2012) Wavefronts and Light Cones for Kerr Spacetimes. Journal of Modern Physics, 3, 1882-1890. http://dx.doi.org/10.4236/jmp.2012.312237
- Vincent, F.H., Paumard, T., Gourgoulhon, E. and Perrin, G. (2011) GYOTO: A New General Relativistic Ray-Tracing Code. Classical and Quantum Gravity, 28, Article ID: 225011. http://dx.doi.org/10.1088/0264-9381/28/22/225011
- Hearn, A.C. (1999) REDUCE (User’s and Contributed Packages Manual). Konrad-Zuse-Zentrum für Informationstechnik, Berlin. http://www.reduce-algebra.com/docs/reduce.pdf
- Carmeli, M. (2001) Classical Fields: General Relativity and Gauge Theory. World Scientific Publishing, Singapore. http://www.worldscientific.com/worldscibooks/10.1142/4843
- Winicour, J., Janis, A.I. and Newman, E.T. (1968) Static, Axially Symmetric Point Horizons. Physical Review, 176, 1507-1513. http://dx.doi.org/10.1103/PhysRev.176.1507
- Young, J.H. and Coulter, C.A. (1969) Exact Metric for a Nonrotating Mass with a Quadrupole Moment. Physical Review, 184, 1313-1315. http://dx.doi.org/10.1103/PhysRev.184.1313
- Zel’dovich, Y.B. and Novikov, I.D. (2011) Stars and Relativity. Dover Publications, New York. http://store.doverpublications.com/0486694240.html
- Lewis, T. (1932) Some Special Solutions of the Equations of Axially Symmetric Gravitational Fields. Proceedings of the Royal Society of London A, 136, 176-192. http://dx.doi.org/10.1098/rspa.1932.0073
- Chandrasekhar, S. (2000) The Mathematical Theory of Black Holes. Oxford University Press, Oxford. http://www.oupcanada.com/catalog/9780198503705.html
- Hartle, J.B. and Thorne, K.S. (1968) Slowly Rotating Relativistic Stars. II. Models for Neutron Stars and Supermassive Stars. Astrophysical Journal, 153, 807-834. http://dx.doi.org/10.1086/149707
- Berti, E., White, F., Maniopoulou, A. and Bruni, M. (2005) Rotating Neutron Stars: An Invariant Comparison of Approximate and Numerical Spacetime Models. Monthly Notices of the Royal Astronomical Society, 358, 923-938. http://dx.doi.org/10.1111/j.1365-2966.2005.08812.x
- Sato, H. and Tomimatsu, A. (1973) Gravitational Field of Slowly Rotating Deformed Masses. Progress of Theoretical Physics, 49, 790-799. http://ptp.oxfordjournals.org/content/49/3/790.full.pdf
- Hernández-Pastora, J.L. (2006) Approximate Gravitational Field of a Rotating Deformed Mass. General Relativity and Gravitation, 38, 871-884. http://dx.doi.org/10.1007/s10714-006-0269-2
Appendix
The non-null Ricci tensor components for the metric (8) are given by (with the tilde over

Calculation of the scalar curvature (with the tilde over
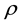 dropped)
dropped)












