International Journal of Astronomy and Astrophysics
Vol.1 No.4(2011), Article ID:16373,4 pages DOI:10.4236/ijaa.2011.14022
Similarity of Rayleigh-Taylor Instability Development on Scales from 1 mm to One Light Year
1School of Electrical and Computer Engineering, Cornell University, Ithaca, USA
2Department of Atmospheric, Oceanic and Space Science, University of Michigan, Ann Arbor, USA
3Geophysical Institute, University of Alaska, Fairbanks, USA
E-mail: mck13@cornell.edu
Received July 15, 2011; revised September 18, 2011; accepted October 9, 2011
Keywords: Rayleigh-Taylor Instability, Decelerating Fluid, Exploding Star, Active Experiment
Abstract
In this paper, we describe three different phenomena occurring on scales of 1 mm, 100 km, and almost a light year. The smallest scale is a laboratory experiment. The intermediate scale is a rocket-borne space experiment and the largest is an exploding star. In each case, deceleration creates a situation that is unstable to the Rayleigh-Taylor instability. The similarity exists in the spatial and in the Fourier domains; that is, not only are there obvious spatial similarities but the power spectra of the two phenomena are also nearly identical. The data compare favorably to published simulations.
1. Introduction
As shown in the right-hand side of Figure 1, supernova SN1987A was photographed using one of the Hubble cameras [1]. The elliptical region of interest, the He/H interface in the supernova (SN), is accelerated by a blast wave that is created after the core of the star explodes. The long-axis diameter of the structure was 1.2 ´ 1013 km. The event has been studied in detail, and the hydrodynamic Rayleigh-Taylor instability is clearly the origin of the clumping seen in the photo [2,3]. Here we compare this natural event to two experiments involving the Rayleigh-Taylor instability. Our main point is that the evolution of this nonlinear process is nearly identical over 19 orders of magnitude in scale.
The sounding rocket experiment was launched from the
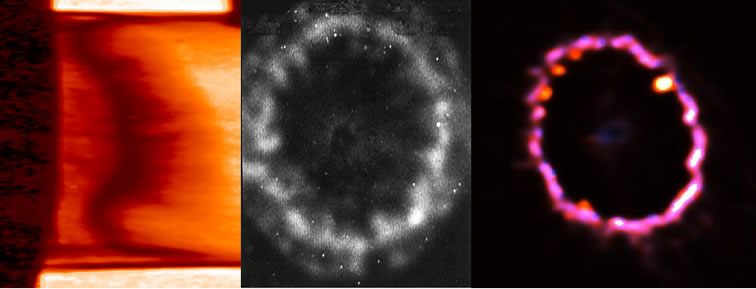
Figure 1. From left to right, a laboratory experiment, a rocket-borne space experiment, and a Hubble photo of the SN1987A supernova.
Poker Flat Research Range north of Fairbanks, Alaska [4]. A radial-shaped charge was lined with barium, which is vaporized using the thermite reaction, accelerated by the shaped charge explosion, and carried away at several km/s. Sunlight at apogee allows the gas to be seen on the ground. The photo was taken from Ft. Yukon nearly exactly up the magnetic field lines. As the vapor expands, it collides with the neutral gas, decelerating and creating an artificial gravity, an inertial force pointed back toward the rocket. The resulting structure is Rayleigh-Taylor unstable, creating the observed structures in the middle panel of Figure 1. The diameter of the ring is 50 km.
The hydrodynamic processes that occur in a core-collapse supernova, such as SN1987A, and in the rocket experiment described earlier can be simulated in a wellscaled experiment using a high-powered laser [5-7]. Kuranz et al. [8] used this method to study the hydrodynamic instabilities that occur at the interface between the helium and hydrogen layers during the blast-wave-driven explosion phase of the supernova (SN). It is possible to experimentally study such supernova-relevant hydrodynamics because both the experiment and the related part of the SN satisfy similarity conditions based on the Euler equations [5]. The Euler equations remain invariant under a transformation relating the two systems. Also, in all three systems studied here, several similarity criteria are satisfied, including all three systems being highly collisional and having negligible heat conduction, radiation flux, viscosity, and gravitational and magnetic effects. Having satisfied the pertinent scaling conditions, the two experiments will have a similar hydrodynamic evolution.
Another important similarity factor is the acceleration/deceleration of the systems. In the laboratory experiment, a blast-wave structure crosses a density drop. This is accomplished using laser beams at the Omega laser [1] facility to create a shock wave in the denser material by producing an ablation pressure of ~50 Mbars. The laser pulse ends when the shock is approximately halfway through this material. The plasma that has been created expands, causing a rarefaction wave in the material that overtakes the shock. This creates a blast-wave structure moving towards an interface with a density drop. This scenario includes a pressure gradient, created by the blast wave, in the opposite direction of a density gradient, created by the drop in density at the interface. This causes the Rayleigh-Taylor instability [9,10] to develop.
The experiment uses a millimeter-scale target that consists of a drop in density scaled to SN1987A. The denser material is composed mostly of 150 µm thick polyimide (C22H10O5N2) with a density of 1.41 g/cm3. It is followed by a few mm of carbonized resorcinol formaldehyde (CRF) foam, which has a density of 50 mg/cm3. The primary diagnostic in this experiment is x-ray radiography. A separate target is used to create ~4 keV x-rays for the purpose of imaging the experiment. Experimental radiographs can be seen in the left-hand panel of Figure 1. In each image, the shock waves are moving to the right with the interface behind it. The structure on the interface is due to the Rayleigh-Taylor instability.
In the remainder of the text, we concentrate on comparing the rocket and Hubble data, since they are both cylindrically symmetric in two dimensions.
2. Analysis
The supernova and rocket photos can be most easily compared. The light intensities of both structures were determined as functions of angular distance. Rotating the image from the sounding rocket experiment from Yukon, Alaska 38˚ counter-clockwise reveals the similarities to that of the Hubble image of the SN1987A, as shown in Figure 2. Both display about 15 blobs spaced 30˚ or so apart, as shown Figure 2 and in the spectra shown in Figure 3.
The self-similarity of these spectral features is remarkable. There are sharp peaks around 2 rad–1 followed by power law, where the power law index for the rocketborne experiment and SN1987A are about 3.9 and 4.8, respectively.
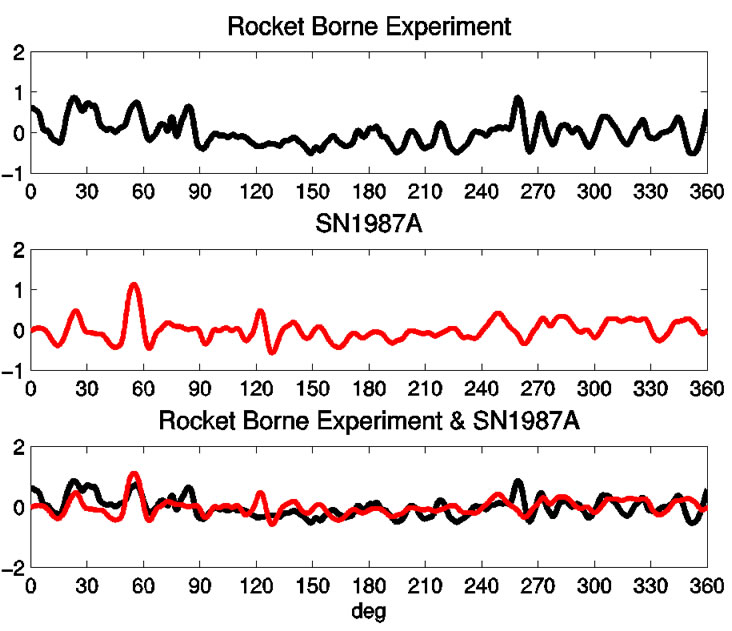
Figure 2. The angular intensities of an image from the rocket-borne space experiment at Yukon, Alaska compared to that of a Hubble image of SN1987A.
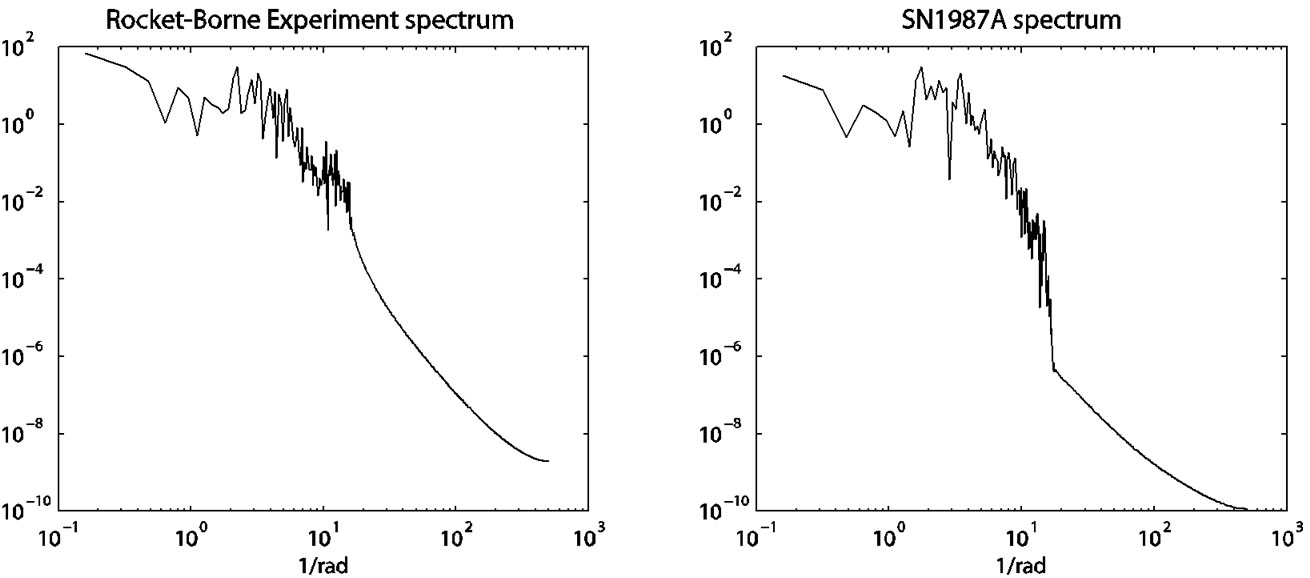
Figure 3. The spectrum of the ring features of the rocket-borne space experiment at Yukon, Alaska compared to that of a Hubble image of SN1987A.
Numerical simulations have been reported [2,3] and the clumping verified. In Figure 4, we compare the simulation with both experiments and, in Figure 5, plot the spectrum of the simulation. Note that like the spectra of rocket-borne space experiment and the Hubble image of SN1987A, there is also a peak at 2 rad-1 followed by a power law of similar magnitude. The power law indicates a shock-like development.
The linear growth rate for the Rayleigh-Taylor instability is,
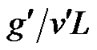 (1)
(1)
where g¢ is the effective gravity, v', is the effective collision frequency, and L is the gradient scale length. This

Figure 4. A comparison of azimuthal structures from the rocket-borne space experiment at Yukon, Alaska, a Hubble image of SN1987A, and numerical simulations done by Fryxell et al. [2].

Figure 5. The spectrum of the ring features of numerical simulations by Fryxell et al. [2].
has been shown to apply to the Hubble event [5] and here we check it against the rocket experiment. The expanding barium cools, leading to a thermal velocity of around 200 m/s. This wind drives a current given by J = s(U × B), which drives the instability. From the photographs, L ~ 2000 m, leading to a growth rate of 3 Hz. In the 40-second development, many e-folds are possible and the nonlinear approach is suitable.
3. Conclusions
These data and analyses show a self-similarity of the Rayleigh-Taylor instability over 19 orders of magnitude in scale.
4. Acknowledgements
This work was supported by the National Science Foundation (grant ATM-0551107) at Cornell University. Support for the original experiments was provided though NASA grants to the University of Alaska Fairbanks. Work at the University of Michigan is supported by the U.S. DOE National Nuclear Security Administration under the Stewardship Sciences Academic Alliances program (grant DE-FG52-04NA00064) and the National Laser User Facility (DE-FG03-00SF22021)
5. References
[1] “Gas Ring around Super Nova 1987A,” online image, 2 February 2000, cited July 2008. http://hubblesite.org/gallery/album/entire_collection/pr2000011b/
[2] B. Fryxell, E. Muller and D. Arnett, “Instabilities and Clumping in SN 1987A. I—Early Evolution in Two Dimensions,” The Astrophysical Journal, Vol. 367, 1991, pp. 619-634. doi:10.1086/169657
[3] E. Muller, B. Fryxell and D. Arnett, “Instability and Clumping in SN 1987A,” The Astrophysical Journal, Vol. 251, 1991, pp. 505-514.
[4] E. M. Wescott, H. C. Stenbaek-Nielsen, T. Hallinan, C. Deehr, J. Romich, J. Olson, M. C. Kelley, R. Pfaff, R. B. Torbert, P. Newell, H. Foppl, J. Fedder and H. Mitchell, “Plasma-Depleted Holes, Waves, and Energized Particles from High-Altitude Explosive Plasma Perturbation Experiments,” Journal of Geophysical Research, Vol. 90, No. A5, 1985, pp. 4281-4298. doi:10.1029/JA090iA05p04281
[5] D. D. Ryutov, R. P. Drake, J. Kane, E. Liang, B. A. Remington and M. Wood-Vasey, “Similarity Criteria for the Laboratory Simulation of Supernova Hydrodynamics,” The Astrophysical Journal, Vol. 518, No. 2, 1999, pp. 821-832. doi:10.1086/307293
[6] J. Kane, D. Arnett, B. A. Remington, S. G. Glendinning, G. Bazan, R. P. Drake, B. A. Fryxell, R. Teyssier and K. Moore, “Scaling Supernova Hydrodynamics to the Laboratory,” Physics of Plasmas, Vol. 6, No. 5, 1999, pp. 2065- 2072. doi:10.1063/1.873497
[7] R. P. Drake, “Laboratory Experiments to Simulate the Hydrodynamics of Supernova Remnants and Supernovae,” Journal of Geophysical Research, Vol. 104, No. A7, 1999, pp. 14505-14515. doi:10.1029/98JA02829
[8] C. C. Kuranz, R. P. Drake, D. R. Leibrandt, E. C. Harding, H. F. Robey, A. R. Miles, B. E. Blue, J. F. Hansen, H. Louis, M. Bono, J. Knauer, D. Arnett and C. A. Meakin, “Progress toward the Study of Laboratory Scale, Astrophysically Relevant, Turbulent Plasmas,” Astrophysics and Space Science, Vol. 298, No. 1-2, 2005, pp. 9-16. doi:10.1007/s10509-005-3906-4
[9] L. Rayleigh, “Scientific Papers,” Vol. II, Cambridge University Press, Cambridge, 1900.
[10] G. I. Taylor, “The Instability of Liquid Surfaces When Accelerated in a Direction Perpendicular to Their Planes,” Proceedings of the Royal Society of London, Vol. A201, No. 1065, 1950, pp. 192-196.

