Received 16 November 2015; accepted 4 December 2015; published 7 December 2015

ABSTRACT

Linear algebra provides insights into the description of elasticity without stress or strain. Classical descriptions of elasticity usually begin with defining stress and strain and the constitutive equations of the material that relate these to each other. Elasticity without stress or strain begins with the positions of the points and the energy of deformation. The energy of deformation as a function of the positions of the points within the material provides the material properties for the model. A discrete or continuous model of the deformation can be constructed by minimizing the total energy of deformation. As presented, this approach is limited to hyper-elastic materials, but is appropriate for infinitesimal and finite deformations, isotropic and anisotropic materials, as well as quasi-static and dynamic responses.

Keywords:

Elasticity, Stress, Strain, Finite Elasticity

1. Introduction

Soft materials like rubber, foam, and many biological materials can stretch far beyond the limits of infinitesimal elasticity and yet return to their original shape when forces are removed. It is useful to be able to model these deformations, but infinitesimal elasticity based on stress and strain tensors cannot be used for these large deformations. The classical equations of finite elasticity are quite difficult, requiring 30 or more tensors to explain the theory. The description of elasticity presented here presents the same equations for both infinitesimal and finite elasticity, and requires only two tensors to define the theory.

The description of elasticity presented here will be for hyper-elastic materials. A hyper-elastic material stores energy when it is deformed and returns this energy to its surroundings when it is returned to its original state. Rubber is the most common example. The energy stored in the material can be expressed as a function of the positions of the points within the material. By minimizing the stored energy, differential equations of elasticity and forces can be found. The idea of describing deformations in terms of points and forces was first used by Euler, Lagrange, and Poisson and predates Cauchy’s introduction of stress and strain [1] . The earlier researchers, however, did not complete the description of the general differential equations for finite elasticity. I will do that here. To do this, I will follow the notation of Spencer [2] to describe the positions of the points within the body before and after deformation.

2. Deformation as a Mapping

Define the initial location of each point within a material as the vector, 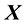, with components,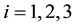. After the deformation, each point in the material will be at some new position, 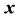, with components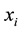,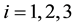. The components of each point after the deformation are functions of the components of the position of each point before deformation. That is

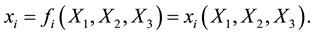(1)

To match the physical reality of the deformation of a material, neither inversions nor a change of dimension of the material will be allowed (i.e. a three-dimensional material cannot be turned inside out or pressed into a plane or a line). As a result of this restriction, every point in the material after the deformation will correspond to exactly one point in the material before deformation, so that the mapping from 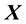to 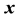is one-to-one.

Consider now a point near the point, i.e.. The point 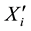is mapped into the point. We can find the relationship between 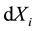and 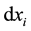by differentiating Equation (1) and using the chain rule to give

(2)

here and throughout the rest of this paper, the Einstein summation notation is used so that repeated indices are summed over. In general will vary from point to point within the material (see Figure 1). The 3 × 3 matrix formed by these values,

(3)

is called the deformation gradient tensor by Spencer [2] . The results found so far are appropriate for any coordinate system, but I will use two specific inertial coordinate systems (i.e. fixed coordinate systems where New-

ton’s laws apply). One I will call the observer coordinate system. This coordinate system is the one chosen to solve some problem in (e.g. a simulation or an engineering problem). The second inertial coordinate system I will call the experimental coordinate system. This coordinate system will be the one chosen by an experimentalist who wishes to measure the energy associate with a particular deformation of a particular sample. In the observer coordinate system, I will denote the components of as. In the experimental coordinate system I will denote the components as. I will first describe how the experimenter should measure the material properties of the material in his coordinate system.

3. Measuring the Energy of Deformation

It is sufficient to limit experimental deformations to homogeneous deformations of a homogeneous portion of the material in order to define the energy of deformation. If the body is anisotropic, it is necessary to define the orientation of this anisotropy. This could be determined by a visual inspection (e.g. wood grain) or by a knowledge of how the material was made (e.g. rebar in concrete). Orient the anisotropy to align with the experimental coordinate system so that in the experimental coordinate system the anisotropic coordinate system of the materi-

al is for, and, or. (Note that here the super-

script, k, denotes which coordinate vector and the subscript, i, denotes which component.) Using the notation of Equation (3), Equation (2) in the experimental coordinates system becomes

(4)

A homogeneous deformation is a deformation in which every point in the body undergoes an affine transformation. Linear algebra defines an affine transformation as a mapping that transforms any point in space to another point in space by a matrix transformation, followed by a translation. Applying this to our material body, every point in the body after the deformation, , corresponds to a point before the deformation, , as

(5)

where

= coordinates of the position of any point before the deformation,

= coordinates of the position of this same point after the deformation,

= 3 × 3 matrix of values that are the same throughout the body, and

= components of a vector that are the same throughout the body.

Taking the derivative of Equation (5) and comparing the result with Equation (4), we find that in our experimental coordinate system. Equation (5) indicates that to completely define any deformation in our experimental coordinate system, we need the nine components of and the three components. These 12 values can be found by recording the location of any four non-coplanar points in the experimental material before and after the homogeneous deformation. The coordinates of each of these points provides and in Equation (5). Since there are four points with three components each, this gives a total of 12 equations and 12 unknowns of the form of Equation (5). From these 12 equations, all 12 components of and can be found for any experimental deformation.

To measure the energy during experiments, record the applied forces, , and the corresponding displacements of the points where these forces are applied, with m = 1 to M, where M is the number of applied forces. The energy of deformation is the total work done by these forces, i.e. the sum of the integrals from the initial to the final position of the points where the forces are applied:

(6)

The energy per original volume, E, is found by dividing the total energy by the initial volume of the sample, V.

(7)

With these measurements, an experimenter can construct a table of the stored energy per unit initial volume as a function of the 12 components of and. To complete the description, use a linear interpolation or an equation fit to the table of data to define E as a continuous function of and, i.e.

(8)

This completely defines the energy per unit original volume for homogeneous deformations of the material sample.

4. Special Experimental Cases

We have found that in general the experimentally measured energy per unit volume, E, can be a function of as many as 12 component values (nine in and three in). It is a bit much to expect an experimenter to map out a 12 dimensional energy space for every material for every application, so it is useful to find some simplifications depending upon the particular material and application we are interested in. For example, for most applications, the only external body force that needs to be considered is gravity. In that case, we only need to express the energy of translation as a function of, where corresponds to the direction of the gravitational force and the displacement of the center of mass of the material. If the experimental coordinate system is aligned so that the third component of is parallel with the gravitational force, we only need to include energy changes due to and can omit the two variables and in our energy function, because these displacements will result in no change in the energy of the body.

A further reduction of parameters for rotations and deformations can be found if we take a Singular Value Decomposition (SVD) of. The SVD of a matrix uniquely divides the matrix into three matrices, two rotational (and), and one diagonal,. In particular,

(9)

This form will be useful in describing both experimental processes to measure the energy of deformation and the equations of elasticity. Since any deformation, , can be expressed uniquely as, then every possible deformation can be considered a combination of a rotation, followed by a stretch or compression along the three fixed orthogonal coordinate axes, , followed by a final rotation,.

In the most general case the energy of the material can depend upon body forces from electric or magnetic forces in addition to gravity. For example, a material with an electric dipole () or a magnetic dipole () in an electric () or magnetic () field, will have energy or, respectively so that the energy will be a function of, , and. If the material has a charge, q, energy must include. In these cases the energy of deformation may be a function of all nine variables in as well as the three variables in. If the electric and magnetic body forces are not significant in a particular application, the three components of need not be included in calculating E since in that case the energy associated with deformations are independent of body rotations after the deformation.

If the body is isotropic, then the energy will be independent of both and since rotating the body before or after the deformation will produce no change in the energy of deformation. In that case only the three diagonal values of, , are needed to describe the energy associated with deformation. If in addition, the material can be considered incompressible, then the volume of the material, V, is constant

(10)

and only two independent elements of need to be used to describe the energy during a deformation.

In addition to these simplifications, it is sufficient to measure the energy as a function of only those changes that are expected in a particular application. So for example, if infinitesimal deformations are sufficient to model the problem at hand, only one small displacement measurement in each direction is required. Alternatively, if the body is going to be used only in extension, there is no need to measure the energy associated with compressional forces. Rivlin [3] used this approach for rubber. For his application the rubber could be considered isotropic and incompressible, so he only deformed the material sample in extension along two perpendicular directions. This is sufficient to find the energy as a function of and.

Finally, if a deformation contains only rigid body motions, materials are neither compressed nor extend, so that for. Thus a rigid body rotation, Equation (9) gives. Since rigid body rotations can be expressed in terms of a single rotation matrix, the six parameters in and reduce to only three.

What we have found is that we can reduce the number of variables that the energy is a function of from 12 to as few as 2 in the case of an incompressible, isotropic material where we can ignore external body forces like gravity in our application. In general, however, all 12 variables may be required and it is helpful to find the most computationally efficient way to represent the energy for each application.

5. Some Application Issues

We have found that can be used to simplify the experimental measurements for particular cases; however, SVD is a rather computationally heavy calculation to be used during simulations. It is therefore useful to represent the deformations in a more computationally efficient manner for applications. For example, if we consider the case where the material is isotropic and there are no body forces, the energy per unit volume is a function of only. Thus any three independent variables spanning the same space as may be used to characterize the energy function. The values, , and can be rewritten [4] as

(11)

In addition

(12)

where, , and are the column vectors of. Thus in simulations of isotropic bodies it is not necessary to compute SVD as the simulation progresses. All that is required are the components of to compute the needed three independent values. As a result it is best in this case to redefine the experimentally defined energy,

as after the experiments are completed. Once E has been converted from a function of to a function of the column vectors of, it is only necessary to find the components of during simulations. The is no longer required.

If the material is anisotropic, the energy per unit volume is a function of the six independent values of and, Three from the diagonal elements of and three angles from. QR decomposition, , provides a more efficient venue for calculations than does. (For this application we must use the Gram-

Schmidt QRD algorithm instead of the more common Householder QRD, because the Householder algorithm permits inversions.) produces, where is an upper triangular matrix and R is a rotation matrix. Since the energy of deformation is independent of any rotation after the deformation, the six components of, like the three values of for the isotropic case, can be used to define the energy of deformation. The Gram-Schmidt QRD algorithm is not a particularly heavy numerical calculation and can be used in applications, but an alternative is also possible. As I have noted previously [5] the components of can be written in terms of dot and cross products of the column vectors of. Thus the energy of deformation can be written in terms of dot and cross products of the column vectors of and once the energy is expressed in these terms, it is not necessary to calculate any other tensors than in carrying out applications; however, we do have to consider the orientation of any anisotropy for engineering applications.

6. Coordinate Alignment

When an anisotropic material is placed in “service” it is necessary to know the initial orientation of the anisotropy. This is because the stored energy is a function of the orientation of the isotropic material relative to the observer’s coordinate system. For example consider a laminate. If the laminate is oriented so that the lamina are parallel to the x-y plane in the observer’s coordinate system and extended in the x direction a fixed amount there will be a change in energy of the material. However, if the same laminate is initially oriented so that the lamina are parallel to the y-z plane in the observer’s coordinate system and extended in the x direction the same fixed amount there will be a different change in energy of the material. Thus the initial orientation of the lamina in the observer’s coordinate system must be known in order to correctly calculate the stored energy in the material.

When the material is placed in “service” before any deformation has occurred, the anisotropic coordinate system in which the energy measurements were made, , and the observer coordinate system, , may not align. Define a rotation matrix, , where maps the components of the observer’s coordinate system, , into the components of anisotropic coordinate system before any deformation, i.e.

(13)

The local deformation which is expressed in the observer’s coordinate system, , can be expressed in the experimental coordinate system, , by a simple change of coordinates of [6] ,

(14)

Note that is at most only a function of. It is not a function of since it is defined before any deformation has taken place. For an inhomogeneous material, the matrix may vary from point to point, so that the energy would be a function of as well as. (Of course any inhomogeneous material might also be made up of different materials which have different energy maps at different locations in space,.) Thus in the most general case,

(15)

So that in general,

(16)

7. Is This Energy a Scalar?

It may seem strange that we must transfer the coordinate values of the material in the observer’s coordinate system back into the experimental coordinate system in order to find the local change in energy, but this is exactly as it should be. Energy must be a scalar, which is independent of the choice of the coordinate system. That this is the case can be seen if we express the energy in terms dot products of vectors, which are independent of the coordinate choice. Note that the local anisotropy coordinate system vectors, , are mapped into a new set of vectors, , which are in general neither orthogonal, nor unit vectors (e.g. see Figure 1). In the observer’s coordinate system this mapping is

(17)

The corresponding mapping of these same vectors in the experimental coordinate system is

(18)

We can choose to express the energy as a function of the invariant, , which must have the same value in both coordinate systems. To see the connection between the maps in the different coordinate systems, expand the dot product in both systems and compare the result. In the experimental coordinate system,

(19)

In the observer’s coordinate system, where and, we have

(20)

Comparing Equation (19) to Equation (20) returns us to Equation (14) since is invariant and must be the same value in both coordinate systems.

This is the same type of explanation that must be used in expressing the energy in terms of the components of displacement vectors, although we usually do not discuss it in these terms. Usually the energy associated with the displacement can be calculated from a formula instead of having to carry out individual experiments for each material. For example, a displacement in the presence of gravity changes the energy stored in the material, but it is easily expressed as where m is the mass and is the acceleration due to gravity and no experiments are necessary. However, if we did carry out the experiments, we would measure the energy of deformation in terms of the components of in the experimental coordinate system. In that case we would need to take into account any change in the components of in the observers coordinates. For example, assume the energy stored due to gravity is expressed in the experimental coordinate system as, where the force of gravity in the experimental coordinate system has been chosen to align with. If we placed this material into an observer coordinate system where gravity is in the direction, we must first rotate the coordinate system to align the direction with the direction before “looking up” the corresponding energy that we stored in our energy map we compiled by measuring the energy in the experimental coordinate system. Of course if we choose to express the energy in terms of the dot product, all of this would take care of itself.

A word of caution is necessary here. The vectors and are the same vectors in both the observer and the experimental coordinate systems. On the other hand, the column vectors, , , and, are only de-

fined in the experimental coordinate system, and therefore the transformation in Equation (14) must be carried out before extracting the column vectors of to calculate the energy of deformation for an anisotropic body. This is not necessary for isotropic materials because in that case the energy is independent of all rotations and applying the transformation Equation (14) has no effect on the final energy calculation, i.e. the’s are the same for and.

8. Simulations

I have now completely defined a method to measure the energy of deformation of a homogeneous body experimentally and how to place the material in a given application. Because engineering applications are often complex, it is usually necessary to put this information into a computer simulation. The simplest approach is to just “pasting” small pieces of the material together to define the complete material. This can be done by randomly positioning points in the material and use these to divide the material to be simulated into small tetrahedrons of volume, each bounded by four points. The initial and final locations of these four points put into Equation (5) can be used to define the 12 parameters needed to calculate the energy per unit original volume for each tetrahedron. The total energy of the system is just the weighted sum of the energy per unit volume of each tetrahedron,

(21)

where k is summed over all the tetrahedra in the material. Apply the boundary conditions and move the internal points to produce minimum total energy, , and we have a solution. I have called this this discrete region model [4] .

An alternative method is to use a continuous Euler-Lagrange technique to minimize the functional,

(22)

The result of this approach is a set of partial differential equations which can be solved by any numerical technique (e.g. finite difference, finite element, Rayleigh-Ritz, etc.). I have called this Euler-Lagrange elasticity [5] .

9. Differential Equations

The discrete region method collapses into Euler-Lagrange elasticity if the size of each tetrahedron approaches zero as the number of tetrahedra, N, increase without bound, i.e.

(23)

To find the differential equations of elasticity we need to minimize (or find the extrema) of, i.e.

(24)

With. This is a classic Calculus of Variations problem with multiple variables [7] . The results of this minimization are the following three Euler equations:

(25)

These three equations are quite general, being appropriate for both infinitesimal and finite deformations, for isotropic and anisotropic materials, and can include surface forces, gravity, and electrical and magnetic forces.

10. Special Application Cases

If the material is homogeneous, will not be a function of. If gravity is the only external body force, E can be separated into the energy of deformation, , and energy of body forces,:

(26)

If only infinitesimal deformations are needed, then E can be expanded in a Taylor’s expansion which yields the same differential equations Landau derived for infinitesimal deformations [8] using classical stress and strain techniques.

If time dependence is required, define the Lagrangian,

(27)

where, with the mass per original volume. Finding the extrema of

(28)

results again in three Euler equations, now of the following form:

(29)

These three equations are the time dependent differential equations for hyper-elasticity [9] . All that is needed now is to include boundary conditions and force.

Boundary conditions consist of Neumann and Dirichlet boundary conditions. Dirichlet boundary conditions just set the positions of boundary points of the material. Neumann boundary conditions can be expressed in terms of applied forces on the surfaces of the material [5] ,

(30)

where are the components of the original surface area where the forces are applied. Equations (30) provide differential equations to set the boundary conditions if the applied surface forces are known.

11. Comparison to Other Elasticity Theories

The most obvious difference of this approach and classical elasticity is that in this approach there is no definition of stress or strain. Here displacements and forces are the alternatives to stress and strain. This approach also requires the definition of only one second order tensor, the deformation gradient tensor. In elasticity with stress and strain more than 30 tensors have been used to describe finite elasticity [10] [11] .

For classical elasticity with stress and strain, the invariants, or, are used to describe strain in terms of or. In that case strain is second order in the displacements, In the approach pre-

sented in this paper, the invariants used are, and the energy of deformation is calculated from the matrix itself, which is only first order in. Infinitesimal elasticity also requires compatibility equations relating stress and strain which expresses material properties as fourth order tensors. The approach given here expresses material properties for all hyper-elastic materials as a scalar, the energy per original volume, E.

Some descriptions of elasticity define and to be represented in different coordinate bases [12] . In these descriptions, is then called a two-point tensor. In this presentation, all vectors and tensors are expressed in the same coordinate bases, either all in the observer or all in the experiment coordinate systems. There are no two-point tensors.

In some descriptions of elasticity, only “objective tensors” are used to formulate the constitutive equations. Objective tensors are required to be independent of the motion of the material that is being deformed. That is, these tensors should be the same in both a fixed reference coordinate system and in a coordinate system that deforms with the material [11] . In this paper all physical quantities are expressed only in terms of one of two coordinate systems fixed in space before any deformation takes place. In this paper, neither the observer coordinates nor the experimental coordinates deform as the material deforms. Both are inertial coordinate systems fixed in space. (The anisotropy coordinates do deform in space into after a deformation, but these are not used as bases to describe the components of vectors or tensors.)

Some details may be easily confused between this approach and the Classical approach. Three examples follow:

Ÿ are not the of invariants of the right Cauchy-Green deformation tensor, which is described as. Instead the values are the diagonal elements of.

Ÿ QRD is not the same as Polar decomposition that is used in classical elasticity theory. Polar decomposition produces, where is a symmetric matrix, whereas QRD produces, where is an upper triangular matrix.

Ÿ The term in Equation (30) is equivalent to Cauchy stress only for infinitesimal deformations.

12. Conclusion

A method of describing hyper-elasticity using linear algebra has been presented that uses points within the material and forces instead of stress and strain. The theory provides a straight forward way to measure material properties and allows the inclusion of magnetic and electric fields as well as gravity. This description uses the same equations for both finite and infinitesimal deformations. Neumann boundary conditions are expressed in terms of measured forces instead of computed stresses. The result is a complete theory of hyper-elasticity which includes infinitesimal and finite deformations, isotropic and anisotropic materials, quasi-static and dynamic elastic responses.

Acknowledgements

I would like to acknowledge Mr. Joshua Wood and Dr. Michael Berglund for their very fruitful discussions and helpful suggestions.

Cite this paper

H. H.Hardy, (2015) Linear Algebra Provides a Basis for Elasticity without Stress or Strain. Soft,04,25-34. doi: 10.4236/soft.2015.43003

References