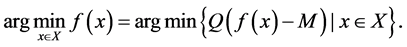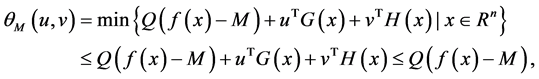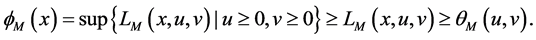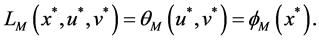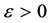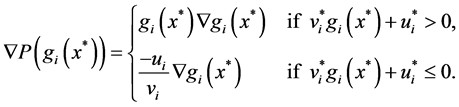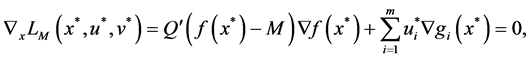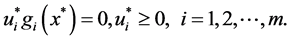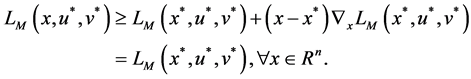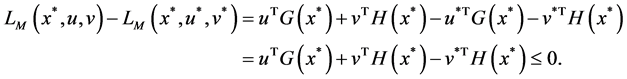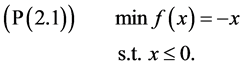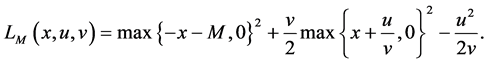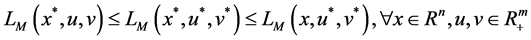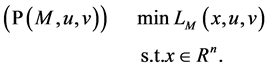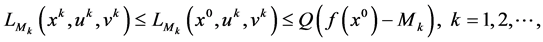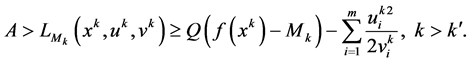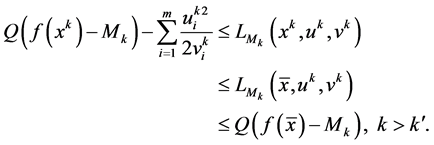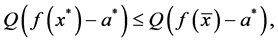Open Journal of Optimization
Vol.06 No.02(2017), Article ID:76262,8 pages
10.4236/ojop.2017.62004
A New Augmented Lagrangian Objective Penalty Function for Constrained Optimization Problems
Ying Zheng1, Zhiqing Meng2
1Department of Basic Courses, College of Basic Science, Ningbo Dahongying University, Ningbo, China
2College of Economics and Management, Zhejiang University of Technology, Hangzhou, China

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: March 25, 2017; Accepted: May 16, 2017; Published: May 19, 2017
ABSTRACT
In this paper, a new augmented Lagrangian penalty function for constrained optimization problems is studied. The dual properties of the augmented Lagrangian objective penalty function for constrained optimization problems are proved. Under some conditions, the saddle point of the augmented Lagrangian objective penalty function satisfies the first-order Karush-Kuhn-Tucker (KKT) condition. Especially, when the KKT condition holds for convex programming its saddle point exists. Based on the augmented Lagrangian objective penalty function, an algorithm is developed for finding a global solution to an inequality constrained optimization problem and its global convergence is also proved under some conditions.
Keywords:
Constrained Optimization Problems, Augmented Lagrangian, Objective Penalty Function, Saddle Point, Algorithm

1. Introduction
Augmented Lagrangian penalty functions are effective approaches to inequality constrained optimization. Their main idea is to transform a constrained optimization problem into a sequence of unconstrained optimization problems that are easier to solve. Theories on and algorithms of Lagrangian penalty function were introduced in Du’s et al. works [1] . Many researchers have tried to find alternative augmented Lagrangian functions. Many literatures on augmented Lagrangian (penalty) functions have been published from both theoretical and practical aspects (see [2] - [8] ), whose key concerns cover zero gap of dual, existence of saddle point, exactness, algorithm and so on.
All augmented Lagrangian functions consist of two parts, a Lagrangian function with a Lagrangian parameter and a penalty function with a penalty parameter (see [2] - [8] ). Dual and saddle point is the key concerns of augmented Lagrangian function. Moreover, zero gap of Lagrangian function’s dual is true only for convex programming and augmented Lagrangian function. Therefore, augmented Lagrangian function algorithms solve a sequence of constrained optimization problems by taking differential Lagrangian parameters and penalty parameters in [2] [3] [4] [5] . Lucidi [6] and Di Pillo et al. [7] obtained some results of exact augmented Lagrangian function, but numerical results were not given. R. S. Burachik and C. Y. Kaya gave an augmented Lagrangian scheme for a general optimization problem, and established for this update primal-dual convergence the augmented penalty method in [8] . However, when it comes to computation, to apply these methods, lots of Lagrangian parameters or penalty parameters need to be adjusted to solve some unconstrained optimization dual problems, which make it difficult to obtain an optimization solution to the original problem. Hence, it is meaningful to study a novel augmented Lagrangian function method.
In recent years, the penalty function method with an objective penalty parameter has been discussed in [9] - [16] . Burke [12] considered a more general type. Fiacco and McCormick [13] gave a general introduction to sequential unconstrained minimization techniques. Mauricio and Maculan [14] discussed a Boolean penalty method for zero-one nonlinear programming. Meng et al. [15] studied a general objective penalty function method. Furthermore, Meng et al. studied properties of dual and saddle points of the augmented Lagrangian objective penalty function in [16] . Here, a new augmented Lagrangian objective penalty function which differs from the one in [16] is studied. Some important results similar to those of the augmented Lagrangian objective penalty function in [16] are obtained.
The main conclusions of this paper include that the optimal target value of the dual problem and the optimal target value of the original problem is zero gap, and saddle point is equivalent to the KKT condition of the original problem under the convexity conditions. A global algorithm and its convergence are presented. The remainder of this paper is organized as follows. In Section 2, an augmented Lagrangian objective penalty function is defined, its dual properties are proved, and an algorithm to find a global solution to the original problem (P) with convergence is presented. In Section 3, conclusions are given.
2. Augmented Lagrangian Objective Penalty Function
In this paper the following mathematical programming of inequality constrained optimization problem is considered:

where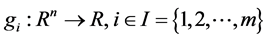 . The feasible set of (P) is denoted by
. The feasible set of (P) is denoted by
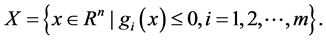
Let functions 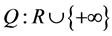 be a monotonically increasing functions satisfying
be a monotonically increasing functions satisfying
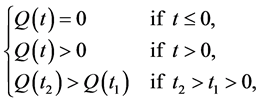
respectively. For example, 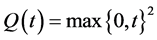 meet the requirement.
meet the requirement.
The augmented Lagrangian objective penalty function is defined as:
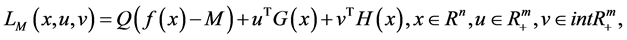 (1)
(1)
where 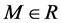 is the objective parameter, u is the Lagrangian parameter,
is the objective parameter, u is the Lagrangian parameter, 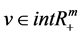 is the penalty parameter,
is the penalty parameter, 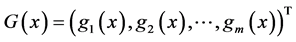 and
and 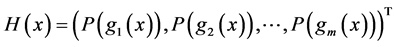 with
with 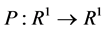 and
and
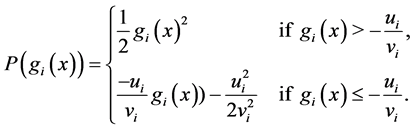
When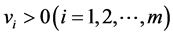 , it is clear that
, it is clear that 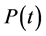 is smooth. Define functions:
is smooth. Define functions:
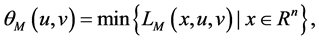 (2)
(2)
 (3)
(3)
Define the augmented Lagrangian dual problem:
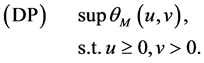
When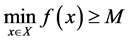
By (3), we have
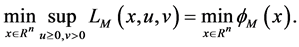
According to (1), we have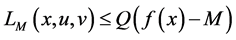
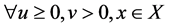
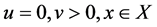
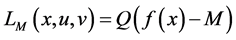
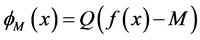
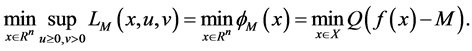
Theorem 1. Let x be a feasible solution to (P), and u,v be a feasible solution to (DP). Then
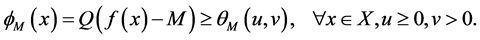
Proof. According to the assumption, we have
and
Corollary 2.1. Let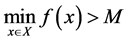
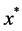
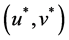
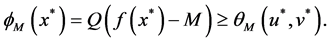
By (5), if 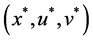
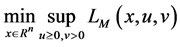
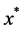

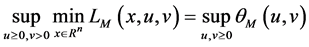
and know that 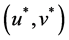
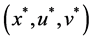
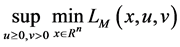
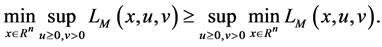
A saddle point 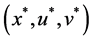
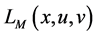
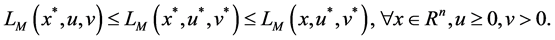
By (10), the saddle point shows the connection between the dual problem and the original problem. The optimal solution to the original problem can be obtained by the optimal solution to the dual problem and the zero gap exists in Theorem 2. The following Theorems 3 and Theorem 4 show that under the condition of convexity, saddle points are equivalent to the optimality conditions of the original problem. By (10), we have
Hence, we have the following theorems.
Theorem 2. Let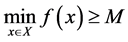
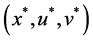
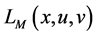
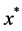
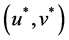
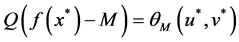
Theorem 3. Let 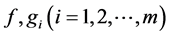
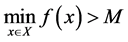
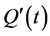
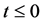
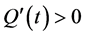
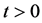
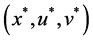
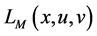
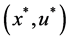
Proof. According to the assumption, 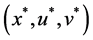
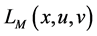
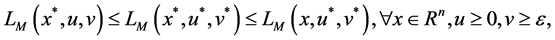
and
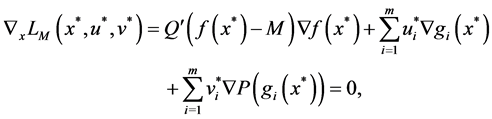
where
And there are 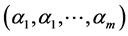
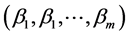
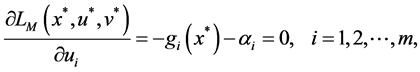
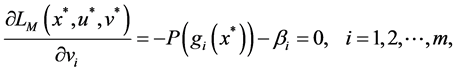
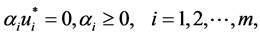
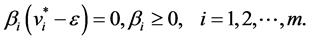
By (12)-(16), let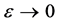
For 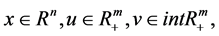
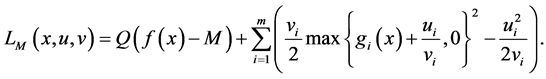
Clearly, if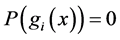
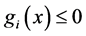
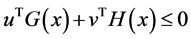
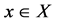
Theorem 4. Let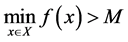
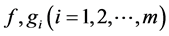
rentiable. Let 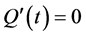
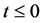
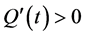
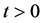
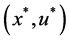
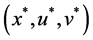
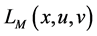
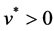
Proof. Let any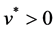
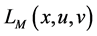
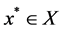
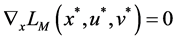
On the other hand, when 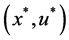
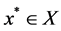
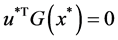
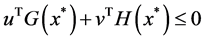
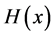
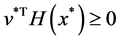
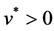
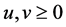
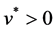
Example 2.1 Consider the problem:
When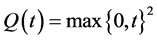
The optimal solution to 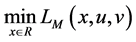
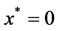
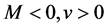
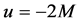
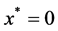
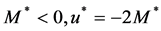
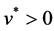
holds. Then 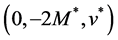
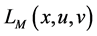
Example 2.1 shows that the augmented Lagrangian objective penalty function can be as good in terms of the exactness as the traditional exact penalty function.
For any given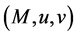
In Example 2.1, 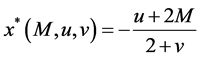
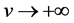
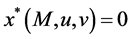
Now, a generic algorithm is developed to compute a globally optimal solution to (P) which is similar to the algorithm in [15] . The algorithm solves the problem (P(M,u,v)) sequentially and is called Augmented Lagrangian Objective Penalty Function Algorithm (ALOPFA Algorithm for short).
ALOPFA Algorithm:
Step 1: Choose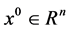
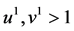
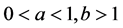
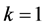
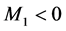
Step 2: Solve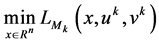
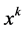
Step 3: If 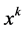
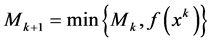
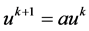
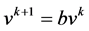
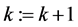
Otherwise, stop and 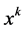
The convergence of the ALOPFA algorithm is proved in the following theorem. Let
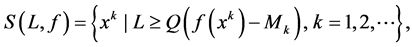
which is called a Q-level set. We say that 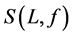
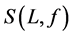
Theorem 5. Let 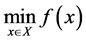
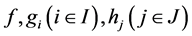
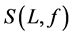
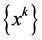
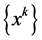
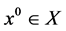
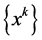
Proof. The sequence 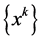
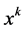
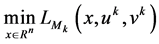
because 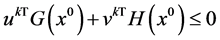
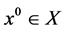
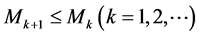
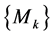
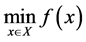
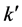
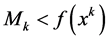
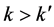
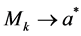
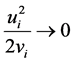
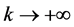
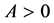
Since the Q-level set 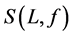
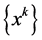
Without loss of generality, we assume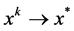
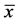
Letting 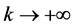
which implies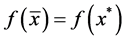
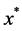
Theorem 5 means that the ALOPFA Algorithm has global convergence in theory. When v is taken big enough, an approximate solution to (P) by the ALOPFA Algorithm is obtained.
3. Conclusion
This paper discusses dual properties and algorithm of an augmented Lagrangian penalty function for constrained optimization problems. The zero gap of the dual problem based on the augmented Lagrangian objective penalty function for constrained optimization problems is proved. Under some conditions, the saddle point of the augmented Lagrangian objective penalty function i.e. equivalent to the first-order Karush-Kuhn-Tucker (KKT) condition. Based on the augmented Lagrangian objective penalty function, an algorithm is presented for finding a global solution to (P) and its global convergence is also proved under some conditions. There are still some problems that need further study for the augmented Lagrangian objective penalty function, for example, the local algorithm, exactness, and so on.
Acknowledgements
We thank the editor and the referees for their comments. This research is supported by the National Natural Science Foundation of China under Grant No. 11271329 and the Natural Science Foundation of Ningbo City under Grant No. 2016A610043 and the Natural Science Foundation of Zhejiang Province under Grant No. LY15G010007.
Cite this paper
Zheng, Y. and Meng, Z.Q. (2017) A New Augmented Lagrangian Objective Penalty Function for Constrained Optimization Problems. Open Journal of Optimization, 6, 39-46. https://doi.org/10.4236/ojop.2017.62004
References
- 1. Du, D.Z., Pardalos, P.M. and Wu, W. (2001) Mathematical Theory of Optimization. Kluwer Academic Publishers, Location.
https://doi.org/10.1007/978-1-4757-5795-8 - 2. Miele, A., Cragg, E.E., Iyer, R.R. and Levy, A.V. (1971) Use of the Augmented Penalty Function in Mathematical Programming. Part I and II. Journal of Optimization Theory and Applications, 8, 115-153.
https://doi.org/10.1007/BF00928472 - 3. Miele, A., Moseley, P., Levy, A. V. and Coggins, G.H. (1972) On the Method of Multipliers for Mathematical Programming Problems. Journal of optimization Theory and Applications, 10, 1-33.
https://doi.org/10.1007/BF00934960 - 4. Pillo, G.D. and Grippo, L. (1982) A New Augmented Lagrangian Function for Inequality Constraints in Nonlinear Programming Problems. Journal of Optimization Theory and Applications, 36, 495-519.
https://doi.org/10.1007/BF00940544 - 5. Goldfarb, D., Polyak, R., Scheinberg, K. and Yuzefobvicha, I. (1999) A Modified Barrier-Augmented Lagrangian Method for Constrained Minimization. Computational Optimization and Applications, 14, 55-74.
https://doi.org/10.1023/A:1008705028512 - 6. Lucidi, S. (1990) Recursive Quadratic Programming Algorithm That Uses an Exact Augmented Lagrangian Function. Journal of Optimization Theory and Applications, 67, 227-245.
https://doi.org/10.1007/BF00940474 - 7. Pillo, G.D., Liuzzi, G., Lucidi, S. and Palagi, L. (2003) An Exact Augmented Lagrangian Function for Nonlinear Programming with Two-Sided Constraints. Computational Optimization and Applications, 25, 57-83.
https://doi.org/10.1023/A:1022948903451 - 8. Burachik, R.S. and Kaya, C.Y. (2012) An Augmented Penalty Function Method with Penalty Parameter Updates for Nonconvex Optimization. Nonlinear Analysis, 75, 1158-1167.
https://doi.org/10.1016/j.na.2011.03.013 - 9. Morrison, D.D. (1968) Optimization by Least Squares. SIAM Journal on Numerical Analysis, 5, 83-88.
https://doi.org/10.1137/0705006 - 10. Fletcher, R. (1981) Practical Method of Optimization. A Wiley-Interscience Publication, New York.
- 11. Fletcher, R. (1983) Penalty Functions. In: Bachem, A., Grotschel, M. and Korte, B., Eds., Mathematical Programming: The State of the Art, Springer, Berlin, 87-114.
https://doi.org/10.1007/978-3-642-68874-4_5 - 12. Burke, J.V. (1991) An Exact Penalization Viewpoint of Constrained Optimization. SIAM Journal on Control and Optimization, 29, 968-998.
https://doi.org/10.1137/0329054 - 13. Fiacco, A.V. and McCormick, G.P. (1968) Nonlinear Programming: Sequential Unconstrained Minimization Techniques. Wiley, New York.
- 14. Mauricio, D. and Maculan, N. (2000) A Boolean Penalty Method for Zero-One Nonlinear Programming. Journal of Global Optimaization, 16, 343-354.
https://doi.org/10.1023/A:1008329405026 - 15. Meng, Z.Q., Hu, Q.Y. and Dang, C.Y. (2009) A Penalty Function Algorithm with Objective Parameters for Nonlinear Mathematical Programming. Journal of Industrial and Management Optimization, 5, 585-601.
https://doi.org/10.3934/jimo.2009.5.585 - 16. Meng, Z.Q., Shen, R., Dang, C.Y. and Jiang, M. (2015) Augmented Lagrangian Objective Penalty Function. Numerical Functional Analysis and Optimization, 36, 1471-1492.
https://doi.org/10.1080/01630563.2015.1070864