Open Journal of Optimization
Vol.03 No.03(2014), Article ID:49647,6 pages
10.4236/ojop.2014.33003
Efficient Combination of Topology and Parameter Optimization
Yusheng Lin, Zheng Sun, Alexandru Dadalau, Alexander Verl
Institute for Control Engineering of Machine Tools and Manufacturing Units (ISW), University of Stuttgart, Stuttgart, Germany
Email: Zheng.Sun@isw.uni-stuttgart.de
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 June 2014; revised 18 July 2014; accepted 3 August 2014
ABSTRACT
This paper presents a combination method of Particle Swarm Optimization (PSO) and topology optimization. With this method a better result can be achieved compared with the sequential application of these two optimization methods. It inherits the ability in finding global optimum from PSO and also suits for discretized design domain. Some special schemes are used in order to provide higher computation efficiency. This method has only been tested with a convex optimization problem. The application in case of a concave problem will be a future study.
Keywords:
Topology Optimization, Parameter Optimization, Combination Optimization, PSO, Structure Design

1. Introduction
Parameter optimization and topology optimization are two powerful tools in mechanical design, which affect remarkably the shape and the performance of a structure. Traditionally, the usage of these two procedures is separated and sequential. The structure is often parameter-optimized firstly, and then topology-optimized. However, the sequential method has potential insufficiencies. The general size of a structure, which is usually regarded as a design domain in topology optimization, is always changed due to the parameter optimization. The change in geometric size is sometimes useless or even conflicting as a preparation to topology optimization. In this paper, an efficient method of combined optimization is presented. It executes the parameter optimization with continuous or discretized variables and the topology optimization simultaneously, and thus achieves a better result than the sequential optimization. The paper is organized as follows: The theoretical basis of topology and parameter optimizations is introduced in Section 2. For a better presentation and explanation, an optimized case with variable bearing hole position is shown in Section 3. The implementation of the combined optimization and the methods for increasing the efficiency are proposed in Section 4. Finally, conclusion and future work are provided.
2. Theoretical Basis
2.1. Finite Element Method
The finite element method (FEM) is a numerical method that divides a domain into small connected sub-do- mains (elements), such that differential equations can be solved by solving a set of polynomial equations. With the development of computer science, more and more complicated mechanic problems in different fields are now solvable with FEM. One feature of FEM we need here is the definition of parameters for each element individually. This is important for the implementation of topology optimization, since the design variables should be set for every single element locally.
2.2. Topology Optimization
Topology optimization is a mathematical approach that optimizes the material layout within a given design space, for a given set of load and boundary conditions. It is widely used in the field of shape or structure design, especially for the lightweight design without losing much stiffness. Different kinds of topology optimization algorithms have already been carried out. Xie and Steven introduced the Evolutionary Structural Optimization (ESO) to eliminate the less effecting elements of a structure [1] [2] . Querin et al. proposed Bi-directional Evolutionary Structural Optimization (BESO) as an improvement of ESO that can also add elements in a design domain to compensate the structure defect caused by a single directional elimination of elements [3] . Bendsøe presented the Solid Isotropic Material with Penalization (SIMP) method to update the element-density-depen- dent material properties in order to reach the final optimum [4] . The penalization factor is applied to reduce the amount of intermediate densities. However, the introduction of penalization usually has a negative effect on both computational time and final results. In order to reduce such influences, Dadalau [5] introduced SIMP with an adaptive penalization scheme. In this paper the SIMP-model is used. As shown in Equation (1), it regards every element density
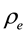 as a single optimization variable. All the variables are updated with a specific scheme which is derived by Lagrange multipliers [6] .
as a single optimization variable. All the variables are updated with a specific scheme which is derived by Lagrange multipliers [6] .
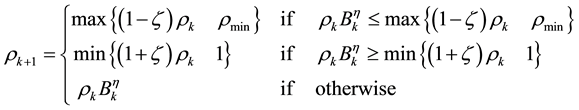 (1)
(1)
Here
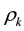 denotes the density at k-th step. Variables
denotes the density at k-th step. Variables
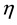 and
and
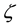 control the possible change in one iteration with the typical values of 0.5 and 0.2. This scheme adds material to the structure if
control the possible change in one iteration with the typical values of 0.5 and 0.2. This scheme adds material to the structure if
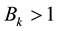 and removes it if
and removes it if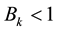 without violating the bound of
without violating the bound of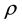 .
.
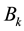 is given by
is given by
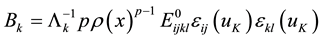 (2)
(2)
where
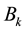 is the displacement at k-th step, which is calculated from the equilibrium function of the structure,
is the displacement at k-th step, which is calculated from the equilibrium function of the structure,
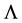 is a Lagrange multiplier and
is a Lagrange multiplier and
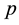 is the penalization factor.
is the penalization factor.
2.3. Parameter Optimization
Classical methods of parameter optimization, which are based on sensitivity calculation and the gradient descent method like the Newton method, are already well developed with high accuracy. However, the drawbacks are also obvious. It is expensive to calculate the needed sensitivities, if the variables are not explicit in the objective function. Moreover, in many discretized situations, the loss of continuity is usually problematic. Furthermore, the global optimum is difficult to reach, since it can be easily trapped by a local optimum. The Particle Swarm Optimization (PSO) method, known as a purpose optimization method, was originally proposed by Kennedy and Eberhart [7] . It optimizes a problem by looking for the best candidate solution in a search domain with a set of particles. The general equations for moving particles can be written as follows,
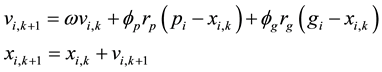 (3)
(3)
where
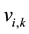 is the search velocity of i-th particle for k-th step,
is the search velocity of i-th particle for k-th step,
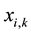 is the position of i-th particle for k-th step,
is the position of i-th particle for k-th step,





3. Problem Setting
Figure 1 shows an example case to be optimized. The length of this structure is 130, the height is 100. It has a bearing hole with a radius of 15 and the wall thickness of the hole is 10. The hole can be moved in a 51 × 51 rectangle. The structure is meshed with 2D bilinear quadrilateral elements (Q4) with an element size of 1. Thus the design domain is also discretized into 51 × 51 nodes. Along the lower half of the hole, a distributed force of 3 is added in −Y direction. At the right bottom corner, two unit forces in +X and +Y direction are applied. The left boundary is fixed in both X and Y direction.
The task is to reduce the volume by 50% and to optimize the hole position, such that the compliance is minimized. The volume of the hole is also included as a part of the deleted volume. Mathematically the optimization problem can be expressed as follows:

where







In the sequential method the best hole position is found by parameter optimization before executing the topology optimization. The final result is calculated by applying topology optimization on this hole position. The question is, whether the best position found by parameter optimization is still the best one after the topology optimization. Two enumeration tests were made as verification, which cover all the possible results in this optimi-
Figure 1.A simple structure with bearing hole to be optimized.
zation case. In the first test, the compliance of the structure is calculated with the hole position on each node of the domain without topology optimization. The value distribution is shown in Figure 2(a). The second test shown in Figure 2(b) is with topology optimization with penalization factor
As can be seen from Figure 2(a), the best hole position is located on (86, 73) before the topology optimization, which means this position would be found by the sequential method and used as the hole position for further topology optimization. And from Figure 2(b) we can easily see that the final compliance on (86, 73) is 71.51. But the optimized position from Figure 2(b) is (94, 41) with the value of 63.63, which is significantly lower than the former one. This means, at least in some cases, the results from the sequential usage of parameter and topology optimization are far from the real optimum. For this reason, we proposed a new method to find the real optimum.
4. Implementation of Combination Method
The general idea of the combination method is based on parameter optimization with the PSO method. The topology optimization is used as a way for calculating compliance, which is also the objective function of PSO. The algorithm is shown in the flowchart in Figure 3. The method is implemented with a Matlab program based on the finite element example code in [11] and the topology optimization code in [12] . However, due to the low

Figure 2. Results of the objective function raster. This is a mapping of compliance value within the design domain (zone within dash line in Figure 1). (a) stands for the compliance mapping before topology optimization while (b) stands for the one after topology optimization.
Figure 3. Flowchart of combination method.
efficiency of Matlab with its default large-scale matrix operations, the matrix storage scheme and solving method is modified according to [13] to accelerate the whole process.
In the first step, the bearing hole is set randomly on several positions. On those positions, the fast topology optimization is executed in Step 2. “Fast” means less iterations are needed to converge compared with normal topology optimization by some special schemes, which are mentioned in the following sections. The new positions are generated in Step 4 through Equation (3), until all the particles (hole positions) converge to the same position (Step 3). Finally, a slower topology optimization is applied on the global best position to achieve the optimum structure (Step 5).
4.1. Passive Element Method
The task of moving the hole position during the optimization process must be simple to handle. Normally, the empty area is not included in mesh. When the hole position is changed, meshing and assembling of the stiffness matrix need to be repeated, which decreases the efficiency greatly. This problem can be solved by the passive element method, with which the hole in the design domain can be defined as “zero” density element (
4.2. Unified Penalization Factor
The penalization factor





Due to the desired efficiency, the topology optimization during the PSO should be fast, thus the penalization factor within the fast topology optimization (Step 2 in Figure 3) is fixed to one.
4.3. Simplified Convergence Condition
The convergence condition also has a great effect on the convergence speed. Normally, the topology optimization is terminated when the largest change of the element density is smaller than a preset value [6] [12] . Under this condition, a very fine result can be achieved. Nevertheless, the change of density can fluctuate on some positions of the domain, which makes the process difficult or sometimes impossible to converge, although the change of compliance is already very small. The simplified convergence condition terminates the optimization loop, if the change of compliance is smaller than a preset value. According to Table 1, it decreases the convergence loops greatly without losing much accuracy. Through the simplified convergence condition and unity penalization, the fast topology optimization will converge in around 10 loops instead of almost 100 loops each time. Along with the flexibility of the program, the strict condition with a high penalization value can still be used to get the accurate final structure (Step 5 in Figure 3).
Table 1. Compliance and convergence speed test.
4.4. Test Results
The optimized hole position found by the combination method is converged on (93, 40) with the compliance value of 63.64, which is just one element width beside the best position of the reference (Figure 2(b)). Actually, due to the property of the PSO method, the converged result is not always the best but very close to it. Figure 4 describes the two structures after two separate steps in a sequential method. The final structure resulting from the combined method is shown in Figure 5.
5. Conclusion
In this paper, an algorithm is implemented to combine the topology optimization and PSO-based parameter optimization. Different schemes are applied to increase the computation efficiency. This algorithm was tested by an example case with a movable bearing hole. It finds the acceptable optimum result, whose compliance after the topology optimization is significantly lower than the sequential optimization. As the calculation of compliance for each position in one PSO iteration is absolutely independent, this algorithm can be easily extended to parallel computation, with which the computation speed can be further increased. It is suitable for the structure design with a convex design domain. How to extend the algorithm to the case with a concave boundary will be studied in the future.
Figure 4. Structures before and after topology optimization in sequential method. The left figure shows the actual structure after getting the best hole position by parameter optimization. The right figure is the final structure acquired by sequential method.
Figure 5. Final structure from the combination optimization.
Acknowledgements
This research is supported by the Institute for Control Engineering of Machine Tools and Manufacturing Units (ISW) and by the excellence cluster SimTech Stuttgart. This support is highly appreciated
References
- Xie, Y.-M. and Steven, G.-P. (1993) A Simple Evolutionary Procedure for Structural Optimization. Computers & Structures, 49, 885-896. http://dx.doi.org/10.1016/0045-7949(93)90035-C
- Chu, D.-N., Xie, Y.-M., Hira, A. and Steven, G.-P. (1996) Evolutionary Structural Optimization for Problems with Stiffness Constraints. Finite Elements in Analysis and Design, 21, 239-202. http://dx.doi.org/10.1016/0168-874X(95)00043-S
- Querin, O.-M., Steven, G.-P. and Xie, Y.-M. (1998) Evolutionary Structural Optimization (ESO) Using a Bidirectional Algorithm. Engineering Computations, 15, 1031-1048. http://dx.doi.org/10.1108/02644409810244129
- Bendsøe, M.-P. (1989) Optimal Shape Design as a Material Distribution Problem. Structural Optimization, 1, 192-202. http://dx.doi.org/10.1007/BF01650949
- Dadalau, A., Hafla, A. and Verl, A. (2009) A New Adaptive Penalization Scheme for Topology Optimization. Production Engineering. Research and Development, 3, 427-434. http://dx.doi.org/10.1007/s11740-009-0187-8
- Bendsøe, M.-P. and Sigmund, O. (2004) Topology Optimization: Theory, Methods and Applications. Springer Press, Berlin. http://dx.doi.org/10.1007/978-3-662-05086-6
- Kennedy, J. and Eberhart, R.-C. (1995) Particle Swarm Optimization. Proceedings of the IEEE International Conference on Neural Networks, 4, 1942-1948. http://dx.doi.org/10.1109/ICNN.1995.488968
- Shi, Y.-H. and Eberhart, R.-C. (1998) A Modified Particle Swarm Optimizer. Proceedings of the IEEE World Congress on Computational Intelligence, 69-73.
- van den Bergh, F. and Engelbrecht, A.-P. (2002) A New Locally Convergent Particle Swarm Optimiser. Proceedings of the IEEE International Conference on System Man and Cybernetics, 3. http://dx.doi.org/10.1109/ICSMC.2002.1176018
- Trelea, I.-C. (2003) The Particle Swarm Optimization Algorithm: Convergence Analysis and Parameter Selection. Information Processing Letters, 85, 317-325. http://dx.doi.org/10.1016/S0020-0190(02)00447-7
- Ferreria, A.-J.-M. (2008) Matlab Codes for Finite Element Analysis. Soild Mechanics and Its Applications Vol. 157, Springer Press, Berlin. http://dx.doi.org/10.1007/s00158-010-0594-7
- Andreassen, E., Clausen, A., Schevenels, M., Lazarov, B.-S. and Sigmund, O. (2011) Efficient Topology Optimization in Matlab Using 88 Lines of Code. Structural and Multidiscriplinary Optimization, 43, 1-16.
- Davis, T. (2000) Creating Sparse Fimite-Element Matrices in Matlab. http://blogs.mathworks.com/loren/2007/03/01/creating-sparse-finite-element-matrices-in-matlab/








