Open Journal of Optimization
Vol.03 No.01(2014), Article ID:44334,10 pages
10.4236/ojop.2014.31001
Optimal Control of an Elliptic System under Conjugation Conditions Involving Schrödinger Operator
Ahmed Mohammed Abdallah
Department of Basic Science, Higher Technological Institute, Tenth of Ramadan City, Egypt
Email: abdallaham6236@yahoo.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 January 2014; revised 19 February 2014; accepted 4 March 2014
ABSTRACT
The purpose of this paper is to study the optimal control of the n × n cooperative elliptic system with variable coefficients under conjugation conditions and mixed boundary condition involving Schrödinger operator defined on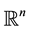 . By using Green’s formula, properties of the first Eigen values and Lax-Milgram lemma, we prove the existence and uniqueness of solutions for these Systems. We also study the necessary and sufficient conditions for having a maximum principle and existence of solution for the given linear elliptic system.
. By using Green’s formula, properties of the first Eigen values and Lax-Milgram lemma, we prove the existence and uniqueness of solutions for these Systems. We also study the necessary and sufficient conditions for having a maximum principle and existence of solution for the given linear elliptic system.
Keywords:
Elliptic Systems; Existence and Uniqueness of Solutions; Conjugation Conditions; Mixed Boundary Condition; Schrödinger Operator; Optimal Control

1. Introduction
The necessary and sufficient conditions of optimality for systems governed by elliptic operators have been studi- ed by Lions in [1] . Optimal control problems of distributed systems that include partial differential equations have many mechanical sources and a variety of technological and scientific applications. Much optimal control problems of elliptic systems involving Schrödinger operators have been studied in [2] [3] . The linear quadratic optimal control problem described by a distributed parameter system has a variety of mechanical and technical sources and applications. In this paper, we obtain some necessary (sufficient) conditions for the validity of ma- ximum principle cooperative elliptic systems.
2. Distributed Control of an Elliptic System with Conjugation Conditions Involving Schrödinger Operator
2.1. The Case of 2 × 2 Elliptic Systems with Conjugation Condition and Mixed Boundary Condition
In this section, we consider the following 2 × 2 elliptic system (see [3] [4] )
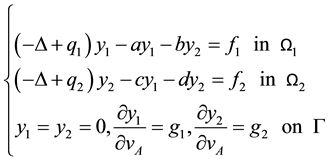 (1)
(1)
where 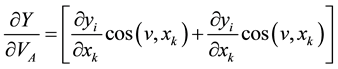 on Γ,
on Γ, 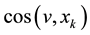 = K-the direction cosine of v, v being the normal on the Γ exterior to Ω and
= K-the direction cosine of v, v being the normal on the Γ exterior to Ω and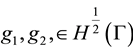 ,
, 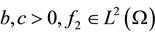
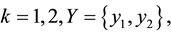 ,
, 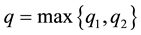 and conjugation conditions (*)
and conjugation conditions (*)
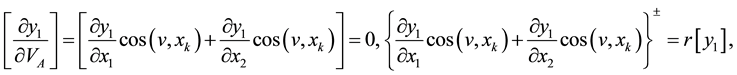
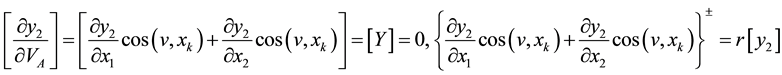 ,
,
where Ω is an open subset of 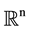 with smooth boundary
with smooth boundary 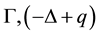 is Schrödinger operator,
is Schrödinger operator, 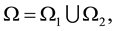
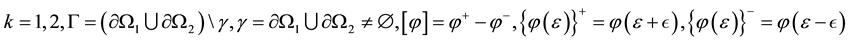 . The giv-
. The giv-
en elliptic equation is specified in bounded, continuous and strictly Lipschitz domains in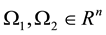 .
.
2.1.1. Existence and Uniqueness of Solution
Since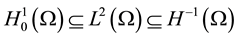 , Then we have chain of the form
, Then we have chain of the form
we define the following bilinear form on
Lemma 1(see [3] )
Let



Lemma 2(see [3] )
First Eigen values 
For 

Theorem 1
For

The bilinear form can be written as
We choose m large enough such that a + m > 0 and d + m > 0 and the equivalent norm
By Cauchy Schwartz and Lemma 1 and 2 in the paper




tion


2.1.2. Formulation of the Control Problem
Let 
The energy functional

A unique state

are specified on domain 




The observation equation is given by
The cost functional is given by:

where



The control problem then is to find:

where 

where

Assume that (2), (6) hold. The cost function being given (5), necessary and sufficient for u to be an optimal control is that the following equations and inequalities be satisfied


Outline of proof
Since 



Since 
then
By Green’s formula or derivative in the sense of distribution
where 




From (7), we obtain
Remark 1
Generalization to n × n systems
and conjugation conditions

where 






In this case, the bilinear form is given by:
The linear form is given by:
The cost functional is given by:
where 



on 
In this case the necessary and sufficient for u to be an optimal control is that the following equations and inequalities be satisfied.


If constraints are absent i.e. when 

problem of finding the vector-function

We can find last relations at 
We can choose 
3. Boundary Control of an Elliptic System with Conjugation Conditions Involving Schrödinger Operator
Formulation of the Control Problem
Let 
For a control 


The observation equation is given by
Since the cost function (5) can be written as:
where
since 


The necessary and sufficient for u to be an optimal control is that the following equations and inequalities be satisfied


Outline of proof
Since J(v) is differentiable and Uad is bounded then the optimal control u is characterized 


Since 
then
By Green’s formula or derivative in the sense of distribution
where 

From (6), we obtain
We can add the control in the part of Dirichlet condition, i.e.

The difference appears in characterization
Remark 2
Generalization to n × n systems
and conjugation conditions

where Ω is an open subset of 



terior to Ω,

In this case, the bilinear form is given by:
The linear form is given by
The cost functional is given by:

where 



on 

In this case the necessary and sufficient for u to be an optimal control is that the following equations and inequalities be satisfied.



If constraints are absent i.e. when 

problem of finding the vector-function

We can find last relations at n = 2 and q = 0 [7] .
4. Conclusion
The aim is to find the existence and uniqueness of solution (state of the system) and necessary and sufficient condition for optimality of the system in 2 × 2 and generalization to n × n in the case of distributed and bounda- ry control. In this paper, we connect [3] with [4] to get a new work with following the developments.
References
- Lions, J.L. (1971) Optimal Control of a System Governed by Partial Differential Equations. Springer-Verlag Band, New York. http://dx.doi.org/10.1007/978-3-642-65024-6
- Serag, H.M. (2000) Distributed Control for Cooperative Systems Governed by Schrödinger Operator. Journal of Discrete Mathematical Science and Cryptography, 3, 227-234. http://dx.doi.org/10.1080/09720529.2000.10697910
- Serag, H.M. and Qamlo, A.H. (2005) On Elliptic Systems Involving Schrodinger Operators. The Mediterranean Journal of Measurement and Control, 1, 91-96.
- Deineka, V.S. and Sergienko, I.V. (2004) Optimal Control of an Elliptic System with Conjugation Conditions and Neu- mann Boundary Conditions. Cybernetics and Systems Analysis, 40, 865-882. http://dx.doi.org/10.1007/s10559-005-0026-7
- Gali, I.M. and Serag, H.M. (1994) Distributed Control of Cooperative Elliptic Systems, the UAB. Georgeatrch International Conference on D.E. and Mathematical Physics, Birmingham, 1994.
- Deineka, V.S. and Sergienko, I.V. (2001) Models and Methods for Problem Solution in Heterogeneous Media. Kyiv (in Russian), Naukova Dumka.
- Qamlo, A.H. and Bahaa, G.M. (2013) Boundary Control for 2 × 2 Elliptic Systems with Conjugation Condition. Intelligent Control and Automation, 4, 280-286.








































