International Journal of Modern Nonlinear Theory and Application
Vol.2 No.4(2013), Article ID:40272,6 pages DOI:10.4236/ijmnta.2013.24027
Non-Topological Solitons as Traveling Pulses along the Nerve
Instituto Literario, Facultad de Ciencias, Universidad Autonoma del Estado de Mexico, Toluca, México
Email: maaguerog@uaemex.mx
Copyright © 2013 Fidel Contreras et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received October 2, 2013; revised November 2, 2013; accepted November 9, 2013
Keywords: Dark Solitons; Bubbles; Nerve Pulses; Nonlinear Waves; Density Waves
ABSTRACT
Several new soliton-like structures have been obtained under the consideration of non trivial boundary condition for the difference value of density in the thermodynamic model of nerve pulses. The model is based on thermodynamic principles of zero transfer of energy to the media. We have studied these solutions for particular values in the parameter space, and obtained both bell soliton on the condensate and bubble like solutions as typical non-topological representative solutions. The solutions will propagate along the nerve with constant velocity. The analysis of the properties of the solutions provides us with available permitted velocities and the prediction of the constant density value of the background at long distances far from the excited zone in the nerve.
1. Introduction
As it is well known, the nature of the mechanisms for propagation signals along the nerve is one of the crucial problems in nonlinear biophysics. There are several approaches that treat of the propagation of nerve pulses with the insertion of electric potential signals, for example. According to a great number of investigations concerning the complex dynamics of the ionic currents through voltage sensitive channels, the first detailed measurements of these currents were carried out by Hodgkin and Huxley in the 50 s [1]. After these findings were presented, Katz [2] proposed the solitonic type of transmitting signals along the nerves. By introducing an approximate scheme to the famous model of Hodgkin— Huxley, Nagumo and FitzHugh proposed a simplified neuronal model on the basis of a nonlinear electric circuit controlled by an equation system also similar to Van Der Pol currents [3,4] and constituted a classical model of neurophysiology. By using an analytic technique, the homotopy analysis method (HAM) in the FitzHugh-Nagumo (FHN) equation, Abbasbandy [5] has found solitary wave solutions which are subjected to the control of new auxiliary parameter. Being susceptible to fairly complete analysis, the FHN system allows a qualitative understanding of the phenomenon of excitability, from the point of view of dynamical systems [6].
Despite these quite interesting findings, surprisingly, Heimburg and coworkers proposed another type of model based on the density excitation of nerve membranes. The phase transition in membranes has been studied in the work [7]. They have further developed their model for nerve pulses that supports several classical soliton-like solutions [8-10]. The model is constructed to consider the nerve axon as a dimensional cylinder with lateral density excitations, moving along the axes, represented by the coordinate z. This alternative model for the nerve pulses is based on the propagation of a localized density pulse (non linear wave) in the axon membrane and shows the appearance of a lipid phase transition slightly below physiological temperatures. Given measured values of the compression modulus as a function of lateral density and frequency, soliton properties can be determined by the velocity of the traveling waves. In summary, we can say that this theory is based on the lipid transition from a fluid to a gel phase at slightly below body temperature. The effects of nonlinearity and dispersion, as it is common, would be responsible for the appearance of soliton-like structures in nerve membrane in the gel state [11].
We suppose that along the axon, not only the wellknown “bell” solitons on zero background could propagate, but also, that it is highly likely, we can find nontopological bubble and bright soliton-like solutions that could propagate with constant velocity along the axon on a nonzero density background. The bubble or rarefaction structure and soliton on the background would propagate along the excited background of the nerve membrane. As it is known, bubble solitary waves are ubiquitous nonlinear excitations of dispersive wave models. In the literature there are several names for this type of solutions such as gray or dark solitons. We will keep calling them as bubble solitons that were used prolifically by Makhankov et al. [12]. In a general scope, these excitations consist of a density dip (i.e., a dark notch) on a background of constant value field. These nonlinear traveling waves could be responsible for conserving and a posteriori efficiently transmitting the necessary information along the axons. The appearance of bubble and bright solitons on the background is not new: in many branches of physics [13-16] the bubble solitons play a crucial role. Numerous experiments and theoretical studies have demonstrated the emergence of these nonlinear states for example in optics [17] with the so-called self-defocusing nonlinearity, in BEC systems [18] among others. As it is well known, these structures live in the “false” vacuum of the potential piece of the energy for the mechanical analog problem.
Thus, we study the model of Heimburg and coworkers [9] and by applying the non-trivial or condensate boundary condition, we found non-topological soliton like solutions of two types: the bubble and solitons on condensate (pedestal like solitons). In the next section we briefly expose the main nonlinear evolution equation and its weak formulation for nerve pulses. In section III the bubble and other soliton-like solutions with non trivial boundary condition are studied. Section IV is devoted to discussing the super and subsonic bubble and anti bubble solutions. In section V we briefly expose the stability of the background that serves as a background of the nontopological solitons and finally, in the last section we discuss some features surrounding the solutions found and outline further implications of the model presented.
2. “Thermodynamic” Equation of Motion for Nerve Pulses
The detailed discussion on methods and proposals for obtaining the nonlinear differential equation which is the subject of our analysis, can be found in the appropriate literature, see for example [8,9]. Here we outline some basic principles of the theory based on hydrodynamic properties of a density pulse in the presence of dispersion. The analysis carried out in the mentioned works, started with the classic sound propagation equation in the absence of dispersion along the quasi-unidimensional axon for the fundamental difference 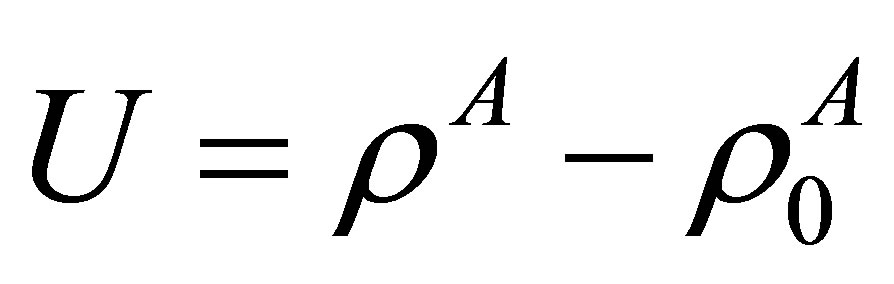 being the change of density in the membrane. Here
being the change of density in the membrane. Here 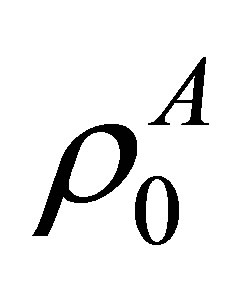 is the density of the membrane at physiological conditions slightly above melting transition. The excitations move along the coordinate
is the density of the membrane at physiological conditions slightly above melting transition. The excitations move along the coordinate  at the time
at the time . Next, the parameter
. Next, the parameter 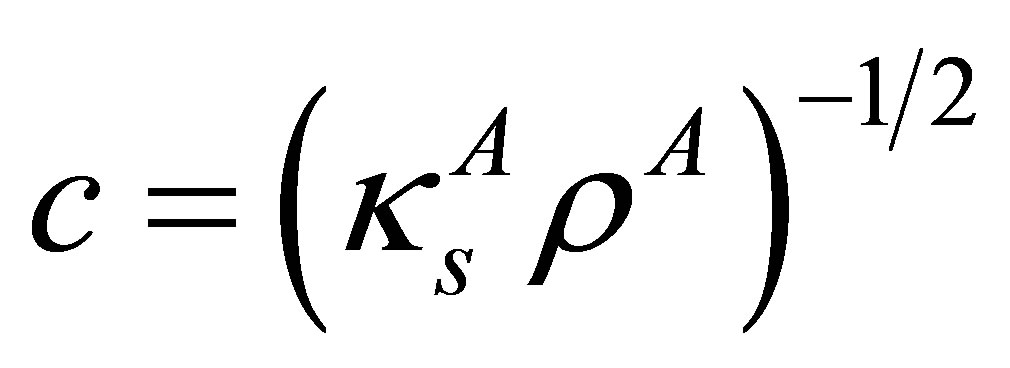 with
with 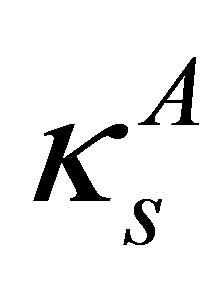 being the compressibility, evolves in dependence on the unknown ”field”
being the compressibility, evolves in dependence on the unknown ”field”  in a similar fashion to the Kerr Effect in nonlinear optics (Nerve Kerr effect in biomembranes?).
in a similar fashion to the Kerr Effect in nonlinear optics (Nerve Kerr effect in biomembranes?).
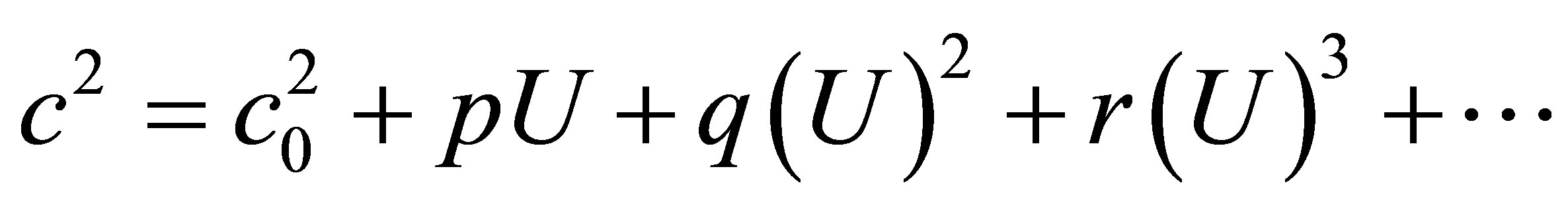 (1)
(1)
with 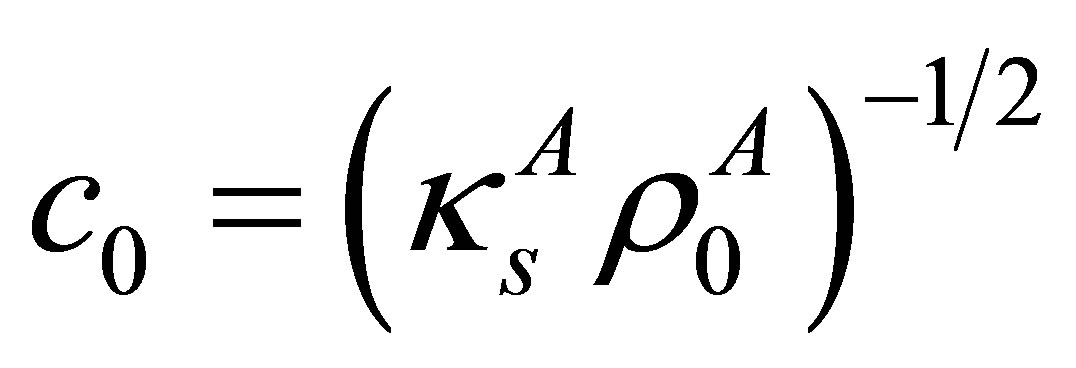 being the small sound velocity.
being the small sound velocity.
An important justification for the assumption of an electromechanical process is the experimental observation of reversible heat changes in phase with the action potential and a zero net heat release during the action potential [9]. Finally, the equation of motion of density waves along the axon can be represented by [8,9]:
 (2)
(2)
In this paper we will consider that far from the excited zone along the axon, the difference density 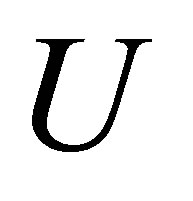 remains constant i.e. it is not completely equal to zero. Thus, for this case, the nontrivial boundary condition is considered, and it affects the subsequent evolution of nonlinear waves.
remains constant i.e. it is not completely equal to zero. Thus, for this case, the nontrivial boundary condition is considered, and it affects the subsequent evolution of nonlinear waves.
Weak Formulation
Before the application of the boundary condition we slightly modify the Equation (2) bearing in mind the traveling wave solution with the independent variable . By integrating the Equation (2) it can be transformed to the following one
. By integrating the Equation (2) it can be transformed to the following one
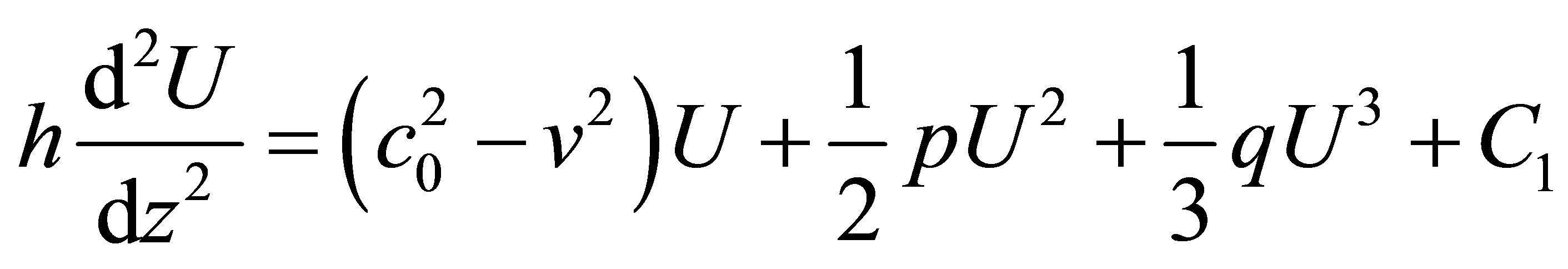 (3)
(3)
here  is a constant that is obtained after integration. After subsequent integration one can obtain the next equation
is a constant that is obtained after integration. After subsequent integration one can obtain the next equation
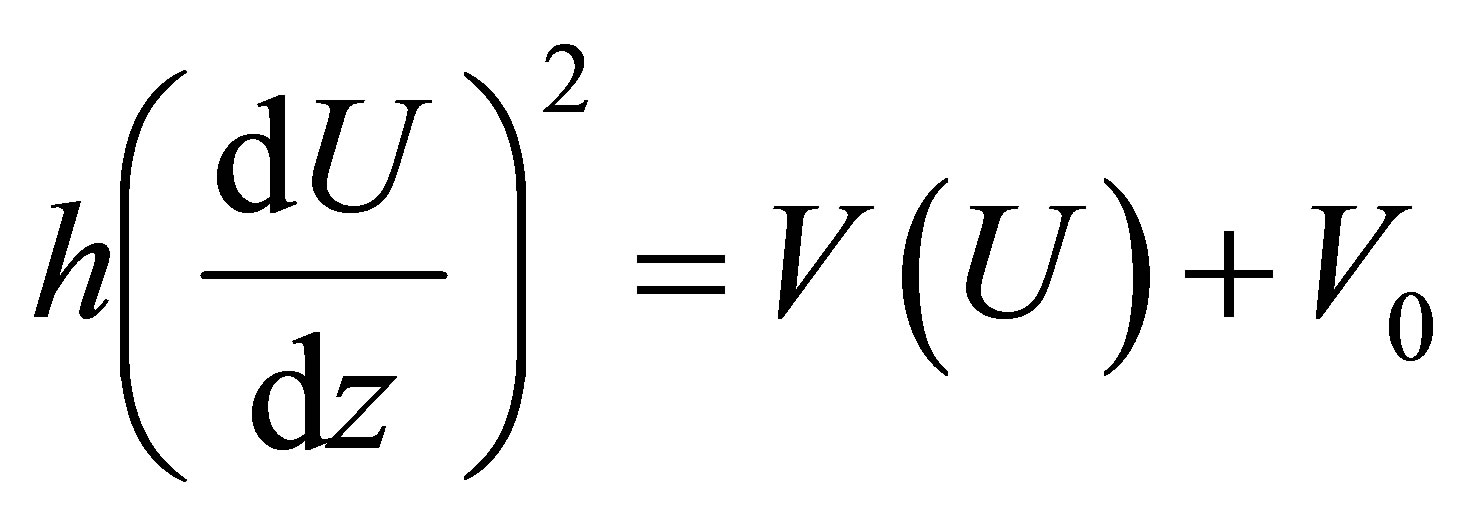 (4)
(4)
with
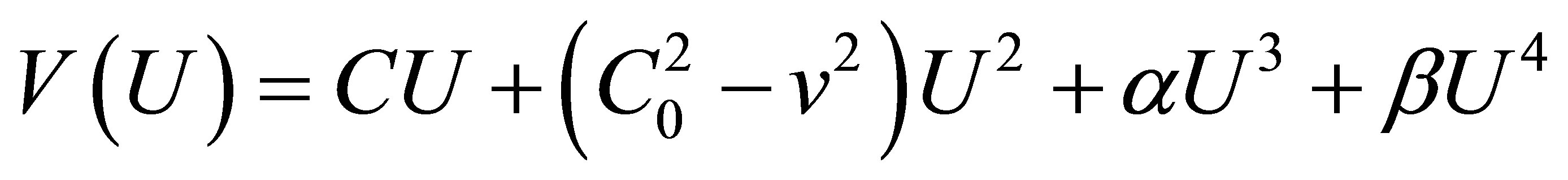
and
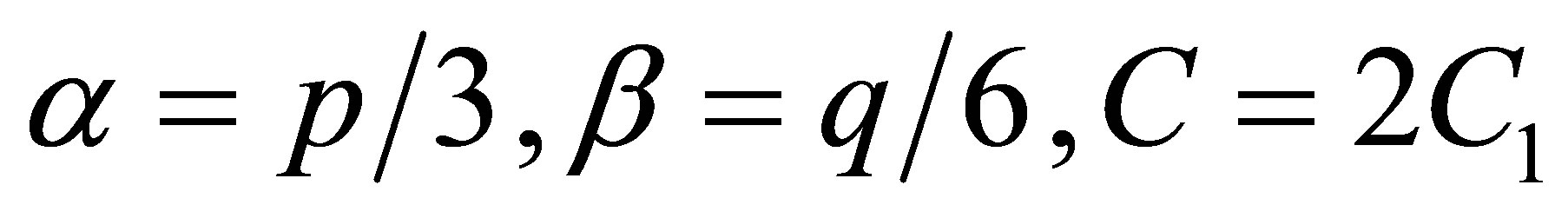 (5)
(5)
being  and
and 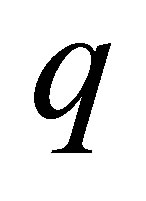 the parameters that appear in the Taylor expansion (1). The parameters
the parameters that appear in the Taylor expansion (1). The parameters 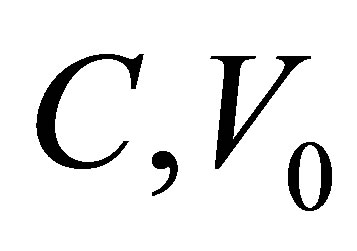 are the constants of integration for the first and second integration correspondingly. For the Equation (4) to make sense in terms of distribution it is enough that
are the constants of integration for the first and second integration correspondingly. For the Equation (4) to make sense in terms of distribution it is enough that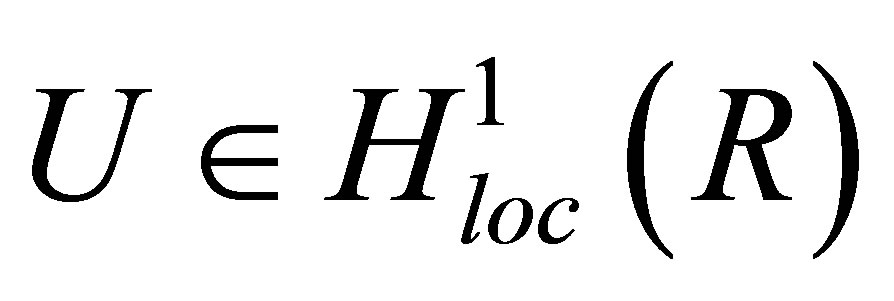 .
.
3. Traveling Non-Topological Structures in the Model
Now let us study the Equation (4) by keeping in mind the non-trivial or the condensate boundary condition, that means at long distances from the main excited zone of the axon, the perturbation pulse does not vanish while its first derivative tends to zero. Thus, the unknown function 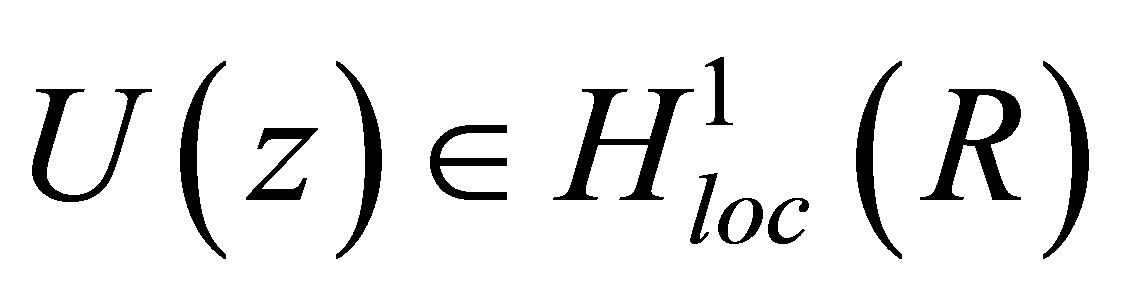 in the distributional sense satisfies
in the distributional sense satisfies
 (6)
(6)
By applying this restriction, the constants of integration 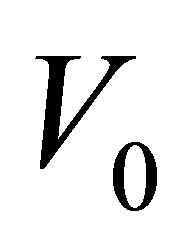 and
and  satisfy the next equation
satisfy the next equation
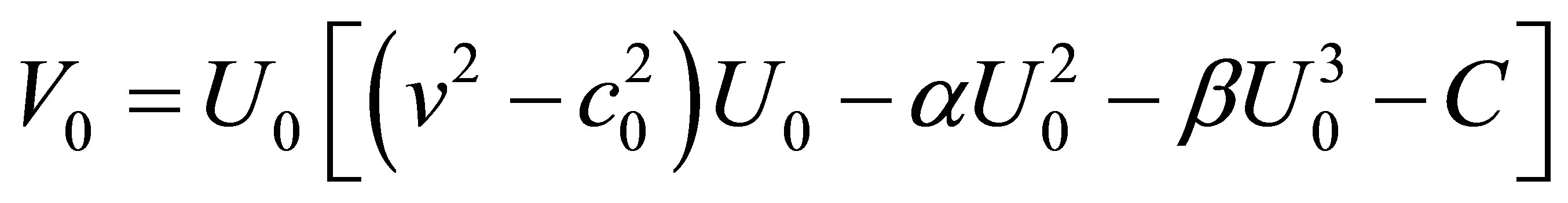 (7)
(7)
As it can be easily seen this constant of integration depends on the background value of the difference density 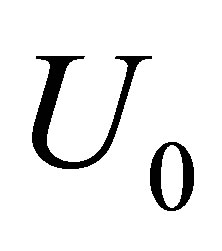 which far from the excited zone will remain unperturbed.
which far from the excited zone will remain unperturbed.
Traveling Sonic Solution
First, let us consider the case: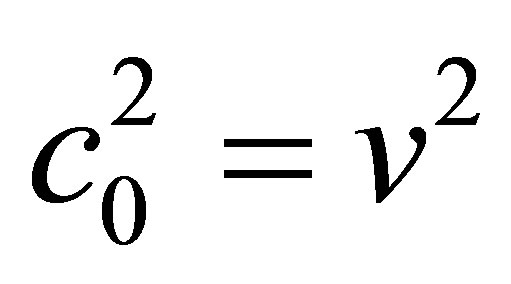 , when the nonlinear wave will move with the sound velocity along the axis
, when the nonlinear wave will move with the sound velocity along the axis . Analyzing the possible consequences of this reduction, one can find that the right hand side of the Equation (4) could be transformed in such a way that this equation after integration will take the following form
. Analyzing the possible consequences of this reduction, one can find that the right hand side of the Equation (4) could be transformed in such a way that this equation after integration will take the following form
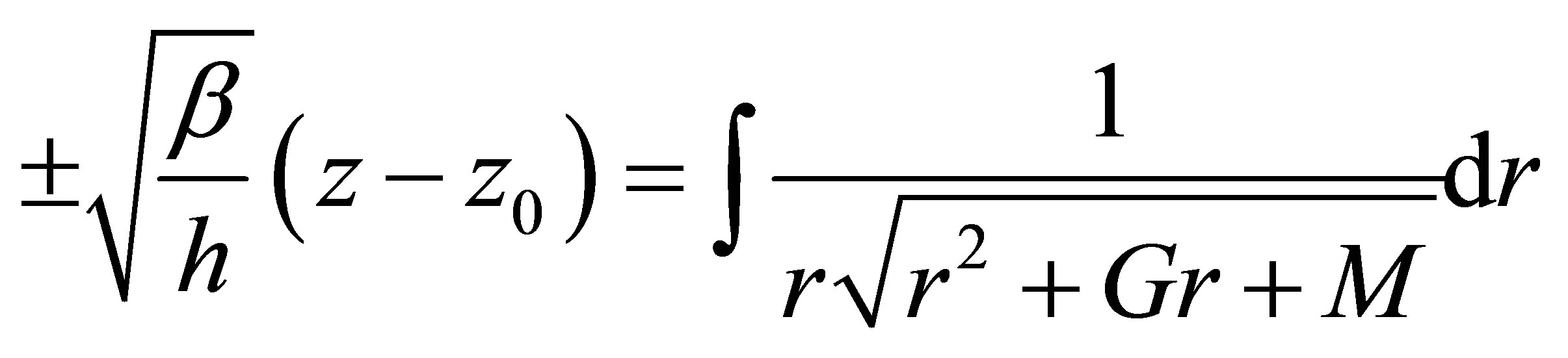 (8)
(8)
with
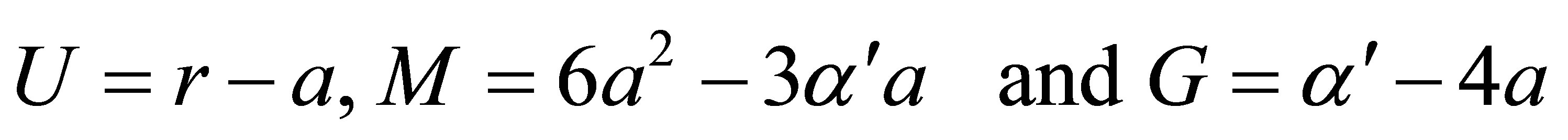 (9)
(9)
and  where the parameter
where the parameter  needs to satisfy the algebraic cubic equation
needs to satisfy the algebraic cubic equation
 (10)
(10)
For solving this cubic algebraic equation (10) we need to calculate de discriminant
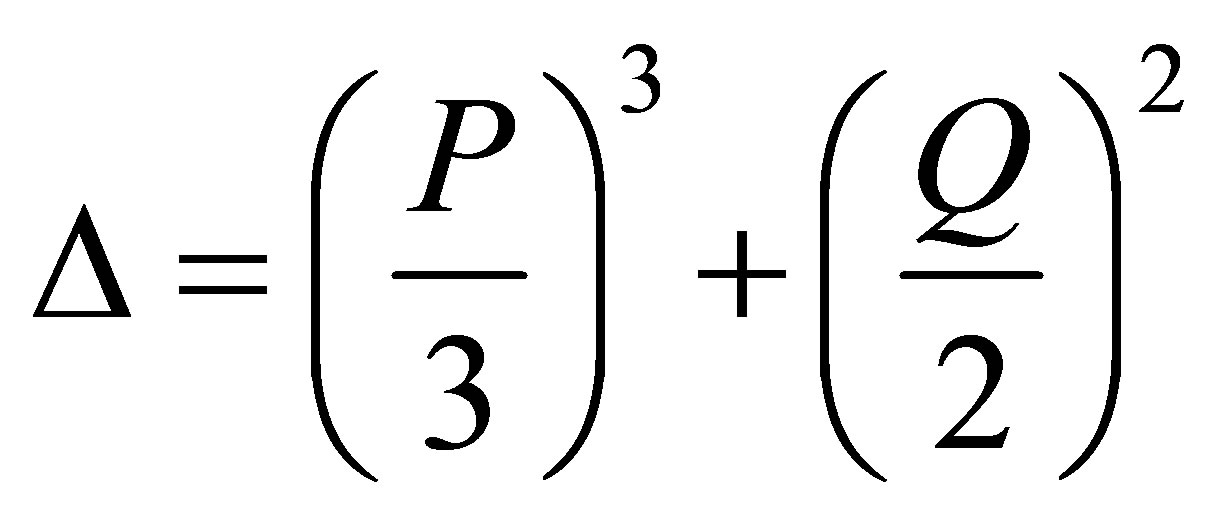 (11)
(11)
with  and
and 
After the necessary algebra we obtain
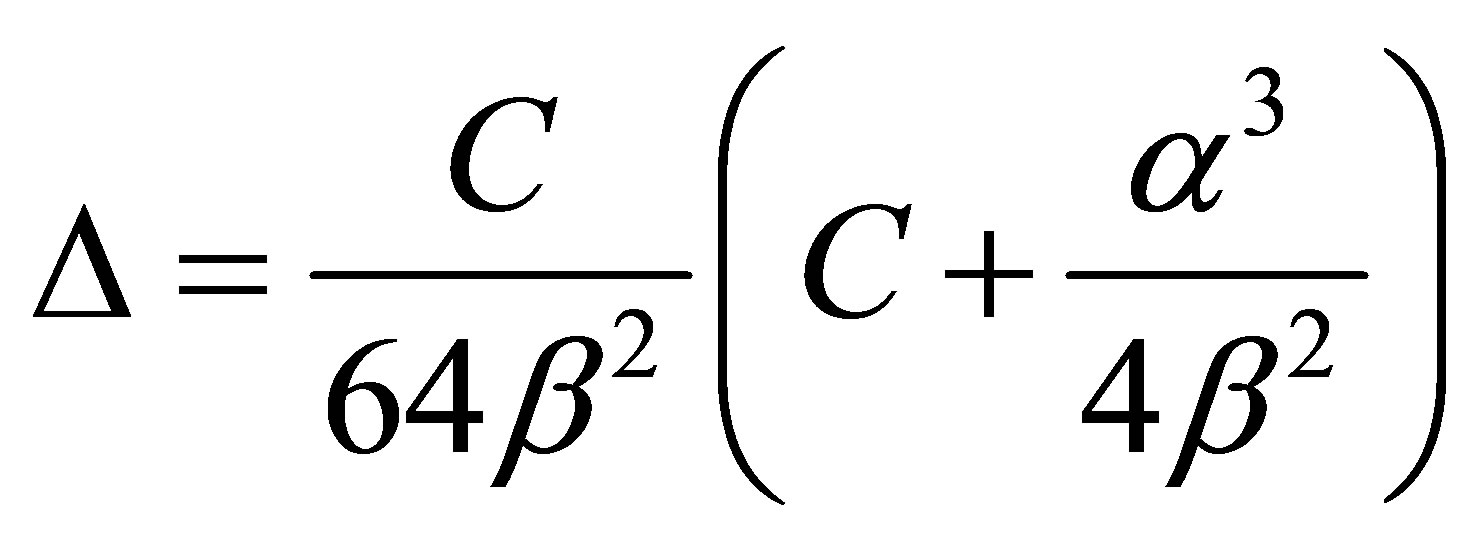 (12)
(12)
As it is well known the Cardano type of solutions for the algebraic cubic equation are determined by the discriminant . The cubic equation has one real and two conjugate complex roots, three real roots of which at least two are equal or two different real roots, if
. The cubic equation has one real and two conjugate complex roots, three real roots of which at least two are equal or two different real roots, if  is positive, zero, or negative, respectively. By analyzing each possibility one can conclude that the case of zero value of
is positive, zero, or negative, respectively. By analyzing each possibility one can conclude that the case of zero value of  will be dropped because the potential piece of the energy in this case does not support additional relative minimum. Thus, we can use either the case
will be dropped because the potential piece of the energy in this case does not support additional relative minimum. Thus, we can use either the case  or
or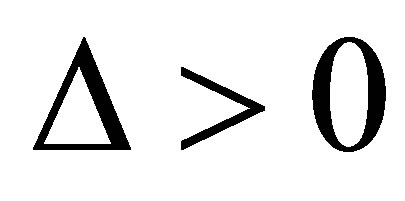 . For concreteness we could use the case when
. For concreteness we could use the case when  is positive, as a valuable example. If this is the case, then we have one real root and two conjugate complex roots. Consequently one obtains for the real root
is positive, as a valuable example. If this is the case, then we have one real root and two conjugate complex roots. Consequently one obtains for the real root
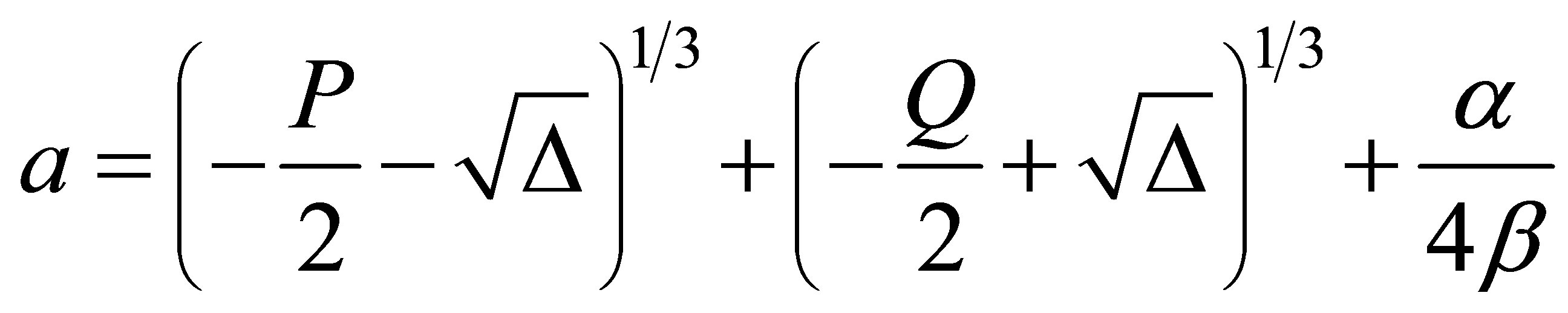 (13)
(13)
and
 (14)
(14)
Having obtained the value of parameter  from the cubic Equation (10), it should be easy to calculate the value of parameter
from the cubic Equation (10), it should be easy to calculate the value of parameter 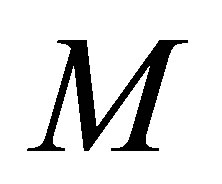 by using Equation (9). In order to integrate the Equation (8) and obtain analytical and nonsingular solutions we impose the condition for the discriminant of the expression under the square in the Equation (8) as follows
by using Equation (9). In order to integrate the Equation (8) and obtain analytical and nonsingular solutions we impose the condition for the discriminant of the expression under the square in the Equation (8) as follows
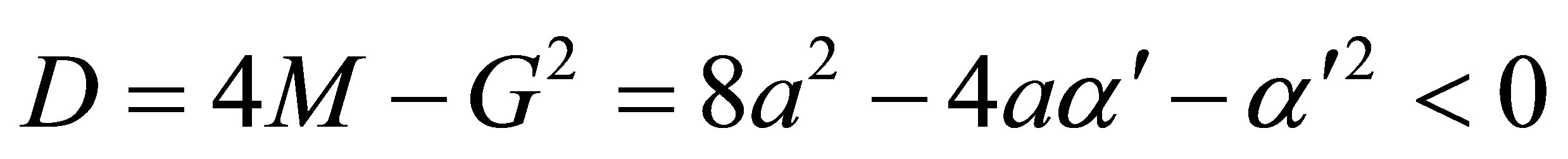 .
.
Under all these requirements we can make an assumption that regular localized soliton-like solutions exist when the parameters 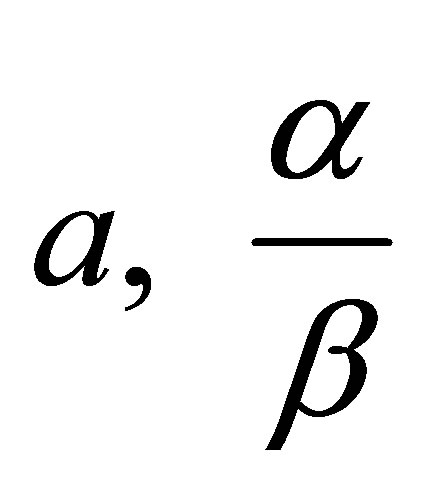 satisfy whichever of these two inequalities
satisfy whichever of these two inequalities
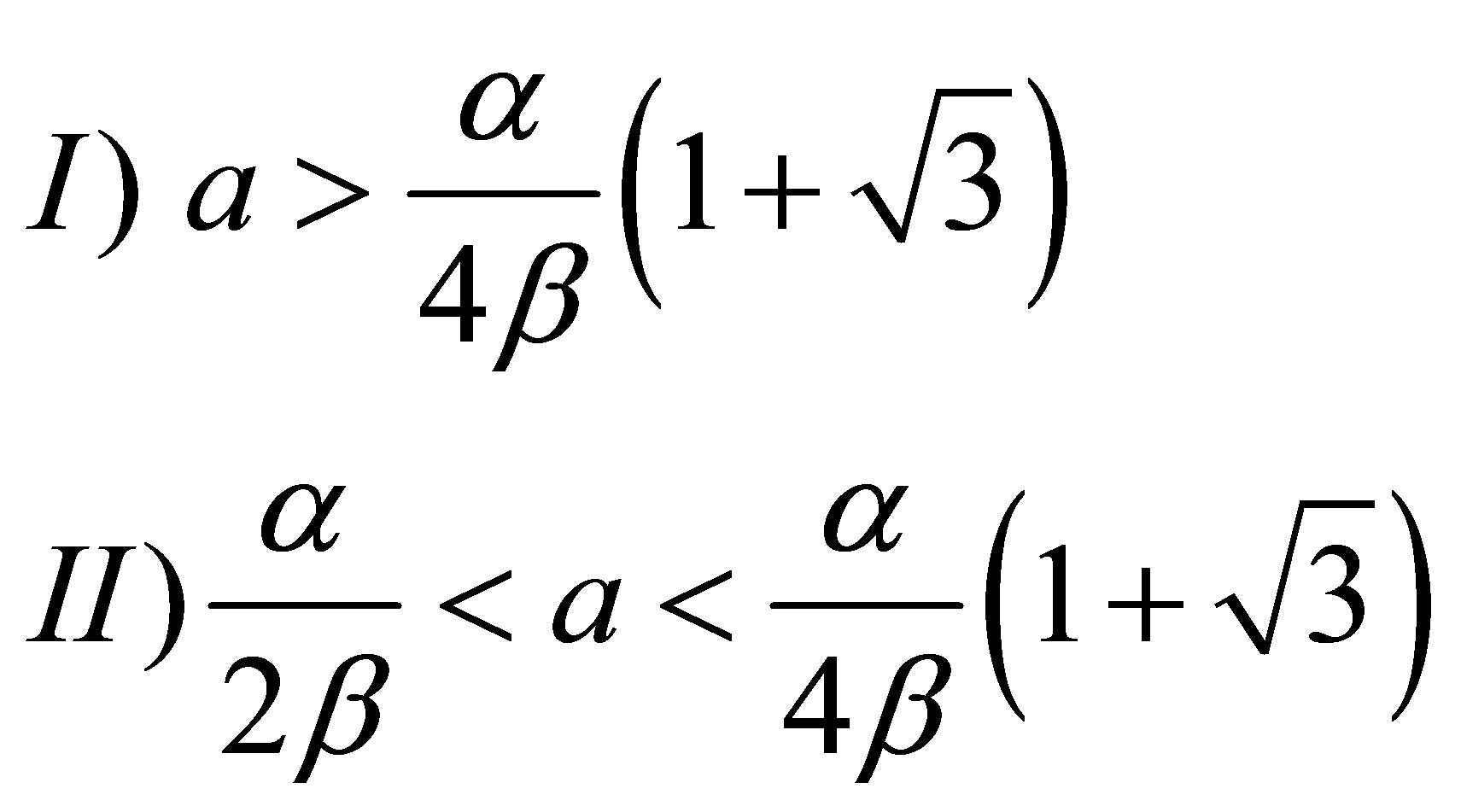 (15)
(15)
These parameter restrictions will be the conditions for the existence of a set of non-topological solitons.
By inverting the integral (8) written above, one has finally the following solution by avoiding singular behavior
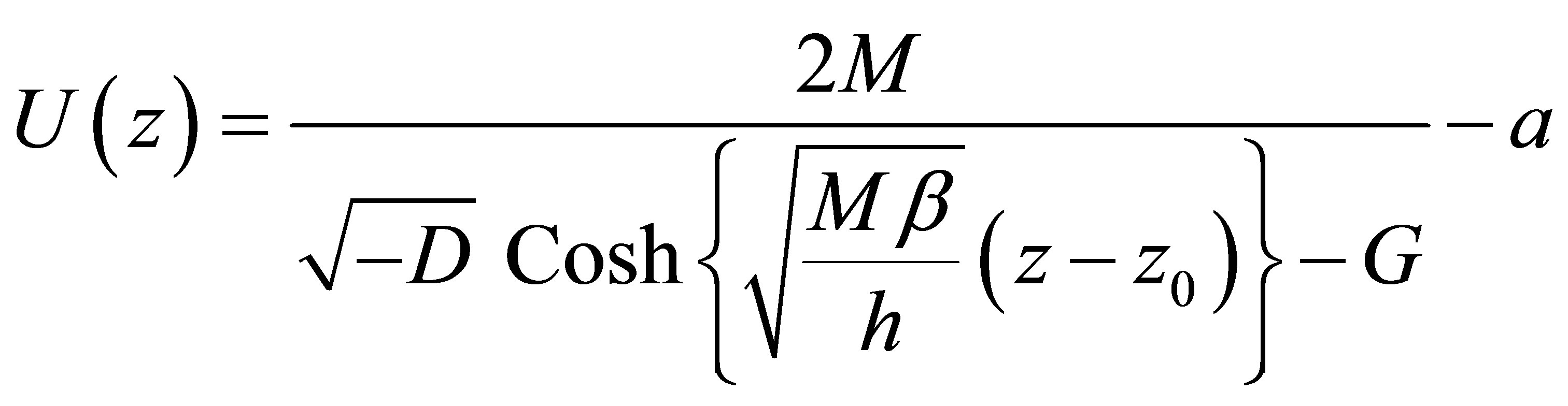 (16)
(16)
As usual, for qualitative purposes, this solution can be visualized by taking concrete parameter values. For instance, for a good picture presentation let us suppose that 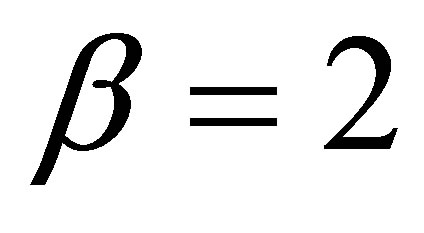 and, according to the work [10] for unilamellar DPPC vesicles, we can take for example the value
and, according to the work [10] for unilamellar DPPC vesicles, we can take for example the value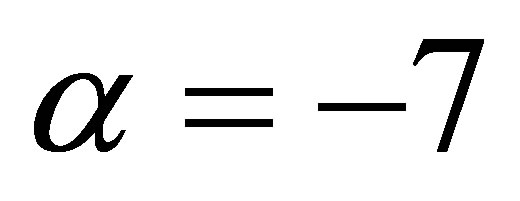 . Thus, the other important parameters should estimate straightforward, and after reparameterization of variables finally the resulting picture of a soliton on background is depicted in Figure 1.
. Thus, the other important parameters should estimate straightforward, and after reparameterization of variables finally the resulting picture of a soliton on background is depicted in Figure 1.
4. Super and Sub-Sonic Traveling Non-Topological Solutions
Let us now investigate the other case when the values of the velocities of traveling structures are different than the sound one. We replace the value 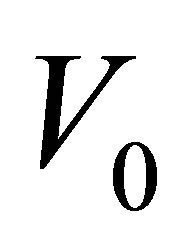 of Equaiton (7) in the Equation (4) and obtain for
of Equaiton (7) in the Equation (4) and obtain for 
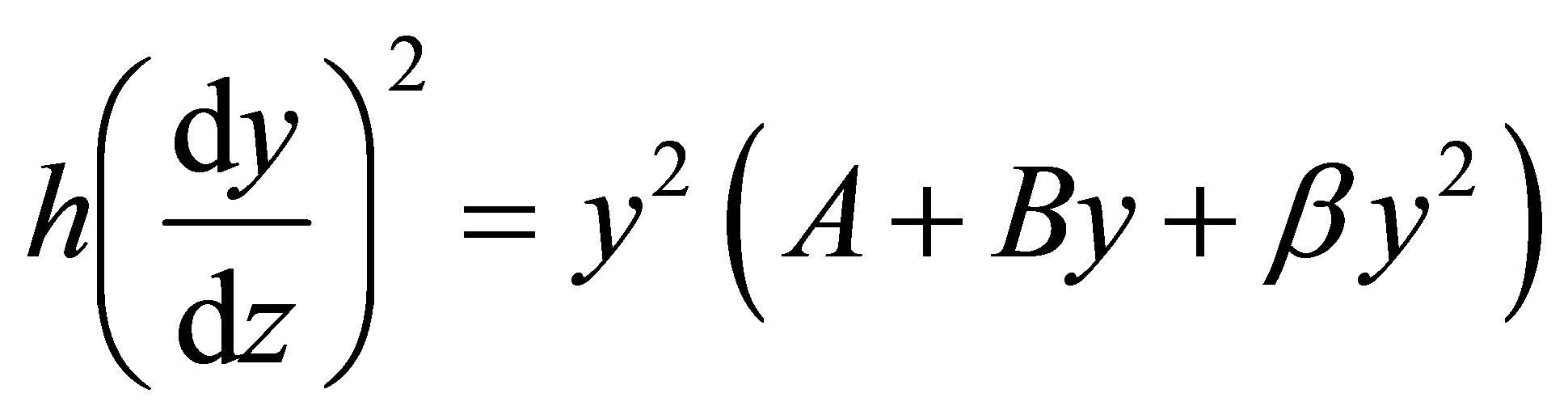 (17)
(17)
This equation is obtained considering the following relations of the parameter values:
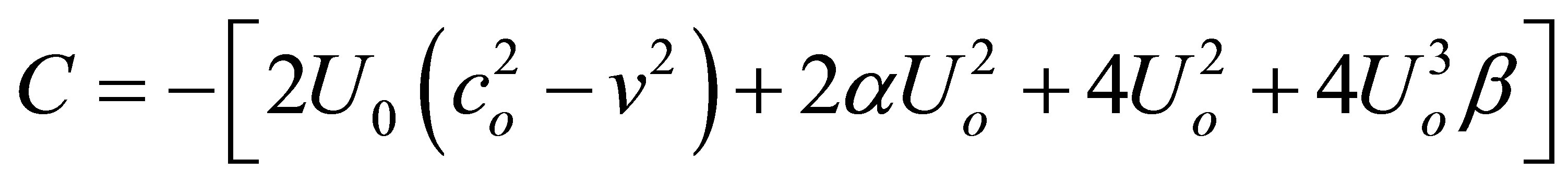 (18)
(18)
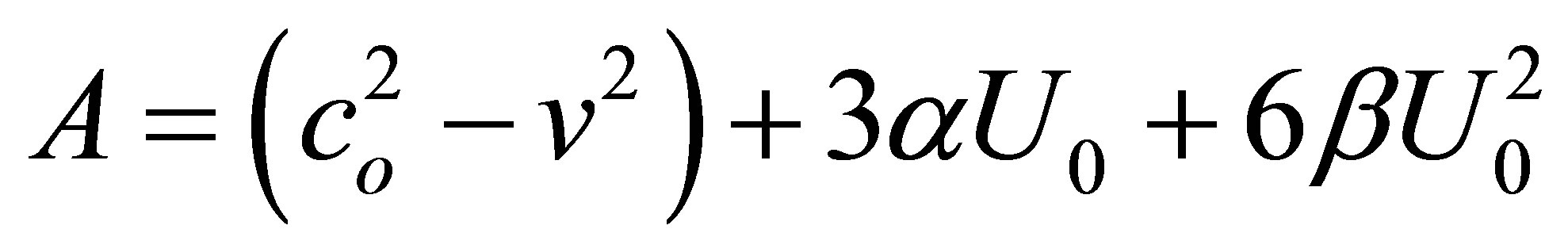 (19)
(19)
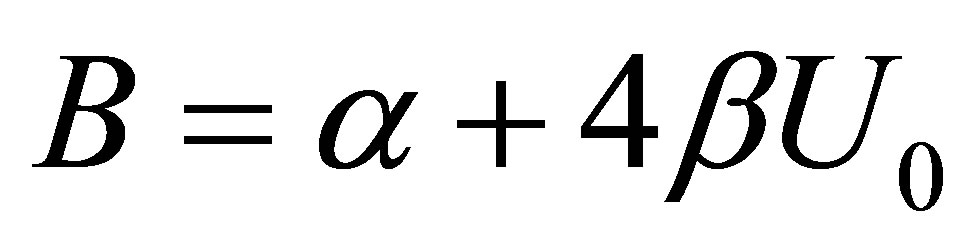 (20)
(20)
To avoid singular behavior, let us suppose that parameters ,
,  and
and  satisfy the next inequalities
satisfy the next inequalities
 (21)
(21)
Thus, after the corresponding integration we have obtained
 (22)
(22)
Again  should take only negative values for avoiding singularities in the solution (22) and it can be completely satisfied because of the availability for negative and positive values of
should take only negative values for avoiding singularities in the solution (22) and it can be completely satisfied because of the availability for negative and positive values of . Thus the parameters
. Thus the parameters ,
,
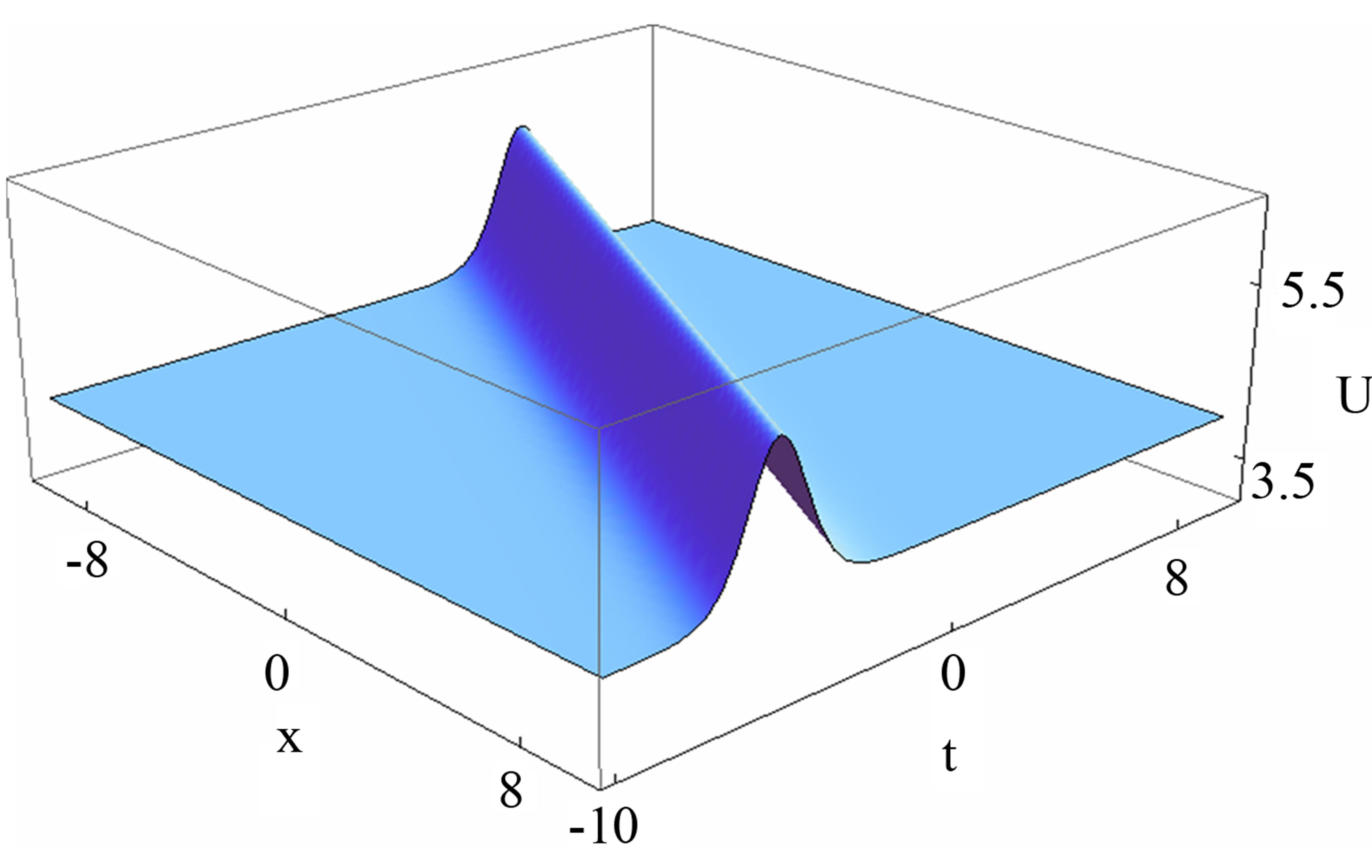
Figure 1. Typical “bright” soliton on background traveling with the same velocity of sound along the axon. Its existence is due to the manifestation of the relative minimum (the “false vacuum”) in the potential piece of the energy in the mechanical analogy treatment.
 and
and  should satisfy the restriction (21). This subsequently gives us the following bounded values of velocities for traveling solutions.
should satisfy the restriction (21). This subsequently gives us the following bounded values of velocities for traveling solutions.
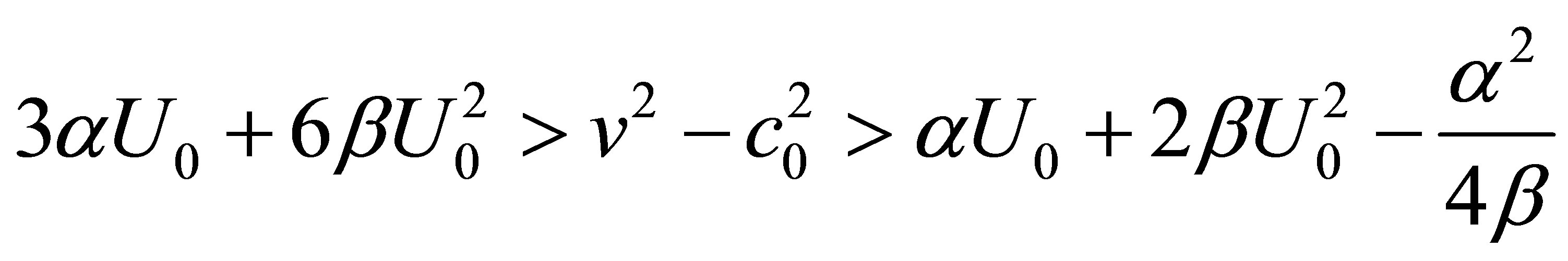 (23)
(23)
Let us transform a little the equation (22) for visualizing two types of solution; indeed, we can obtain the pedestal and bubble type soliton solutions. The pedestal type of solution could be visualized easily taking the formula (22) for available parameters. In contrast, in order to have a picture of bubble soliton we slightly transform the equation (22). By considering those requirements on nonnegative values of  for avoiding singularities we put
for avoiding singularities we put  and using the independent variable as
and using the independent variable as 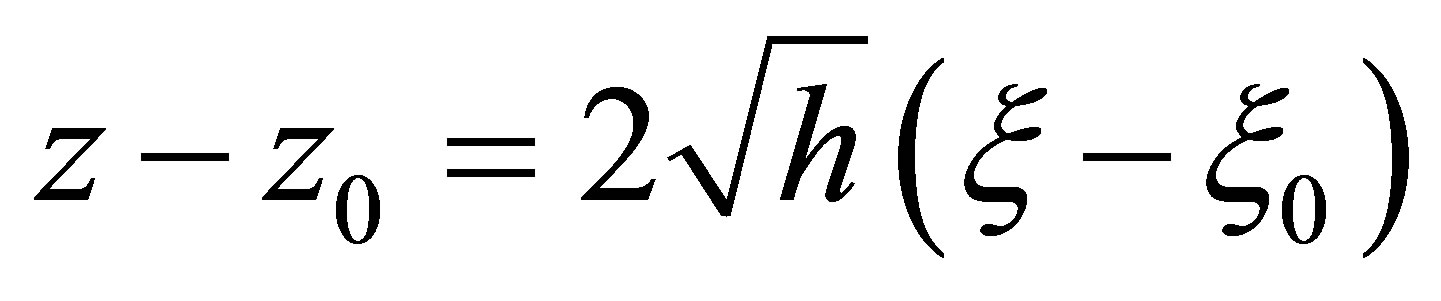 one can obtain the next representation of the solution
one can obtain the next representation of the solution
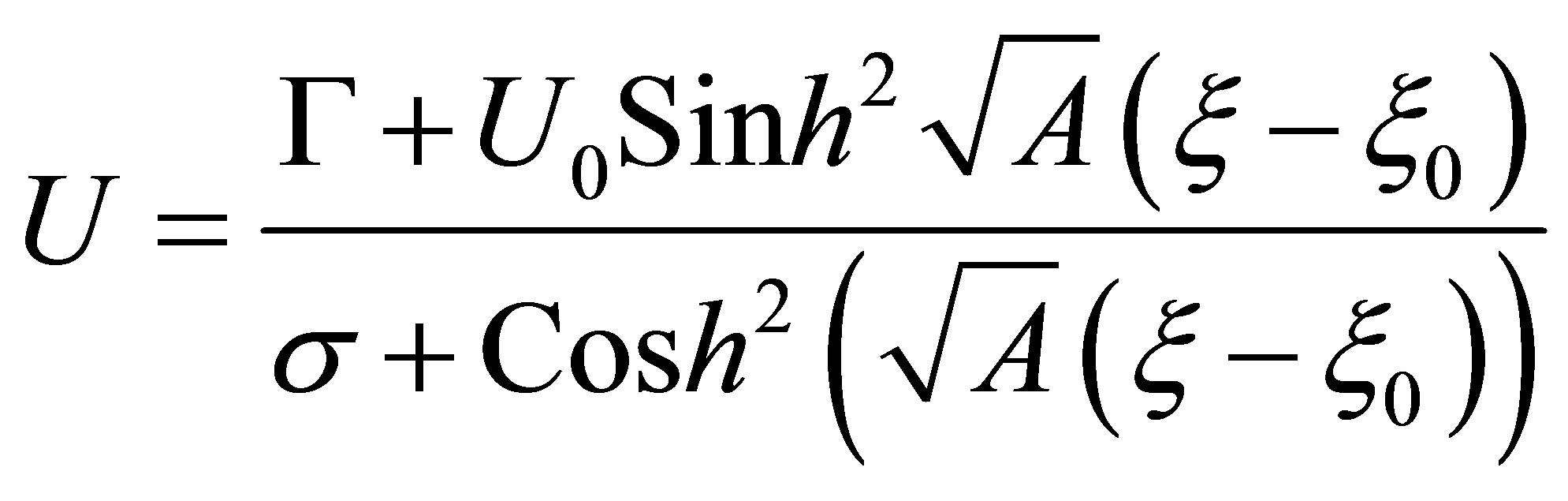 (24)
(24)
provided that
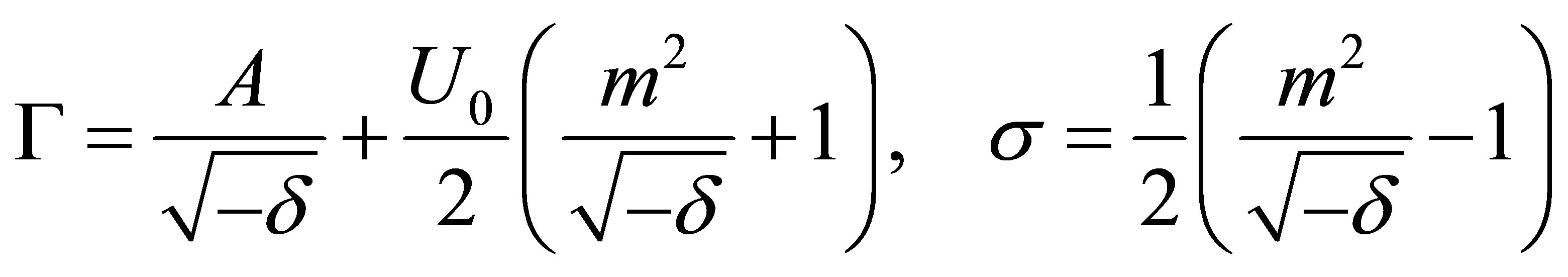 (25)
(25)
The “bright” soliton on condensate (pedestal) could be represented as Figure 1. This solution is a soliton-like excitation on the background of a constant value of condensed matter. It should be considered as a dual solution to the bubble solitons. Thus, bubble like solutions can also be obtained in the case when the velocities satisfy: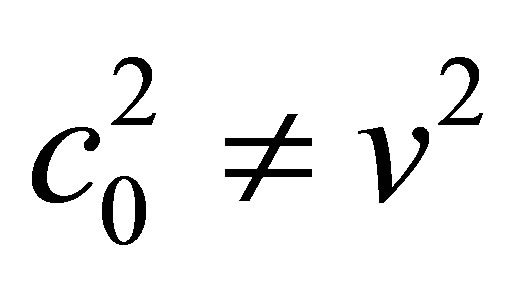 . These solitons on the condensate can be easily visualized by choosing appropriated values of the parameters. The simplest ones could be generated when the relation
. These solitons on the condensate can be easily visualized by choosing appropriated values of the parameters. The simplest ones could be generated when the relation 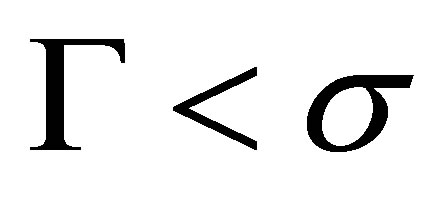 in Equation (25) holds for determined parametric values.
in Equation (25) holds for determined parametric values.
These two types of solutions (bubble and pedestal solutions) can exist inside the nerve dynamics. As we can

Figure 2. By using the following parameter values: 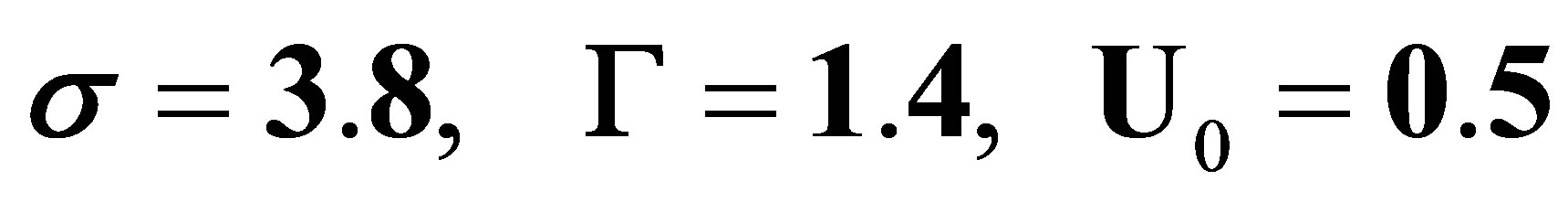 and making some reparameterization of variables in equation (24) one can depict the bubble like soliton as a dip on the background. This solution is also known as gray or dark solitons.
and making some reparameterization of variables in equation (24) one can depict the bubble like soliton as a dip on the background. This solution is also known as gray or dark solitons.
see the solutions that represent the local change of density lay above some baseline. In these two cases we have considered the neuron as an infinite entity in such a way that the mean density is the baseline that could be different from zero. So, we have a plateau with constant amplitude and along this plateau, the bubble or in some sense the small dip or rarefaction of density and the soliton on the condensate are propagating with some velocity whose values are restricted by the Equation (23). Along with the existence of bubble type of solitons, the soliton on the background also appears that should be dual to the first one. These local changes of density live on top of the nonvanishing background.
5. Dispersion Relation for Linear Waves
The normal mode perturbation with a frequency of  and wave number
and wave number  are taken proportional to
are taken proportional to
 (26)
(26)
For the linear variant of the Equation (4) the frequency is subjected to the dispersion relation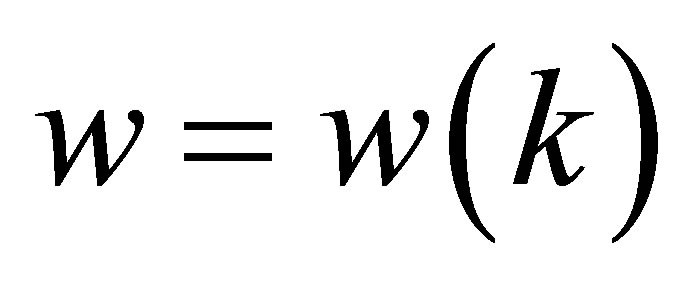 . Let us calculate the dispersion of small oscillation in vacuum
. Let us calculate the dispersion of small oscillation in vacuum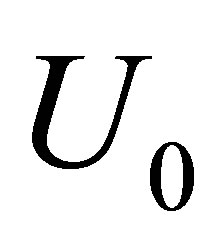 . For this we use the next representation of the solution
. For this we use the next representation of the solution
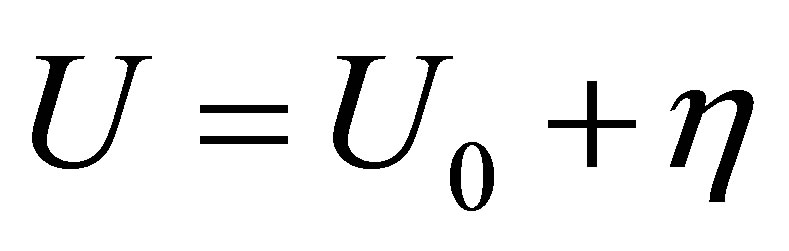 (27)
(27)
The linear equation takes the form
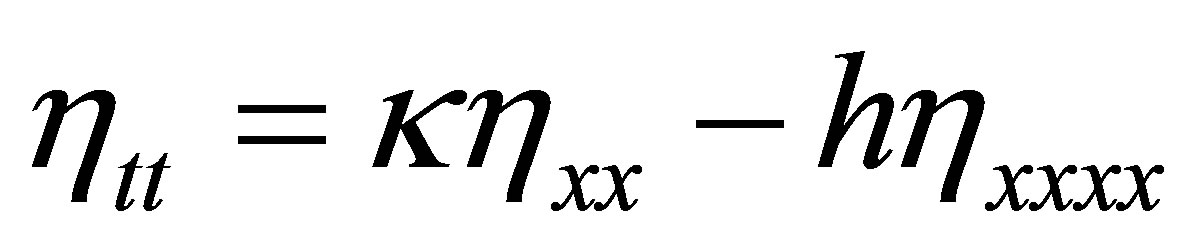 (28)
(28)
with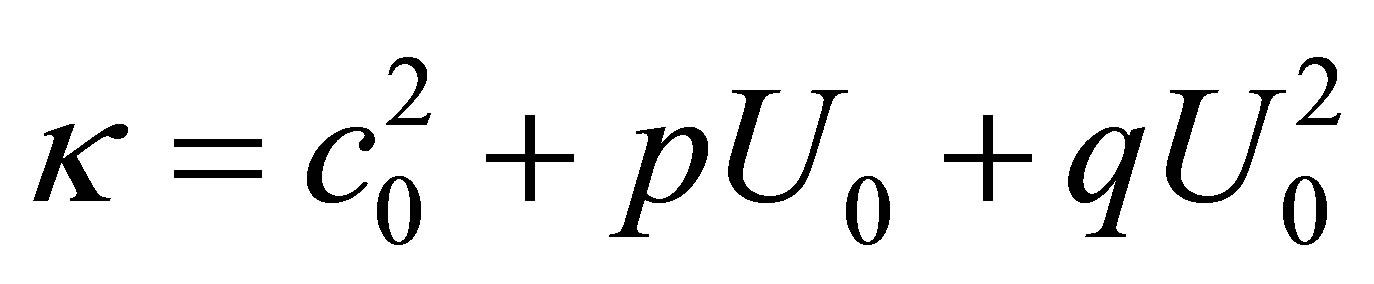 . As it is well known the dispersion relation can be obtained from (28) as
. As it is well known the dispersion relation can be obtained from (28) as
 (29)
(29)
From the last equation we see that the considered condensate is linearly stable when 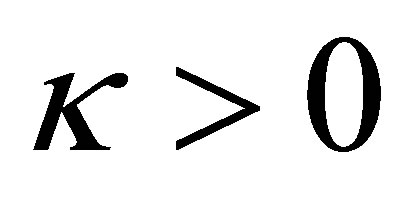 provided that
provided that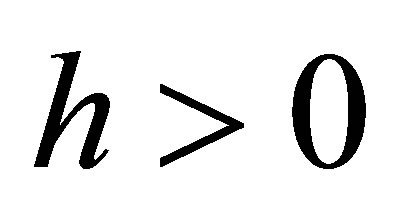 . In this sense our solutions are constructed above some stable vacuum state and are physically accepted. When
. In this sense our solutions are constructed above some stable vacuum state and are physically accepted. When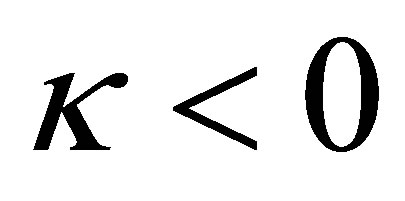 , we observe some restriction for the wave number that limits the linear stability of the background. These important new properties along with the important issue of this investigation concerning the stability of these solutions should be reported elsewhere.
, we observe some restriction for the wave number that limits the linear stability of the background. These important new properties along with the important issue of this investigation concerning the stability of these solutions should be reported elsewhere.
6. Conclusions
We have discussed in this contribution the appearance of bubbles and solitons on the background along the axon, based on the model reported in the pioneering work of [9]. These solutions propagate over the spatially homogeneous background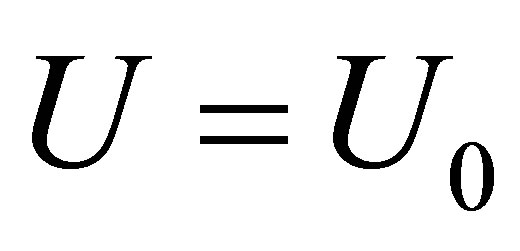 . The potential piece for the solution is represented in Figure 3.
. The potential piece for the solution is represented in Figure 3.
As we can see from (Figure 3) the vacuum of emergence of bubbles and pedestal soliton solutions is a relative minimum of the potential. In some sense they seem
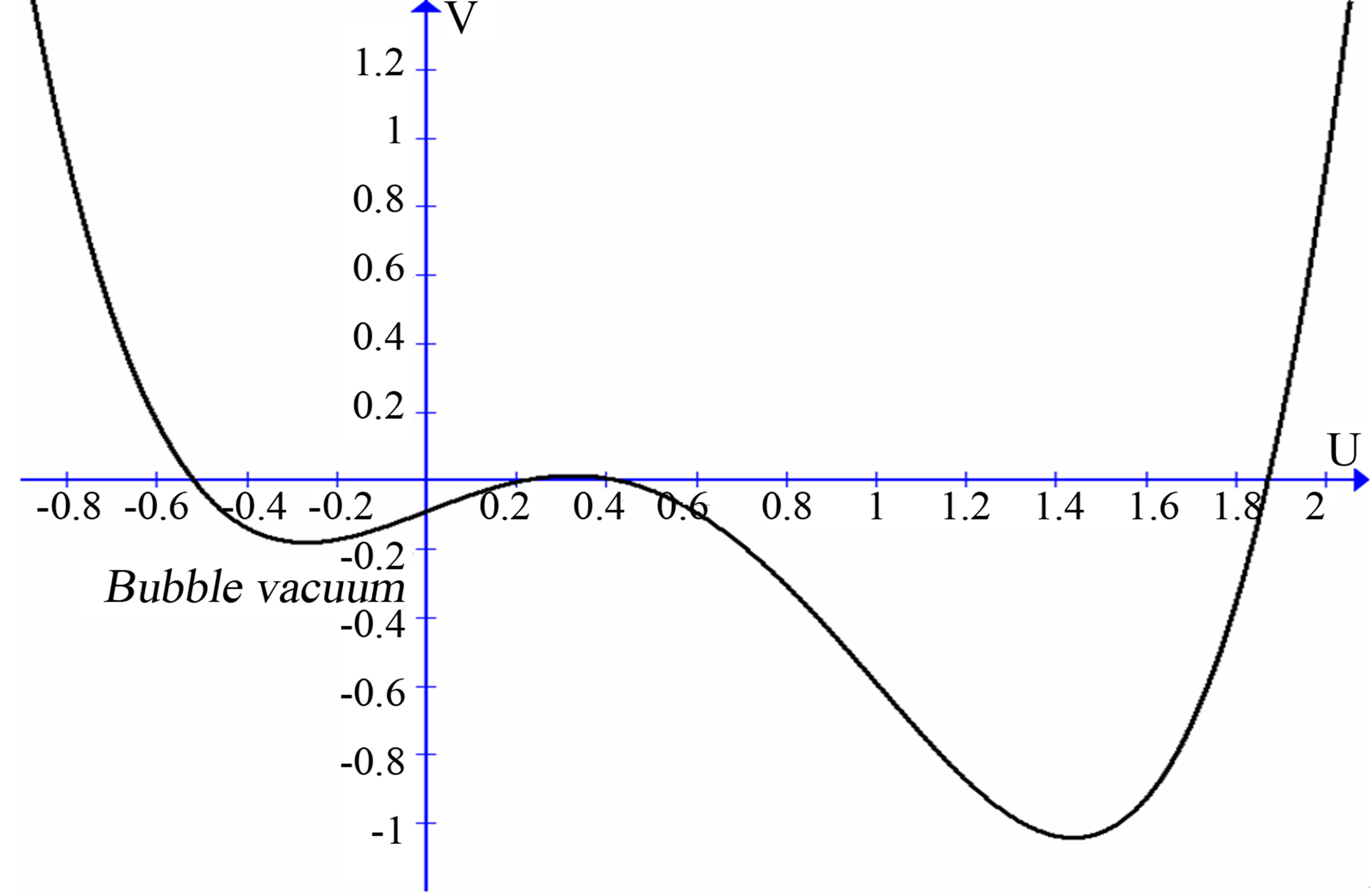
Figure 3. The existence of bubbles or gray and pedestal solitons is due to the manifestation of relative minimum, the “false vacuum” of the potential piece of its energy V(U) from Equation (4).
to be dual solutions. The traveling small dip or rarefaction and soliton excitation on the background can exist and can run with constant velocity along the nerve. Thus, the long pulse plateau in the nerve could be perturbed by bubble and bright solitons on the background. Therefore, in both directions of the axis, for say , at long distances from the active zone, the density displacements will maintain their value, forming the nonvanishing boundary condition. By taking into consideration this physical reason and by integrating the nonlinear equation proposed in the work (2), for specific parameter regions, we have found solutions that move with the same velocity of sound i.e. sonic, sub and super sonic bubble and solitons on background.
, at long distances from the active zone, the density displacements will maintain their value, forming the nonvanishing boundary condition. By taking into consideration this physical reason and by integrating the nonlinear equation proposed in the work (2), for specific parameter regions, we have found solutions that move with the same velocity of sound i.e. sonic, sub and super sonic bubble and solitons on background.
These solutions could eventually be responsible for various fundamental processes inside the nerve, especially those processes that involve some kind of parametric phase transitions. This is because of the realistic interpretation of bubbles as a nucleus of some stable phases in the bubble vacuum or a metastable one. Also, both solutions, that is, the bubble and the soliton on the background obtained here as particular soliton-like solutions for specific values of parameters, could be used by the nerve system for enhancing confidentiality in communication tasks. For instance, as the bubble soliton amplitude vanishes or minimizes during propagation along the nerve, this wave could be used to perform communication transmission for security, whereas the required information can be retrieved by the dark/bright soliton conversion on the background. Apparently as has been mentioned above, these solutions could conform some informational code structures for preserving and transmitting valid information along the nerve.
7. Acknowledgements
Authors are indebted to Professor V.G. Makhankov for constant support and discussions. We acknowledge the efforts of SIEA-UAEMEX for supporting the fundamental research and also the financial aid of Secretaria de Educacion Publica de Mexico (SEP) under the project FEO1/2012 103.5/12/2126 for scientific groups.
REFERENCES
- A. L. Hodgkin and A. F. Huxley, “A Quantitative Description of Membrane Current and Its Application to Conduction and Excitation in Nerve,” The Journal of Physiology, Vol. 117, No. 4, 1952, pp. 500-544.
- B. Katz, “Nerve, Muscle, and Synapse,” McGraw-Hill, New York, 1966.
- R. FitzHugh, “Impulses and Physiological States in Theoretical Models,” Biophysical Journal, Vol. 1, No. 6, 1961 pp. 445-466. http://dx. http://dx.doi.org/10.1016/S0006-3495(61)86902-6
- J. Nagumo, S. Arimoto and S. Yoshizawa, “An Active Pulse Transmission Line Simulating Nerve Axon,” Proceedings of the IRE, Vol. 50, No. 10, 1962, pp. 2061- 2070. http://dx.doi.org/10.1109/JRPROC.1962.288235
- S. Abbasbandy, “Soliton Solutions for the Fitzhugh-Nagumo Equation with the Homotopy Analysis Method,” Applied Mathematical Modelling, Vo. 32, No. 12, 2008, pp. 2706-2714. http://dx.doi.org/10.1016/j.apm.2007.09.019
- F. Ongay and M. Aguero, “Bifurcations in the Fitzhugh— Nagumo System,” Ciencia Ergo Sum, Vol. 17, No. 3, 2011, pp. 295-306.
- Y. Kobatake, I. Tasaki and A. Watanabe, “Phase Transition in Membrane with Reference to Nerve Excitation,” Advances in Biophysics, Vol. 2, 1971, pp. 1-31
- T. Heinburg and A. Jackson, “On Soliton Propagation in Biomembranes and Nerves,” Proceedings of the National Academy of Sciences, Vol. 102, No. 28, 2005, pp. 9790- 9795. http://dx.doi.org/10.1073/pnas.0503823102
- B. Lautrup, R. Appali, A. D. Jackson and T. Heimburg, “The Stability of Solitons in Biomembranes and Nerves,” The European Physical Journal E, Vol. 34, 201, p. 57. http://dx.doi.org/10.1140/epje/i2011-11057-0
- E. Villagran, A. Ludu, R. Hustert, P. Gumrich, A. D. Jackson and T. Heimburg, “Periodic Solutions and Refractory Periods in the Soliton Theory for Nerves He Locust Femoral Nerve,” Biophysical Chemistry, Vol. 153, No. 2-3, 2011, pp. 159-167. http://dx.doi.org/10.1016/B978-0-12-396534-9.00009-X
- R. Appali, S. Petersen and U. van Rienen, “A Comparison of Hodgkin-Huxley and Soliton Neural Theories,” Advances in Radio Science, Vol. 8, 2010, pp. 75-79. http://dx.doi.org/10.5194/ars-8-75-2010
- V. G. Makhankov, “Soliton Phenomenology,” Kluwer Academic Publishers, Norwell, 1990. dhttp://dx.doi.org/10.1007/978-94-009-2217-4
- N. N. Akhmediev and A. Ankevich, “Solitons, Nonlinear Pulses and Beams,” Chapman and Hall, London, 1997.
- D. E. Pelinovsky and P. G. Kevrekidis, “Dark Solitons in External Potentials,” Zeitschrift für angewandte Mathematik und Physik, Vol. 59, No. 4, 2008, pp. 559-599. http://dx.doi.org/10.1007/s00033-007-6120-0
- V. N. Serkin, A. Hasegawa, “Novel Soliton Solutions of the Nonlinear Schrodinger Equation Model,” Physical Review Letters, Vol. 85, No. 21, 2000, pp. 4502-4505. http://dx.doi.org/10.1103/PhysRevLett.85.4502
- S. Rajendran, P. Muruganandam and M. Lakshmanan, “Bright and Dark Solitons in a Quasi 1D Bose-Einstein Condensates Modelled by 1D Gross-Pitaevskii Equation with Time-Dependent Parameters,” Physica D, Vol. 239, No. 7, 2010, pp. 366-386. http://dx.doi.org/10.1016/j.physd.2009.12.005
- Yu. Kivshar and B. Luther-Davies, “Dark Optical Solitons: Physics and Applications,” Physics Reports, Vol. 298, No. 2-3, 1998, p. 81. http://dx.doi.org/10.1016/S0370-1573(97)00073-2
- D. J. Frantzeskakis, “Dark Solitons in Atomic Bose-Einstein Condensates: From Theory to Experiments,” Journal of Physics A: Mathematical and Theoretical, Vol. 43, No. 21, 2010, Article ID: 21300. http://dx.doi.org/10.1088/1751-8113/43/21/213001

