International Journal of Modern Nonlinear Theory and Application
Vol.2 No.1A(2013), Article ID:29401,5 pages DOI:10.4236/ijmnta.2013.21A008
Transitivity and Chaoticity in 1-D Cellular Automata
1School of Science, Hangzhou Dianzi University, Hangzhou, China
2Department of Electronic Engineering, City University of Hong Kong, Hong Kong, China
3College of Pharmaceutical Sciences, Zhejiang Chinese Medical University, Hangzhou, China
Email: fychen@hdu.edu.cn, eegchen@cityu.edu.hk, jin.weifeng@hotmail.com
Received November 22, 2012; revised December 30, 2012; accepted January 14, 2013
Keywords: Bernoulli Subshift of Finite Type; Cellular Automata; Devaney Chaos; Symbolic Dynamics; Topological Transitivity
ABSTRACT
Recent progress in symbolic dynamics of cellular automata (CA) shows that many CA exhibit rich and complicated Bernoulli-shift properties, such as positive topological entropy, topological transitivity and even mixing. Noticeably, some CA are only transitive, but not mixing on their subsystems. Yet, for one-dimensional CA, this paper proves that not only the shift transitivity guarantees the CA transitivity but also the CA with transitive non-trivial Bernoulli subshift of finite type have dense periodic points. It is concluded that, for one-dimensional CA, the transitivity implies chaos in the sense of Devaney on the non-trivial Bernoulli subshift of finite types.
1. Introduction
1.1. Cellular Automata
Cellular automata (CA), formally introduced by von Neumann in the late 1940s and early 1950s, are a class of spatially and temporally discrete deterministic systems, characterized by local interactions and an inherently parallel form of evolution [1]. In the late 1960s, Conway proposed his now-famous Game of Life, which shows the great potential of CA in simulating complex systems [2]. In the 1980s, Wolfram focused on the analysis of dynamical systems and studied CA in detail [3,4]. In 2002, he introduced the monumental work A New Kind of Science [5]. In fact, mathematical theory of CA was firstly developed by Hedlund about two decades after Neumann’s seminal work [6]. Since 2002, Chua et al. provided a rigorous nonlinear dynamical approach to Wolfram’s empirical observations [7-10]. All elementary CA (ECA) rules are reorganized into four groups in terms of finite bit stings. There are 40 topologically-distinct period- rules
rules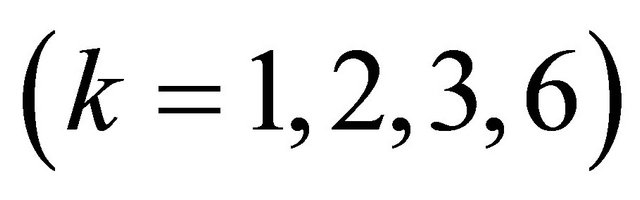 , 30 topologically-distinct Bernoulli shift rules, 10 complex Bernoulli shift rules, and 8 hyper Bernoulli shift rules. Recently, the dynamical properties of Chua’s periodic rules and robust Bernoulli-shift rules with distinct parameters have been investigated from the viewpoint of symbolic dynamics [11-17].
, 30 topologically-distinct Bernoulli shift rules, 10 complex Bernoulli shift rules, and 8 hyper Bernoulli shift rules. Recently, the dynamical properties of Chua’s periodic rules and robust Bernoulli-shift rules with distinct parameters have been investigated from the viewpoint of symbolic dynamics [11-17].
By a theorem of Hedlund [6], a map  is an one-dimensional cellular automata (1-D CA) if and only if it is continuous and commutes with the shift map
is an one-dimensional cellular automata (1-D CA) if and only if it is continuous and commutes with the shift map![]() . For any 1-D CA, there exists a radius
. For any 1-D CA, there exists a radius 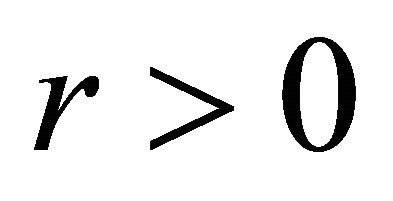 and a local map
and a local map  such that
such that
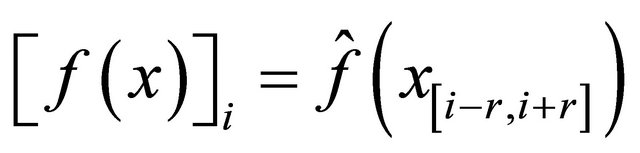 where notetions will be precisely defined below. In particular,
where notetions will be precisely defined below. In particular,  is an ECA global map when
is an ECA global map when  and
and 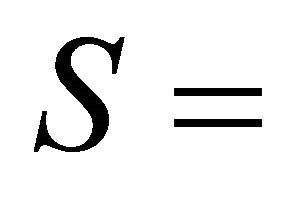
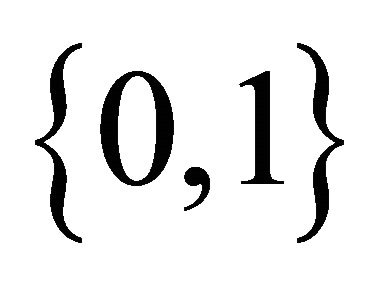 . Each ECA can be expressed by a 3-bit Boolean function and coded by an integer
. Each ECA can be expressed by a 3-bit Boolean function and coded by an integer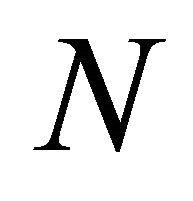 , which is the decimal notation of the output binary sequence of the Boolean function [5,7,18].
, which is the decimal notation of the output binary sequence of the Boolean function [5,7,18].
1.2. Definition of Chaos
Let 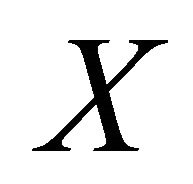 be a metric space and
be a metric space and :
:  be a continuous map.
be a continuous map.  is said to be topologically transitive or simply transitive if, for any non-empty open subsets
is said to be topologically transitive or simply transitive if, for any non-empty open subsets 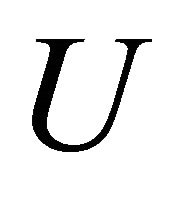 and
and 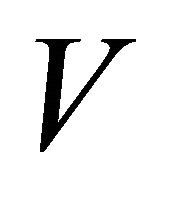 of
of  there exists a natural number
there exists a natural number ![]() such that
such that ;
;  is topologically mixing or simply mixing if there exists a natural number
is topologically mixing or simply mixing if there exists a natural number  such that
such that  for all
for all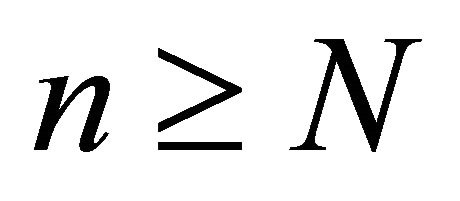 ;
;  is sensitive to initial conditions (or simply sensitive) if there exists a
is sensitive to initial conditions (or simply sensitive) if there exists a 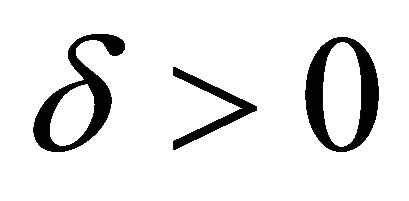 such that, for
such that, for  and for any neighborhood
and for any neighborhood 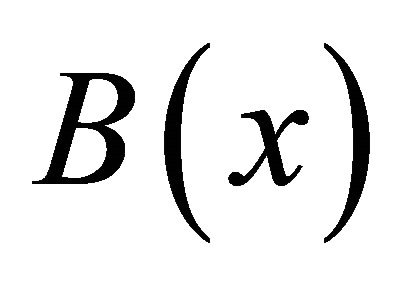 of
of![]() , there exists a
, there exists a  and a natural number
and a natural number ![]() such that
such that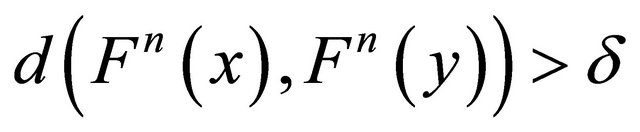 , where
, where ![]() is a distance defined on
is a distance defined on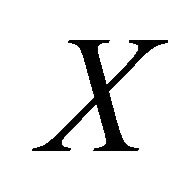 .
.
Let 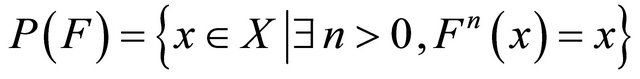 be the set of periodic points of
be the set of periodic points of .
. 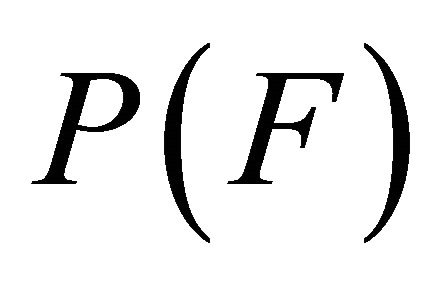 is said to be a dense subset of
is said to be a dense subset of 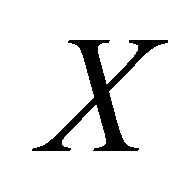 if, for any
if, for any  and any constant
and any constant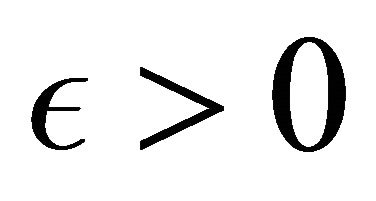 , there exists a
, there exists a  such that
such that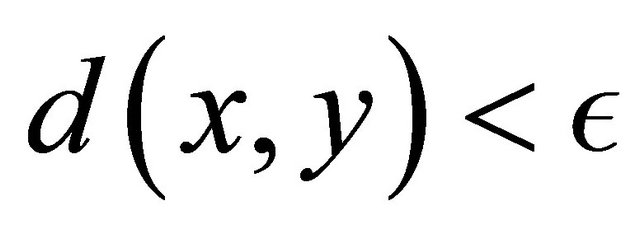 .
.
Definition 1.  is chaotic on
is chaotic on 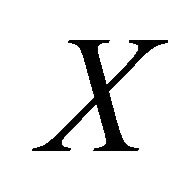 in the sense of Devaney if (1)
in the sense of Devaney if (1) is transitive, (2)
is transitive, (2) 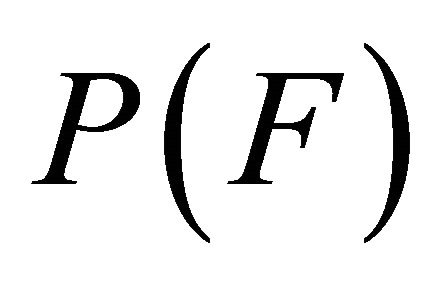 is a dense subset of
is a dense subset of , (3)
, (3) is sensitive [19].
is sensitive [19].
It has been proved that additive 1-D CA are chaotic [20]. For general dynamical systems, it has been proved that (1) and (2) together imply (3) [21], and for 1-D CA, (1) implies (3) [22]. In the next section of this paper, it will be proved that, for 1-D CA with Bernoulli subshift of finite type (BSFT), (1) also implies (2).
1.3. Symbolic Dynamical Systems and SFT
For a finite alphabet , a word over
, a word over ![]() is a finite sequence
is a finite sequence  of elements of
of elements of![]() . Denote by
. Denote by  the set of all words of length
the set of all words of length![]() . If
. If ![]() is a finite or infinite word and
is a finite or infinite word and  is an interval of integers on which
is an interval of integers on which ![]() is defined, then denote
is defined, then denote
![]() . Moreover,
. Moreover, ![]() is said to be a subword of
is said to be a subword of![]() , denoted as
, denoted as , if
, if 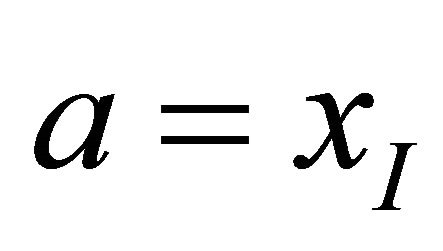 for some interval
for some interval , where
, where 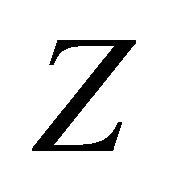 is the set of all integers. The set of bi-infinite configurations is denoted by
is the set of all integers. The set of bi-infinite configurations is denoted by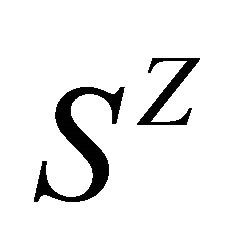 , and a distance
, and a distance ![]() on
on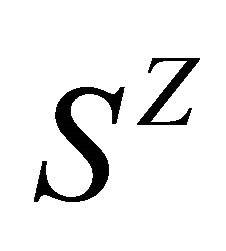 is defined by
is defined by
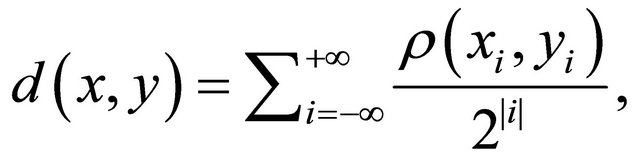
where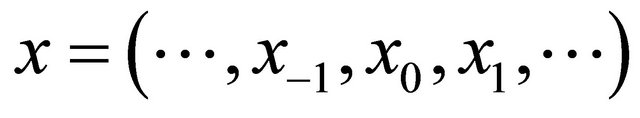 ,
,
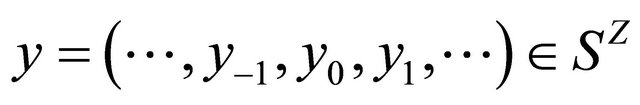 , and
, and 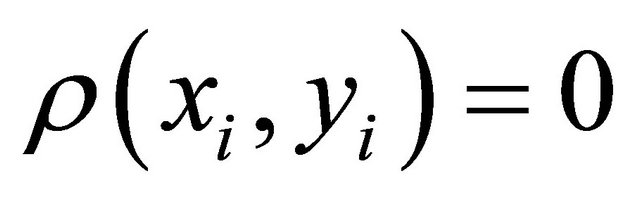 if
if  , or
, or  otherwise. It is known that
otherwise. It is known that 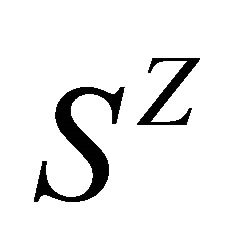 is a compact, perfect and totally disconnected metric space [23].
is a compact, perfect and totally disconnected metric space [23].
For a map , a set
, a set 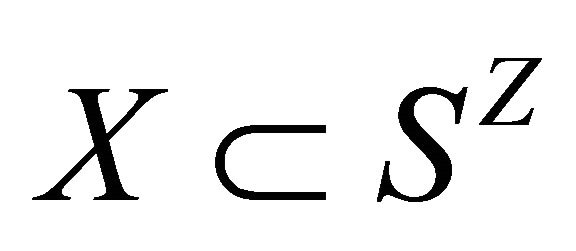 is said to be
is said to be  if
if . If
. If  is closed and
is closed and
 then
then 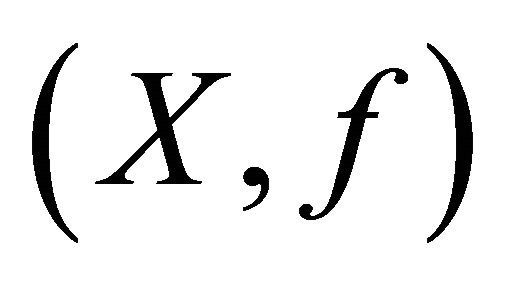 is called a subsystem of the dynamical system
is called a subsystem of the dynamical system . For example, let
. For example, let  be a set of some words of length
be a set of some words of length ![]() over
over![]() , and
, and  be the set of the bi-infinite configurations consisting of all the words in
be the set of the bi-infinite configurations consisting of all the words in . Then,
. Then, 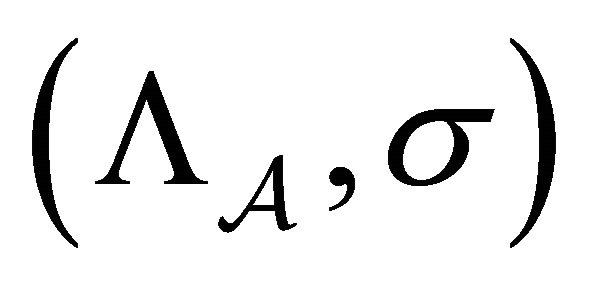 is a subsystem of
is a subsystem of
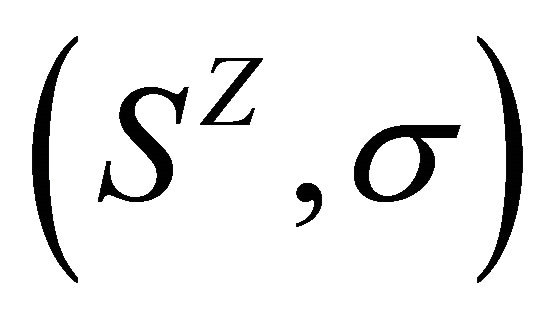 , where
, where ![]() is the left shift
is the left shift 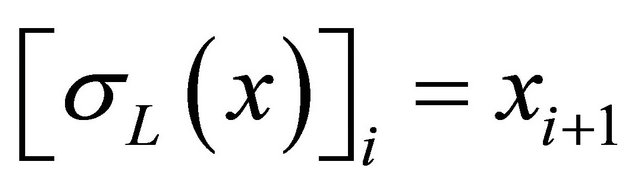 (or the right shift
(or the right shift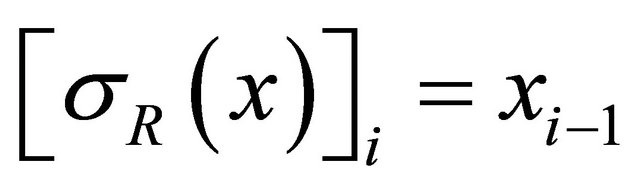 ) defined on
) defined on , and
, and  is called the determinative block system of
is called the determinative block system of . The subsystem
. The subsystem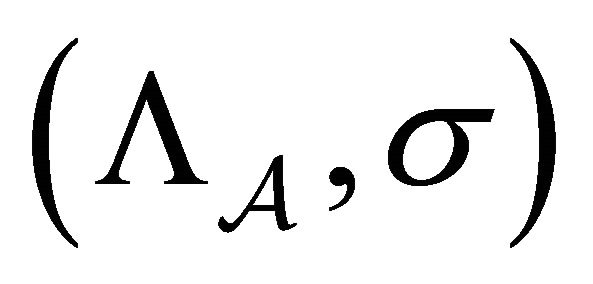 , or simply
, or simply ![]() is called a subshift of finite type (SFT) with respect to
is called a subshift of finite type (SFT) with respect to .
.
Furthermore,  can be described by a finite directed graph,
can be described by a finite directed graph, 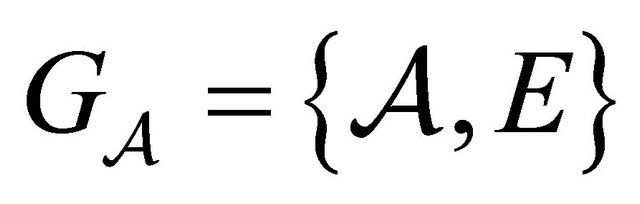 , where each vertex is labeled by a word in
, where each vertex is labeled by a word in , and
, and  is the set of edges connecting the vertices in
is the set of edges connecting the vertices in . Two vertices
. Two vertices 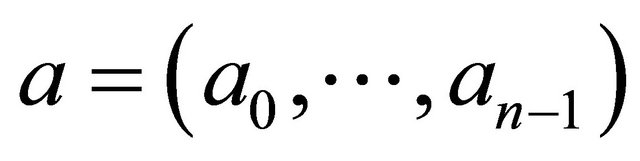 and
and 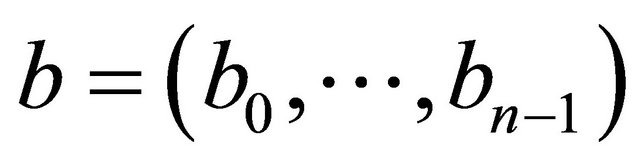 are connected by an edge
are connected by an edge 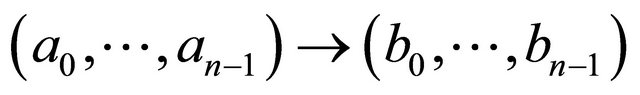 if and only if
if and only if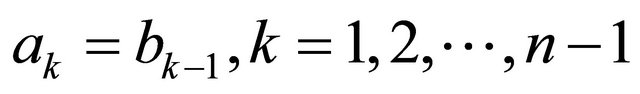 . One can think of each element of
. One can think of each element of  as a bi-infinite path on the graph
as a bi-infinite path on the graph . Whereas a directed graph corresponds to a square transition matrix
. Whereas a directed graph corresponds to a square transition matrix ![]() with
with 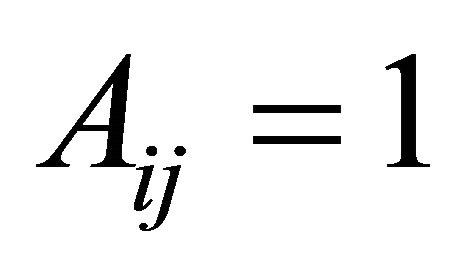 if and only if there is an edge from vertex
if and only if there is an edge from vertex 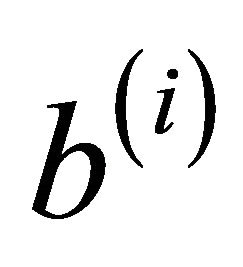 to vertex
to vertex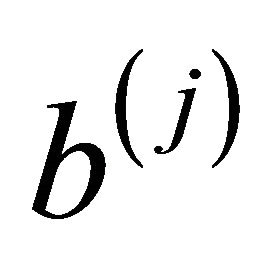 , where
, where  is the number of elements in
is the number of elements in , and
, and  (or
(or ) is the code of the corresponding vertex in
) is the code of the corresponding vertex in ,
, . Thus,
. Thus, 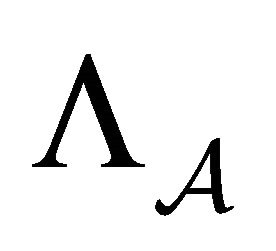 is precisely defined by the transition matrix
is precisely defined by the transition matrix .
.
Remarkably, a 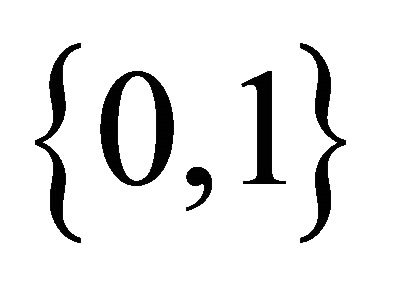 square matrix
square matrix  is irreducible if, for any
is irreducible if, for any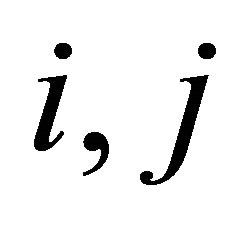 , there exists an
, there exists an ![]() such that
such that ; aperiodic if there exists an
; aperiodic if there exists an ![]() such that
such that  for all
for all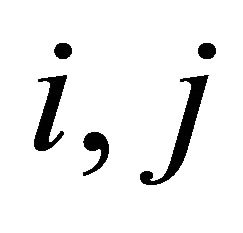 , where
, where 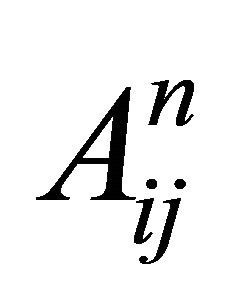 is the
is the  entry of the power matrix
entry of the power matrix
 . If
. If  is an SFT of
is an SFT of , then it is transitive if and only if
, then it is transitive if and only if  is irreducible; it is mixing if and only if
is irreducible; it is mixing if and only if  is aperiodic. Equivalently,
is aperiodic. Equivalently,  is irreducible if and only if for every ordered pair of vertices
is irreducible if and only if for every ordered pair of vertices  and
and  there is a path in
there is a path in 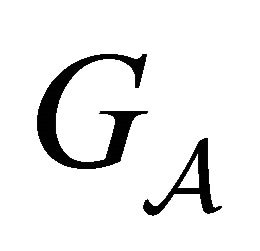 starting at
starting at 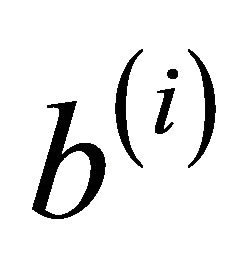 and ending at
and ending at 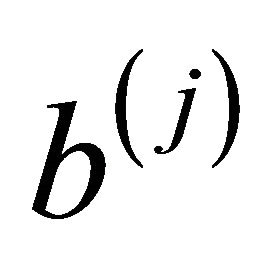 [23,24].
[23,24].
2. Transitivity and Chaoticity
In this section, it is proved that, for any 1-D CA restricted on its Bernoulli-shift subsystem, the shift transitivity implies the CA transitivity, and transitive nontrivial Bernoulli subshift of finite type (BSFT) has dense periodic points. Consequently, for 1-D CA, transitivity implies chaos in the sense of Devaney on the non-trivial BSFT.
2.1. Shift Transitivity Implies CA Transitivity
Definition 2. A closed invariant subset 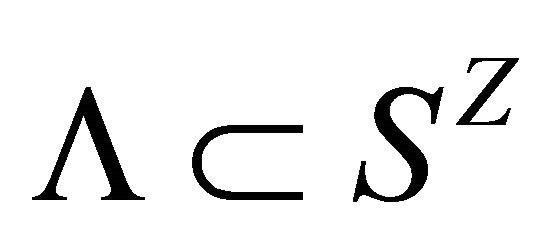 of a 1-D CA
of a 1-D CA  is called a Bernoulli-shift subsystem if there exists an integer pair
is called a Bernoulli-shift subsystem if there exists an integer pair 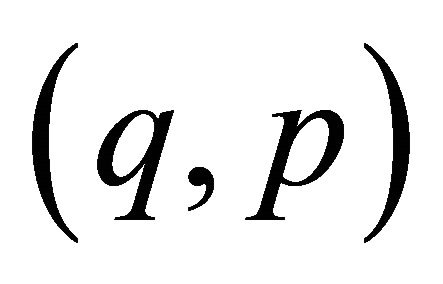 with
with  such that
such that , where
, where  is the radius of the local map
is the radius of the local map 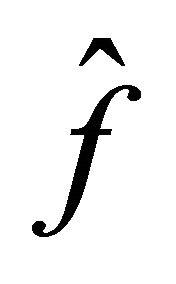 of the CA
of the CA  and
and ![]() is the left (or right) shift map.
is the left (or right) shift map.
For simplicity, only consider ![]() as the left shift in the following discussion.
as the left shift in the following discussion.
Proposition 1. If  is a Bernoulli-shift subsystem of a 1-D CA
is a Bernoulli-shift subsystem of a 1-D CA 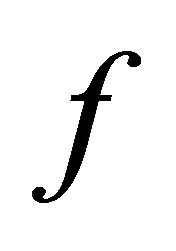 with
with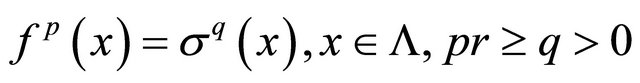 then there exists a
then there exists a  -sequence set
-sequence set  such that
such that
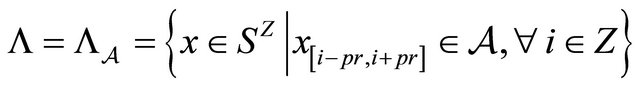 .
.
Proof: If  is the local map of
is the local map of , then one can get the
, then one can get the ![]() times iteration of
times iteration of 
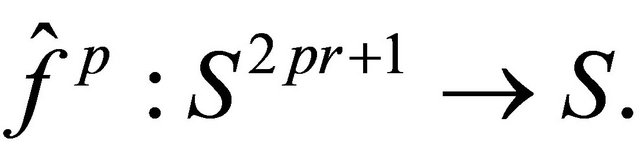 Thus,
Thus, 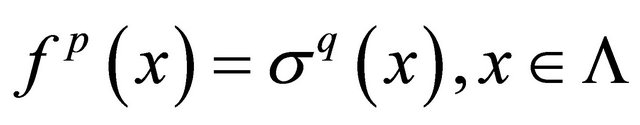 , if and only if
, if and only if
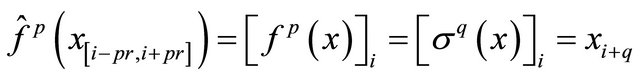 for all
for all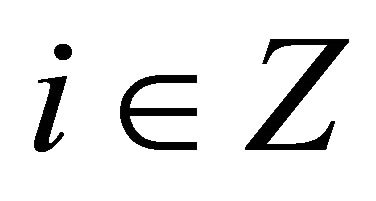 . Let
. Let
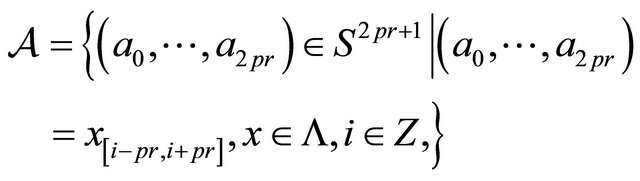
and
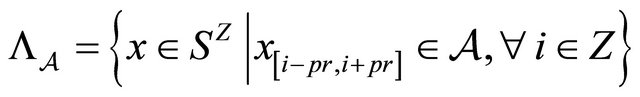 where
where  is a finite set since
is a finite set since 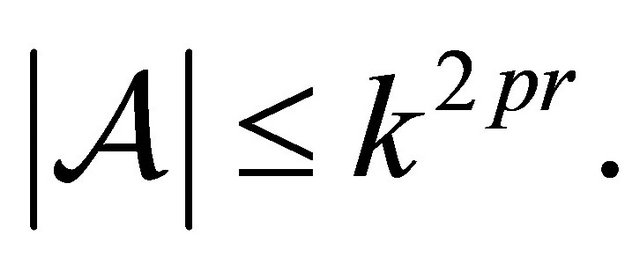 Then, it follows that
Then, it follows that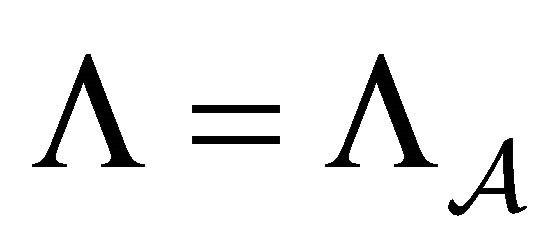 .
.
Definition 3. The Bernoulli-shift subsystem 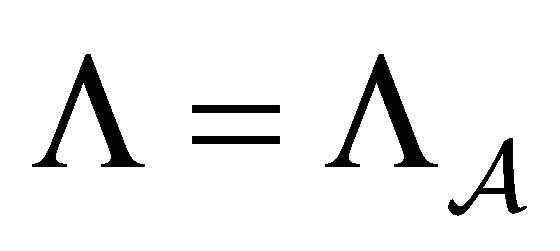 in Proposition 1 is called the Bernoulli subshift of finite type (BSFT), and
in Proposition 1 is called the Bernoulli subshift of finite type (BSFT), and  is called the determinative block system of
is called the determinative block system of . If BSFT is an infinite set, then it is said to be non-trivial.
. If BSFT is an infinite set, then it is said to be non-trivial.
Based on Definitions 1, 3 and Proposition 1, an obvious result is the following proposition.
Proposition 2. Consider two BSFTs,  and
and , of a 1-D CA
, of a 1-D CA  with
with
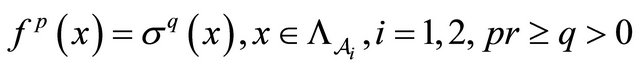 .
.
Then,  if and only if
if and only if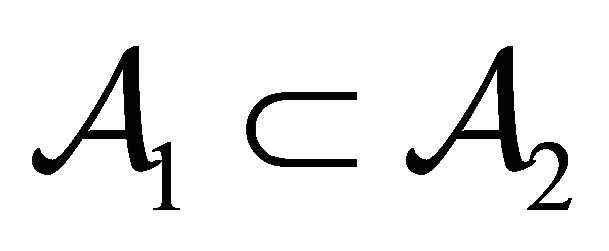 .
.
Theorem 1. Let  be a BSFT of a 1-D CA
be a BSFT of a 1-D CA 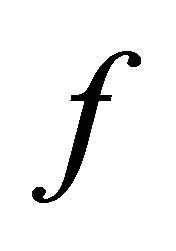 with
with 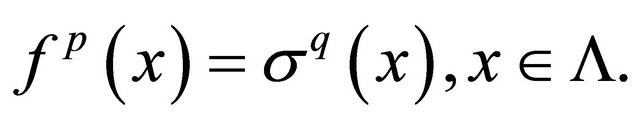 If the shift
If the shift 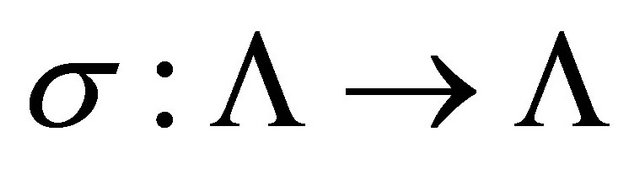 is transitive, then
is transitive, then  is also transitive.
is also transitive.
Proof: Since the transitivity of ![]() on
on  is equivalent to the existence of a
is equivalent to the existence of a 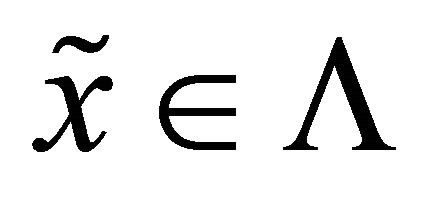 such that
such that
 where
where

is the orbit of ![]() starting from
starting from  and
and 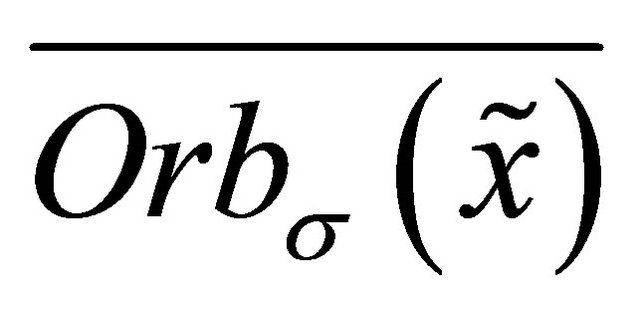 is its closure [14,15]. It can be verified that for any
is its closure [14,15]. It can be verified that for any 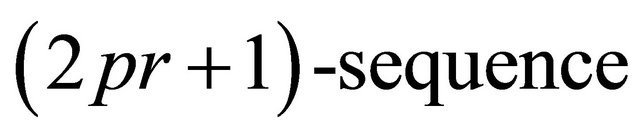
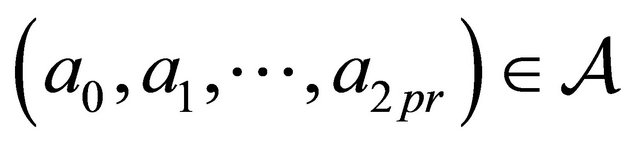 , there exists at least an
, there exists at least an  such that
such that
![]() .
.
Conversely, for any , the
, the 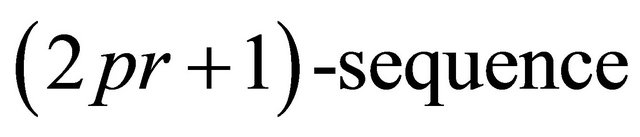
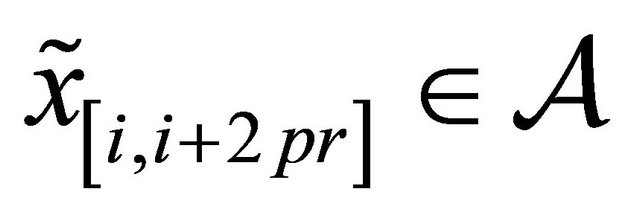 .
.
For the 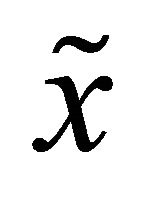 above, consider the orbit
above, consider the orbit
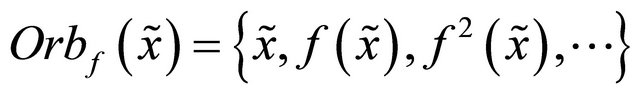
and let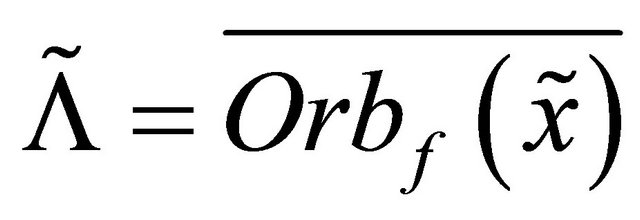 . It is clear that
. It is clear that  is closed and
is closed and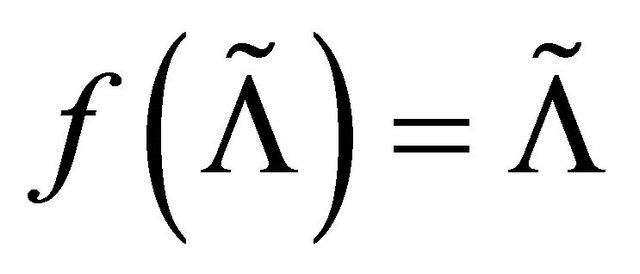 . Because
. Because  is
is 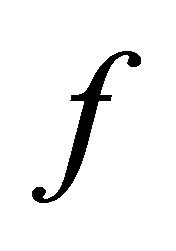 -invariant and closed, one has
-invariant and closed, one has 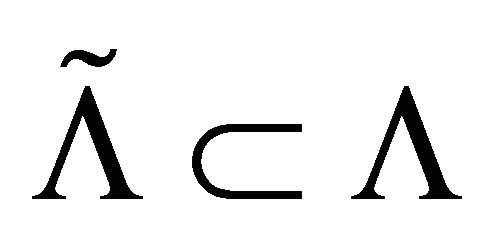 and
and . Obviously,
. Obviously, 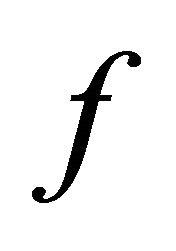
is transitive on .
.
Let  denote the determinative block system of
denote the determinative block system of . On one hand, based on Proposition 2 and
. On one hand, based on Proposition 2 and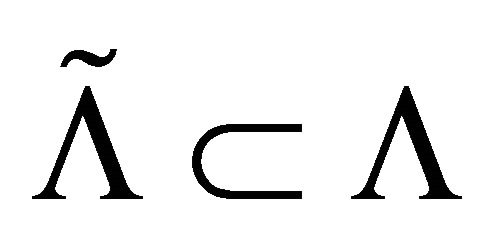 , one has
, one has . On the other hand, since
. On the other hand, since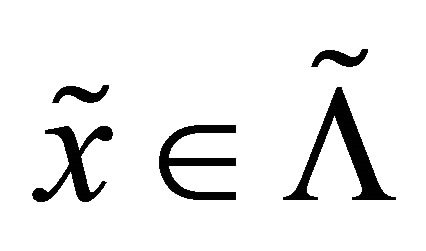 , it follows that
, it follows that![]() , but the
, but the 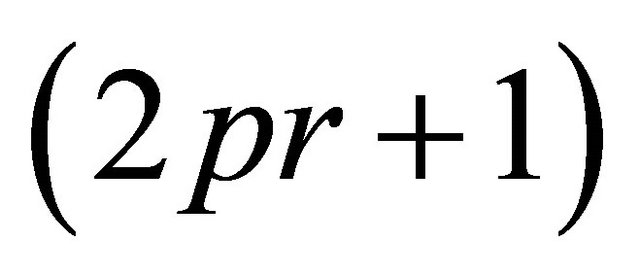 -sequence set consisting of
-sequence set consisting of 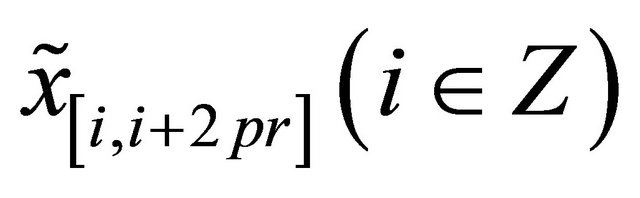 is
is . This implies
. This implies
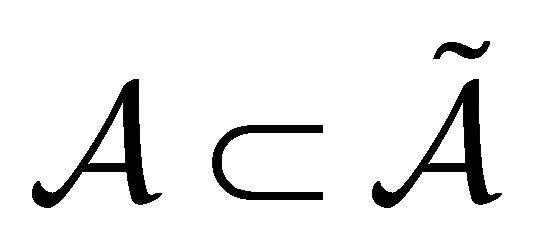 and
and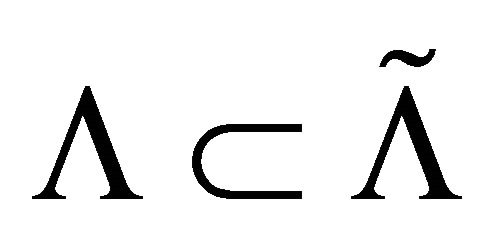 . Thus,
. Thus, 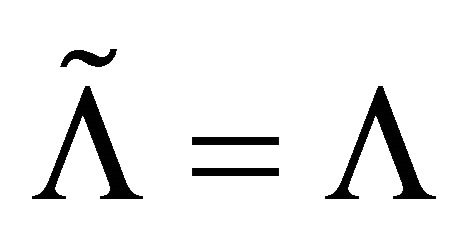 , i.e.,
, i.e.,  is transitive on
is transitive on .
.
Remark 1.
1) Theorem 1 gives a convenient method to check if a CA 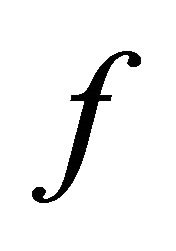 is transitive on a BSFT, since
is transitive on a BSFT, since ![]() is transitive on SFT if and only if the transition matrix corresponding to the SFT is irreducible [23,24].
is transitive on SFT if and only if the transition matrix corresponding to the SFT is irreducible [23,24].
2) Theorem 1 shows that the shift transitivity implies the CA transitivity on the BSFT, but the inverse implication may not be correct, with a counter example of ECA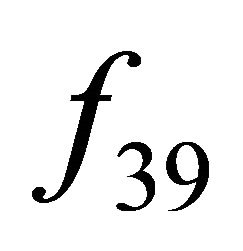 . One has
. One has , where
, where 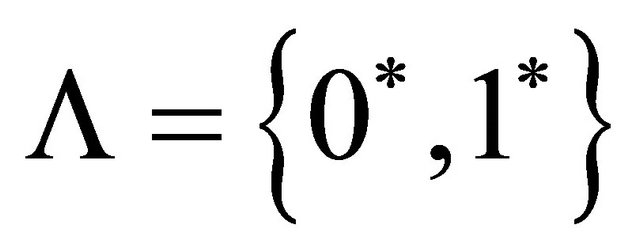
and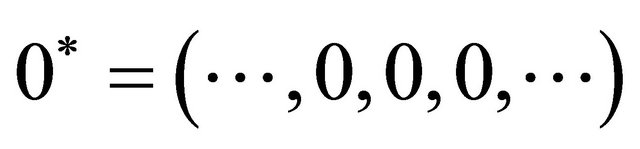 ,
,  , so
, so  contains two points. It is clear that
contains two points. It is clear that 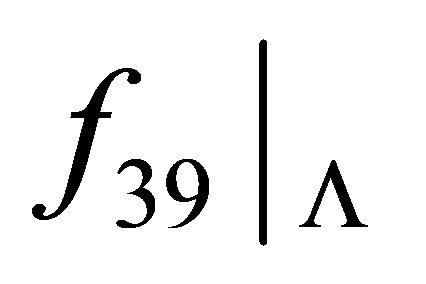 is transitive but
is transitive but ![]() is not. In case BSFT is an infinite set, whether the CA transitivity implies the shift transitivity on the BSFT is still an open problem.
is not. In case BSFT is an infinite set, whether the CA transitivity implies the shift transitivity on the BSFT is still an open problem.
3) When a BSFT  is a finite set on which
is a finite set on which 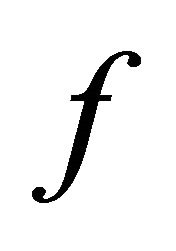 is transitive, then it is a set of
is transitive, then it is a set of  points,
points,  for some
for some 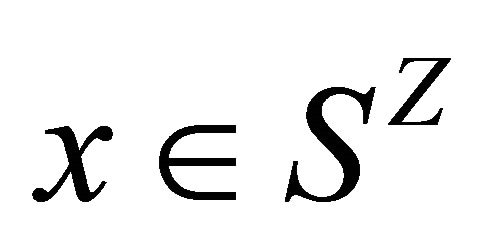 and
and  , it is said that
, it is said that  is trivial.
is trivial.
Remark 2.
Recall two claims proved in [22]: 1) transitive 1-D CA is always sensitive; 2) a 1-D CA  is transitive but not sensitive on a SFT
is transitive but not sensitive on a SFT  if and only if
if and only if 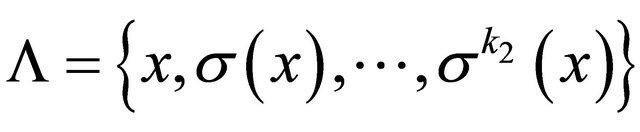 for some
for some 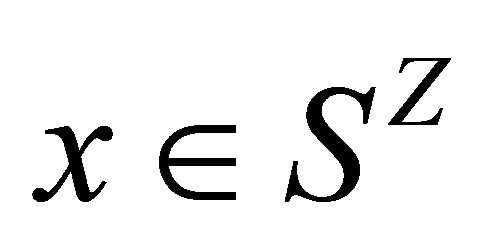 and
and . It is easy to be verified that
. It is easy to be verified that 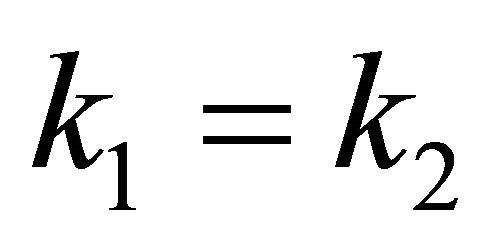 and they are common multiples of
and they are common multiples of ![]() and
and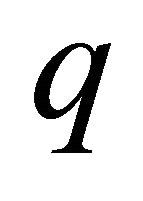 .
.
2.2. Transitivity Implies Density of Periodic Points
Theorem 2 Let  be a BSFT of a 1-D CA
be a BSFT of a 1-D CA 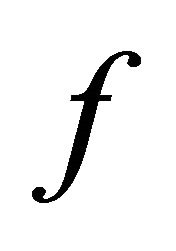 with
with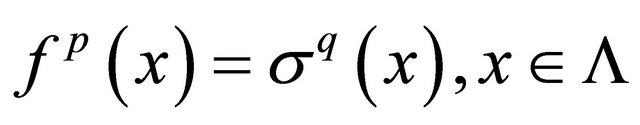 . If the shift
. If the shift  is transitive, then the set of periodic points of
is transitive, then the set of periodic points of 
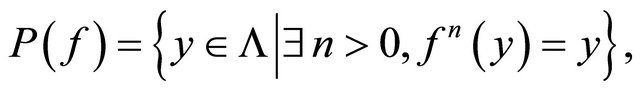 is dense in
is dense in .
.
Proof: Let 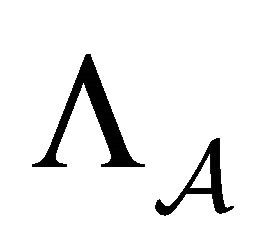 be the BSFT, and
be the BSFT, and  be its determinative block system. For any
be its determinative block system. For any 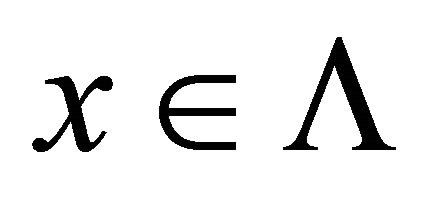 and
and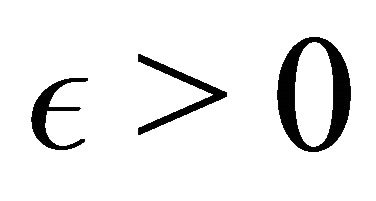 , there exists a positive integer
, there exists a positive integer  such that
such that
 and for
and for
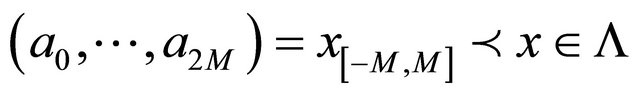 it follows that
it follows that
 .
.
Since ![]() is transitive on
is transitive on  there exists a path from
there exists a path from
 to
to  in the graph
in the graph
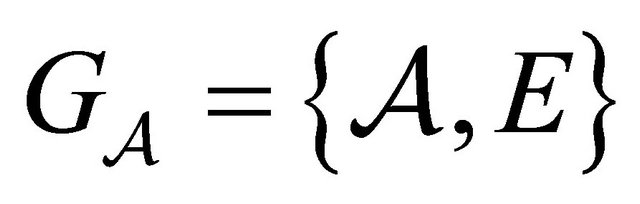 . Let
. Let

be the sequence corresponding to this path. Then, its any 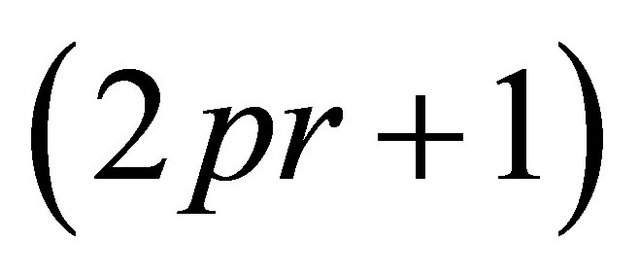 -subsequences belong to
-subsequences belong to .
.
Now, construct a cyclic configuration
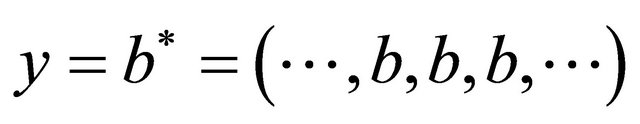 where
where
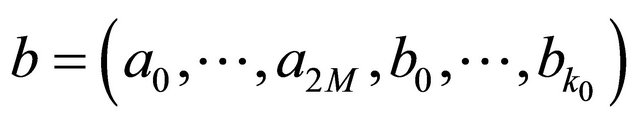 .
.
Obviously, 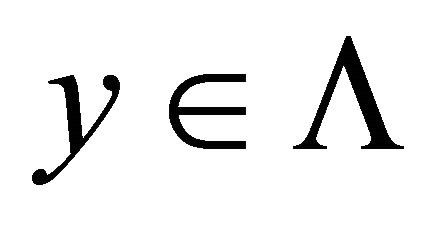 and
and , where
, where 
is the length of . Thus,
. Thus, 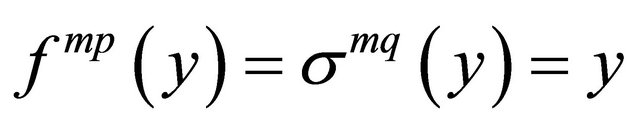 and
and , i.e.,
, i.e., 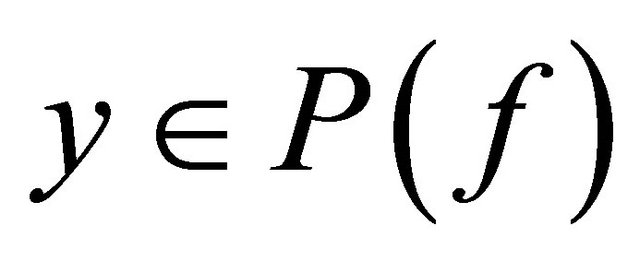 and
and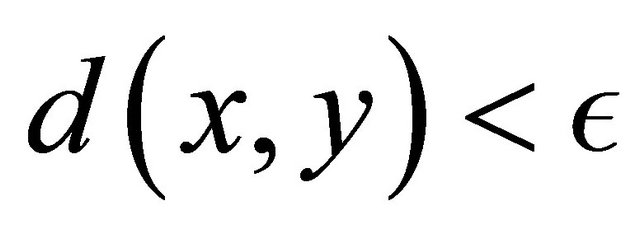 .
.
Therefore, the sets of periodic points  is dense in
is dense in .
.
By Theorem 2 and some results in [21], the following two theorems are obtained.
Theorem 3. If ![]() is transitive on a non-trivial BSFT of a 1-D CA
is transitive on a non-trivial BSFT of a 1-D CA , then
, then 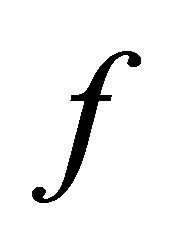 is sensitive on the BSFT.
is sensitive on the BSFT.
Theorem 4. A 1-D CA 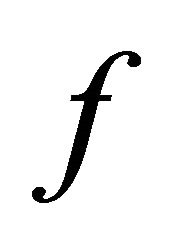 is chaotic in the sense of Devaney on its transitive non-trivial BSFT.
is chaotic in the sense of Devaney on its transitive non-trivial BSFT.
2.3. An Example of Transitive ECA Rule
Rule 26 is a member of Wolfram’s class IV and Chua’s hyper Bernoulli-shift rules, which defines many subsystems with rich and complex dynamics. This rule’s local map is 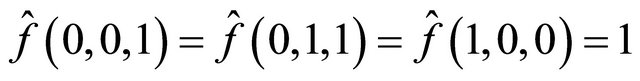 and
and
 for all other triples
for all other triples , and the corresponding global map is denoted by
, and the corresponding global map is denoted by 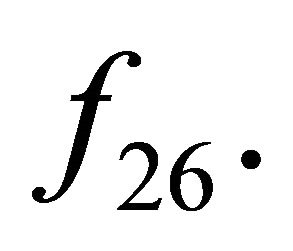
Proposition 3 There exists a BSFT of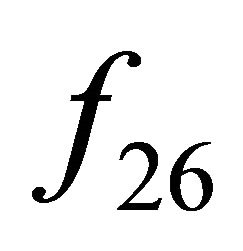 ,
,

such that , where
, where  and
and

Proof: Firstly,  is a closed set because
is a closed set because 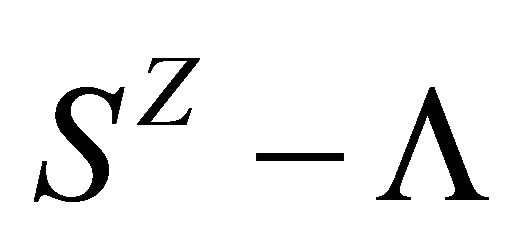 is an open set. Then, it can be easily verified that
is an open set. Then, it can be easily verified that 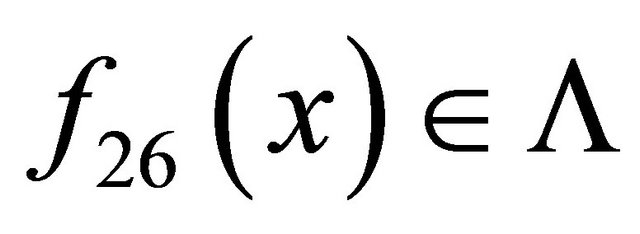 for any
for any  and
and  for any
for any
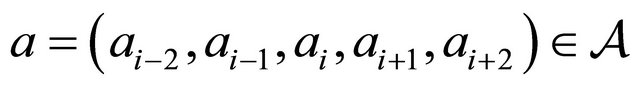 . This implies that
. This implies that
 for
for .
.
It is clear that the transition matrix corresponding to  is
is

Proposition 4. The transition matrix  is irreducible, so
is irreducible, so  is transitive on
is transitive on .
.
Proof: Let , where
, where  is the identity matrix, and let
is the identity matrix, and let 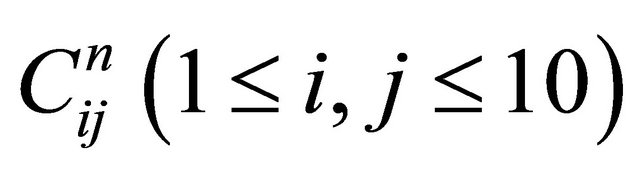 denote the elements of the power matrix
denote the elements of the power matrix . It can be easily verified that
. It can be easily verified that  for all
for all , so
, so 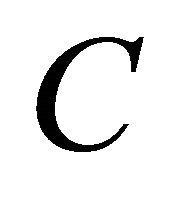 is aperiodic. Recall that a matrix
is aperiodic. Recall that a matrix  is irreducible if and only if
is irreducible if and only if 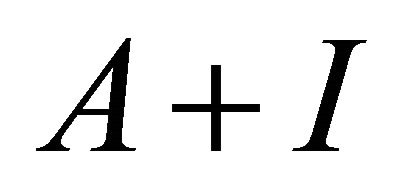 is aperiodic [23,24]. Hence,
is aperiodic [23,24]. Hence,  is irreducible and so
is irreducible and so 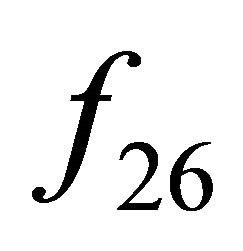 is transitive on
is transitive on .
.
Theorem 5 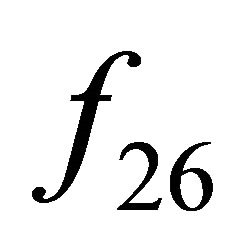 is chaotic in the sense of Devaney on
is chaotic in the sense of Devaney on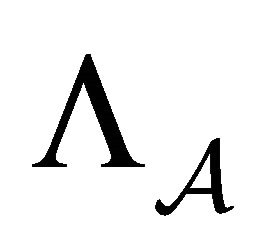 .
.
3. Conclusion
As a particular class of dynamical systems, CA have been widely used for modeling and simulating many physical phenomena. Despite their apparent simplicity, 1-D CA can display rich and complex evolutions, but many properties of their temporal evolutions are undecidable [25,26]. Although checking the transitivity based on its definition is very difficult [27], and it alone is not sufficient for chaos to exist in general dynamical systems, this work has rigorously proved that the shift transitivity implies the CA transitivity, and the CA with transitive non-trivial BSFT are chaotic in the sense of Devaney, partly answer the open question whether Devaney chaos in 1-D CA is equivalent to transitivity [28].
4. Acknowledgments
This research was jointly supported by the NSFC (Grants No. 11171084 and No. 60872093), the Hong Kong Research Grants Council (Grant No. CityU1117/10) and Foundation of Zhejiang Chinese Medical University (Grant No. 17211076).
REFERENCES
- J. von Neumann, “Theory of Self-Reproducing Automata,” University of Illinois Press, Urbana and London, 1966.
- M. Gardner, “The Fantastic Combinations of John Conway’s New Solitaire Game Life,” Scientific American, Vol. 223, No. 4, 1970, pp. 120-123. doi:10.1038/scientificamerican1070-120
- S. Wolfram, “Computation Theory of Cellular Automata,” Communications in Mathematical Physics, Vol. 96, No. 1, 1984, pp. 15-57. doi:10.1007/BF01217347
- S. Wolfram, “Theory and Application of Cellular Automata,” Word Scientific, Singapore Cty, 1986.
- S. Wolfram, “A New Kind of Science,” Wolfram Media, Inc., Champaign, 2002.
- G. A. Hedlund, “Endomorphisms and Automorphism of the Shift Dynamical System,” Mathematical System Theory, Vol. 3, No. 4, 1969, pp. 320-375. doi:10.1007/BF01691062
- L. O. Chua, V. I. Sbitnev and S. Yoon, “A Nonlinear Dynamics Perspective of Wolfram’s New Kind of Science, Part IV: From Bernoulli-Shift to 1/f Spectrum,” International Journal of Bifurcation and Chaos, Vol. 15, No. 4, 2005, pp. 1045-1183. doi:10.1142/S0218127405012995
- L. O. Chua, V. I. Sbitnev and S. Yoon, “A Nonlinear Dynamics Perspective of Wolfram’s New Kind of Scienc, Part VI: From Time-Reversible Attractors to the Arrows of Time,” International Journal of Bifurcation and Chaos, Vol. 16, No. 5, 2006, pp. 1097-1373. doi:10.1142/S0218127406015544
- L. O. Chua, J. B. Guan, I. S. Valery and J. Shin, “A Nonlinear Dynamics Perspective of Wolfram’s New Kind of Science, Part VII: Isle of Eden,” International Journal of Bifurcation and Chaos, Vol. 17, No. 9, 2007, pp. 2839- 3012. doi:10.1142/S0218127407019068
- L. O. Chua, K. Karacs, V. I. Sbitnev, J. B. Guan and J. Shin, “A Nonlinear Dynamics Perspective of Wolfram’s New Kind of Science, Part VIII: More Isles of Eden,” International Journal of Bifurcation and Chaos, Vol. 17, No. 11, 2007, pp. 3741-3894. doi:10.1142/S0218127407019901
- F. Y. Chen, W. F. Jin, G. R. Chen, F. F. Chen and L. Chen, “Chaos of Elementary Cellular Automata Rule 42 of Wolfram’s Class II,” Chaos, Vol. 19, No. 013140, 2009, pp. 1-6.
- W. F. Jin, F. Y. Chen, G. R. Chen, L. Chen and F. F. Chen, “Extending the Symbolic Dynamics of Chua’s Bernoulli-Shift Rule 56,” Journal of Cellular Automata, Vol. 5, No. 1-2, 2010, pp. 121-138.
- W. F. Jin, F. Y. Chen, G. R. Chen, L. Chen and F. F. Chen, “Complex Symbolic Dynamics of Chua’s Period-2 Rule 37,” Journal of Cellular Automata, Vol. 5, No. 4-5, 2010, pp. 315-331.
- F. F. Chen and F. Y. Chen, “Complex Dynamics of Cellular Automata Rule 119,” Physica A, Vol. 388, No. 6, 2009, pp. 984-990. doi:10.1016/j.physa.2008.12.002
- F. F. Chen, F. Y. Chen, G. R. Chen, W. F. Jin and L. Chen, “Symbolics Dynamics of Elementary Cellular Automata Rule 88,” Nonlinear Dynamics, Vol. 58, No. 1-2, 2009, pp. 431-442. doi:10.1007/s11071-009-9490-3
- L. Chen, F. Y. Chen, W. F. Jin, F. F. Chen and G. R. Chen, “Some Nonrobust Bernolli-Shift Rules,” International Journal of Bifurcation and Chaos, Vol. 19, No. 10, 2009, pp. 3407-3415. doi:10.1142/S0218127409024840
- F. Y. Chen, L. Shi, G. R. Chen and W. F. Jin, “Chaos and Gliders in Periodic Cellular Automaton Rule 62,” Journal of Cellular Automata, Vol. 7, No. 4, 2012, pp. 287-302.
- J. B. Guan, S. W. Shen, C. B. Tang and F. Y. Chen, “Extending Chua’s Global Equivalence Theorem on Wolfram’s New Kind of Science,” International Journal of Bifurcation and Chaos, Vol. 17, No. 12, 2007, pp. 4245- 4259. doi:10.1142/S0218127407019925
- R. L. Devaney, “An Introduction to Chaotic Dynamical Systems,” Addison-Wesley, Hazard, 1989.
- P. Favati, G. Lotti and L. Margara, “Additive One-Dimensional Cellular Automata Are Chaotic According to Devaney’s Definition of Chaos,” Theoretical Computer Science, Vol. 174, No. 1-2, 1997, pp. 157-170. doi:10.1016/S0304-3975(95)00022-4
- J. Banks, J. Brooks, G. Cairns, G. Davis and P. Stacey, “On the Devaney’s Definition of Chaos,” The American Mathematical Monthly, Vol. 99, No. 4, 1992, pp. 332-334. doi:10.2307/2324899
- B. Codenotti and L. Margara, “Transitive Cellular Automata Are Sensitive,” The American Mathematical Monthly, Vol. 103, No. 1, 1996, pp. 58-62. doi:10.2307/2975215
- B. Kitchens, “Symbolic Dynamics: One-Sided, Two-Sided and Countable State Markov Shifts,” Springer-Verlag, Berlin, 1998.
- Z. L. Zhou, “Symbolic Dynamics,” Shanghai Scientific and Technological Education Publishing House, Shanghai, 1997.
- J. Banks, “Regular Periodic Decompositions for Topologically Transitive Maps,” Ergodic Theory and Dynamical Systems, Vol. 17, No. 3, 1997, pp. 505-529. doi:10.1017/S0143385797069885
- K. Culik, L. P. Hurd and S. Yu, “Computation Theoretic Aspects of Cellular Automata,” Physica D, Vol. 45, No. 1-3, 1990, pp. 357-378. doi:10.1016/0167-2789(90)90194-T
- T. K. S. Moothathu, “Homogeneity of Surjective Cellular Automata,” Discrete Continuous Dynamic Systems, Vol. 13, No. 1, 2005, pp. 195-202.
- J. Kari, “Theory of Cellular Automata: A Survey,” Theoretical Computer Science, Vol. 334, No. 1, 2005, pp. 3-33. doi:10.1016/j.tcs.2004.11.021

