Advances in Microbiology
Vol.06 No.05(2016), Article ID:65972,17 pages
10.4236/aim.2016.65034
Effect of Small-Scale Turbulence on the Growth and Metabolism of Microcystis aeruginosa
Anne Wilkinson, Miki Hondzo, Michele Guala
St. Anthony Falls Laboratory, Department of Civil, Environmental and Geo-Engineering, College of Science and Engineering, University of Minnesota, Minneapolis, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 February 2016; accepted 24 April 2016; published 27 April 2016
ABSTRACT
Microcystis aeruginosa is a single-celled cyanobacterium, forming large colonies on the surface of freshwater ecosystems during summer, and producing a toxin (microcystin) that in high concentration can be harmful to humans and animals. These toxic effects can be governed by abiotic environmental conditions including water temperature, light, nutrient abundance, and fluid motion. We investigated the effect of small-scale turbulence on the growth and metabolism of Microcystis aeruginosa using field measurements and laboratory bioreactor investigations. The laboratory setup included two underwater speakers, generating a quasi-homogeneous turbulent flow with turbulent kinetic energy dissipation rates up to 10−6 m2/s3, comparable to field values in the lacustrine photic zone. The role of turbulence is quantified by comparing cell number, dissolved oxygen production/uptake, and inorganic carbon uptake in stagnant condition and two sets of experiments with turbulent conditions, quantified by the Taylor micro-scale Reynolds number at Reλ = 15 and Reλ = 33. The results suggest that turbulence mediates the metabolism of Microcystis aeruginosa measured by the net oxygen production, oxygen uptake, and inorganic carbon uptake. Furthermore, small-scale turbulence marginally influenced Microcystis growth rate estimated from cell population concentration (−5% and 11% for Reλ = 33 and Reλ = 15, respectively, as compared to stagnant conditions).
Keywords:
Harmful Algal Blooms, Microcystis aeruginosa, Cyanobacteria, Turbulence, Metabolic Response, Microcystin

1. Introduction
Cyanobacteria blooms are a ubiquitous nuisance in freshwater ecosystems throughout the world [1] . The cyanobacteria frequently dominate eutrophic lakes in summer months under high nutrient, warm, calm water conditions, where they can easily outcompete other aquatic microorganisms. Two unique adaptation strategies contribute to the dominance of cyanobacteria in these systems. First is the ability of individual cells to bond together into colonies. Second is the capability to regulate their buoyancy and thus their location with respect to the surface of the water column [2] [3] . Cyanobacteria blooms are of such interest not only because of the induced foul taste, odor and turbidity in lake water but also due to their contribution to hypoxia and subsequent fishery collapse [4] . Certain cyanobacteria, such as the Microcystis aeruginosa, produce a deadly liver toxin called microcystin. This compound has been regulated in drinking water by the World Health Organization (WHO), as it is a known carcinogen, gastrointestinal irritant and is responsible for animal deaths when present in high concentration [4] [5] . The production and utilization of microcystin by Microcystis has been widely studied, however evidence has not been entirely cohesive. Studies do point to the use of microcystin in competition with other organisms for dominance within aquatic system, for example: 1) aiding in intracellular inorganic carbon (Ci) regulation under low environmental Ci conditions to sustain photosynthetic processes [6] ; 2) inhibiting the metabolism of other microorganisms [7] , and 3) maintaining colonies through promotion of polysaccharide production [8] .
Microcystin production is only one of the competitive strategies that Microcystis can exhibit. Microcystis can persist in a broad range of environmental conditions where other microorganisms cannot, including cold temperatures [9] , low Ci conditions [10] , and in the presence of common herbicides [11] . Additionally, unlike many aquatic microorganisms, Microcystis remains photo-chemically active as they overwinter in the water column [9] . The authors reported that Microcystis react to environmental stressors, such as cold and dark water conditions, by reducing their metabolism. This behavior is known as a Type I stress response [12] . Microcystis have a photosynthetic metabolism and produces carbohydrates from Ci dissolved in the water and uses them for polysaccharide, RNA and nucleic acid production. Any excess Ci is released during the dark cycle during respiration. RNA and nucleic acids are primarily used in cell division, whereas polysaccharides are used in colony formation [13] . Thus, the availability of Ci is vital for the well-being of the Microcystis population. Microcystis can also adapt to varying levels of Ci within their environment through the utilization of a Carbon Concentrating Mechanism (CCM), which concentrates Ci on the primary CO2 fixing enzyme, RuBisCO [14] - [16] . This adaptation is essential for survival in periods of high productivity when Ci concentrations are low. Conversely, when the C:N ratio gets too high, and the Microcystis become nitrogen limited; they can sink excess Ci into extracellular polysaccharides (EPS) [17] [18] . For all these reasons, Ci concentration is a critical diagnostic variable when studying Microcystis growth and metabolism under different abiotic factors or environmental stresses.
Abiotic factors such as nutrient concentration, temperature, and photosynthetically active radiation (PAR) levels may define the necessary conditions for bloom initiation; however, hydrodynamics is recognized as a keycontrolling factor in the impact and extent of bloom persistence [19] . Microcystis are in fact exposed to a variety of fluid flow conditions, within their habitat, especially near the lake surface where they cluster during harmful algal bloom (HAB), and experience turbulent mixing effects by wind and waves [20] . Although many studies, discussed above, demonstrate Microcystis’ ability to adapt to their dynamic environment, the influence of hydrodynamics has not been thoroughly investigated. It has been shown that different microscopic algae react in different ways to the variability of fluid flow conditions. For instance, Chengala et al. (2013) [21] demonstrated that fluid motion facilitates favorable nutrient uptake for a green alga, Dunaliella primolecta, through the modification of the boundary layer around the cell. Kenis and Hoyt (1971) [22] and Jenkinson and Sun (2014) [23] showed that marine microalgae, planktonic algae, and bacteria produce EPS to increase drag reduction by locally modifying the viscosity of the ambient fluid.
Management and prediction of HAB formation and microcystin production require a comprehensive understanding of bloom mechanics and the response of microorganisms to the corresponding range of environmental conditions that occur in nature. Our particular objective is to investigate the metabolic and growth responses of Microcystis aeruginosa to different fluid flow conditions, consistent with observations in lacustrine environments. This is accomplished by evaluating the effect of turbulence based on careful monitoring of several physical and chemical variables including PAR, pH, alkalinity, dissolved oxygen (DO), and temperature as shown in Table 1, while varying the hydrodynamic forcing. Experiments were performed in a bioreactor actuated by two underwater speakers, designed to maintain a quasi-homogeneous isotropic turbulent flow with limited mean flow and mean shear, which can be well described by the Taylor micro-scale Reynolds number (Reλ). The fluid flow in the bioreactor was controlled to achieve comparable energy dissipation rates to those observed in the photic zone of Lake Minnetonka, Minneapolis, MN.
2. Materials and Methods
2.1. Speaker Reactor
The experimental setup, in Figure 1, is a submersible speaker bioreactor made from a 21.5 cm × 21.5 cm × 52 cm Plexiglas tank with two underwater speakers (AQ339 Aquasonic; Clark Synthesis, Littleton, CO, USA) positioned behind a mesh grid (1 cm2 mesh, 0.4 solidity) at each end. This experimental apparatus is also used in Chengala et al. (2013). The fluid motion in this setup is generated by the vibration of the speaker diaphragm, which pushes the fluid through the grid. The speakers were out of phase with each other by 180˚ (reverse polarity), therefore, when the left speaker contracted, the right speaker expanded, allowing for the continuous generation of eddies into the test section. The speakers can generate different flow conditions by actuating sinusoidal signals of varying prescribed frequencies (Hz) and amplitudes (V). A programmable Labview (National Instruments, Austin, TX, USA) function generator connected to an amplifier (Samson Servo 300, Samson Technologies, Hauppauge, New York, USA) generates the speaker signals. The bioreactor is completely enclosed and slightly pressurized. All instruments and adjustments are made in situ. A magnetic scraper (ProMag, Aqueon, Franklin, WI, USA) was employed before cell counts at the bottom of the tank to re-suspend settled cells and ensure proper cell concentration measurements.
2.2. Initial Experimental Conditions
Each experiment used a 14:10 hour light-dark cycle from simulated solar fluorescent lights (Phillips Plant and Aquarium 20 W, Phillips, Andover, MA, USA) positioned on each side of bioreactor parallel to the main aquarium axis and perpendicular to the speaker orientation to ensure uniform vertical light exposure, and prevent light dependent algal distribution. The PAR was measured near the tank every 5 minutes during the experiment by a spherical quantum sensor (LI-193 LICOR, Lincoln, NE, USA) yielding an average 58.3 ± 4.4 (μmol/m2∙s) during the light cycle and 39.7 ± 1.4 (μmol/m2∙s) during the dark period. The fluid temperature was monitored every five minutes in conjuncture with the DO measurements by an optical oxygen and temperature sensor (Optode 3835 Aanderaa Data Instruments AS, Bergen, Norway) yielding an average temperature of 23.03˚C ± 1.86˚C.
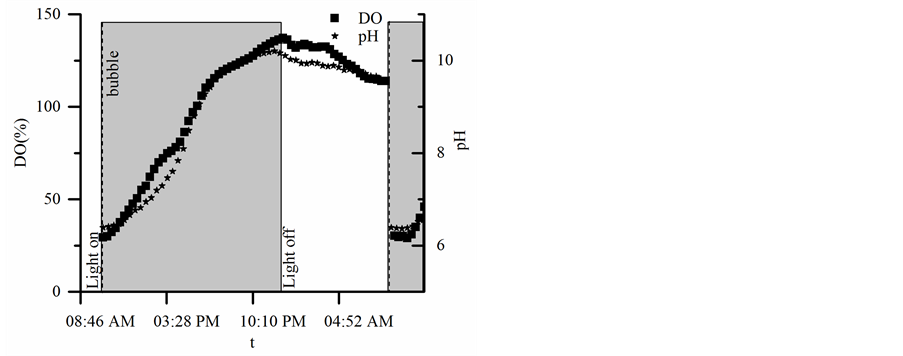
After an equilibration period, the pH was adjusted (day 4 - 11) to 5.8 - 6.2, as shown in Figure 2, by bubbling industrial grade CO2 gas (Matheson Gas, New Brighton, MN, USA) using a 23 in. air curtain diffuser (Elite Pet Supplies, Vineyard, NSW, Australia). The addition of CO2 to the system increases the growth rate as compared to the estimated growth rate of samples without CO2 adjustment (observed by Qiu and Gao, 2002 [24] and confirmed in our preliminary experiments). On days 3 - 11, the DO saturation was reduced to 20% - 30% daily immediately following the pH adjustment, also shown in Figure 2, by bubbling industrial grade N2 gas (Matheson Gas, New Brighton, MN, USA) through the same diffuser. Both environmental adjustments, pH and DO, had to be made because of the lack of gas exchange in the bioreactor, as it is a closed system. As discussed above, access
Table 1. Comparison of average environmental conditions in the laboratory bioreactor and Lake Minnetonka, MN. The Lake Minnetonka data consist of time and depth-averaged values within the photic zone (0.5 - 1.5 m) at 10-10:30 am, see Appendix. The laboratory bioreactor data report time averaged values obtained during the maximum daily growth period (11 am-1 pm) for all lab experiments, for all days.
Figure 1. Schematic overview of the speaker reactor setup. (a) Speaker reactor schematic detailing the positions of the PIV planes, the sampling location representing the positions of the instruments (i, chlorophyll probe, ii, DO probe, iii, pH meter), the origin and the orientation of the (x,y) reference system, the position of the back light, and orientation of the speakers with respect to the grid. (b) Top view schematic showing the orientation of the PIV planes with respect to the instrument locations and the sampling hole (iv).
Figure 2. An example of daily light, DO and pH adjustments, the dashed line symbolizes when the CO2 and N2 gasses were bubbled, and the gray box represents the light cycle. As can be seen after the bubbling of N2 and CO2, the DO and pH are reduced to daily initial conditions (~9 am).
to Ci is vital for the health of the population. The DO adjustment is made to prevent photo-oxidative death, in which too much oxygen and light can cause chlorophyll bleaching and premature population die off, especially in low Ci conditions [25] [26] .
2.3. Flow Measurement Setup
The fluid motion within the bioreactor was quantified by non-intrusive two-dimensional (2D) Particle Image Velocimetry (PIV) in which small tracer particles are illuminated by a laser sheet and tracked through a series of high-speed images. The system comprised of a high speed camera (VC-4MC-M180E0 Viewworks, Anyang, Gyeonggi, Republic of Korea), fitted with Nikon AF 50mm lens (Nikon, Tokyo, Japan), with a resolution of 2048 × 2048 pixels, able to capture 1000 images at 30 frames per second within a field of view of 7 cm × 7 cm. The tracer particles were 8 - 12 μm hollow glass spheres (1.05 g∙cm−3) and were illuminated by ND:YAG pulsed green laser (LPY 700 series Litron, Rugby England, UK). The laser and the camera were synchronized (TSI LaserPulse, Shoreview, MN, USA) and controlled by Insight 4G software (TSI, MN) that processed the images to derive 2D velocity fields; u, and v, oriented according to Figure 1. The flow was measured in four planes without
the presence of Microcystis, for two speaker settings (50 Hz frequency, at 0.2 V amplitude and 30 Hz at 0.2 V). Based on symmetry considerations, flow statistics averaged over the four planes are considered representative of the full aquarium.
2.4. Fluid Flow Analysis
The experimental apparatus was designed to mimic environmental flows at laboratory scale under controlled and monitored conditions. Spatio-temporally resolved velocity fields were measured by PIV, see Figure 3, to adequately quantify turbulent characteristics in each experimental case, respectively identified by: the Reynolds number, Reλ = (urmsλ)/ν (where urms is the root mean square velocity, Taylor micro-scale (λ), and ν is the kinematic viscosity), the rate of energy dissipation (ε), and the Kolmogorov length scale (η). The Reynolds number based on the Taylor micro-scale is often used to describe homogeneous turbulence (e.g. [27] ).
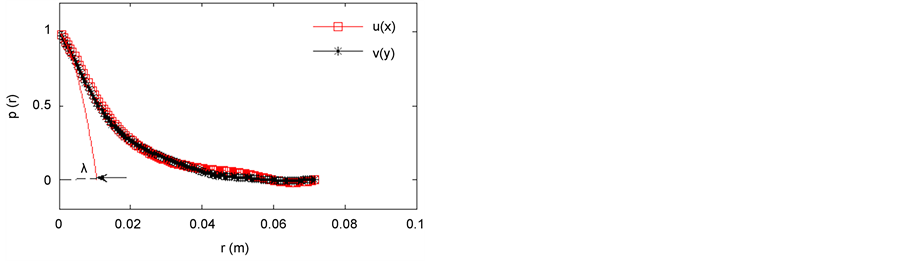
The Taylor micro-scale, λ, is the intermediate length scale characterizing homogeneous and isotropic turbulence, in between the integral length scale (Lx,y) and the Kolmogorov length scale. Physically it defines the upper limit of the region where viscosity is still relevant to turbulent eddy formation. The Taylor micro-scale in this study was estimated in two ways: 1) using Equation (1), requiring an estimate of ε (hence the notation λε), 2) using the autocorrelation of fluctuating velocity components, u(x) or v(y), as shown in Figure 4, simply referred to as λ.
Here the autocorrelation function is defined for homogeneous isotropic turbulence as 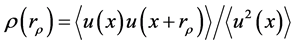 , where u(x) is the velocity fluctuation, rρ is the spatial lag, and the
, where u(x) is the velocity fluctuation, rρ is the spatial lag, and the  expression indicates spatial averaging along any x coordinate (e.g. [28] ).
expression indicates spatial averaging along any x coordinate (e.g. [28] ).
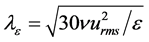 (1)
(1)
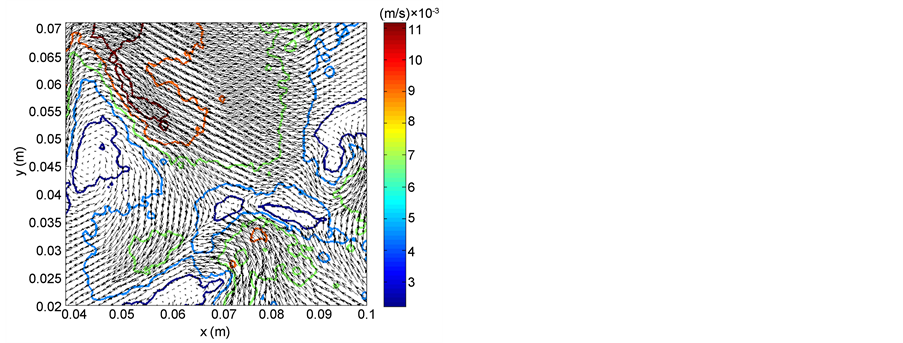
Figure 3. Sample instantaneous velocity vector field in the speaker reactor at Reλ = 33. x and y are based on the origin shown in Figure 1. The contours represent the magnitude of the (u,v) velocity vectors (m/s).
where the rate of energy dissipation can be estimated using the two-dimensional (2D) spatial velocity derivatives [21] [29] [30]
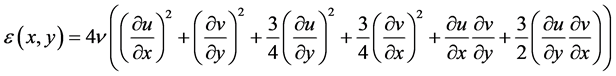 (2)
(2)
A relevant turbulent length scale for phytoplankton growth and nutrient uptake in quasi-homogeneous turbu-
lence is the Kolmogorov scale, 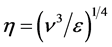 [21] . It represents the scale of the smallest eddies in the flow,
[21] . It represents the scale of the smallest eddies in the flow,
where turbulent kinetic energy is eventually dissipated into heat and defines the lower limit of the inertial range.
Agreement between λε and λ, shown in Table 2, indicates consistency between the velocity autocorrelation and the estimation of ε(x,y), based on spatial velocity derivatives, supporting both the quality of the flow measurements and the homogeneity of the flow. Although the Reynolds number is relatively small [27] there is strong agreement with the turbulence intensities observed in Lake Minnetonka in the presence of cyanobacteria near the surface of the water column (see Appendix).
Evidence of Homogeneity and Isotropy
As can be seen in Figure 5(a), the energy dissipation rate is relatively uniform in the vertical profile with the exception of Reλ = 33, near the wall. This supports our effort to generate quasi-homogeneous turbulence within the bioreactor. Additionally, evidence of homogeneity can be seen in Figure 5(b), as the autocorrelation curves obtained for different PIV planes are fairly consistent. Evidence of isotropic turbulence shown in Table 2 include: 1) the ratio of velocity fluctuations urms/vrms~1, 2) the autocorrelation curves are illustrated in Figure 4 and the resulting estimates of the integral length scales are independent of the directions, u(x), v(y) along which
statistics are computed: Lx/Ly = 1.01, 0.93 for the Reλ = 33, and 15 respectively. Note that the integral length scales, Lx, Ly, calculated from the integral of the corresponding normalized autocorrelation curves, represent the largest, statistically significant, eddy in the turbulent flow.
Figure 4. Spatial autocorrelation function of the horizontal and vertical velocity components along the vertical (y) and the transverse (x) directions of the bioreactor setup (Reλ = 33) showing how the fit parabola yields the estimate of the Taylor micro-scale, λ, represented by the black arrow.
Table 2. Flow characteristics in the speaker reactor and at the Lake Minnetonka measurement site. The values for urms, vrms and ε are spatially averaged over the PIV planes (30 Hz 1B, 2A planes, 50 Hz all planes), described in the fluid characterization section. A detailed description of Lake Minnetonka data analysis is in Appendix.
Figure 5. Evidence of isotropy in the speaker reactora) Vertical Profile of energy dissipation rate, ε, (Reλ = 33 and 15). The vertical profile of the energy dissipation rate is estimated by averaging, along the x direction, the median of the time history ε(x,y,t), determined from Equation (2) (Reλ = 15, planes 1B, 2A, and Reλ = 33 all planes). (b) Normalized autocorrelation of u(x) estimated for all PIV planes at Reλ = 33.
2.5. Microcystis Culture and Analysis
The Microcystis aeruginosa strain B3-R-7 was obtained by the Department of Fisheries and Allied Aquacultures, Auburn University, Alabama. The cultures were maintained in tanks in the presence of 1:50 BG-11 media dilution (Sigma-3061, Sigma-Aldrich, St Louis, MO, USA) and Mili-Q water (Millipore, Billerica, MA, USA) and exposed to natural light. Samples taken from this culture were diluted in fresh growth media, allowed to grow for 4 - 8 days, to ensure they were within the exponential growth phase. The speaker reactor was then inoculated with an initial concentration of 100,000 cells/mL from this culture. Three depth-averaged samples (9 mL) were taken from the top of the tank by inserting a plastic tube into the bioreactor, then blocking the top of the tube and extracting a sample. Samples were taken once per day (day 1 - 11), each morning after the pH and oxygen saturation were adjusted. The cell concentration was estimated using the average of triplicate cell counts using a hemocytometer. Statistical analysis of cell concentration data were analyzed using a two-way ANOVA with replication with factors (turbulence level and time) with an α = 0.05 using Microsoft Office Excel 2010 (Redmond, WA, USA).
Growth rate for the full experimental cycle can be estimated using the Verhulst logistic equation for population-limited growth, below [31] [32] :
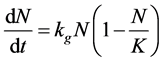 (3)
(3)
where N is the cell concentration, t is time, kg is the growth rate, and K is the carrying capacity.
A second method for assessing Microcystis concentration and growth is based on chlorophyll measurements. The fluorometer (Cyclops 7, Turner Designs, Sunnyvale, CA, USA) was employed to measure the chlorophyll a (Chla) within the tank, after a calibration procedure. From the fluorometer output (V), cell concentration data during the dark cycle can be obtained by the calibration curve (data not shown).
2.6. Dissolved Ci and DO Data
DO production, Ci, and DO uptake are indicators of photosynthetic activity and can reveal critical information on Microcystis’ cellular metabolism [33] . The Ci can be calculated from Equation (4) by measuring the alkalinity and the pH within the speaker reactor. The pH of the system was taken in situ every five minutes with a pH meter (pHASE, SensorX, Garden Grove, CA, USA) connected to a transmitter (TX100pH/mV 2 wire, SensorX, Garden Grove ,CA, USA), which is logged by a Labview program. The alkalinity was measured twice per day (on days 4 - 10), once in the morning after pH and oxygen adjustment and again in the evening (6 hours later). The alkalinity measurements using 100 mL depth averaged samples were titrated following the standard operating procedure (SOP) WQ/WC 202.1 (USDA/ARS-Stuttgart National Aquaculture Research Center, Almyra, AR, USA). The titrant used was a standardized 0.02N H2SO4, prepared according to the reagent preparation in the SOP, from carbon dioxide free water and H2SO4 (ACS grade, BDH H3070, VWR, Radnor PA, USA). The pH and alkalinity measurements allow for Ci calculation through the carbonate cycle for a closed system.
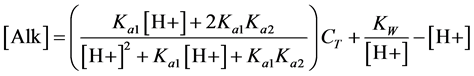 (4)
(4)
where [Alk] is the alkalinity, CT is the total Ci, [H+] = 10-pH, Ka1 = 10-6.35, Ka2 = 10-10.33, Kw = 10-14 at 25˚C and 1 bar [34] .
The flux of Ci, 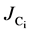 , was calculated using the change in total Ci over the relevant daily growth period (~6 hours into the light cycle), using Equation (5):
, was calculated using the change in total Ci over the relevant daily growth period (~6 hours into the light cycle), using Equation (5):
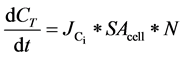
where SAcell is the cell surface area. The SAcell was estimated based on measured cell equivalent radius [35] .
Although both alkalinity and pH are necessary for Ci calculations in a closed system, pH time series data can give a qualitative measure of the Ci uptake during the light cycle (photosynthesis) and Ci production in the dark cycle (respiration). The lower the pH, the more Ci is present in the system due to the transformation of dissolved CO2 gas to carbonic acid. Thus, when the Microcystis remove Ci from the water during photosynthesis, the pH increases as observed in Figure 6(a). The CO2 is not added until day 4 and the pH response is not as rapid as observed during the exponential growth period. This is due to the lower cell concentration in lag phase when the Microcystis population has not yet reached exponential growth. This trend is observed at both Reλ. As discussed above, CO2 adjustments were enforced when the pH was above 5.8 - 6.2, ensuring that at the beginning of every day Microcystis were exposed to the same environmental conditions, pH, DO, and temperature.
DO was measured, in situ, at 5 minute increments using an optical oxygen and temperature sensor, as discussed above. The flux of oxygen, JDO, was computed using the slope of the oxygen time series, (d(DO))/dt ((DO mol)/(L×min)), estimated in the following time period: 5 hours after initial condition adjustment for net photosynthetic oxygen production, up to 5 hours prior to the adjustment for respiratory oxygen uptake.
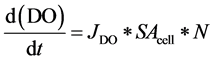
These fluxes represent the average net production of oxygen for each Microcystis cell during the day (JDOprod) and the corresponding average uptake of DO during the night (JDOupt). As shown in Figure 6(b), diurnal oxygen production (net photosynthesis) and uptake (respiration) occurred throughout the exponential growth phase, which is to be expected with photosynthetic organisms. During the daily growth interval, the oxygen concentration
Figure 6. Example DO and pH time series for the three experimental conditions investigated (stagnant Reλ = 33 and 15). The arrows indicate when the N2 and CO2 were bubbled to adjust the DO and pH in the bioreactor.
reached super-saturation, thus requiring nitrogen bubbling to avoid damage to cell population.
3. Results
3.1. Microcystis Population Data
The population growth of Microcystis is shown in Figure 7. The range of cell concentration observed in this experiment was from 1 × 105 cells/mL to 17 × 106 cells/mL and was well within the high-risk range for HAB established by the WHO [4] . From Equation (3), the average estimated kg were 0.62 (r2 = 0.97), 0.59 (r2 = 0.97), and 0.69 (r2 = 0.97) (1/day) for stagnant, Reλ = 33, and Reλ = 15 respectively. The estimates indicate that the highest turbulence level, Reλ = 33, yielded the lowest growth rate by 5% compared to the stagnant condition, while the Reλ = 15 condition increased kg by 11%. These results were corroborated by estimation of kg using first order growth kinetics for the exponential growth phase days 1 - 9 and the same trend between the stagnant and turbulent experiments is observed.
From Figure 7, we can establish three growth phases within the 11-day experiments using the theoretical growth curve: lag phase (days 0 - 4), exponential phase (days 5 - 9) and the transition to the stationary phase (day 10 - 11). A two-way ANOVA was performed on the cell concentration times series considering turbulence regimes (factor A), and time (factor B). The cell counts for each day, (n = 9 cell counts/day) represent the three replicate experiments. ANOVA analysis yielded a P < 0.05 with α = 0.05 for the investigated cell concentration time series. The analysis indicates that with 95% confidence the difference in cell concentration among the stagnant and turbulent regimes (stagnant, Reλ = 33, and Reλ = 15) are statistically significant. However, the kg values estimated from these cell concentration time series showed only marginal differences in population growth rate among the experimental conditions, as stated above.
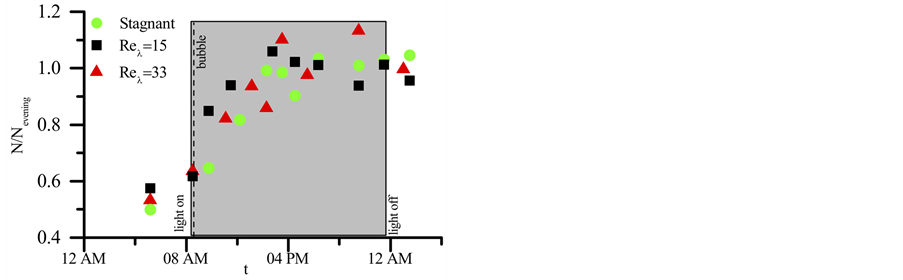
A series of 24-hour cell concentration measurements were conducted to define the daily growth interval and the relevant time frame for the metabolic flux calculations. Figure 8 shows the daily evolution of cell growth for Microcystis during a 24-hour period at the beginning of the exponential growth phase under different Reλ. The Microcystis population experiences linear growth within the first 5 hours (9:00 am-2:00 pm) of the light cycle and
Figure 7. Population growth of Microcystis for stagnant, Reλ = 15 and Reλ = 33, sampled at the beginning of the light cycle. The mean cell concentrations are calculated from daily measurements (3 samples/day) of triplicate experiments, (n = 9). The vertical bars represent standard deviation calculated from the nine data points per day. (a) Denotes the beginning of the exponential growth phase (b) denotes the start of the stationary phase. The dotted line represents the theoretical growth curve based on the verhulst equation, Equation (3), fitted on all experimental growth measurements.
Figure 8. Cell concentration, N, measured at smaller time intervals within a 24 hour period at the start of the exponential growth phase (day 5) normalized by average cell concentration for the evening period of the constant cell population (4 pm-1 am). The gray region represents the light cycle, and the dashed line represents the O2 saturation and pH adjustment is made.
then ceases growth, thereafter. The daily growth interval within the 24-hour period appears to be independent of the tested Reλ.
3.2. Oxygen Fluxes
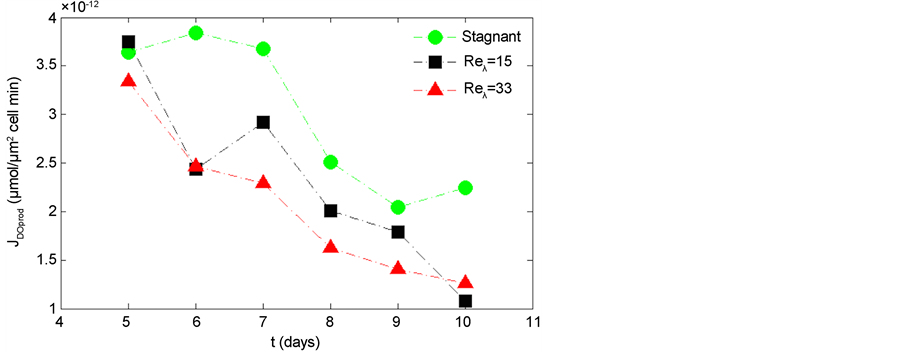
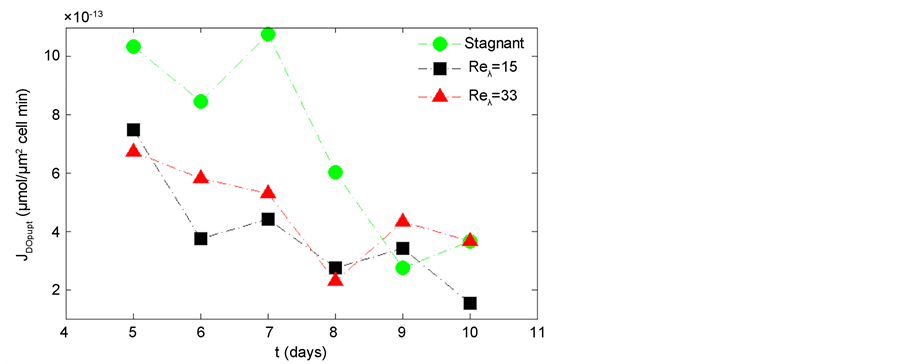
The net DO production during photosynthesis is shown in Figure 9. The net DO production, JDOprod, for the stagnant condition is consistently higher than that of turbulent cases (Reλ = 15, and 33). The results indicate a hindrance of photosynthesis due to environmental conditions induced by the fluid flow. The overall decline of net DO production in each case reflects the transition from the exponential growth phase to the stationary phase. However, all turbulent levels decline at similar slopes throughout the experiment. The DO uptake during respiration is shown in Figure 10. The stagnant condition shows consistently higher JDOupt and has a steeper slope during the exponential growth phase (days 5 - 8), as compared to the turbulent conditions.
3.3. Inorganic Carbon Fluxes
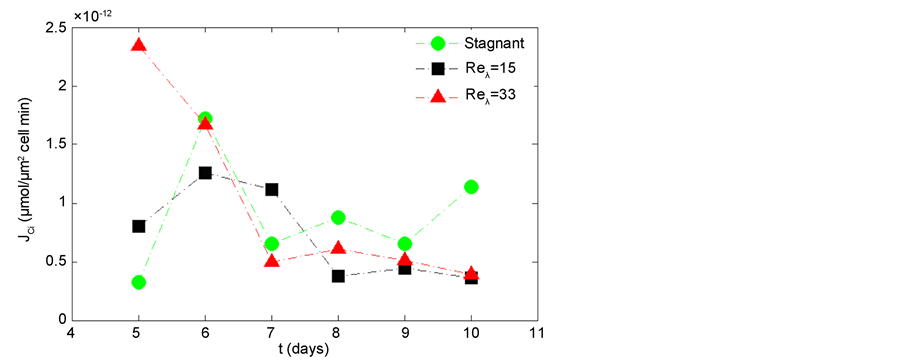
As seen in Figure 11, the stagnant and Reλ = 15 conditions appear to have a constant carbon uptake flux, where as, the Reλ = 33 manifests a decreasing trend. Both turbulent cases are lower in comparison to the stagnant condition at the end of exponential growth and stationary growth phase (days 8 - 10). For days 8 - 10, the Ci uptake for the turbulent case (Reλ = 15 and Reλ = 33), on average, is 44.3%, 56.8% of the stagnant condition for Reλ = 33, 15, respectively. Qiu and Gao, (2002) [24] have reported asimilar difference in photosynthesis for Microcystis due to various Ci availability.
4. Discussion
Thomas and Gibson (1990) [36] suggested that cyanobacteria are relatively less sensitive to turbulence compared to other micro-algal groups. Additionally, the effect of small-scale turbulence has been shown to be less of a controlling factor on population growth, as compared to its contribution to turbulent mixing, such as entrainment of CO2 from the atmosphere and the change in lighting conditions due to physical displacement of the
Figure 9. Oxygen production flux in the stagnant, Reλ = 15, and Reλ = 33 conditions. The data points represent an average of the triplicate experiments.
Figure 10. Oxygen uptake flux in stagnant, Reλ = 15, and Reλ = 33 conditions. The data points represent an average of triplicate experiments.
Figure 11. Comparison of dissolved inorganic carbon, Ci, uptake flux for stagnant, Reλ = 33, and Reλ = 15. The data points are obtained from Equations (4), (5) using averaged measurements of alkalinity and pH during one experiment for each Reλ.
Microcystis within the water column [2] [19] [37] . Although the population growth appears to be only marginally influenced by small-scale turbulent conditions, our study highlights an appreciable mediation of the photosynthetic metabolism by turbulence, independent of the influence of CO2 entrainment into the water, DO or nutrients abundance, and changes in PAR availability. The observed mediation of photosynthesis is a genuine stress response similar to Microcystis’ response to cold and dark conditions, low environmental Ci concentrations, and other common environmental stressor experienced by Microcystis [10] [24] [38] . For example, Chen et al. (2015) [39] reported sodium chloride contamination inhibits photosynthesis in Microcystis aeruginosa by suppressing carbon assimilation. To facilitate the discussion of our findings in relation to different fluid flow conditions, we first highlight some relevant metabolic processes of Microcystis.
Microcystis are photosynthetic cyanobacteria, thus, they derive their carbohydrates from Ci dissolved in the water, which they use to produce several biochemical compounds, including microcystin and EPS. Thus, the Cithat has been taken up through photosynthesis but is not released during respiration is accumulated and utilized by the cell. Under stagnant fluid conditions, Ci uptake is the same for days 5 - 7 and higher for days 8 - 10, compared to the turbulent conditions. However, the respiration is higher at days 5 - 8 (~exponential growth) and then the same for days 9 - 10 (~stationary phase) for the stagnant condition, again as compared to the turbulent conditions. This demonstrates a change from accumulation of Ci under turbulent condition in the exponential growth phase (where the cell is taking up the same Ci but respiring less compared to the stagnant condition) to the accumulation of Ci under stagnant condition (where the cell is taking up more Ci and respiring at the same rate compared to the turbulent) during the stationary phase. We hypothesize the difference in Ci accumulation during the exponential growth is due to EPS production, utilized to form a protective layer around the cell and reduce drag in the presence of the turbulence. Several studies have demonstrated that dilute polymer solutions produced by microalgae act as drag reducers and are inferred to be a physiological response to mediate mechanical damage to the cell due to turbulence stress [22] [23] [40] . It is observed that there is a switch from Ci accumulation in the turbulent case exhibited during exponential growth phase to the Ci accumulation observed in the stagnant condition during stationary growth phase. As stated in the previous section, Microcystis use EPS as a sink for Ci to combat nitrogen deficiencies that would be present in the stationary growth phase, due to depleted nutrients. The marked increase in Ci uptake is supported by the observation that EPS production during nitrogen stress is 3 - 4 times greater than that produced to reduce drag [40] . The observed transient effect of Ci accumulation between the exponential growth phase and the stationary phase is further supported by the fact that, EPS structure and composition evolve throughout the growth cycle [41] . An additional explanation for the increased Ci uptake during the stationary phase could be that Ci is used for the production of microcystin. Presumably, the Microcystis produce additional microcystin as a self-defense mechanism during the nutrient limiting stationary phase [7] .
The reduction in net DO production in the turbulent flow could be related to the way Microcystis uniquely respond to stress. Wu et al. (2008) [9] demonstrated that Microcystis, under such conditions, responded by reducing their metabolism, while maintaining their cell population, i.e. not growing exponentially. It could be that the Microcystis under turbulence-induced stress, not only can reduce their metabolism, as seen in Figure 9, but also grow exponentially. The incremental change in metabolic response to turbulence can be explained by the resilience of Microcystis, which have been shown to be more resistant to changes in their environment [19] [37] . The effect of additional turbulent stress in conjuncture with other environmental factors has not been investigated thoroughly, and it is possible that additional turbulent stress interrupts physiological processes.
5. Conclusion
Small-scale turbulence, in controlled laboratory experiments, has been observed to affect metabolic photosynthesis of Microcystis, by inducing a reduction in net oxygen production and uptake, and a moderation of the carbon uptake. These effects were observed at different growth phases of the Microcystis, even if the actual population growth rate estimated from the cell concentration was only slightly modulated by turbulence (−5% and 11% for Reλ = 33 and Reλ = 15, respectively, as compared to stagnant conditions). The reduced photosynthesis can be explained by the conjecture that Microcystis reduce their metabolism under different stress conditions. While the increased accumulation of Ci in the turbulent cases, during the exponential growth phase, provides evidence of Microcystis’ ability to produce EPS, decrease drag and prevent cellular damage. Subsequently, the increased Ci uptake in the stationary phase in the stagnant condition may be attributed to the production of EPS to compensate for low nitrogen availability. The decreased Ci uptake in the stationary phase in the turbulent flow could be attributed to metabolic stress manifested by decreased net oxygen production (Figure 9).
Acknowledgements
The authors would like to gratefully acknowledge Alan Wilson and the Department of Fisheries and Allied Aquacultures, Auburn University, Alabama for providing the initial culture samples. We would also like to recognize the generosity of the Lake Minnehaha Watershed district in providing a boat and guide for the field data collected from Lake Minnetonka, Minnesota in August 2014. We acknowledge critical input from Prof. William Arnold in the estimate of inorganic carbon in the bioreactor. Partial funding for this study is provided by the Legislative-Citizen Commission on Minnesota Resources (LCCMR), Environment and Natural Resources Trust Fund 2015-2016, Assessing the Increasing Harmful Algal Blooms in Minnesota Lakes, ID: 038-B.
Cite this paper
Anne Wilkinson,Miki Hondzo,Michele Guala, (2016) Effect of Small-Scale Turbulence on the Growth and Metabolism of Microcystis aeruginosa. Advances in Microbiology,06,351-367. doi: 10.4236/aim.2016.65034
References
- 1. van Gremberghe, I., Leliaert, F., Mergeay, J., Vanormelingen, P., Van der Gucht, K., Debeer, A.-E., Lacerot, G., De Meester, L. and Vyverman, W. (2011) Lack of Phylogeographic Structure in the Freshwater Cyan Bacterium Microcystis aeruginosa Suggests Global Dispersal. PloS One, 6, 1-12.
http://dx.doi.org/10.1371/journal.pone.0019561 - 2. Carey, C.C., Ibelings, B.W., Hoffmann, E.P., Hamilton, D.P. and Brookes, J.D. (2012) Eco-Physiological Adaptations That Favour Freshwater Cyanobacteria in a Changing Climate. Water Research, 46, 1394-1407.
http://dx.doi.org/10.1016/j.watres.2011.12.016 - 3. Paerl, H.W., Fulton, R.S., Moisander, P.H. and Dyble, J. (2001) Harmful Freshwater Algal Blooms, with an Emphasis on Cyanobacteria. Scientific World Journal, 1, 76-113.
http://dx.doi.org/10.1100/tsw.2001.16 - 4. Paerl, H.W. and Otten, T.G. (2013) Harmful Cyanobacterial Blooms: Causes, Consequences, and Controls. Microbial Ecology, 65, 995-1010.
http://dx.doi.org/10.1007/s00248-012-0159-y - 5. World Health Organization (2008) Guidelines for Water Quality. Vol.1, 3rd Edition Incorporating 1st and 2nd Addenda. World Health Organization, 1, 1-144.
- 6. Jahnichen, S., Ihle, T., Petzoldt, T. and Benndorf, J. (2007) Impact of Inorganic Carbon Availability on Microcystin Production by Microcystis aeruginosa PCC 7806. Applied and Environmental Microbiology, 73, 6994-7002.
http://dx.doi.org/10.1128/AEM.01253-07 - 7. Singh, D.P., Tyagi, M.B., Kumar, A., Thakur, J.K. and Kumar, A. (2001) Antialgal Activity of a Hepatotoxin-Producing Cyanobacterium, Microcystis aeruginosa. World Journal of Microbiology and Biotechnology, 17, 15-22.
http://dx.doi.org/10.1023/A:1016622414140 - 8. Gan, N., Xiao, Y., Zhu, L., Wu, Z., Liu, J., Hu, C. and Song, L. (2012) The Role of Microcystins in Maintaining Colonies of Bloom-Forming Microcystis spp.: Microcystis Colony Maintenance by Microcystins. Environmental Microbiology, 14, 730-742.
http://dx.doi.org/10.1111/j.1462-2920.2011.02624.x - 9. Wu, Z., Song, L. and Li, R. (2008) Different Tolerances and Responses to Low Temperature and Darkness between Waterbloom Forming cyanobacterium Microcystis and a Green Alga Scenedesmus. Hydrobiologia, 596, 47-55.
http://dx.doi.org/10.1007/s10750-007-9056-7 - 10. Yamamoto, Y. and Nakahara, H. (2005) Competitive Dominance of the Cyanobacterium Microcystis aeruginosa in Nutrient-Rich Culture Conditions with Special Reference to Dissolved Inorganic Carbon Uptake. Phycological Research, 53, 201-208.
http://dx.doi.org/10.1111/j.1440-1835.2005.tb00372.x - 11. Lürling, M. and Roessink, I. (2006) On the Way to Cyanobacterial Blooms: Impact of the Herbicide Metribuzin on the Competition between a Green Alga (Scenedesmus) and a Cyanobacterium (Microcystis). Chemosphere, 65, 618-626.
http://dx.doi.org/10.1016/j.chemosphere.2006.01.073 - 12. Zhang, M., Kong, F., Shi, X., Xing, P. and Tan, X. (2007) Differences in Responses to Darkness between Microcystis aeruginosa and Chlorella pyrenoidosa. Journal of Freshwater Ecology, 22, 93-99.
http://dx.doi.org/10.1080/02705060.2007.9664149 - 13. Li, M., Nkrumah, P. and Xiao, M. (2014) Biochemical Composition of Microcystis aeruginosa Related to Specific Growth Rate: Insight into the Effects of Abiotic Factors. Inland Waters, 4, 357-362.
http://dx.doi.org/10.5268/IW-4.4.710 - 14. Daley, S.M.E., Kappell, A.D., Carrick, M.J. and Burnap, R.L. (2012) Regulation of the Cyanobacterial CO2-Concen-trating Mechanism Involves Internal Sensing of NADP+ and α-Ketogutarate Levels by Transcription Factor CcmR. PLoS ONE, 7, e41286.
http://dx.doi.org/10.1371/journal.pone.0041286 - 15. Sandrini, G., Matthijs, H.C.P., Verspagen, J.M.H., Muyzer, G. and Huisman, J. (2014) Genetic Diversity of Inorganic Carbon Uptake Systems Causes Variation in CO2 Response of the Cyanobacterium Microcystis. ISME Journal, 8, 589-600.
http://dx.doi.org/10.1038/ismej.2013.179 - 16. Song, Y. and Qiu, B. (2007) The CO2 Concentrating Mechanism in the Bloom-Forming Cyanobacterium Microcystis aeruginosa (Cyanophyceae) and Effects of UVB Radiation on Its Operation. Journal of Phycology, 43, 957-964.
http://dx.doi.org/10.1111/j.1529-8817.2007.00391.x - 17. Kehr, J.-C. and Dittmann, E. (2015) Biosynthesis and Function of Extracellular Glycans in Cyanobacteria. Life, 5, 164-180.
http://dx.doi.org/10.3390/life5010164 - 18. Yang, Z., Geng, L., Wang, W. and Zhang, J. (2012) Combined Effects of Temperature, Light Intensity, and Nitrogen Concentration on the Growth and Polysaccharide Content of Microcystis aeruginosa in Batch Culture. Biochemical Systematics and Ecology, 41, 130-135.
http://dx.doi.org/10.1016/j.bse.2011.12.015 - 19. Regel, R.H., Brookes, J.D., Ganf, G.G. and Griffiths, R.W. (2004) The Influence of Experimentally Generated Turbulence on the Mash01 Unicellular Microcystis aeruginosa Strain. Hydrobiologia, 517, 107-120.
http://dx.doi.org/10.1023/B:HYDR.0000027341.08433.32 - 20. Hondzo, M. and Warnaars, T.A. (2008) Coupled Effects of Small-Scale Turbulence and Phytoplankton Biomass in a Small Stratified Lake. Journal of Environmental Engineering, 134, 954-960.
http://dx.doi.org/10.1061/(ASCE)0733-9372(2008)134:12(954) - 21. Chengala, A., Hondzo, M. and Mashek, D.G. (2013) Fluid Motion Mediates Biochemical Composition and Physiological Aspects in the Green Alga Dunaliella primolecta Butcher. Limnology and Oceanography: Fluids and Environments, 3, 74-88.
http://dx.doi.org/10.1215/21573689-2326826 - 22. Kenis, P.R. and Hoyt, J.W. (1971) Friction Reduction by Algal and Bacterial Polymers. Naval Undersea Research and Development Center, San Diego, No. NUC-TP-240.
- 23. Jenkinson, I.R. and Sun, J. (2014) Drag Increase and Drag Reduction Found in Phytoplankton and Bacterial Cultures in Laminar Flow: Are Cell Surfaces and EPS Producing Rheological Thickening and a Lotus-Leaf Effect? Deep Sea Research Part II: Topical Studies in Oceanography, 101, 216-230.
http://dx.doi.org/10.1016/j.dsr2.2013.05.028 - 24. Qiu, B. and Gao, K. (2002) Effects of CO2 Enrichment on the Bloom-Forming Cyanobacterium. Microcystis aeruginosa (Cyanophyceae): Physiological Responses and Relationships with the Availability of Dissolved Inorganic Carbon1. Journal of Phycology, 38, 721-729.
http://dx.doi.org/10.1046/j.1529-8817.2002.01180.x - 25. Abeliovich, A. and Shilo, M. (1972) Photooxidative Death in Blue-Green Algae. Journal of Bacteriology, 111, 682- 689.
- 26. Eloff, J.N., Steinitz, Y. and Shilo, M. (1976) Photooxidation of Cyanobacteria in Natural Conditions. Applied and Environmental Microbiology, 31, 119-126.
- 27. Jiménez, J. (1997) Ocean Turbulence at Millimeter Scales. Scientia Marina, 61, 47-56.
- 28. Guala, M., Liberzon, A., Tsinober, A. and Kinzelbach, W. (2007) An Experimental Investigation on Lagrangian Correlations of Small-Scale Turbulence at Low Reynolds Number. Journal of Fluid Mechanics, 574, 405-427.
http://dx.doi.org/10.1017/S0022112006004204 - 29. Doron, P., Bertuccioli, L., Katz, J. and Osborn, T.R. (2001) Turbulence Characteristics and Dissipation Estimates in the Coastal Ocean Bottom Boundary Layer from PIV Data. Journal of Physical Oceanography, 31, 2108-2134.
http://dx.doi.org/10.1175/1520-0485(2001)031<2108:TCADEI>2.0.CO;2 - 30. O’Connor, B.L. and Hondzo, M. (2008) Dissolved Oxygen Transfer to Sediments by Sweep and Eject Motions in Aquatic Environments. Limnology and Oceanography, 53, 566-578.
http://dx.doi.org/10.4319/lo.2008.53.2.0566 - 31. Dvoretsky, D., Dvoretsky, S., Peshkova, E. and Temnov, M. (2015) Optimization of the Process of Cultivation of Microalgae Chlorella Vulgaris Biomass with High Lipid Content for Biofuel Production. Chemical Engineering Transactions, 43, 361-366.
- 32. Kingsland, S.E. (1995) Modeling Nature: Episodes in the History of Population Ecology. University of Chicago Press, Chicago.
- 33. Badger, M.R., Palmqvist, K. and Yu, J.W. (1994) Measurement of CO2 and Fluxes in Cyanobacteria and Microalgae during Steady-State Photosynthesis. Physiologia Plantarum, 90, 529-536.
http://dx.doi.org/10.1111/j.1399-3054.1994.tb08811.x - 34. Brezonik, P.L. and Arnold, W.A. (2011) Water Chemistry: An Introduction to the Chemistry of Natural and Engineered Aquatic Systems. Oxford University Press, New York.
- 35. Crayton, M.A. (1993) Toxic Cyanobacteria Blooms: A Field/Laboratory Guide. Office of Environmental Health Assessments, Washington State Department of Health, Olympia.
- 36. Thomas, W.H. and Gibson, C.H. (1990) Effects of Small-Scale Turbulence on Microalgae. Journal of Applied Phycology, 2, 71-77.
http://dx.doi.org/10.1007/BF02179771 - 37. Fraisse, S., Bormans, M. and Lagadeuc, Y. (2015) Turbulence Effects on Phytoplankton Morphofunctional Traits Selection: Functional Traits Selected by Turbulence. Limnology and Oceanography, 60, 872-884.
http://dx.doi.org/10.1002/lno.10066 - 38. Yang, Z., Kong, F., Shi, X., Yu, Y. and Zhang, M. (2014) UV-B Radiation and Phosphorus Limitation Interact to Affect the Growth, Pigment Content, and Photosynthesis of the Toxic Cyanobacterium. Microcystis aeruginosa. Journal of Applied Phycology, 26, 1669-1674.
http://dx.doi.org/10.1007/s10811-013-0225-y - 39. Chen, L., Mao, F., Kirumba, G.C., Jiang, C., Manefield, M. and He, Y. (2015) Changes in Metabolites, Antioxidant system, and Gene Expression in Microcystis aeruginosa under Sodium Chloride Stress. Ecotoxicology and Environmental Safety, 122, 126-135.
http://dx.doi.org/10.1016/j.ecoenv.2015.07.011 - 40. Gasljevic, K., Hall, K., Chapman, D. and Matthys, E.F. (2008) Drag-Reducing Polysaccharides from Marine Microalgae: Species Productivity and Drag Reduction Effectiveness. Journal of Applied Phycology, 20, 299-310.
http://dx.doi.org/10.1007/s10811-007-9250-z - 41. Xu, H., Cai, H., Yu, G. and Jiang, H. (2013) Insights into Extracellular Polymeric Substances of Cyanobacterium. Microcystis aeruginosa Using Fractionation Procedure and Parallel Factor Analysis. Water Research, 47, 2005-2014.
http://dx.doi.org/10.1016/j.watres.2013.01.019 - 42. Saddoughi, S.G. and Veeravalli, S.V. (1994) Local Isotropy in Turbulent Boundary Layers at High Reynolds Number. Journal of Fluid Mechanics, 268, 333-372.
http://dx.doi.org/10.1017/S0022112094001370
Appendix
A.1. Lake Minnetonka Data
Data were collected in August 2014 in Lake Minnetonka, MN from Halsted Bay, a site frequently reported to have HAB activity. The field measurements were performed using a SondTek MicroADV (acoustic-Doppler velocimetry) (SondTek, San Diego, CA, USA) to measure u, v, and w velocity time series at 50 Hz acquisition, and Hydrolab 4a Datasonde (Hach Company, Ames, IA, USA) to measure: temperature, pH, DO, specific conductivity, depth and PAR at full depth.
A.2. Velocity Analysis
The ADV velocity data were taken within the photic zone at a 0.67 m depth, and were process by Win ADV software (US Department of Interior Bureau of Reclamation). As shown in Table 1, the averaged pH, DO and light (PAR) at 0.67 m depth are consistent with the initial conditions established in the laboratory speaker reactor experiments.
A.3. Energy Dissipation Rate Estimation
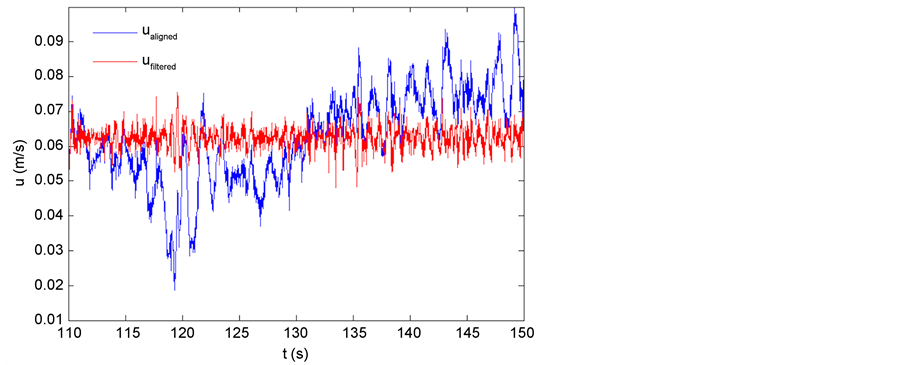
The energy dissipation rate, ε, for the field data can be estimated by using the velocity time series from the ADV (see Figure A1) and the second order structure function (see Figure A2). First, velocity (u) data was aligned to
Figure A1. ualigned (m/s) compared to ufiltered (m/s).
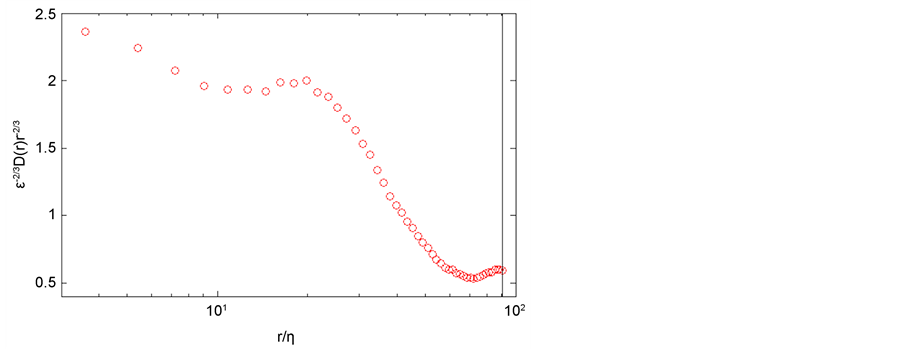
Figure A2. Normalized second order structure function of the ufiltered, the vertical black line represents the rcut = <u>/fcut.
the mean flow direction, ualigned. Then the ualigned time series was filtered (ufiltered) to remove the effect of surface waves using a high pass filter with a cut off frequency (fcut) of 1Hz.
We estimated the energy dissipation rate using the pre-multiplied second order structure function of ufiltered in the inertial range [42] :
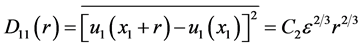
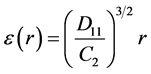
where C2 = 2.
In Figure A2, the spatial lag, r, is obtained by converting the times series, reported in Figure A1, using the mean velocity, <u>= 0.0625 m/s. The energy dissipation rate, reported in Table 2, is estimated by the plateau of the pre-multiplied second order structure function for r/η < 20 (Figure A2).