Received 5 June 2015; accepted 23 August 2015; published 26 August 2015

ABSTRACT

All tight monomials in quantum group for type A₅ with t ≤ 6 are determined in this paper.

Keywords:

Quantum Group, Canonical Basis, Tight Monomial

1. Introduction

The term “quantum groups” was popularized by V. G. Drinfel’d in his address to the International Congress of Mathematicians (ICM) in Berkeley (1986). However, quantum groups are actually not groups; they are nontrivial deformations of the universal enveloping algebras of semisimple Lie algebras, also called quantized enveloping algebras. These algebras were introduced independently by Drinfel’d [1] (in his definition, these algebras were infinitesimal, i.e., they were Hopf algebras over the field of formal power series) and Jimbo [2] (in his definition, these algebras were Hopf algebras over the field of rational functions in one variable) in 1985 in their study of exactly solvable models in the statistical mechanics. Quantum groups play an important role in the study of Lie groups, Lie algebras, algebraic groups, Hopf algebras, etc.; they are also closely linked with conformal field theory, quiver theory and knot theory.

The positive part of a quantum group has a kind of important basis, i.e., canonical basis introduced by Lusztig [3] , which plays an important role in the theory of quantum groups and their representations. However, it is difficult to determine the elements in canonical basis, which is interested in seeking the simplest elements in canonical basis, i.e., monomial basis elements. Some efforts have been done for monomial basis elements in quantum group of type A_n. Lusztig firstly introduced algebraic definition of canonical basis of quantum groups for the simply laced case (i.e., A_n, D_n, E_n), and gave explicitly the longest monomials for type A₁, A₂, which were all of canonical basis elements (see [3] ). Then, Lusztig [4] associated a quadratic form to every monomial. He showed that, given certain linear conditions, the monomial was tight, i.e., it belonged to canonical basis (respectively, semitight, i.e., it was a linear combination of elements in canonical basis with constant coefficients in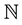) provided that the quadratic form satisfied a certain positivity condition (respectively, nonnegativity condition). He showed that the positivity condition (for tightness) always held in type A₃ and computed 8 longest tight monomials of type A₃. He also asked when we had (semi)tightness in type A_n. Based on Lusztig’s work, Xi [5] found explicitly all 14 canonical basis elements of type A₃ (consisting of 8 longest monomials and 6 polynomials with one-dimensional support). For type A₄, Hu, Ye and Yue [6] determined all 62 longest monomials in canonical basis, Hu and Ye [7] gave all 144 polynomials with one-dimensional support in canonical basis, and Li and Hu [8] got 112 polynomials with two-dimensional support in canonical basis. For type A_n (n ≥ 5), Marsh [9] carried out thorough investigation. He presented a semitight longest monomial for type A₅. However, he proved that a class of special longest monomials did not satisfy sufficient condition of tightness or semitightness for type A_n (n ≥ 6) (although it might turn out that the corresponding monomials were still tight). Reineke [10] associated a new quadratic form to every monomial, and gave a sufficient and necessary condition for the monomial to be tight for the simply laced case in terms of the quadratic form. By use of this criterion, Wang [11] listed all tight monomials for type A₃, in which 8 longest tight monomials were the same as Lusztig and Xi’s results.

Based on Reineke’s criterion and some other results, all tight monomials for type A₅ with t ≤ 6 are determined in this paper.

2. Preliminaries

Let be a Cartan matrix of finite type, be a diagonal matrix with integer en-

tries making the matrix DC symmetric. Let 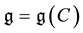be the complex semisimple Lie algebra associated with C, and let 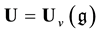(here v is an indeterminate) be the corresponding quantized enveloping algebra, whose positive part U⁺ is the 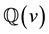-subalgebra of U generated by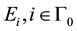, subject to the relations

,

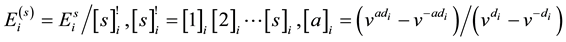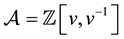where. Let, U⁺ be the

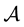
-subalgebra of U⁺ generated by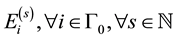. Corresponding to every reduced expression i of the longest element of the Weyl group of, one constructs a PBW basis B_i of U⁺. Lusztig proved that the 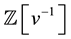-lattice 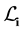spanned by B_i is independent of the choice of i, write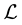; and the image of B_i in the -module is a basis B of independent of i. Let be the image of under the bar map of U⁺ de- fined by and. Canonical basis B is the preimage of B under -module isomorphism.

A monomial in U⁺ is an element of the form

(*)

where. When is the longest element of Weyl group, the monomial (*) is called the longest monomial. We say that (*) is tight if it belongs to B; we say that (*) is semitight if it is a linear combination of elements in B with constant coefficients.

Let be a finite quiver with vertex set Q₀ and arrow set Q₁. Write as, where h_ρ

and t_ρ denote the head and the tail of ρ respectively. An automorphism σ of Q is a permutation on the vertices of

Q and on the arrows of Q such that and for any. Denote the quiver with

automorphism σ as. Attach to the pair a valued quiver as follows. Its vertex set and arrow set are simply the sets of σ-orbits in Q₀ and Q₁, respectively. The valuation of

is given by,;,. The

Euler form of is defined to be the bilinear form given by

,

where, so is the symmetric Euler form. The valued quiver defines a Cartan matrix, where

Let t be a non-negative integer. Let and. We write

.

Define

where

Obviously,.

The following results are very useful in the determination of tight monomials.

Theorem 2.1 [4] (Lusztig, 1993). Let U be the quantum group of type, as before. If the following quadratic form takes only values < 0 on, then monomial is tight.

Theorem 2.2 [10] (Reineke, 2001). Let U be the quantum group of type A_n, D_n, E_n, as before, the monomial is tight if and only if the following quadratic form takes only values < 0 on

If are mutually different, then, by Theorem 2.2, we have the following Corollaries.

Corollary 2.3. When are mutually different, monomial is tight.

Corollary 2.4. If is tight, then for any mutually different

and any mutually different, and,

is also tight.

Theorem 2.5 [12] (Deng-Du, 2010). Let and. If is tight, then

(a) For, monomial is also tight;

(b) For,.

Theorem 2.6 [4] (Lusztig, 1993). Let be the non-trivial automorphism of U⁺ induced by Dynkin diagram

automorphism of, and be the unique -algebra isomorphism such that.

If is tight, then and are all tight.

3. Main Results

Let. For convenience, we abbreviate a monomial

as a word (1 as 0), an inequality as. For example,

a monomial is abbreviated to, a monomial to 1234, etc.

By Theorem 2.5(b), we only consider those words with in determining tight monomials, in this case, we call the word with t-value, the monomial with t-value. If for some, we identify the word with the word. Let us present the so called word-procedure for making the words with - value from the words with t-value. Let be a word with t-value, we firstly add a number different from i₁ (or i_t) in the front (or behind) of i₁ (or i_t), secondly delete the words with t-value, lastly apply the automorphism and isomorphism. After the above procedure put into practice for all the words with t-value, we get all words with -value by deleting repeated words. For example, by applying the above word-procedure to the word 13 with 2-value, we get the words with 3-value as follows: 132, 134, 135, 143, 213, 235, 325, 354, 435.

Theorem 3.1. Let M_t be the set of all tight monomials with t-value in quantum group for type A₅, we have the following results.

(1) t = 0, , tight monomial has only one;

(2) t = 1, if, then, tight monomials have 5 families;

(3) t = 2, if, then, tight monomials have 14 families;

(4) t = 3, if, where

, ,

then, tight monomials have 33 families;

(5) t = 4, if where

then, tight monomials have 67 families;

(6) t = 5, if where

then, tight monomials have 125 families;

(7) If t = 6, where

then, tight monomials have 222 families;

4. Proof of Theorem 3.1

Consider the quiver of type A₅, where,. Let

id be the identity automorphism of Q, then valued quiver of is. The valuation is given by . Euler form on is

,

Symmetric Euler form on is

,

where.

By simple computation, we have

, , and.

Let us prove Theorem 3.1.

Case 1.. By Corollary 2.3, monomials with are all tight.

Case 2. t = 3. Applying the word-procedure on S₂, we get 33 words with 3-value. By considering and, we get. By Corollary 2.3, monomials in are all tight. For, it suffices to consider. For any, we have, where

and

Obviously, if and only if. So monomial is tight by Theorem 2.2.

Case 3. t = 4. Applying the word-procedure on, we get 75 words with 4-value. By considering and, we get. When, for any, we have

,

where

and

Obviously, if and only if, this is a contradiction. Applying, one gets that the monomials corresponding to

are all not tight for any.

Monomials in are all tight by Corollary 2.3. By and Corollary 2.4, monomials in are all tight. For, it suffices to consider. For any, we have

,

where

and

if and only if. So is tight by Theorem 2.2.

Case 4. t = 5. Applying the word-procedure on, and deleting words including subwords 1212, 2121, 2323, 3232, 3434, 4343, 4545 and 5454 (considering Theorem 2.5(a)), we get 125 words with 5-value. By considering and, we get. By Corollary 2.3, monomials in are all tight. Monomials in are all tight by and Corollary 2.4. Monomials in are all tight by and Corollary 2.4.

For, it suffices to consider. For any, we have

,

where

and

if and only if. So

is tight by Theorem 2.2.

For, it suffices to consider. For any, we have

,

where

and

if and only if. So

is tight by Theorem 2.2.

For, it suffices to consider. For any, we have

,

where

and

if and only if. So

is tight by Theorem 2.2.

For, it suffices to consider. For any, we have

,

where

and

if and only if. So

is tight by Theorem 2.2.

Case 5. t = 6. Applying the word-procedure on S₅, and deleting words including subwords 1212, 2121, 2323, 3232, 3434, 4343, 4545 and 5454(considering Theorem 2.5(a)), we get 228 words with 6-value. By considering Φ and Ψ, we get. When, for any, we have

,

where

and

if and only if. This is a contradiction. Applying, one gets that the monomials corresponding to

are all not tight for any.

By Corollary 2.4, we have, , , , , , , and.

For, it suffices to consider. For any, we have

where

and

if and only if. So

is tight by Theorem 2.2.

For, it suffices to consider. For any, we have

where

and

if and only if. So

is tight by Theorem 2.2.

For, it suffices to consider. For any, we have

where

and

if and only if. So

is tight by Theorem 2.2.

For, it suffices to consider. For any, we have

where

and

if and only if. So

is tight by Theorem 2.2.

Funding

This paper is supported by the NSF of China (No. 11471333) and Basic and advanced technology research project of Henan Province (142300410449).

Cite this paper

YuwangHu,GuiweiLi,JunWang, (2015) Tight Monomials in Quantum Group for Type A₅ witht ≤ 6. Advances in Linear Algebra & Matrix Theory,05,63-75. doi: 10.4236/alamt.2015.53007

References

NOTES

^*Corresponding author.