ABSTRACT

Let 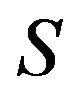be a nonempty, proper subset of all refined inertias. Then, 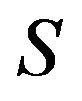is called a critical set of refined inertias for ireducible sign patterns of order 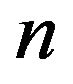if is sufficient for any sign pattern to be refined inertially arbitrary. If no proper subset of 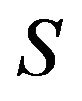is a critical set of refined inertias, then 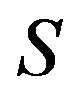is a minimal critical set of refined inertias for sign patterns of order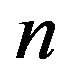. In this paper, all minimal critical sets of refined inertias for irreducible sign patterns of order 2 are identified. As a by-product, a new approach is presented to identify all minimal critical sets of inertias for irreducible sign patterns of order 2.

1. Introduction

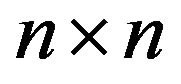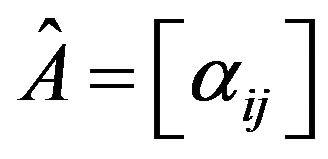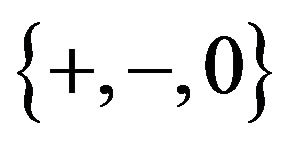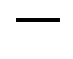A sign pattern is a matrix with entries from the set where (respectively,) denotes a positive (respectively, negative) real number; see, e.g., [1]. The set of all real matrices with the same sign pattern as the sign pattern is the qualitative class

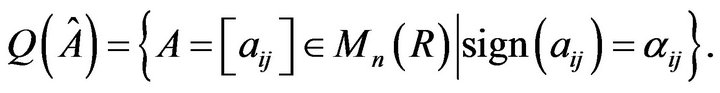
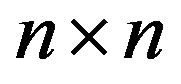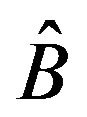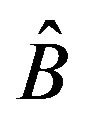A subpattern of an sign pattern is a sign pattern obtained by replacing some (possibly empty) subset of the nonzero entries of with zeros. If is a subpattern of, then is a superpattern of. Two square zero-nonzero patterns and 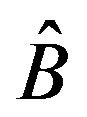are equivalent if one can be obtained from the other by any combination of transposition and permutation similarity. A sign pattern is reducible if it is permutation similar to a pattern of the form

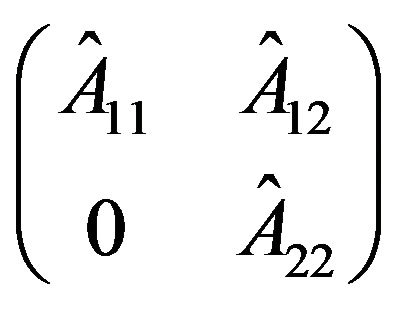
where 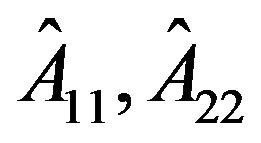are square and non-vacuous. A pattern is irreducible if it is not reducible.

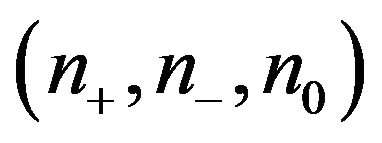The inertia of a matrix is an ordered triple where 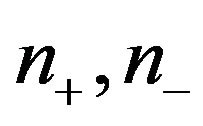and 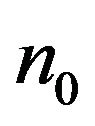are the number of eigenvalues of with positive, negative and zero real part, respectively; see, e.g., [2]. The refined inertia of is the ordered quadruple 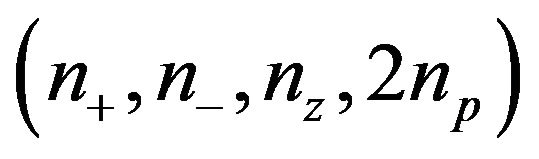of nonnegative integers that sum to, where is the inertia of while 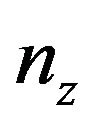is the number of 0 as an eigenvalue of and 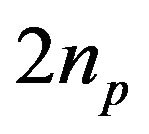is the number of eigenvalues of with nonzero pure imaginary eigenvalues; see, e.g., [3]. The inertia (respectively, refined inertia) of a sign pattern is 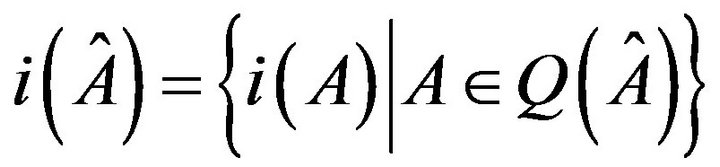(respectively,

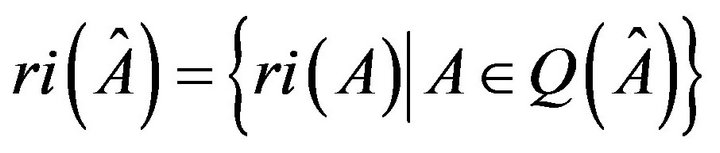). A sign pattern

is an inertially arbitrary pattern (IAP) if given any ordered triple 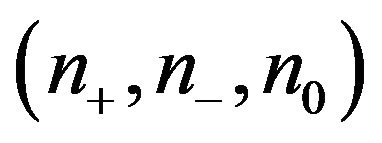of nonnegative integers with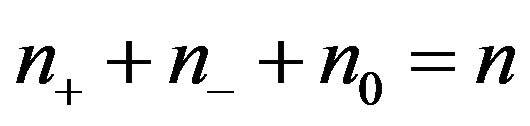, there exists a real matrix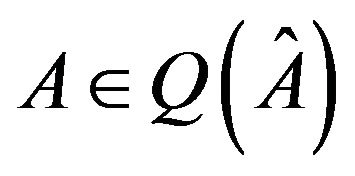

such that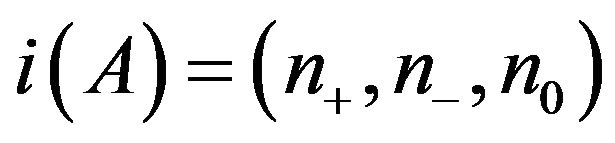; see, e.g., [4,5] and the reference therein. Similarly, is a refined inertially arbitrary pattern (rIAP) if given any ordered quadruple 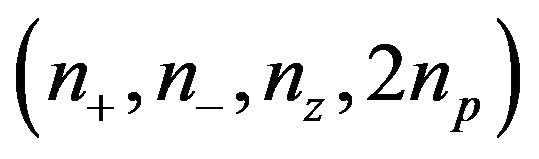of nonnegative integers that sum to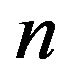, there exists a real matrix 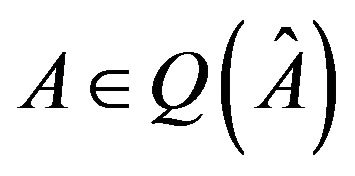such that 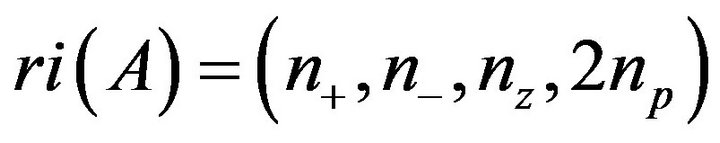; see, e.g., [3].

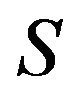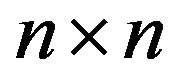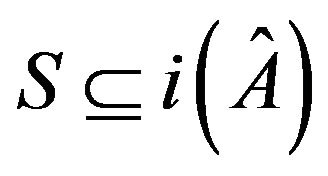Let be a nonempty, proper subset of the set of all inertias for any zero-nonzero (or sign) pattern. If is sufficient for to be inertially arbitrary, then 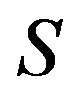is said to be a critical set of inertias for zero-nonzero (or sign) patterns of order 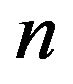and if no proper subset of 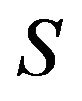is a critical set of inertias, then 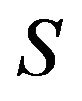is said to be a minimal critical set of inertias for zerononzero (or sign) patterns of order; see, e.g., [6]. Critical sets of refined inertias for irreducible zero-nonzero patterns are defined in [7]. Similarly, we introduce the concept of a critical set of refined inertias for sign patterns. Let 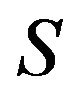be a nonempty, proper subset of all refined inertias. Then, 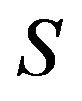is called a critical set of refined inertias for sign patterns of order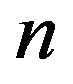, if the set 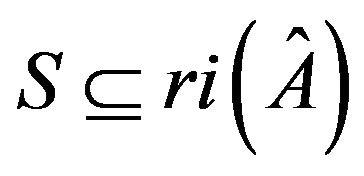is sufficient for any sign pattern to be refined inertially arbitrary. If no proper subset of 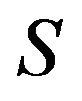is a critical set of refined inertias, then 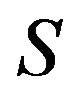is a minimal critical set of refined inertias for irreducible sign patterns of order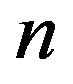. We note that all minimal critical sets of inertias for irreducible sign patterns of order 2 have been identified in [6]. But, identifying all minimal critical sets of inertias for irreducible zero-nonzero (or sign) patterns of order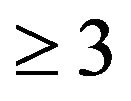has been posed as an open question in [6]. Also open is the minimum cardinality of such a set. The concept of critical sets of refined inertias for sign pattern is introduced for the first time. In this work, we concentrate on the minimal critical sets of refined inertias for irreducible sign patterns of order 2.

Our work is organized as follows. Section 2 describes some preliminary results on the refined inertias of sign patterns. The minimal critical sets of refined inertias for irreducible sign patterns of order 2 are identified in Section 3. In Section 4, as a by-product, an alternative proof is given to identify all minimal critical sets of inertias for 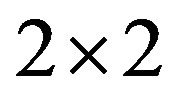irreducible sign patterns. Some concluding remarks are given in Section 5.

2. Preliminaries

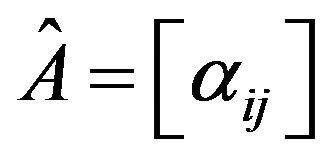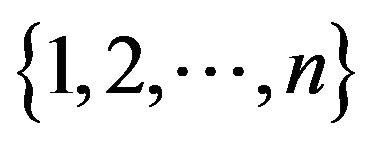Recall that a sign pattern has its associated digraph with vertex set and for all 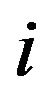and, a positive (resp., negative ) arc from 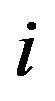to if and only if 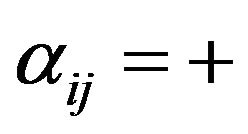(resp.,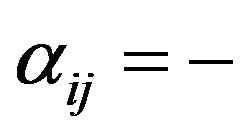). A (directed) simple cycle (or a k-cycle) 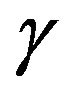of length k is a sequence of k arcs 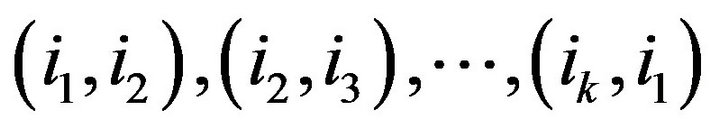such that these vertices are distinct; see, e.g., [1]. The sign positive (or negative) of a simple cycle in a sign pattern is the actual product of the entries in the cycle, following the obvious rules that multiplication is commutative and associative, and (+)(+) = +,(+)(−) = −.

Lemma 2.1. let be an irreducible sign pattern of order 2. Then the following are equivalent:

(1) is spectrally arbitrary;

(2) is inertially arbitrary;

(3) Up to equivalence,;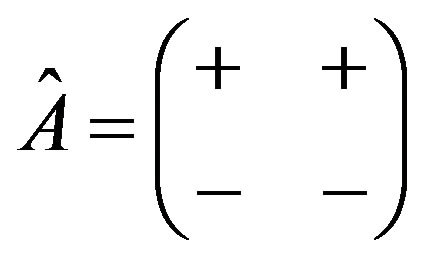

(4) Associated digraph of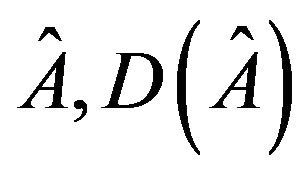, has two loops of opposite sign and a negative 2-cycle.

Proof. The equivalences of 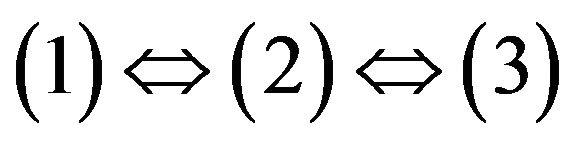follow from Proposition 3 in [6]. The equivalence of 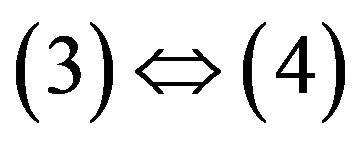can be verified directly.

It is known that there are seven refined inertias for 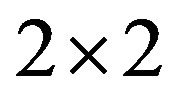sign patterns. To identify all minimal critical sets of refined inertias for irreducible sign patterns of order 2, the following three sign patterns are necessary to be investigated.

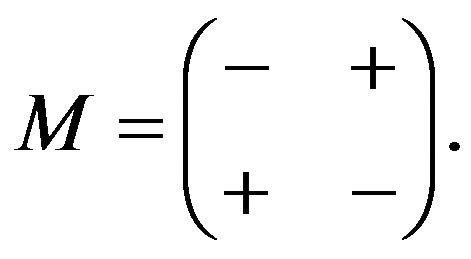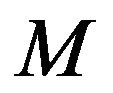Lemma 2.2. Let Then, allows the only refined inertias (0, 1, 1, 0), (0, 2, 0, 0) and (1, 1, 0, 0).

Proof. Since 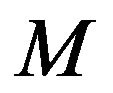requires every realization with a negative trace, the refined inertias (2, 0, 0, 0), (0, 0, 2, 0), (0, 0, 0, 2) and (1, 0, 1, 0) cannot be allowed by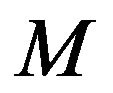. For the remaining refined inertias, consider realizations of

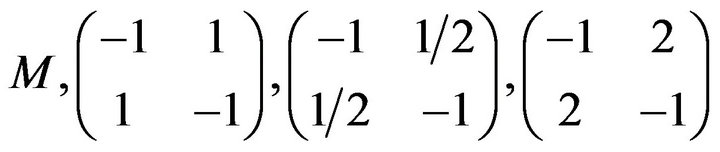with refined inertias (0, 1, 1, 0), (0, 2, 0, 0) and (1, 1, 0, 0), respectively. It follows that allows the only refined inertias (0, 1, 1, 0), (0, 2, 0, 0), (1, 1, 0, 0).

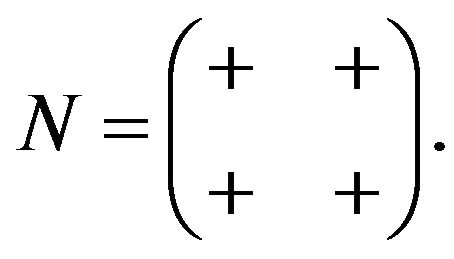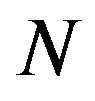Lemma 2.3. Let Then, allows all refined inertias except (0, 1, 1, 0), (0, 2, 0, 0), (0, 0, 2, 0) and (0, 0, 0, 2).

Proof. Since 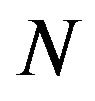requires every realization with a positive trace, the refined inertias (0, 1, 1, 0), (0, 2, 0, 0), (0, 0, 2, 0) and (0, 0, 0, 2) cannot be allowed by. Consider the following realizations of,

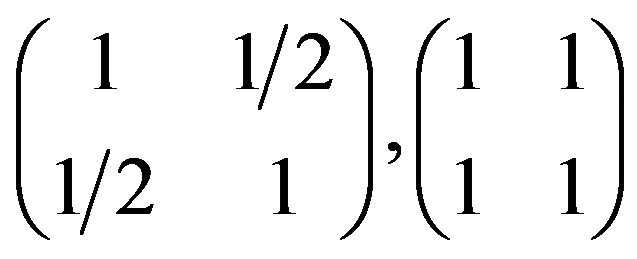and 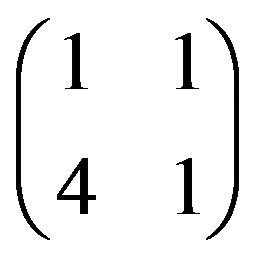with refined inertias (20, 0, 0), (1, 0, 1, 0) and (1, 1, 0, 0), respectively. It follows that allows all refined inertias except (0, 1, 1, 0), (0, 2, 0, 0), (0, 0, 2, 0) and (0, 0, 0, 2).

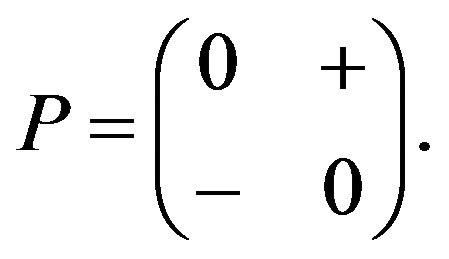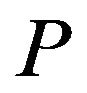Lemma 2.4. Let Then, allows the refined inertia (0, 0, 0, 2).

Proof. Lemma 2.4 follows from the fact that a realization of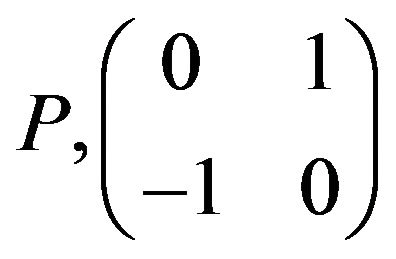, has (0, 0, 0, 2) as its refined inertia.

3. Minimal Critical Sets of Refined Inertias for Irreducible Sign Patterns of Order 2

We are now to identify all minimal critical sets of refined inertias for irreducible sign patterns of order 2.

Theorem 3.1. The set {(0, 0, 2, 0)} is the only minimal critical set with a single refined inertia for 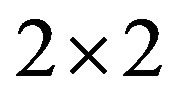ireducible sign patterns.

Proof. Lemma 2.2 indicates that {(0, 2, 0, 0), {(1, 1, 0, 0)} and {(0, 1, 1, 0)} cannot be a minimal critical set of refined inertias. Lemma 2.3 indicates that {(2, 0, 0, 0)} and {(1, 0, 1, 0)} cannot be a minimal critical set of refined inertias. Lemma 2.4 indicates that {(0, 0, 0, 2)} cannot be a minimal critical set of refined inertias. So, it suffices to show that the set {(0, 0, 2, 0)} is a minimal critical sets of refined inertias.

If {(0, 0, 2, 0)} is allowed by an arbitrary irreducible sign pattern of order 2, then all the main diagonal entries of must be nonzero. Since allows a realization with a zero trace, the two diagonal entries of are of opposite sign. That is to say, the associated digraph of, has a positive loop and a negative loop. For allows a realization with zero determinant, has a negative 2-cycle. It follows from Lemma 2.1 that is refined inertially arbitrary.

Theorem 3.2. The refined inertia sets {(0, 0, 0, 2), (1, 0, 1, 0)}, {(0, 0, 0, 2), (0, 1, 1, 0)}, {(0, 0, 0, 2), (2, 0, 0, 0)}, {(0, 0, 0, 2), (0, 2, 0, 0)}, {(0, 0, 0, 2), (1, 1, 0, 0)}, {(1, 0, 1, 0), (0, 1, 1, 0)}, {(1, 0, 1, 0), (0, 2, 0, 0)}, {(1, 0, 1, 0), (2, 0, 0, 0)} and {(2, 0, 0, 0), (0, 2, 0, 0)} are minimal critical sets of refined inertias for irreducible sign patterns of order 2.

Proof. Let be an arbitrary irreducible sign pattern of order 2. If {(0, 0, 0, 2), (1, 0, 1, 0)}, then allows a realization with a positive trace and a realization with zero trace. It follows that 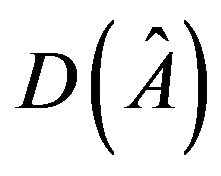has a positive loop and a negative loop. Since allows a realization with zero determinant, 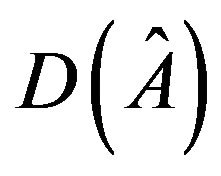has a negative 2-cycle. By Lemma 2.1, is refined inertially arbitrary and {(0, 0, 0, 2), (1, 0, 1, 0)} is a minimal critical set of refined inertias for 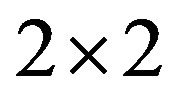irreducible sign patterns. Similarly, we can show the refined inertias {(0, 0, 0, 2), (0, 1, 0)}, {(0, 0, 0, 2), (2, 0, 0, 0)}, {(0, 0, 0, 2), (0, 2, 0, 0)}, {(1, 0, 1, 0), (0, 1, 1, 0)}, {(1, 0, 1, 0), (0, 2, 0, 0)}, {(1, 0, 1, 0), (2, 0, 0, 0)} and {(2, 0, 0, 0), (0, 2, 0, 0)} are minimal critical sets of refined inertias for irreducible sign patterns.

For the refined inertia set {(0, 0, 0, 2), (1, 1, 0, 0)}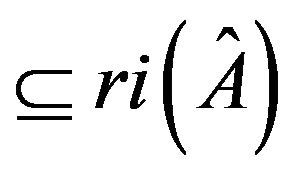, we claim that the diagonal entries of must be nonzero. In fact, assume that there exists at least a zero diagonal entry of. Then sign pattern requires nonsingularity. It is contradicted that allows two realizations with a positive and negative determinant, respectively. So, the diagonal entries of must be nonzero. And the fact that the diagonal entries of are of opposite sign follows from that allows a realization with a zero trace. 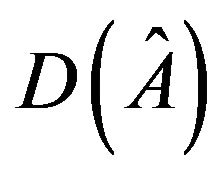has a negative simple cycle of length 2 follows from that the inertia (0, 0, 0, 2).

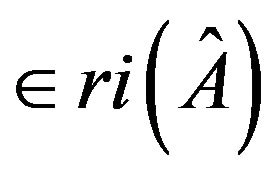Next we identify all minimal critical sets of refined inertias for 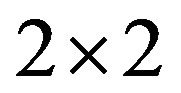irreducible sign patterns.

Theorem 3.3. The sets {(0, 0, 2, 0)}, {(0, 0, 0, 2), (1, 0, 1, 0)}, {(0, 0, 0, 2), (0, 1, 1, 0)}, {(0, 0, 0, 2), (2, 0, 0, 0)}, {(0, 0, 0, 2), (0, 2, 0, 0)}, {(0, 0, 0, 2), (1, 1, 0, 0)}, {(1, 0, 1, 0), (0, 1, 1, 0)}, {(1, 0, 1, 0), (0, 2, 0, 0)}, {(1, 0, 1, 0), (2, 0, 0, 0)} and {(2, 0, 0, 0), (0, 2, 0, 0)} are the only minimal critical sets of refined inertias for irreducible sign patterns.

Proof. By Theorems 3.1 and 3.2, the refined inertia sets stated in Theorem 3.3 are minimal critical sets of refined inertias for 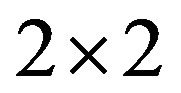irreducible sign patterns. To show there exists no other minimal critical sets of refined inertias, it suffices to show that the remaining nine refined inertia sets with cardinality 2, {(1, 0, 1, 0), (2, 0, 0, 0)}, {(1, 0, 1, 0), (1, 1, 0, 0)}, {(2, 0, 0, 0), (1, 1, 0, 0)}, {(0, 1, 1, 0), (0, 2, 0, 0)}, {(0, 1, 1, 0), (1, 1, 0, 0)}, {(1, 1, 0, 0), (0, 2, 0, 0)} and the two refined inertia sets with cardinality 3, {(1, 0, 1, 0), (2, 0, 0, 0), (1, 1, 0, 0)} and {(0, 1, 1, 0), (0, 2, 0, 0), (1, 1, 0, 0)} are not critical sets of refined inertias. By Lemma 2.3, {(1, 0, 1, 0), (2, 0, 0, 0)}, {(1, 0, 1, 0), (1, 1, 0, 0)}, {(2, 0, 0, 0), (1, 1, 0, 0)} and {(1, 0, 1, 0), (2, 0, 0, 0)}, (1, 1, 0, 0)} are not critical sets of refined inertias. By Lemma 2.2, {(0, 1, 1, 0), (0, 2, 0, 0)}, {(0, 1, 1, 0), (1, 1, 0, 0)}, {(1, 1, 0, 0), (0, 2, 0, 0)} and {(0, 1, 1, 0), (0, 2, 0, 0)}, (1, 1, 0, 0)} are not critical sets of refined inertias.

The following theorem follows directly for Theorem 3.3.

Theorem 3.4. Let be a irreducible sign pattern of order 2. Then the following are equivalent:

1) is refined inertially arbitrary;

2) allows (0, 0, 2, 0);

3) allows (0, 0, 0, 2) and (1, 0, 1, 0);

4) allows (0, 0, 0, 2) and (0, 1, 1, 0);

5) allows (0, 0, 0, 2) and (2, 0, 0, 0);

6) allows (0, 0, 0, 2) and (0, 2, 0, 0);

7) allows (0, 0, 0, 2) and (1, 1, 0, 0);

8) allows (1, 0, 1, 0) and (0, 1, 1, 0);

9) allows (1, 0, 1, 0) and (0, 2, 0, 0);

10) allows (1, 0, 1, 0) and (2, 0, 0, 0);

11) allows (2, 0, 0, 0) and (0, 2, 0, 0).

4. Minimal Critical Sets of Inertias for Irreducible Sign Patterns of Order 2

In [6], all minimal critical sets of inertias for 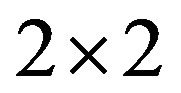irreducible sign patterns, which are restated here as Theorem 4.1, have been identified. In this section, we present an alternative proof in terms of critial sets of refined inertias, as a by-product.

Theorem 4.1. The sets {(2, 0, 0), (0, 0, 2)}, {(0, 2, 0), (0, 0, 2)}, {(2, 0, 0), (0, 1, 1)}, {(0, 2, 0), (1, 0, 1)}, {(1, 1, 0), (0, 0, 2)}, {(1, 0, 1), (0, 0, 2)}, {(0, 1, 1), (0, 0, 2)}, {(2, 0, 0), (0, 2, 0)} and {(1, 0, 1), (0, 1, 1)} are the only minimal critical sets of inertias for 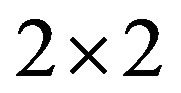irreducible sign patterns.

Proof. Note that an irreducible 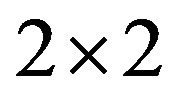sign pattern:

allows {(0, 0, 2), (2, 0, 0)} if and only if it allows

{(2, 0, 0, 0), (0, 0, 2, 0)} or {(2, 0, 0, 0), (0, 0, 0, 2)}allows {(0, 0, 2), (0, 2, 0)} if and only if it allows

{(0, 2, 0, 0), (0, 0, 2, 0)} or {(0, 2, 0, 0), (0, 0, 0, 2)}allows {(2, 0, 0), (0, 1, 1)} if and only if it allows

{(2, 0, 0, 0), (0, 1, 1, 0)}allows {(0, 2, 0), (1, 0, 1)} if and only if it allows

{(0, 2, 0, 0), (1, 0, 1, 0)}allows {(1, 1, 0), (0, 0, 2)} if and only if it allows

{(0, 0, 0, 2), (1, 1, 0, 0)} or {(0, 0, 2, 0), (1, 1, 0, 0)}allows {(1, 0, 1), (0, 0, 2)} if and only if it allows

{(0, 0, 0, 2), (1, 0, 1, 0)} or {(0, 0, 2, 0), (1, 0, 1, 0)}allows {(0, 1, 1), (0, 0, 2)} if and only if it allows

{(0, 0, 0, 2), (0, 1, 1, 0)} or {(0, 0, 2, 0), (0, 1, 1, 0)}allows {(2, 0, 0), (0, 2, 0)} if and only if it allows

{(2, 0, 0, 0), (0, 2, 0, 0)}allows {(1, 0, 1), (0, 1, 1)} if and only if it allows

{(0, 1, 1, 0), (1, 0, 1, 0)}.

Since all of the refined inertia sets above are critical sets of refined inertias (not necessarily minimal), the above sets of inertias are critical sets, and indeed are also easily seen to be minimal (since at least one of the corresponding sets of refined inertias is minimal in each case). It follows that the above sets of inertias are the only minimal critical sets of inertias because the corresponding sets of refined inertias are the only minimal critical sets of refined inertias.

5. Concluding Remarks

We have identified all minimal critical sets of refined inertias for irreducible sign patterns of order 2. As a by-product, all minimal critical sets of inertias for irreducible sign patterns of order 2 have also been identified in a new proof. In a follow-up paper, we will consider other cases, e.g., 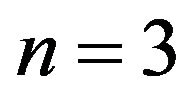, though identification of all critical sets of inertias for irreducible sign patterns of order 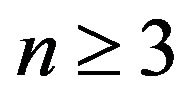has been posed as an open question in [6].

6. Acknowledgements

The authors would like to express their great gratitude to the referees and editor for their constructive comments and suggestions that led to the enhancement of this paper. This research was supported in part by the Sci. & Tech. Research Fund of Huaiyin Institute of Technology (HGB1111), National Natural Science Foundation of China (11201168) and Natural Science Foundation of the Higher Education Institutions of Jiangsu Province (Grant No. 12KJB110001).

REFERENCES